适用于CEI的GEO卫星相时延解算方法及试验
黄 磊,刘友永,陈少伍,孟 玮,李海涛
(1. 北京跟踪与通信技术研究所,北京 100094;2. 中国电子科技集团公司第五十四研究所,石家庄 050081)
(circle) and residual phase delay (dot))
(circle) and residual phase delay (dot))
0 引 言
干涉测量技术作为一种高精度测角手段,对航天器横向的位置和速度有较好的约束,通过与测距、测速等外测数据相结合,可有效提高定轨精度[1]。按照基线的长短,干涉测量可分为甚长基线干涉测量(Very long baseline interferomety,VLBI)和连线干涉测量(Connected element interferometry,CEI)两大类。其中VLBI的基线长达数千公里,通过群时延测量即可实现高精度测角,通常应用于深空探测器导航[2]。CEI技术基线一般为几十公里,它通过对载波相时延测量,进而实时获得目标相对于基线矢量的精确角位置。可适用于中高轨卫星的高精度测定轨及相对定位,其面临的技术难题是单基线情况下载波相位整周期模糊度解算问题。
美国NASA自20世纪80年代末就开始进行CEI技术研究和试验验证,并针对载波相位解模糊问题提出了多基线相位参考、频率综合和地球自转综合3种方法[3-6],其中,多基线相位参考法的核心思想是利用长短不等的多条基线按照射电天文成图的方法综合求解相位模糊[6-8],缺点是需要大规模的天线阵列,造价昂贵;频率综合法的核心思想是利用很宽的扩展带宽获得群时延,再进一步确定载波的相位延迟整周模糊,以日本SELENE任务为代表[9-10],缺点是必须开展专门的星上频率信标设计,不具备普适性;地球自转综合法的核心思想是利用地球自转的特点,长时间连续测量获得不同方向基线变化进行解模糊[11],不适用于高轨卫星定轨场合。
美国曾在2002年利用图森和凤凰城两座城市之间的180 km基线对国际海事通信GEO卫星AOR-W开展了S频段CEI试验,定轨精度仅为3 km[12]。可以分析出,试验中利用的是卫星下行的群时延测控信号,未能获得无模糊载波相时延。
国内信息工程大学、北京宇航动力实验室等院校及科研机构对CEI技术进行了研究[13-17],论证了该技术的有效性和应用前景。但从文章发表情况来看,理论仿真的工作居多[13-15],或是仅评估了相时延观测量随机误差精度[16],未能得到精准的相时延观测量。文献[17]为2019年国内最新研究成果,采用了75 m和35 m的超短基线,对C频段GEO卫星最终定轨精度为1~2 km。由于基线极短且先验轨道的精度足够,不存在解载波相位模糊的问题,也未能体现出干涉测量高精度的测角优势。
为解决CEI技术在高轨卫星高精度测定轨面临了载波相位解模糊难题,本文创造性地提出了一种基于卫星遥测或数传等下行信号的多弧段融合相位模糊度解算方法,它通过相邻多弧段载波相位值和窄带信号群时延值的融合处理可精确获得无模糊载波相时延观测量,不需要大规模天线阵列和特殊的卫星下行信号,具有较好的应用前景。
为验证这一方法的有效性,利用我国航天测控网喀什地区的两个测控站为基础,补充光纤时频传递、数据采集记录、数据相关处理等设备,构建试验系统并进行了试验验证。试验采用某北斗GEO卫星(以下简称BD卫星)作为标校源,对某天链卫星(以下简称TL卫星)进行测量,采用交替观测模式(两颗卫星角距在10°以内)。通过TL卫星精轨对测量结果进行评估,结果表明:在20 km基线上,利用BD卫星的伪码测距信号和TL卫星的测控信号均成功实现了S频段解载波整周相位模糊,相时延测量精度能够达到0.1 ns,对应GEO卫星定轨精度优于54 m。研究成果已经应用于高分专项地面测控系统建设中。
1 CEI基础理论
1.1 CEI基本原理
CEI基本原理与在航天领域广泛应用的甚长基线干涉测量(VLBI)基本原理相一致。图1是干涉测量基本原理图[2],同样适用于CEI测量。
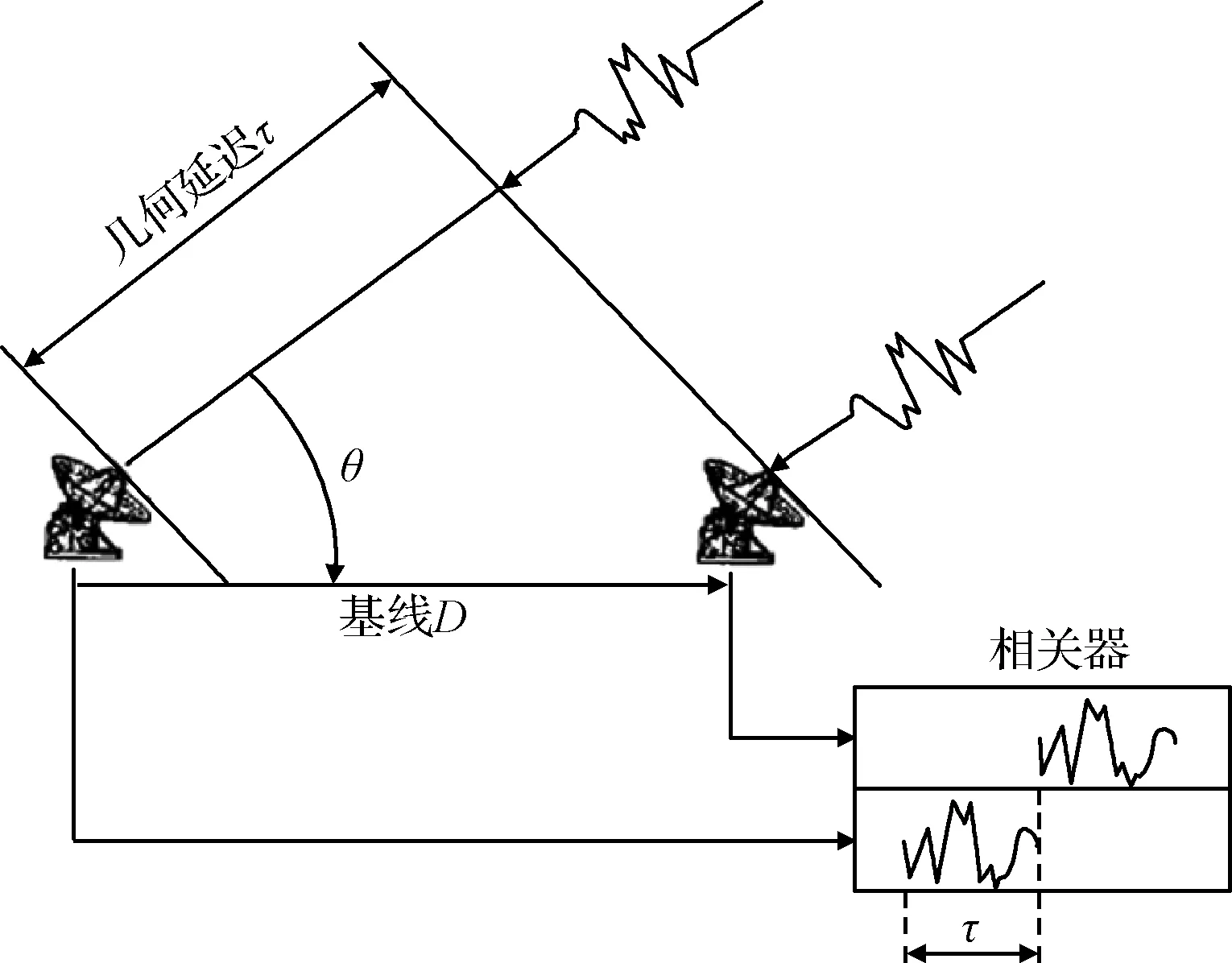
图1 干涉测量基本原理图
在图1中,干涉测量相关器处理的信号来自几何上分离的两个地面测站。从第一个测站到第二个测站的矢量D称作基线矢量。如果一个外部射电源其方向矢量为s,与基线矢量的夹角为θ,那么可以得到无线电信号源发出的信号波前到达基线两端的时间差近似为:
(1)
根据式(1),在基线D确定的条件下,由τg测量误差导致的θ测角误差可由式(2)表示:
(2)
可见,测角误差δθ与基线D的长度成反比,与τg的测量误差δτg成正比。因此,若要获得高精度角度测量,可以通过使用更长的基线(即增加D的长度)或提高干涉测量时延的测量精度,这也就是VLBI和CEI高精度测量技术的基本机理。
对于VLBI测量,由于两站相距甚远,无法采用相同的基准频率源,且通过双差分依然难以完全消除电离层和对流层的介质误差,因而难以实现目标的载波相时延测量,这是由于各种误差源的影响会最终引入到相时延观测量中,带来整周模糊,导致无法正确解算载波相位整周数,因此VLBI技术均采用群延迟测量体制。
对于CEI测量,虽然基线长度较短,但通过高精度的时间频率传递可以使得各测站采用相同的基准频率源,此外,由于两站之间距离较近,通过双差分能够基本完全消除电离层和对流层的介质误差[4],这为获得目标的载波相时延观测量奠定了基础。相时延的精度主要取决于射频信号的频率(一般为GHz量级),群时延的精度主要取决于两信标频率之差,通常是DOR音(对于S频段约为8 MHz,对于X频段约为40 MHz[18]),也可以是测距或遥测谐波信号(带宽介于几百kHz到几MHz之间)。因此,相时延的精度远高于群时延的精度,这说明利用CEI可以获得与VLBI精度相比拟的观测量。
为了获得高精度相时延观测量,需要解决CEI测量中的关键技术——解载波相位整周模糊。如果解模糊失败,则只能得到群时延的精度,在这种情况下,由于CEI基线仅是VLBI基线的1%量级,其技术优势将荡然无存。
1.2 CEI误差分析
CEI测量的是两个天线接收信号的相关相位,信号在由发射至接收的整个传输过程中任何会对电磁波传输产生影响的因素都将在相关相位中引入偏差。该相位可以认为是对干涉时延的测量,单位是观测信号的波长。我们可以把相关相位记作[4]:
(3)
式中:ωRF是射频观测频率,总延迟包括几何延迟、两站之间时钟偏差τclock、对流层和电离层传播介质延迟τtrop和τion、任何未标校的设备延迟τinst和太阳等离子体误差τwind(仅对于深空目标)几部分组成。另外,在每一个测站上均有一个本地振荡器(Local Oscillator,LO),会引入相位偏移ΦLO。2πN代表相位整周模糊度,只有确定了该相位的整周模糊,才能获取高精度的射频信号载波相时延。此外,频率源及时频系统的稳定性还将对相关相位的测量产生影响;信号的信噪比、基线的空间方位不准确性也会影响时间延迟τg的测量精度。
为了校准这些误差因素,通常将一个与待测信号源空间角位置相近的参考源作为基准,将两个信号源的相关相位进行差分,即可消除测站钟差、设备延迟等误差因素,同时可显著降低对流层、电离层、太阳等离子体等误差因素的影响。两个射频信号源(A和B)可观测到的差分相位可以记作:
(4)
由上述分析可知,在进行单差分条件下CEI测量时,要求保证高精度的站间时频信号的同源及同步特性,以减少测量误差;在进行双差分条件下CEI测量时,钟差的因素可以消除,但仍然需要高精度的频率传递技术,确保测站频率的一致性和相干性[19])。
考虑到开展单差分CEI测量时,未标校的设备延迟、站间时间同步的精度、对流层、电离层均会带来较大的测量误差,导致无法解载波相时延(1 ns就会带来0.3 m误差,而S频段波长仅为0.13 m),因此在对精度要求较高的实际应用中一般采用双差分CEI测量或同波束CEI测量。本文下面所描述的便是基于双差分CEI测量的形式。
2 CEI数据处理方法
2.1 高精度CEI信号处理流程
高精度CEI信号处理流程图如图2所示,首先利用两颗卫星的轨道预报得到预报时延,并进行预补偿,然后求解残余相位干涉条纹,并最终逐步求解出精确的干涉时延。
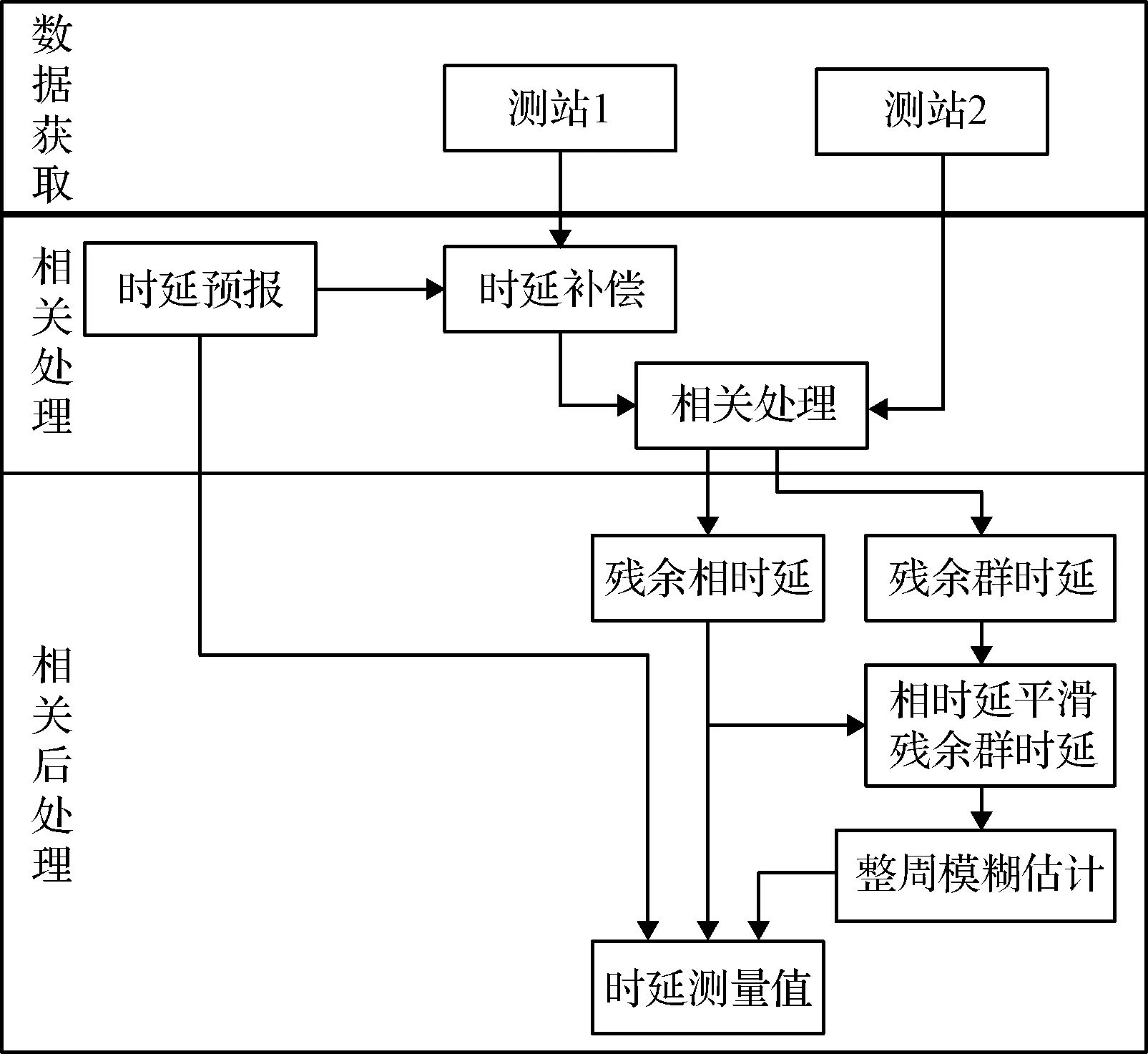
图2 CEI信号处理流程图
具体信号处理流程如下:
1)两个测站分别接收同一个卫星的下行信号,接收信号分别为s1(t)和s2(t),两路信号进行傅里叶变换后为S1(f,t)和S2(f,t);
2)利用已知的卫星到两个测站的时延预报差值对两个频域信号进行时延差预补偿,使补偿后的两路信号残余时延差较小,即:
S′2(f,t)=S2(f,t)·exp(j·2πfRF·τ(t))
(5)
3)时延差预补偿后的两路频域信号做复相关得到残余相关相位:
X(f,t)=S1(f,t)·(S′2*(f,t))=A(f,t)·
exp(jφ(f,t))
(6)
式中:S′2*(f,t)为S′2(f,t)的共轭。
4)利用残余载波相位求解残余相时延,利用残余数据相位求解残余群时延:
(7)
(8)
5)利用残余相时延和载波相位平滑群时延方法平滑残余群时延得到平滑后的残余群时延τgroup_0,sm(t);
6)用平滑后的群时延解算残余相时延的整周模糊度:
N=E[τgroup_0,sm(t)-τphase_0(t)]·fRF
(9)
式(9)中,E为数学期望。
7)整周模糊度乘载波周期再加上残余相时延得到精确的残余时延差值:
τphase_0,real(t)=τphase_0(t)+N/fRF
(10)
8)精确的残余时延差值加上卫星到两个测站的时延预报差值得到精确的相时延观测量:
τphase,real(t)=τphase_0,real(t)+τ(t)
(11)
以上步骤中,第5步“利用残余相时延和载波相位平滑群时延方法平滑残余群时延得到平滑后的残余群时延”是获得高精度CEI观测量的核心,下面将对其方法进行详细介绍。
2.2 相时延解算方法
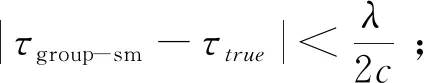
载波相位平滑群时延的基本思路为:将群时延观测量和载波相位观测量相结合,同时利用高精度的载波相位测量值对群时延观测量进行平滑滤波获取平滑群时延,有效降低随机误差,进而提高载波相位整周期的正确解算概率。
由CEI求解得到群时延和相时延分别表示为:
(12)
(13)
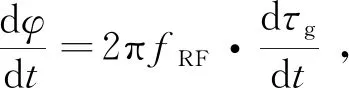
(14)
(15)
理论上,载波相位历元差应该与码群时延历元差相等,即:
τg(tn)-τg(tn-1)≈τp(tn)-τp(tn-1)
(16)
(17)
可由载波相位历元间的差值重建码群时延,即:
τ′g(tn)=τg(tn-1)+τp(tn)-τp(tn-1)
(18)
重建后的群时延误差将被大大压缩。假设从t0历元开始的载波相位观测量持续,并且通常认为群时延测量过程中的随机误差服从高斯分布,则可以通过数学统计的方法将其影响进行削弱。假设已经连续观测了n次,其测量方程可用如下公式表示:
(19)
对以上各式相加求平均,即可得到t0历元的群时延平滑值:
τp(tk)+τp(t0))
(20)
式中:τg,sm(t0)即为t0时刻的平滑群时延平滑值。
下面考虑平滑后的测量误差δ与εg,εp之间的关系。由于载波相位测量的随机误差较群时延测距的随机误差要小得多,即εg≫εp,根据误差传递理论可得:
(21)
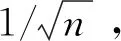
(22)
其中:P(k)表示外推群时延,τphase(k)和τphase(k-1)分别表示k时刻和k-1时刻的相时延,τsm(k-1)和τsm(k)分别表示k时刻和k-1时刻的群时延平滑值,ω(k)表示历元k时刻的群时延权重。

(23)
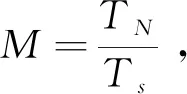
利用S频段下行遥测副载波信号的群延迟差和残留载波信号的相位差进行解模糊算法仿真,其群时延和载波相位平滑群时延估计精度分别为9 ns(信号带宽B=256 kHz,相关信噪比S/N=30 dB)、75 ps,依据公式计算得到平滑因子M的最优取值为120。在M分别取值为60,80,100,120时进行蒙特卡洛仿真统计,仿真次数为1000统计得到载波相位模糊正确解算概率分别为78%,90%,95%,99%,其平滑结果如图3所示。充分说明了平滑因子M取值和解模糊算法的有效性。
3 CEI试验
3.1 试验系统
CEI试验系统利用我国航天测控网喀什地区的两个测控站为基础(以下分别称为测站1和测站2),补充CEI试验所必须的光纤时频传递设备、数据采集与基带转换设备、数据相关处理设备等。两个测站直线距离约20 km,呈东西向排列。
3.2 观测模式设计
试验采用的标校源为BD卫星(目前我国BD GEO卫星的导航电文位置精度优于10 m[20],对应20 km基线时延误差优于20 ps,可作为标校源使
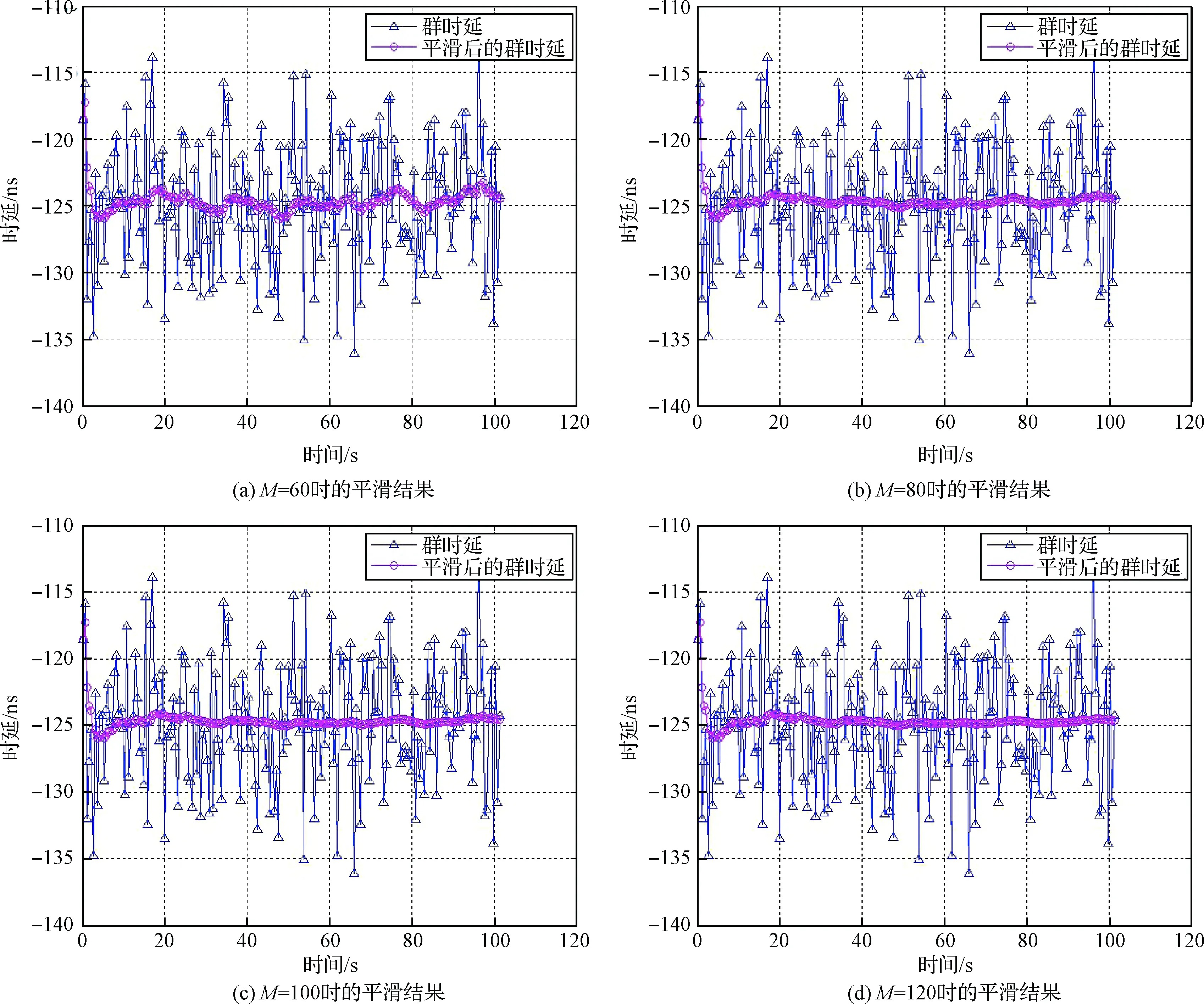
图3 不同M值情况下的平滑结果

图4 基于光纤时频传递的CEI系统构成图
用)。试验目标为TL卫星,两颗卫星角距在10°以内,测控频段为S频段,采用交替观测模式。
其中TL卫星下行信号为标准测控(TT&C)信号,遥测副载波频率65.536 kHz,测距主音100 kHz,实际试验中数据采集带宽为256 kHz;BD卫星下行信号为伪码测距信号,带宽10 MHz,实际试验中数据采集带宽为8 MHz。考虑到TL卫星信号带宽较窄,求取精确相时延整周模糊值的难度较大,因此试验中将TL卫星的观测时间加长,具体实施方式为:先对BD卫星观测7 min,随后停止观测3 min(停止时间内用于测站1和测站2同时切换天线从BD卫星指向TL卫星),再对TL卫星观测17 min,随后停止观测3 min,再切换到BD卫星观测,如此循环,连续观测共计8 h。
3.3 信道标校
由1.2节可知,采用交替观测模式(即双差分模式)可以将站间时差,设备延迟,对流层、电离层等介质误差基本消除干净,但有一点不能忽略,那就是在干涉测量的实际应用中标校源与待测目标源的频率应一致或足够接近,否则会引入下行信道滤波器在不同频点的群时延色散误差。针对此次试验,BD卫星频点约为2218 MHz,TL卫星频点约为2231 MHz,两者相差达到十几MHz,因此必须对CEI下行信道进行标定。利用矢量网络分析仪的实际标定结果如表1所示。

表1 信道群时延色散特性标定Table 1 Calibration of the group delay of the channels
可以看出,在这两个频点上,设备群延时色散约为1.3ns,后续试验数据中应该补偿信道的群时延特性。
3.4 试验实施
试验共进行了4天,每天的观测均从晚上22时开始,开展6~8小时的连续观测。两测站获取到的测量原始数据均先在本地进行磁盘记录,于试验结束后开展事后相关处理分析。
4 试验结果
4天试验的结果相一致,下面给出第1天试验的数据处理结果。先利用卫星的轨道预报值推导出每个SCAN(指一个观测弧段)的时延,利用预报值对测量数据进行预补偿,补偿后的残余相关相位如图5、图6所示。图5为TL卫星的相关处理结果,共15个SCAN,每个SCAN 17 min,间隔10 min;图6为BD卫星的相关处理结果,共15个SCAN,每个SCAN 7 min,间隔20 min。

图5 TL卫星相关处理结果(残余群时延(圆圈)和残余相时延(点))

图6 BD卫星的相关处理结果(残余群时延(圆圈)和残余相时延(点))
由观测量减去理论值能够得到时延残差,这部分残差中包括了各类误差的总和,主要包括设备延迟、站间时间同步误差、对流层误差、电离层误差、热噪声误差,而站间时间同步误差、对流层误差、电离层误差对于两颗星来讲可以认为是一致的,即Δτclock≈0,Δτtrop≈0,Δτion≈0。设备链路的不一致性不能忽略,通过前期标校可知为1.3 ns。
最终获得的相时延观测量与精轨的理论值对比图如图7所示。从图中可以看出,前面几个SCAN的残余相关相位波动较大,后面几个SCAN较为稳定。用BD的残差拟合TL的残差得到TL的测量值,与精轨对比,最大偏差0.16 ns,且随时间变化有变稳定的趋势,稳定在0.1 ns以内。
5 结 论
通过CEI试验系统在20 km基线上开展测量,对BD卫星的伪码测距信号和TL卫星的TT&C信号均成功实现了S频段解载波整周相位模糊。通过BD卫星做标校源,得到TL卫星的精确相时延观测量,该观测量与通过TL卫星精轨反算的相时延理论值相比,精度达到了0.1 ns,对应的GEO轨道精度优于54 m。
此次试验充分验证了文中所提出的相时延解算方法的正确性、可行性,在国内首次实现了在几十km基线量级上利用百kHz窄带测控信号获得无模糊载波相时延。该方法同样适用于对共位GEO卫星的相对定位,具有较好的应用前景,研究成果已经应用于高分专项地面测控系统建设中。

