非线性弹簧形态优化及可调节恒力装置设计

徐 彦，许怡贤，方 琴，从 强，林秋红

(1. 浙江大学航空航天学院，杭州 310027；2. 北京空间飞行器总体设计部，北京 100094)

0 引 言

大型空间薄膜结构具有成本低廉、存储体积小、质量轻、可靠性高等优点，能够实现传统刚性结构很难达到的性能，成为载人航天、深空探测等空间任务的应用热点[1]。在平面薄膜天线和太阳电池阵的工程应用中，为了导入平面薄膜阵面的张拉力，并实现张拉力在热载荷作用下保持恒定，需要设计恒力装置。随着薄膜阵面的尺寸越来越大，需要设计大张力恒力装置，以提高结构基频[2-4]。另外，大型空间薄膜阵面的支撑结构受展开冲击力和各种外部激励作用下容易发生不规则振动，为了防止支撑结构的振动传递到薄膜阵面，也需要在张拉系统中设计恒力装置，以达到减振效果[5]。

恒力弹簧是目前最常见的恒力装置，其随着变形的增大而输出载荷(拉力或扭矩)基本保持恒定，具有载荷恒定、储能密度高、体积小等优点[6]。当单个恒力弹簧的输出力不满足设计要求，可以将多个恒力弹簧组合设计，从而实现输出更大的恒定力。但实际工程应用中，发现恒力弹簧存在以下问题：输出的力不恒定(载荷-位移分析与设计)；薄壁簧片容易失稳；装配固定装置优化设计(减少摩擦力)；收缩过程不按线性方向运动[7]。

近年来国内外学者致力于研究恒力机构，提出了多个设计方案[8]。恒力机构研究主要基于连杆机构准刚体模型(Pseudo-rigid-body model, PRBM)，文献[9-10]首先提出了基于PRBM模型的恒力机构方案，通过优化刚性连杆和弹性元件，实现了恒力输出。基于PRBM模型，更进一步地发展了另一种连杆机构方案[11]。将PRBM模型应用于MEMS系统中的电力接触元件，可实现很小力幅的恒力输出。Pedersen等[12]通过两个层次的优化设计，提出了一种复杂的恒力机构方案，可以实现一定位移范围的恒力输出。这些恒力机构方案输出的力不大，而且恒定力对应的位移行程不长，复杂机构带来的不可靠、重量大和非光滑性，这些缺点限制了其工程应用前景。还有一种恒力装置方案为主辅式恒力弹簧支吊架[13]，采用一对辅助弹簧和摆动刀形凸轮，可以实现在整个过程中机构所提供的力是恒定的。但是该方案的外包络尺寸较大，也比较笨重，而且对凸轮的外轮廓曲线要求很高。

为了实现空间平面薄膜阵面的张拉和减振设计，有必要在包络尺寸和重量的设计空间内实现一种大张力高稳定可调节的恒力装置。本文采用GA算法和非线性有限元法实现非线性弹簧的形态优化设计，并基于组合结构设计张力可调节的恒力装置。

1 恒力装置工作原理

为了设计得到恒力特性(包括输出力大小和补偿位移行程)，恒力装置可以采用组合结构方案，如图1所示，装置中主要功能部件由正刚度的线性弹簧和负刚度的非线性弹簧构成。线性弹簧的载荷-位移曲线如图2(a)所示，具有正的结构刚度k。非线性弹簧的载荷-位移曲线如图2(b)所示，其中ab段为正刚度段，bc段为负刚度段。两者组合后结构的载荷-位移曲线如图2(c)所示，当非线性弹簧的bc段负刚度设计为-k时，组合后结构的载荷-位移曲线具有恒力段de。当预调节力Fa施加于线性弹簧，其载荷-位移曲线发生平移，如图2(d)所示。如果非线性弹簧的设计方案保持不变，则最终组合后结构的载荷-位移曲线如图2(f)所示，从而调节恒力装置的输出恒定力。

图2 工作原理

2 非线性弹簧的形态优化设计

2.1 非线性弹簧设计

负刚度非线性弹簧的设计方案如图3所示，初始的形态曲线可以为任意的B样条曲线，需要通过形态优化设计确定最优的形态曲线。非线性弹簧的力学模型可视为平面曲梁，一端固定，另一端为铰接端，铰接端是非线性弹簧的载荷输出点。平面曲梁为细长构件，几何非线性较强，并且能够提供很长的位移行程。平面曲梁的形态可以用B样条曲线来描述，采用B样条曲线的控制点实现非线性弹簧形态的参数化。对于B样条曲线，随着控制点在设计空间内移动，曲线形状也随之调整。因此控制点的重新定位改变了平面曲梁的几何形态，同时也改变了非线性弹簧的力学特性。

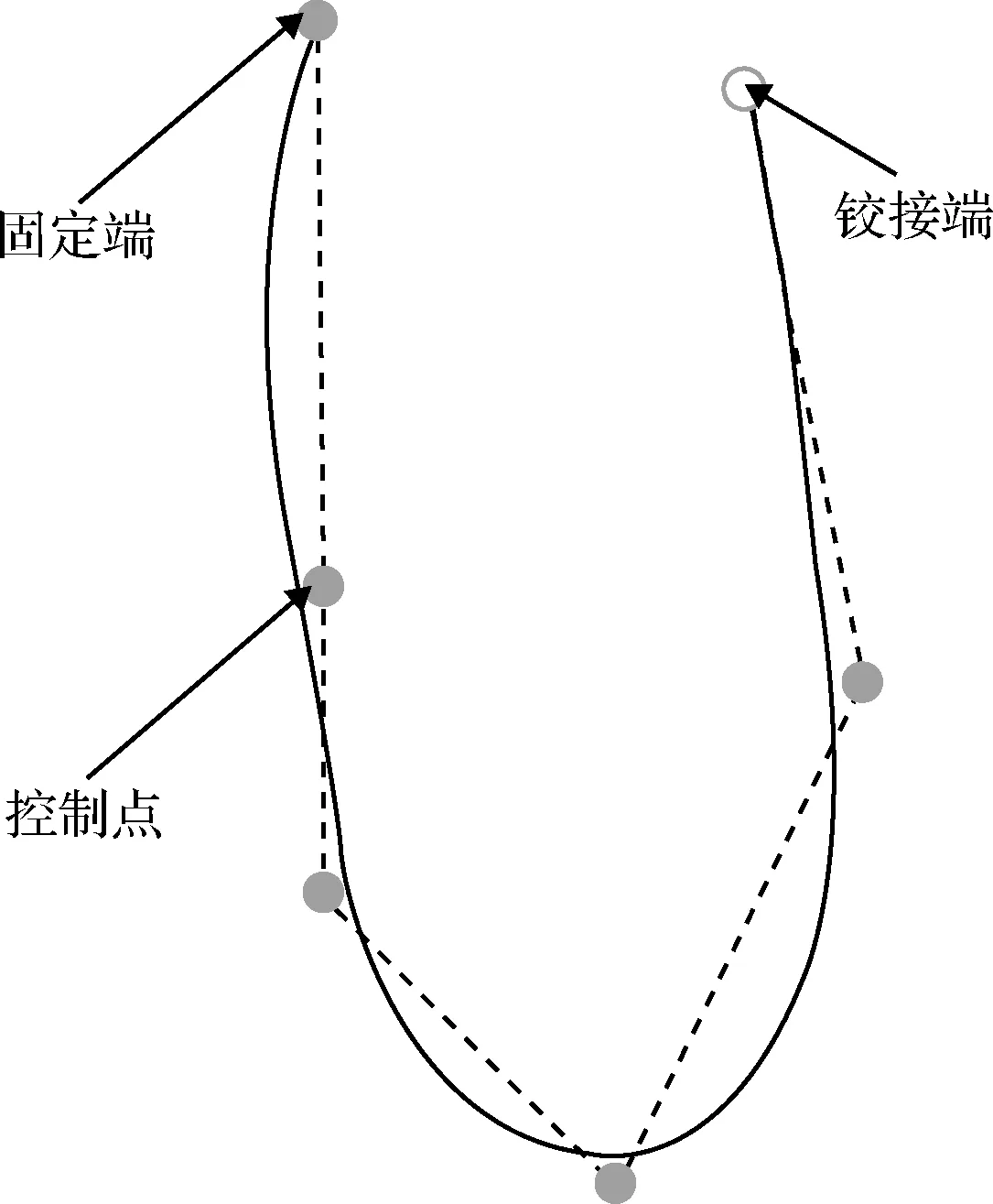
图3 非线性弹簧设计方案

通过建立非线性弹簧的形态优化设计模型，以B样条曲线的控制点坐标及截面尺寸为优化变量，以非线性弹簧的载荷-位移曲线为优化目标，并在一定的约束条件下即可得到非线性弹簧形态的最优结果，从而实现预先设定的载荷-位移曲线。

2.2 形态优化数学模型

形态优化的目标是为了设计非线性弹簧的形态，使其具有如图4中实线的目标载荷-位移曲线，同时满足恒力装置输出恒力大小和位移行程的设计要求。图4中的虚线表示优化过程中一个样本的实际载荷-位移曲线。在优化过程中，每个样本都施加相同类型的载荷。为了设计最优的非线性弹簧形态，需要实际的载荷-位移曲线(虚线)尽可能逼近目标的载荷-位移曲线(实线)。由于无法根据两条载荷-位移曲线的整体偏差建立优化目标，基于曲线上的若干离散点建立优化目标函数(如图中的A～D点)。每个离散点上，两条载荷-位移曲线的相对偏差为Fi。

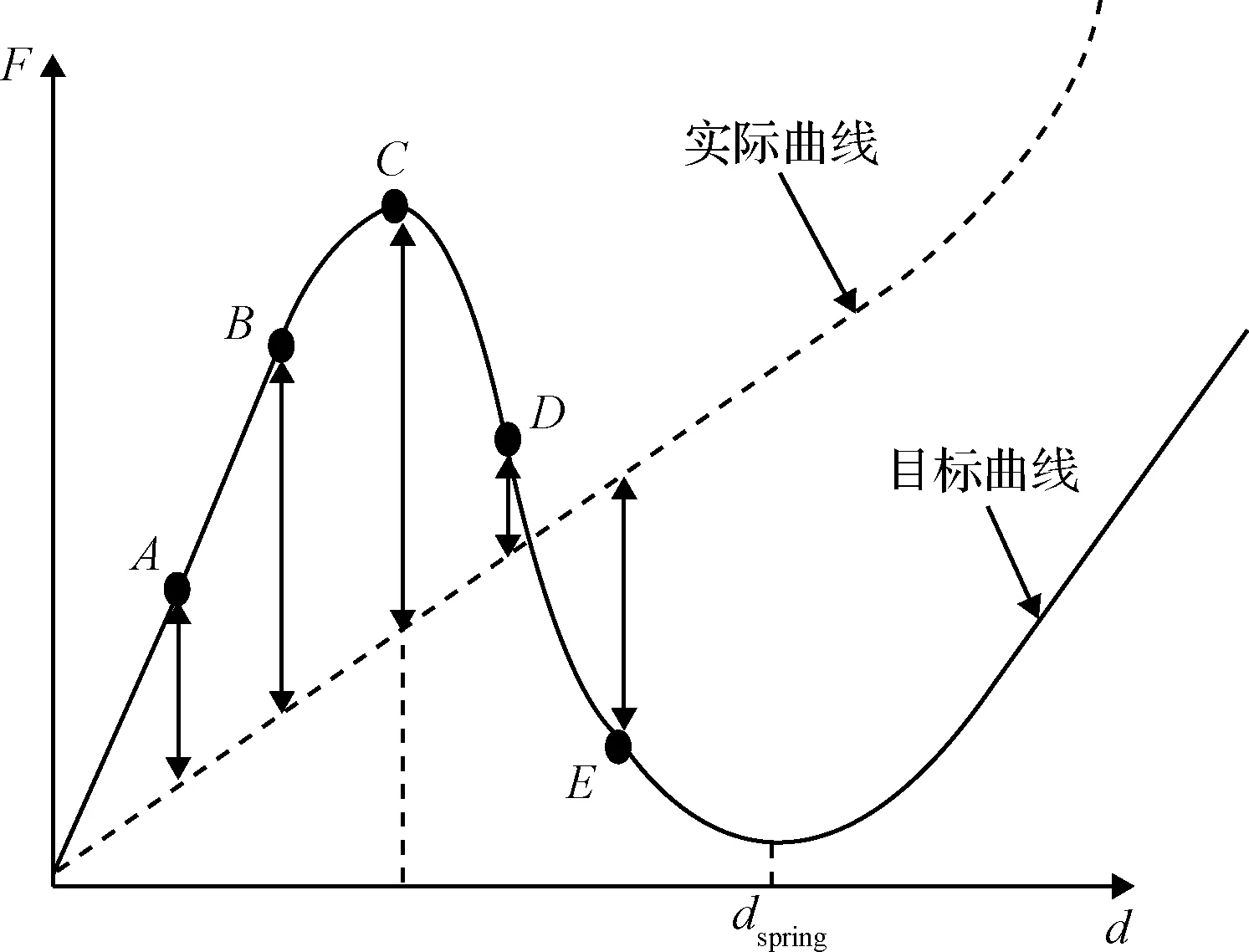
图4 实际和目标载荷-位移曲线

非线性弹簧的载荷-位移曲线偏差可表示为：

(1)

式中：N为载荷-位移曲线上离散点的个数；当弹簧未屈曲时，Fs为实际施加的载荷。

为了实现预定的恒力段位移行程ds，优化目标函数中包含位移惩罚函数f2及其权重系数Wd：

(2)

式中：ds为实际的位移行程，dmin为预定的最小位移行程。

故总的优化目标函数为：

min(f1+f2)

(3)

非线性弹簧形态优化模型中的优化变量包括:B样条曲线控制点的坐标(xi,yi)、约束条件(一端固定，一端铰接)、弹簧面内厚度h1和面外厚度h2等。

约束条件主要包括非线性弹簧的设计空间、弹簧面内厚度和面外厚度的取值范围及最大应力满足强度要求。

(4)

式中：X,Y为优化设计空间，h1max,h2max分别为面内厚度和面外厚度的最大值，[σ]为弹簧材料的屈服应力。

综上所述，非线性弹簧的形态优化数学模型为：

(5)

2.3 形态优化设计流程及实现

非线性弹簧的形态优化设计流程如图5所示。首先建立非线性弹簧的优化设计模型，确定多优化目标如指定的载荷-位移曲线及重量最轻，明确设计变量如工作空间、几何尺寸、材料参数及强度等的上下限范围。然后采用遗传算法(GA算法)结合非线性有限元软件ANSYS完成优化设计，创建若干组随机的设计变量初始值，每组设计变量代表一个设计方案，将设计变量映射到弹簧的有限元模型，对每个设计方案进行非线性有限元分析，进行力学性能评估。如果评估结果符合设计要求，就会检查终止标准。如果不符合设计要求，则生成新的设计变量创建新的弹簧设计方案，并进行新的优化迭代。最终确定非线性弹簧的最优设计方案，可以选择扩展最佳设计方案，以更好地匹配指定的载荷-位移曲线。

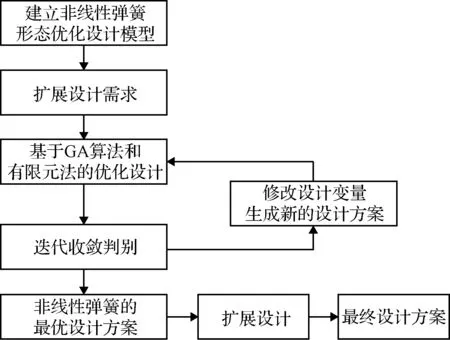
图5 形态优化设计流程

利用MATLAB遗传算法工具箱中GA算法进行非线性弹簧形态优化设计，需要输入适应度函数。对于非线性弹簧的形态优化问题，其目标函数和状态变量需要利用非线性有限元法进行力学仿真才能得到，力学仿真需要借助于成熟的有限元计算程序。而ANSYS软件由于其二次开发APDL语言成为了非线性有限元分析的首选工具。

若要完成MATLAB程序对ANSYS求解器的调用，需要实现MATLAB程序与ANSYS软件之间的数据传递，而二者都有很强的文件操作功能，保证了数据传递的实现可行性。MATLAB在调用ANSYS软件求解器时的数据交互过程如图6所示。

图6 MATLAB和ANSYS的数据交互过程

3 线性弹簧设计

3.1 刚度和强度分析

线性弹簧选用圆柱形螺旋弹簧，其设计参数主要如图7所示。

图7 线性弹簧设计参数

线性弹簧的刚度如下所示：

(6)

式中：G为材料剪切模量，d为弹簧线径，D2为弹簧中径，n为弹簧有效圈数，弹簧总圈数一般为n+(1.5～2.5)。

当弹簧承受轴向载荷F时，钢丝剖面上作用着横向力F和扭矩T，最大应力发生在钢丝内侧，其值为

(7)

式中：C为弹簧直径比C=D2/d，Ks为曲线纠正因数，按经验公式取Ks=1+0.5/C,[τ]为材料的许用应力。

由强度分析可确定弹簧钢丝的直径d为

(8)

为了防止线性弹簧在大幅运动中失稳，在线性弹簧的轴线位置布置非线性弹簧的铰接端导轨，设计弹簧内径D1大于导轨的直径，从而实现线性弹簧的防失稳设计。

3.2 预拉压设计

为了调控恒力装置输出恒力的大小，可以对线性弹簧进行预拉压设计。如图2所示,当线性弹簧预压缩后，输出恒力变小，当线性弹簧预拉伸后，输出恒力变大。为了实现线性弹簧的预拉压，采用如图8所示的设计方案。线性弹簧一端死圈连接在滑块下端面，另一端死圈固定在一个螺母上。螺母拧在导轨上，导轨的外缘加工有螺纹。通过拧动螺母，可实现线性弹簧的预拉压。

图8 线性弹簧预拉压实现装置

4 恒力装置设计及力学分析

4.1 非线性弹簧形态优化设计

根据恒力装置的设计空间，实现非线性弹簧的形态优化设计。非线性弹簧的载荷-位移曲线要求为：力峰值点B对应的力为30 N，位移值为15 mm；力谷点对应的力为10 N，位移值为45 mm。弹簧优化设计空间为：x方向0～30 mm；y方向0～80 mm。弹簧材料采用钛合金，弹性模量为115E3 MPa，泊松比为0.33，密度为4500 kg/m3，屈服强度为800 MPa。非线性弹簧由B样条曲线表征，共有7个控制点，其中第一个控制点固支，另一端约束x向位移，只能沿y向运动。非线性弹簧的面内厚度的约束条件为0.4～2 mm，面外厚度限制为5.0 mm。

根据以上参数建立形态优化模型，形态优化中调用MATLAB遗传算法工具箱实现GA算法，其参数设置为：样本数目为30，优化变量的二进制位数为20，代沟为0.09，变异概率为0.01，终止进化代数为100。经过形态优化设计，得到了最优的载荷-位移曲线如图9所示，由分析结果可见实际的载荷-位移曲线逼近优化目标曲线，非线性弹簧最优形态曲线能够满足设计要求。

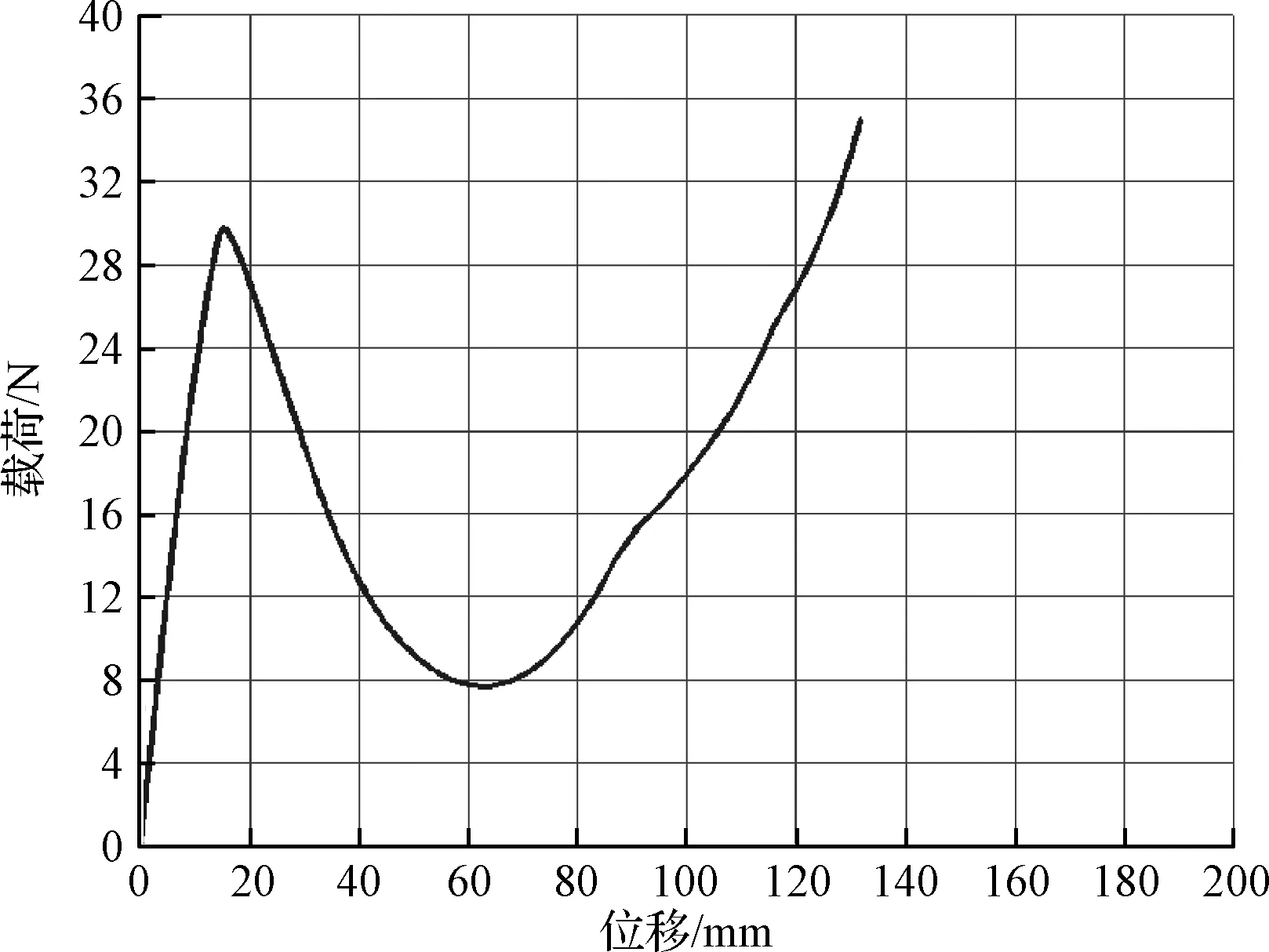
图9 优化后的载荷-位移曲线

优化得到的非线性弹簧形态曲线如图10所示，B样条曲线控制点的坐标如表1所示。建立非线性弹簧的有限元模型，在ANSYS软件中采用BEAM188单元模拟非线性弹簧，一根非线性弹簧共划分163个单元，非线性弹簧的面内厚度为1.189 mm。非线性弹簧发生最大位移时的构型如图11所示。

图10 优化得到的B样条曲线

表1 B样条曲线控制点的坐标Table 1 Coordinates of control points of B-spline curve

图11 最大位移时的构型和应力分布

4.2 线性弹簧性能分析

根据恒力装置的工作原理，线性弹簧的拉压刚度需要和非线性弹簧的负刚度相匹配，通过拟合如图11所示的非线性弹簧的载荷-位移曲线，得到了其负刚度为0.686 N/mm。线性弹簧的材料选用SUS304，剪切模量为70 GPa。弹簧线径为d=0.895 mm，弹簧中径为D2=8 mm，弹簧有效圈数为n=18，原始长度为75 mm。根据式(7)可计算得到线性弹簧的刚度为0.685 N/mm。在恒力装置工作过程中，线性弹簧的最大压缩长度为45 mm，根据式(9)可计算得到线性弹簧的最大应力为585 MPa。

由于恒力装置的外包络尺寸限制，线性弹簧可以实现预拉压的行程约为20 mm，则恒力装置的输出恒力可以调节的量为20×0.686=13.7 N。故可以通过预拉压线性弹簧，可以实现恒力装置输出恒力的调节，恒力范围约为[26, 54]N。

4.3 组合结构的性能分析

基于前述的非线性弹簧和线性弹簧方案，进行组合结构的性能分析和评估。在非线性弹簧有限元模型的右侧铰接端增加正刚度的Y向线性弹簧。在ANSYS软件中采用COMBIN39单元模拟线性弹簧，其载荷-位移曲线定义见表2。线性弹簧上端固定，下端和非线性弹簧连接，非线性弹簧的约束条件同前。

表2 线性弹簧的载荷-位移曲线Table 2 Load displacement curve of linear spring

对组合结构进行静力分析，得到了载荷-位移曲线如图12所示，即为组合结构的最终载荷-位移曲线。由分析结果可知，当位移增加到13.7 mm时，载荷为40 N；当位移继续增加时，即进入恒力段；当位移增加到34 mm时，载荷达到恒力段最低值40.4 N；当位移增加到45 mm时，载荷为42.2 N。恒力输出值为40 N，恒力段的变化幅值为4.5%，位移行程满足15～45 mm的设计要求。

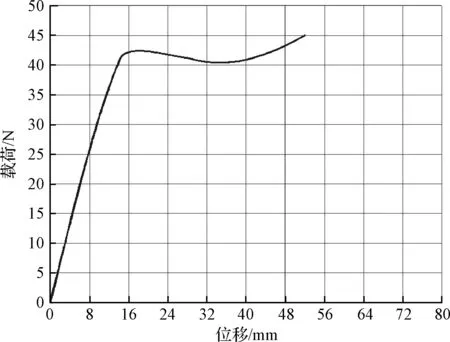
图12 载荷-位移曲线

组合结构变形过程中，右端铰接节点的x向支座反力在18～25 N之间变化。为了校核装置中导轨的变形情况，将导轨按两端固支梁建模，不锈钢导轨的长度为100 mm，截面直径为3 mm。进行多个典型状态的静力学分析，得到导轨的最大侧向变形为0.16 mm，可以看出导轨的变形量不大，不会引起右端铰接节点运动过程的卡轨现象。

4.4 部组件功能设计

基于前述的组合结构设计方案和力学特性，进行恒力装置设计。恒力装置由外包装盒、非线性弹簧、线性弹簧、导轨、滑块及张拉索等组成，如图13所示。

每个恒力装置包含四组组合结构，每组组合结构中的滑块上设计有2个耳板，两根张拉索分别一端固定在滑块的耳板上，另一端穿过装置顶板上的孔，如图14所示。然后绕过外包装盒顶板上的滑轮，最后合并成一根输出的张拉索。张拉索通过滑轮，可以改变力的方向和保持力的大小，从而实现恒力装置输出恒力能在±45°范围内调节方向。

图14 张拉索绕过滑轮组

每根非线性弹簧一端固定，另一端铰接。固定端采用3×M3螺栓连接于恒力装置的底板。为了保证非线性弹簧铰接端沿着垂直于恒力装置底板的方向运动，需要设计铰接端的导向装置，采用滑块/导轨设计，如图15所示。为了减少滑块运动过程中的摩擦力，滑块和导轨之间可以设计直线轴承。

图15 基于滑块/导轨的导向装置

为了保护恒力装置，防止非线性弹簧铰接端位移过大，需要在导轨上合适的位置设计滑块的限位装置。在导轨相应的位置加工一个凸台，当滑块运动到此时被限位，从而当位移变化超出恒力段范围时，恒力装置有大的输出力以进行自我保护。

恒力装置的装配次序如下：先将非线性弹簧铰接端和滑块连好，然后将滑块和线性弹簧套在导轨上，接下来将导轨一端和非线性弹簧固定端固定在包围盒底板，从滑块的耳板上引出张拉索，最后将包围盒顶板盖上并固定导轨的另一端，将张拉索穿过顶板上的孔，最终绕过滑轮组并张拉薄膜面阵。

恒力装置在轨服役期间要经受真空、热循环、辐照、原子氧及碎片等空间环境的作用，需要进行环境适应性设计。恒力装置外包围盒采用铝合金材料，尽可能实现密闭设计和轻量化设计，并在外侧包裹柔性热防护材料。非线性弹簧采用钛合金，而导轨和滑块采用和钛合金膨胀系数较接近的不锈钢。外包围盒顶板上的滑轮、轮轴及支架都采用钛合金，减少滑轮侧隙在热环境下的变化。

5 结 论

面向平面薄膜天线和太阳电池阵中薄膜阵面张拉系统的工程应用，本文研究了一种基于非线性弹簧的形态优化设计方法，并应用于可调节恒力装置，得到了以下结论：

1)建立了非线性弹簧的形态优化数学模型，基于GA算法和非线性有限元法实现了形态优化设计，得到了非线性弹簧最优的形态曲线，力学分析结果表明非线性弹簧的载荷-位移曲线能够逼近设计曲线。

2)提出了可调节恒力装置的组合结构工作原理和设计方案，完成组合结构的力学特性分析，结果表明该方案能够在较大的位移行程内输出大张力高精度恒力。

3)通过部组件功能设计，表明恒力装置可以实现自我保护、恒力大小/方向可调等功能。

后续将着重开展恒力装置的疲劳性能分析，并进一步细化方案设计和环境适应性设计，最终研制样机并开展地面试验验证研究。