空间目标碰撞概率的等效矩形域快速算法
董文朴,任磊生,周 浩,陈 鸿,兰胜威,李 毅
(中国空气动力研究与发展中心,绵阳 621000)
0 引 言
近年来空间碎片问题日益严峻,给空间资源利用的可持续发展带来了极大的阻碍。截止到2018年4月,地球外层空间编目的10 cm以上空间物体多达18900,其中空间碎片占到60%以上[1]。空间碎片不断增加的主要因素有航天器碰撞或爆炸解体过程和空间碎片相互碰撞解体的反馈连锁效应等[2-3]。为了使空间碎片切实可控,已经开展大量空间目标的碰撞解体和碰撞预警研究,用于碎片减缓、防护设计、监测预警等目的[4-6]。
依照解体模型[7],空间目标解体过程产生的碎片轨迹可以进行预报分析。如果能够将碎片轨迹精确预测,则航天器可以提前采取规避措施,避免碰撞风险。但是解体模型和轨迹预报会引入一定误差,这使得碰撞变成概率事件。计算空间目标碰撞概率成为风险评估的一个基础问题。在空间两目标相互靠近的过程中,根据轨道预报模型可以对交会时刻状态进行预报,预报的精确度和初始误差的传播决定了交会时刻的误差分布[8-9]。一般情况下空间目标相交会的速度较大,交会瞬间可以近似为瞬时过程。在这种情况下,假设目标在相遇期间速度保持不变,位置误差保持不变,交会目标的运动近似为线性相对运动。在线性相对运动假设下,交会目标的碰撞概率计算可以转换到交会平面上去求解,则把三维问题转换成二维平面问题进行计算,使得计算问题得到简化,提高了碰撞概率计算速度[10]。
在空间目标碰撞概率预警工程中,要面对大量的碎片碰撞概率计算和预测,所以交会平面二维积分的计算速度直接影响了预警速率。针对空间目标交会平面的碰撞概率计算问题,王华等[11]研究了三种简化方法,一是将概率密度函数等效成均匀密度分布进行简化计算;二是将二维积分问题转化为一维曲线积分[12];三是数值求解。这三种方法各有优缺点,但是在精度和计算速度上不能同时满足要求。安喜彬等[13]提出梯度数值积分方法,将椭圆区域积分转化为适量的微元进行求和计算,减少了数值积分计算密度,但不利于解析分析问题。白显宗等[15-16]在Chan[14]提出的等效圆域法基础上,提出空间压缩无穷级数方法,该方法将概率积分转化为级数解,通常选取级数首项在保证计算精度的同时,提高了计算速度,同时该算法可以对交会目标最大碰撞概率进行评估[17]。本文基于等效圆域法的思想,提出等效矩形域法对概率积分进行近似求解。在空间目标交会算例中显示,等效矩形域法比空间压缩无穷级数法有更好的稳定性,适用于碰撞概率预警评估。
1 空间目标碰撞概率的计算
1.1 碰撞概率计算的提出
对于相互靠近的两个空间目标,可以通过轨道模型预测两目标交会时刻,给出最接近时刻和最接近距离。具体计算中将两目标状态分布合并考虑,给出在交会时刻相对位置状态概率分布,也就是联合概率分布[10]。对于状态误差为正态分布的空间目标,两目标的联合概率分布仍然为正态分布,使得联合误差协方差矩阵等于两目标协方差矩阵之和。联合误差分布在坐标空间中的等概率面为椭球形,对协方差矩阵进行对角化,可以得到误差椭球的三个半轴σ1,σ2和σ3:
(1)
联合分布给出了两个空间目标在交会时刻的相对位置误差分布。如图1所示,在线性相对运动假设下建立交会坐标系,其中平面xy为目标交会平面,z轴指向相对速度方向,最接近距离为ρh。误差椭球在交会平面xy的投影半径为σx和σy,其中x轴为半长轴方向。由于在轨空间目标尺寸形状不一,为了方便处理分析,将目标等效成相应尺寸的球形目标。在交会时刻,如果两目标质心相对距离小于两目标的等效半径之和,则认为碰撞发生。在交会坐标系中,利用投影将两目标的碰撞概率,转化为半径为R的圆域内的联合误差积分:
(2)
式中:积分区域S为x2+y2≤R2,μx和μy分别为ρh在坐标轴上的分量。
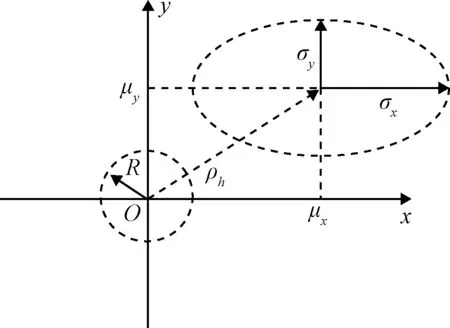
图1 联合误差椭球在交会平面的投影示意图
1.2 等效矩形域法计算碰撞概率

图2 等效矩形区域

(3)
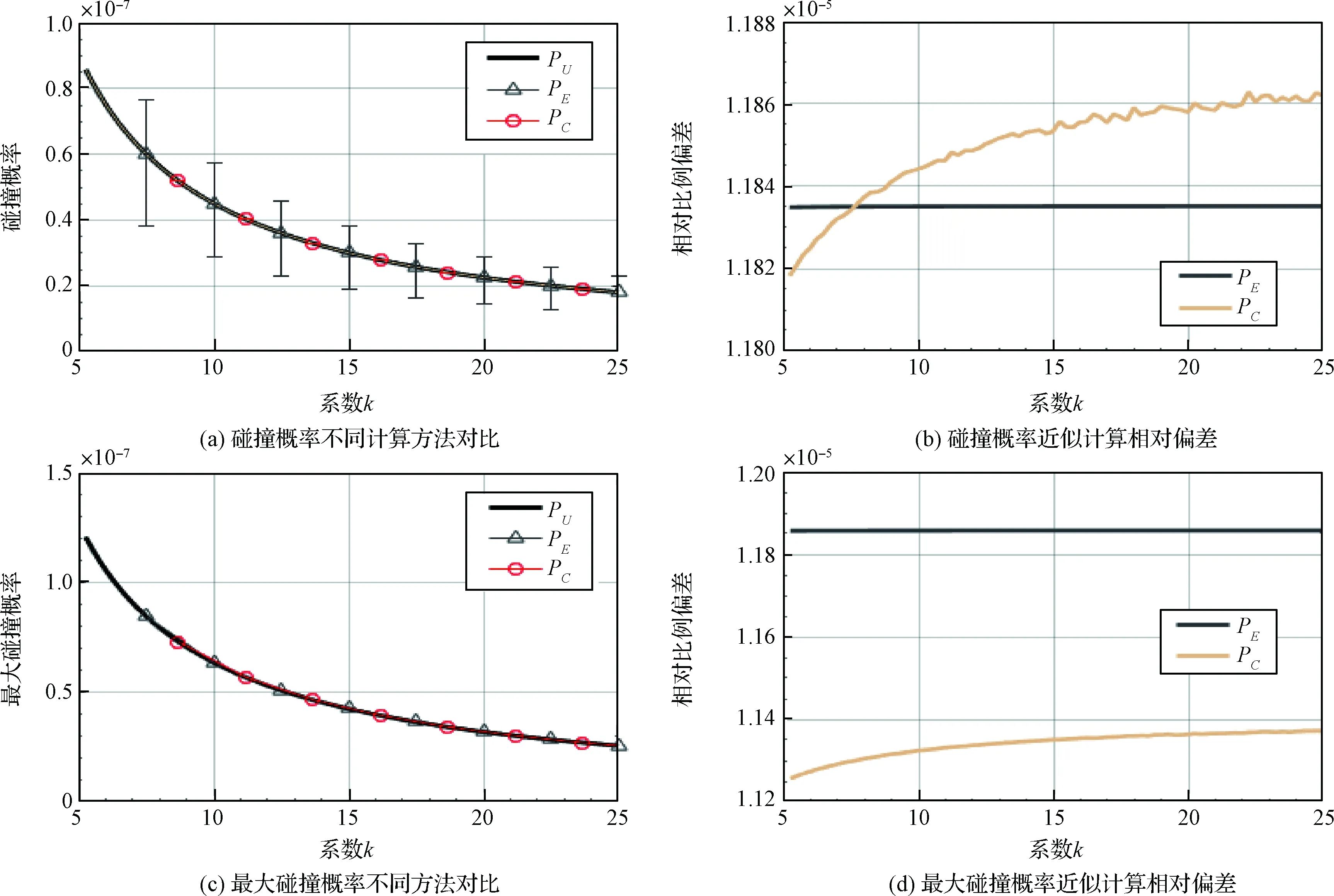
其中,Φ(x)为标准正态分布函数。在等效矩形域下,二重积分公式近似成解析形式,使得二维积分计算得到简化。同时根据积分域范围给出等效矩形域法的误差范围,从图2可以看出,当矩形域外接积分圆时,可以得到积分PU的近似最大值Pmax,内接时得到最小值Pmin,则有Pmin 随着空间目标的误差椭球形状和大小的变化,碰撞概率存在最大值。当目标误差不确定时或者被冲淡时[18],最大碰撞概率可以为空间目标接近状态评估提供参考。利用等效矩形域法来近似求解误差椭球形状比例已知的碰撞概率最大值。对碰撞概率计算式(2)可将误差椭圆半轴作等比例变换: (4) 图3 积分区域S′示意图 在二维积分PU作等比例变换后,将其转变到极坐标系进行求解,令: (5) 在坐标变换下,式(4)可改写为: (6) (7) 根据式(7)对σy求导,可以得到: (8) 在椭圆长短轴比例为k的情况下,当σy=σM时,根据式(3)得到最大碰撞概率PM。 选取两个算例进行验证:算例1来自于空间目标编号为27430和28064在交会时刻2005年3月8日10:11:56.599LT的交会状态参数[19-20];算例2为假设空间两目标接近相撞时的交会状态参数。算 例1和算例2的交会状态参数在表1中给出。 表1 交会时刻状态参数Table 1 The position parameters at the encounter time m 图4 算例1碰撞概率随系数k的变化 对于算例1,假设联合误差椭球在交会平面的投影均方差为σy=20000 m,σx由第1.3节中的比例系数k给出。在给定状态下,空间目标碰撞概率随系数k的变化结果如图4所示。其中,碰撞概率积分式(2)的数值积分结果如PU所示,PE为利用等效矩形域方法近似求解结果。为了对比等效矩形域方法,利用基于空间压缩无穷级数快速方法计算碰撞概率积分[15-16],在该方法下,考虑计算效率以及收敛性,通常选取首项进行近似分析,根据首项得到的概率积分式(2)近似为: (9) 利用式(9)计算得到的结果用PC表示。 图4(a)中显示,对于算例1中的目标交会情况,空间目标在交会时刻的相对距离较远,碰撞概率整体处在10-7量级,同时给出不同方法的估计范围。随着k的增加,碰撞概率继续下降。两种近似方法与数值积分法得到的曲线相一致,计算结果基本重合。为了进一步对比不同方法的近似程度,取近似值与数值积分值的相对偏差,将相对偏差与数值积分值作比,得到相对比例偏差曲线,如图4(b)所示。PE和PC的近似结果与数值积分结果的相对偏差在同一个数量级。但是,当系数k增大时,也就是误差椭球被拉长时,PC的近似值偏差增大,而PE近似偏差相对较为平稳。 在图4(c)中,给出了最大碰撞概率随均方差比例k的变化。在算例1交会情况下,两种近似方法估计的最大碰撞概率结果都与数值方法相吻合。在图4(d)中给出对应的相对比例偏差结果,显示出与碰撞概率相对比例偏差相类似的趋势,估计偏差都在10-5量级,曲线PC的最大碰撞概率估计值随k的增长偏差增大,而等效矩形域法给出的结果PE相对稳定不变。 对于算例2,两个空间目标相互靠近,在交会时刻接近距离为100 m,目标的联合半径为10 m,两目标接近碰撞,此时假设σy=10 m,碰撞概率随系数k的变化情况如图5(a)所示。对于算例2,可以看到空间压缩无穷级数法PC给出的近似结果与数值方法PU偏差较大。在图4(b)中给出了PC与PU对应的相对比例偏差结果,可以看到在系数k接近30时,相对偏差达到9%。对于等效矩形域法,估计结果PE随k的变化仍然与数值结果PU保持较小的偏差,并且能够随k的增长保持稳定。 在图5(c)和图5(d)中给出了两种方法对算例2的最大碰撞概率估计。在算例2情况下,最大碰撞概率PU随k的增长持续增加。等效矩形域法和空间压缩无穷级数法给出的最大碰撞概率估计结果PE和PC,显示出相同的趋势。系数k在5~25范围内时,PE与PC作对比分析,等效矩形域法PE与数值计算结果PU更为接近,等效矩形域法的估算基本在1%以内。 图5 算例2碰撞概率随系数k的变化 结合算例1和算例2对不同碰撞概率近似方法进行计算效率分析。在计算碰撞概率过程中,等效矩形域法(式(3))中包含正态分布函数的积分运算。正态分布函数被广泛应用于工程计算中,在算法和应用上较为成熟,其函数在Cmath库和GSL等科学计算库中都有调用。为了分析碰撞概率计算效率,在具体采用了误差函数展开法[21]和调用GSL库函数[22]两种方法进行等效矩形域法算法实现,并与空间压缩无穷级数法和数值积分法进行对比,其中算法实现语言为C++。表格2给出了算例1和算例2在比例系数k为5时不同方法的计算时长,其中计算结果保证4位有效数字的精度。 表2 计算时长Table 2 The calculation time s 表2给出了不同方法计算碰撞概率的时长,其中,PU为数值积分方法,PE-GSL和PE-erf分别为采用GSL库函数和误差函数展开方法求解的等效矩形域方法,PC为空间压缩无穷级数法,计算时长为重复计算107次的平均CPU耗时,不同计算平台和编译环境的绝对时长可能会有差异,所以这里只作相对分析。计算结果显示,PE和PC比PU有两个数量级以上的优势。PC用时最短,PE-GSL和PE-erf时长为PC的1~4倍左右。计算结果表明,等效矩形域方法可以达到与空间压缩无穷级数快速算法相同量级的计算速度,可以利用其实现对碰撞概率的快速预测。 本文基于误差椭球交会平面投影算法,对接近空间目标碰撞概率的计算方法进行探讨,提出了等效矩形域快速计算方法。等效矩形域方法是将交会平面内的碰撞概率积分域用等效矩形域代替,简化了二维积分,得到了形式更简单的碰撞概率解析近似式。在空间目标误差椭球形状比例已知的情况下,利用等效矩形域方法推导了空间目标的最大碰撞概率计算方法,可用于快速评估相互接近的空间目标危险程度。 本文选取两个算例进行计算分析,并与空间压缩无穷级数近似法相对比,计算结果显示了等效矩形域方法快速估计概率积分的可靠性。同时,等效矩形域方法可以适应不同的联合误差椭球半轴比例情况,并且与数值结果的偏差随半轴比例增长变化缓慢。特别在空间目标相互靠近的情况下,本方法的估计精度要优于空间压缩无穷级数方法,在碰撞预警评估中,有助于对大量靠近的相遇实例进行碰撞概率快速对比评估。1.3 基于等效矩形域法的最大碰撞概率计算
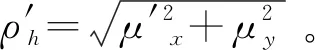


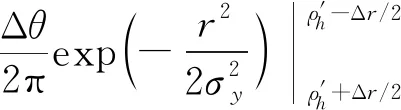
2 算例分析



3 结 论

