动静结合建构数学模型
刘红霞
[摘 要]平移和旋转这部分知识,旨在通过生活情境来指导学生理解平移和旋转的概念。将“动”与“静”的特点融入教学中,借助“淘气的圆片”设计生活化数学情境,指导学生运用数学符号、肢体动作、思维想象、逻辑语言等形式来建构具有动静结合特点的数学模型,对学生的数学知识与综合能力的培养,以及兴趣的激发有重大帮助。
[关键词]平移和旋转;动静结合;数学模型
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)02-0068-02
数学模型是利用数学语言、符号或者其他形式,将书本知识转化为直观的数学结构,该结构能够反映知识内部各要素之间的联系。小学数学教学力求在建构数学模型的过程中尽可能让模型动起来,以动静结合的形式来反映知识的本质,从而激发学生的学习兴趣和积极性,让学生体验到数学好玩、数学有趣。
一、动静结合构建数学模型理论基础
动静结合构建数学模型的过程中,无论是模型处在静态,还是动态,都离不开学生的参与,静态过程中重点在学生思维参与,动态过程中重点在学生实践操作参与,都是培养学生多项智能的过程,所以研究的第一个理论基础就是加德纳多元智能理论。当模型展现在学生面前,对学生来说是一个刺激,特别是动态化模型更能够吸引学生的注意力,激发学生的学习兴趣,所以研究的第二个理论基础是布鲁纳的学习动机理论,即学习最好的动机是对学习材料的兴趣,这里激发学习动机的是数学模型。
二、在“平移和旋转”中构建动静结合模型
在“平移和旋转”教学中,以“淘气的圆片”为起点,展示圆片运动和静止的过程,引导学生联系实际思考和探究,应用数学符号、工具、方法,以及肢体的动作来构建数学模型。
1.情境导入中探索模型
教师通过交互式电子白板展示一个在屏幕上一直跳动的圆片,教师通过鼠标将其固定:“如果再次点击鼠标,这个圆片会怎样运动呢?”点击鼠标,让学生观察圆片运动的情况。学生将圆片运动的特点分为淘气时没有规则的运动,以及听话时有规则的运动。教师继续提问:“圆片有规则运动时,出现了几种运动方式呢?”学生回答:“有两种。一种是向前冲,一种是绕圈圈。”为了让结果现实化,教师指导学生用手掌来模拟向前冲和绕圈圈的过程。
设计意图:课堂上如果直接让学生说出平移和旋转的事例和特点,学生可能会很难说出。教师以逆向的方式直接展示平移和旋转的情境,让学生在分析圆片运动的特点后,利用生活化语言“向前冲”“绕圈圈”来概括运动特征,奠定了后续建模的基础。
2.多样化模型建构过程
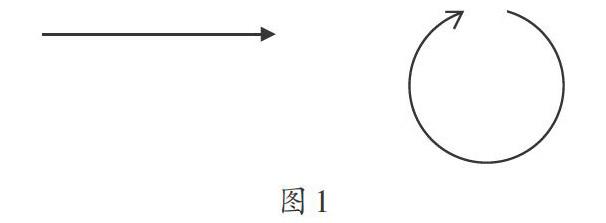
结合加德纳多元智能理论,以发展学生的各方面智能为目标,展开不同形式的模型建构。第一阶段,教师鼓励学生建构模型:“哪位同学可以将刚才小圆片‘向前冲和‘绕圈圈的过程,通过不同形式表达出来?”大部分学生是用手指头来表示两种运动的过程,少部分学生画出一条细线和一个没有闭合的圆表征运动的过程。教师肯定了学生积极思考的态度后,启发学生:“两条以上的直线相交后,至少会形成一个平面图形;箭头可以代表方向,像直线和箭头都属于基本的数学符号。可否结合数学符号对所画的细线和没有闭合的圆进行改进呢?”学生认真思考后,画出了一条标有箭头的线(如图1),笔直的直线代表圆片“向前冲”的运动状态,在没有闭合的圆上画一个箭头,代表转圈圈的方向。这是第二阶段结合数学符号来建模。第三阶段,教师要求学生利用生活中常出现的模型作为本节课模型建构的工具,也就是对模型再建构。首先建构圆片“转圈圈”的模型,一位学生发现风扇的转动类似圆片“转圈圈”的过程,但是还需要教师以风扇为例再建构模型,从而得出真实的数学模型。教师可指导学生通过自身的行为来展现风扇转动的特点,比如,教师下指令“风扇低速旋转”,该学生用很慢的速度转动自己的身体;教师下指令“风扇快速旋转”,学生即刻将身体转动的速度调快。类似于该种方法,学生通过低速步行和高速步行的形式来表示自行车向前行驶的快慢。
设计意图:本阶段教学是引导学生通过实际参与的方式,建构导入情境中所展示的圆片运动的模型。建构的形式逐层递进,第一次建构是让学生自由发挥,由于小学生的思维能力比较弱,因此第一阶段建构的模型过于简单。第二阶段开始引导学生调动已有的知识建构模型,让学生思考如何运用数学符号优化模型,属于静态模型,培养了学生的数理逻辑智能。第三阶段教师再次深化,不仅仅引导学生将现实生活中存在的模型展示于课堂,还要求学生对模型进行再建构,主要是通过肢体运用来还原动态化的模型,初步地将动、静两种模型展示于课堂,培养学生的身体运动智能。
3.分析模型,讲解新知识
教师分析学生建构的模型后,引出本节课的新知识“生活中类似风扇转动、车轮转动等现象称为旋转;类似运动员跑步、电梯升降等现象称为平移”。学生对新知识有所了解后,教师要求学生通过演示模型表征平移和旋转的特征。其中一位学生以铅笔作为模型建构的工具,展示用手向前推动铅笔即为平移的过程,两个手指头握住铅笔的中间或者顶端使其转动即为旋转的过程。随后该学生归纳平移的特点为“物体都是直直地向前移动”,旋转的特点为“物体要么以自己的中点为中心转动,要么以顶点为中心转动”,在教师指导下,该学生知道物体的中点和顶点属于旋转中心,按照这位学生的思路,也就是旋转的中心始终是在物体上。该学生归纳的是否全面呢?教师将教室的前门作为模型建构的工具,轻轻关上门,然后再打开,要求学生思考:“在这个过程中,门最外侧的塑胶条是在做平移运动还是旋转运动呢?”有學生认为塑胶条并不是直直地向前运动,它是做旋转运动,绕着门框轴旋转。随即教师在白板中画出两条平行的细线,A线代表塑胶条,B线代表门框轴,A线绕着B线转动。教师归纳:“对塑胶条而言,旋转的中心并不是在物体上,而是在物体的外侧,所以判断该物体是否作旋转运动时,关键是要找到旋转的中心。旋转中心并不一定在物体上,有可能在物体外部。”
设计意图:通过分析已建构的模型讲解新知识,能使知识更加直观生动。为了找出学生在知识理解上的缺陷,再次要求学生展示生活中的动态化模型,说出平移和旋转的特点,列举能够反映概念全部特征的模型,让学生思考分析,最终自主地完善概念,有效培养学生的内省智能。该阶段也是以动态化模型为例,讲解新知识及完善新知识的过程。
4.拓展迁移设计模型
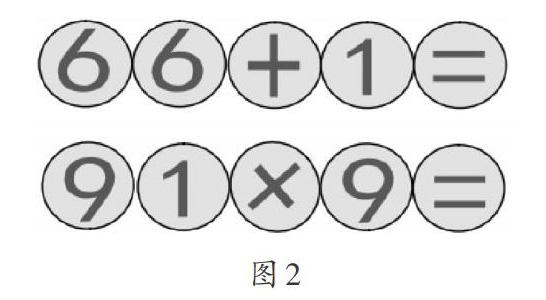
学生掌握了新知识后,教师以模型设计为主题来引导学生巩固新知识。教师利用信息技术将小圆片浓缩为一个点,随后这个点在白板上经过平移和旋转运动,得到not(没有)这个英文单词,随后通过动画形式展示字母“t”和字母“n”平移后得到ton(很多),可见只要一次平移就能够组合成一个新的单词。 动画的刺激以及变魔术搬的单词转化过程,瞬间激发了学生的学习兴趣。教师要求学生以小组为单位,发挥聪明才智设计一个模型,将该模型中的部分要素进行平移或者旋转,就能够改变该模型的内涵。其中一组的学生将数学算式中的数字和符号进行平移与旋转,进而将算式的数值调整为最大。为了让教学更加直观,如图2所示,教师通过信息技术展示最初的算式和最终的算式:上方是最初算式,可以看出,将1进行平移,将6进行平移和旋转,并将“+”进行旋转,就可以得出最终的计算结果最大的算式。最初算式是第一个构建的模型,属于静态模型,教师通过动画展示数字和符号平移与旋转的过程,就使模型变为动态,这种动静结合的形式,让学生感受到平移和旋转在学习和生活中的应用。
设计意图:结合布鲁纳学习动机理论,在学生对英文单词学习材料感兴趣后,趁热打铁要求学生自主构建模型,培养了学生的自然探索智能,同时动静结合下的模型更生动地展现了知识的应用价值。
建构模型是去除知识非主干成分,保留精华,并将知识形象化的过程,结合小学数学教学内容,将动、静两种形态的模型展现在课堂上,并引导学生自主建构模型,对培养学生的学习积极性和各方面智能有积极作用。
[ 参 考 文 献 ]
陈鸿.借助“三慢”策略 引导学生建立数学模型[J].小学教学参考,2017(20).
(责编 金 铃)

