小学数学深度学习路径探索

陈文龙

[摘 要]以培养学生核心素养为目标，对小学数学深度学习路径进行积极探索，指出深度设计是深度学习的前提，自主思考是深度学习的根本，拓展延伸是深度学习的深入。

[关键词]深度学习;路径;小学数学

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）02-0049-02

深度学习相较于浅层学习而言，它更加注重学生学习的情境性和主动性，更加强调知识之间的关联性，更加看重反思性思维的构建，是一种指向更高阶思维的学习模式，也是学生数学核心素养真正落地的重要途径。

一、深度设计是深度学习的前提

教学设计是整个课堂的理论框架，也是教学实践活动的基本蓝图。优秀的教学设计应该具有情境性、渐进性、整体性等特点。情境性指的是要顺其自然地把学生带入问题情境当中，把数学学习与现实生活紧密联系起来;渐进性指的是教师在课堂设计过程中要树立阶梯式的问题设计理念，要不失时机地引发学生的思考，使学生经历由未知到已知、由浅显到深入的学习过程，不断提高学生对问题的认识水平;整体性指的是教学设计要兼顾教学活动的各个环节，使学生能够体验到解决数学问题的整个过程，从而有利于学生从整体上把握知识点的来龙去脉，实现“学会知识”和“运用知识”的无缝对接，最终提高学生解决数学问题的能力。

如，“近似数”中“进一法”教学片段：

师：上节课我们学习了“四舍五入”，这节课我们学习“进一法”。

师：学校组织春游，需要乘坐观光车。李老师一共带了19个学生，而每辆观光车只能乘坐5个人。请大家帮李老师算一算一共需要几辆观光车。

生1：19÷5=3.8，按照“四舍五入”可得需要4辆观光车。

生2：这个算法不对。李老师也需要乘坐观光车，所以应该是（19+1）÷5=4（辆）。

师：生1和生2的计算结果一样，但是思路不同，他们谁的正确呢？

生（异口同声）：生2对。

师：是的，因为生2考虑到了李老师也要乘坐观光车的现实问题。现在把这道题变一下：如果李老师带了20个学生，那么需要几辆观光车呢？

生1：这次我记住了，应該加上李老师，所以结果是（20+1）÷5=4.2≈4（辆）。

生3：不对，4辆车不够，不能保证所有人都上车。

生4：不应该“四舍五入”，应该是（20+1）÷5=4.2≈5（辆）。

师：生4答得很好。所谓“进一法”，指的是在近似数保留整数时，不管小数部分十分位上的数字是几， 都要向整数部分进一。我们在学习数学的过程中，一定要根据实际问题活学活用，这种情境应采用“进一法”，“四舍五入”在这里并不适用。

教学中，教师通过生活实际设计问题，以春游乘坐观光车为切入点引发学生思考。这种以问题为导向的设计可以调动学生思考的主动性，体现了深度设计的情境性。此外，教师采用了循序渐进的教学方式，先是以一个相对简单的问题切入，引发学生思考，在学生初步得出结论后，进一步拓展问题，促进学生深度学习，问题由易到难、层层递进，体现了深度设计的渐进性。最后，教师从具体题目中归纳总结出“进一法”的内涵，把学生单纯的经验转化成知识理论，增强了学生认识的深度，升华了学生的思维。

二、自主思考是深度学习的根本

在传统的小学数学教学中，教师总认为学生认知能力、学习能力和自我管理能力薄弱，因此在课堂的大部分时间一直处于主导地位，这种“填鸭式教学”严重阻碍了学生自主思考能力的发展，压制了学生的表达欲望和探求热情。数学学科具有很强的抽象性和逻辑性，如果使用枯燥乏味的教学模式，将致使师生之间、生生之间缺乏互动，课堂难免会陷入低效和单调。基于上述认识，要实现学生对数学知识的深度学习，教师就必须更新教育理念，通过合作交流、互相沟通、层层设疑、逐步探索等方法，调动学生的学习热情，使学生真正成为学习的小主人，让学生在自由、轻松、愉悦的氛围中探讨、交流、质疑、验证，最终得出结论，实现自主思考。

如， “三角形的概念及特性”教学片段：

师：同学们，在生活中你们一定都见过三角形吧。谁能说一说生活中有哪些三角形或者包含三角形的物体呢？

生1：老师手里的三角板就是三角形的。

生2：埃及金字塔也是三角形的。

生3：我家里的积木也有三角形。

生4：红领巾展开后就是一个三角形。

师：同学们非常善于观察。实际上，我们生活中的三角形还有很多，从规模宏大的金字塔、大型的房屋和桥梁到随处可见的衣架和红领巾，它们都是三角形的。现在，请拿出本子，借助直尺在本子上画一个三角形。（学生画三角形，教师巡视，在这个过程中，教师留意学生不同的画法）

师：同学们都画完了吗？谁能够说一说什么是三角形呢？

生5：三角形是由三条边组成的。

生6：三角形有三个角。

师：现在，男生和女生各为一组，尝试给三角形下一个定义，然后代表发言。

生7（男生）：由三条线段组成的图形就是三角形。

生8（女生）：不对，像              这个图形就不属于三角形。由三条线段组成的封闭图形叫三角形。

生9（男生）：不对，这三条线段不能在同一条直线上。像                                                 这个图形也不是三角形。

师：同学们给的定义越来越严谨了。把大家的想法整合在一起，得出：由不在同一条直线上的三条线段首尾顺次相接组成的封闭图形叫作三角形。

教学中，最突出的亮点在于教师并未照本宣科地告知学生三角形的概念，而是让学生在画一画、说一说中自己发现三角形的内涵，通过各种观点之间的碰撞和冲突，进一步激发学生的自主思考热情。随着思考的不断深入，学生越来越认识到三角形的本质。正是在这种循序渐进、合作探讨、交流沟通中，学生潜移默化地实现了对数学知识的深度学习。教师在整个过程中只是导入者、调控者和总结者，学生才是学习和思考的真正主体。

三、拓展延伸是深度学习的深入

数学學习的拓展延伸是学生在掌握基本概念、原理、公式的基础上，通过整合信息、拓宽思路进一步实现深度思考和深度学习，最终感悟数学方法，培养数学思维。科学而有效的拓展延伸不但能够加深学生对知识的理解，还能够提升学生利用数学思维解决实际问题的能力，使学生养成学数学、做数学、用数学的习惯，培养学生严谨、科学的思维品质。然而，需要注意的是，拓展延伸并非简单地增加教学内容和教学时间，而是实现对数学素材的优化整合和深度加工，在科学性、趣味性和探究性的基础上拓展学生思路，拓宽学生视野，使学生在知识迁移中实现深度学习。

如，“圆柱体的体积”习题教学片段：

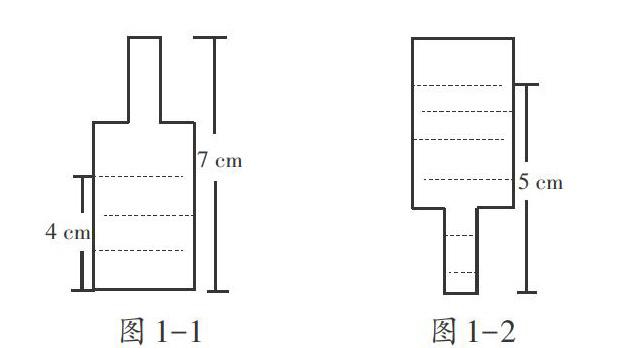
师：如图1-1所示，一个盖着瓶盖的瓶子中装着饮料，瓶子的底面积是5 cm2，那么这个瓶子的容积是多少？

生1：容积的计算公式和体积计算公式一样。

生2：从图1-1看，装着饮料的部分可以求出体积，但是没有装饮料部分是个不规则图形，不能求体积。

师（提示）：那能不能把图1-1中瓶子空白部分的不规则图形转化成规则图形？

生3：我知道了，图1-2的空白部分和图1-1的空白部分体积相等。

师：是的，这道题的关键是图1-2的空白部分的体积正好与图1-1的空白部分的体积相等。若瓶子的体积为V，图1-1装饮料部分的体积为V1，图1-2空白部分的体积为V2，那么V=V1+V2。

教学中，教师对圆柱体体积的基本概念进行了科学的延伸拓展，题目涉及的知识点既源于圆柱体体积，又高于圆柱体体积。在整个过程中，教师把思考的主动权交给了学生，尤其是在生2认为本题无解时，教师并不进行评论，而是稍加提示，让学生质疑、反思，进行深度思考，培养学生的转化思维和解决数学问题的能力。直到生3意识到图1-1的空白部分和图1-2的空白部分相等这一关键信息，教师才开始介入，从整体上对这道题进行梳理和点拨，进而使学生触摸到了问题解决的核心。

总之，小学数学深度学习是一个系统化的工程，它在很大程度上取决于教师的教学活动。深度设计要求教师能从整体上把握教材内容，精心设计教学过程，更加关注学生的学习和发展;自主思考环节要求教师创设适宜的情境，引导学生积极参与学习活动，循序渐进地增加学生思考深度;拓展延伸环节是对教材内容的拓展和延伸，意在使学生进行知识的迁移，发展学生解决问题的能力。这三个环节紧密联系、环环相扣，共同为学生实现数学深度学习提供了可以参考的方法论。

（责编 罗 艳）