一类米氏饱和可逆生化反应模型的Hopf分支
刘晓慧, 郭改慧
(陕西科技大学 文理学院, 陕西 西安 710021)
0 引言
自20世纪60年代末Belousov发现化学反应中的周期振荡现象后,化学与生物化学中的振荡现象受到越来越多学者的关注.Hopf分支作为一种描述周期现象的经典动态分支,对研究物理、生物、化学等系统当参数变化时平衡状态失稳而产生振荡的现象具有重要作用.文献[1]讨论了一类任意阶自催化模型在空间均匀和空间不均匀分布下的Hopf分支及其稳定性.文献[2]研究了一类带有时滞的捕食者-食饵扩散模型,给出了正平衡点的稳定性和Hopf分支的存在性.更多关于稳定性分析和Hopf分支的研究有兴趣的读者可参考文献[3-7]及其中的参考文献.
文献[8]提出一类具有二重饱和度的可逆四分子生化反应模型,研究了系统极限环的存在性、不存在性和惟一性.由文献[9]可知,生化反应中反应速率会对系统产生很大的影响,若反应速率为米氏饱和或二重饱和时,系统可能会出现振荡现象.目前,对二重饱和或米氏饱和可逆生化反应的研究,较多关注的是常微分系统的极限环问题,对常微分系统Hopf分支的研究和带扩散项的扩散系统的讨论较少.所以在文献[8]的基础上,本文考虑一类具有米氏饱和度的可逆四分子生化反应模型
(1)
式(1)中:u,v表示两种反应物的浓度,a,b,c,d均为正常数,主要建立系统(1)Hopf分支的存在性、方向和稳定性,以及对应反应扩散系统正平衡点的稳定性、Turing不稳定性和Hopf分支的存在性等.
基于系统(1)的实际意义,假设u,v均具有非负初始条件.
1 常微分系统的稳定性和Hopf分支
本节,首先讨论系统(1)正平衡点的稳定性,其次分析正平衡点处的Hopf分支.
易知,d≤a时,系统(1)无正平衡点;当d>a时,系统(1)存在惟一的正平衡点(u*,v*),其中
系统(1)在(u*,v*)处的Jacobi矩阵为
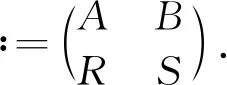
显然A<0,R>0.注意到
假设条件
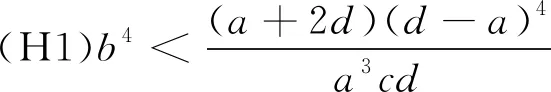
成立.令
以下均假设条件(H1)成立.
定理1设d>a.
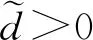
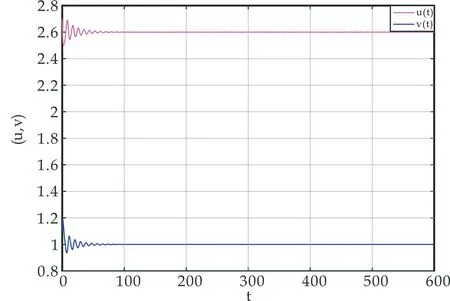
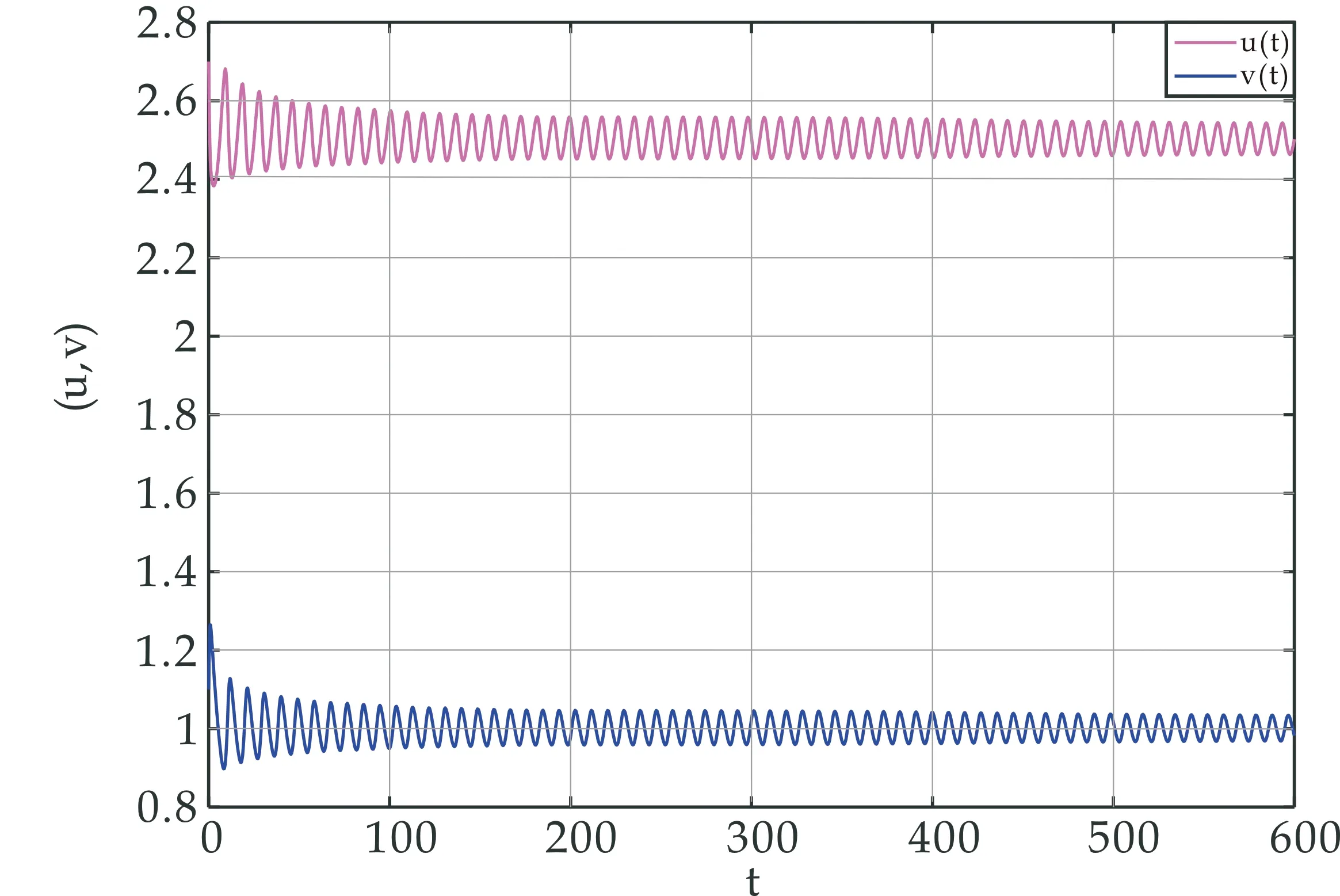
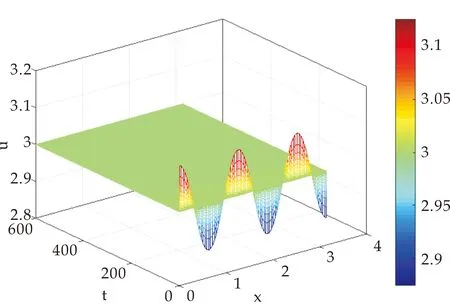
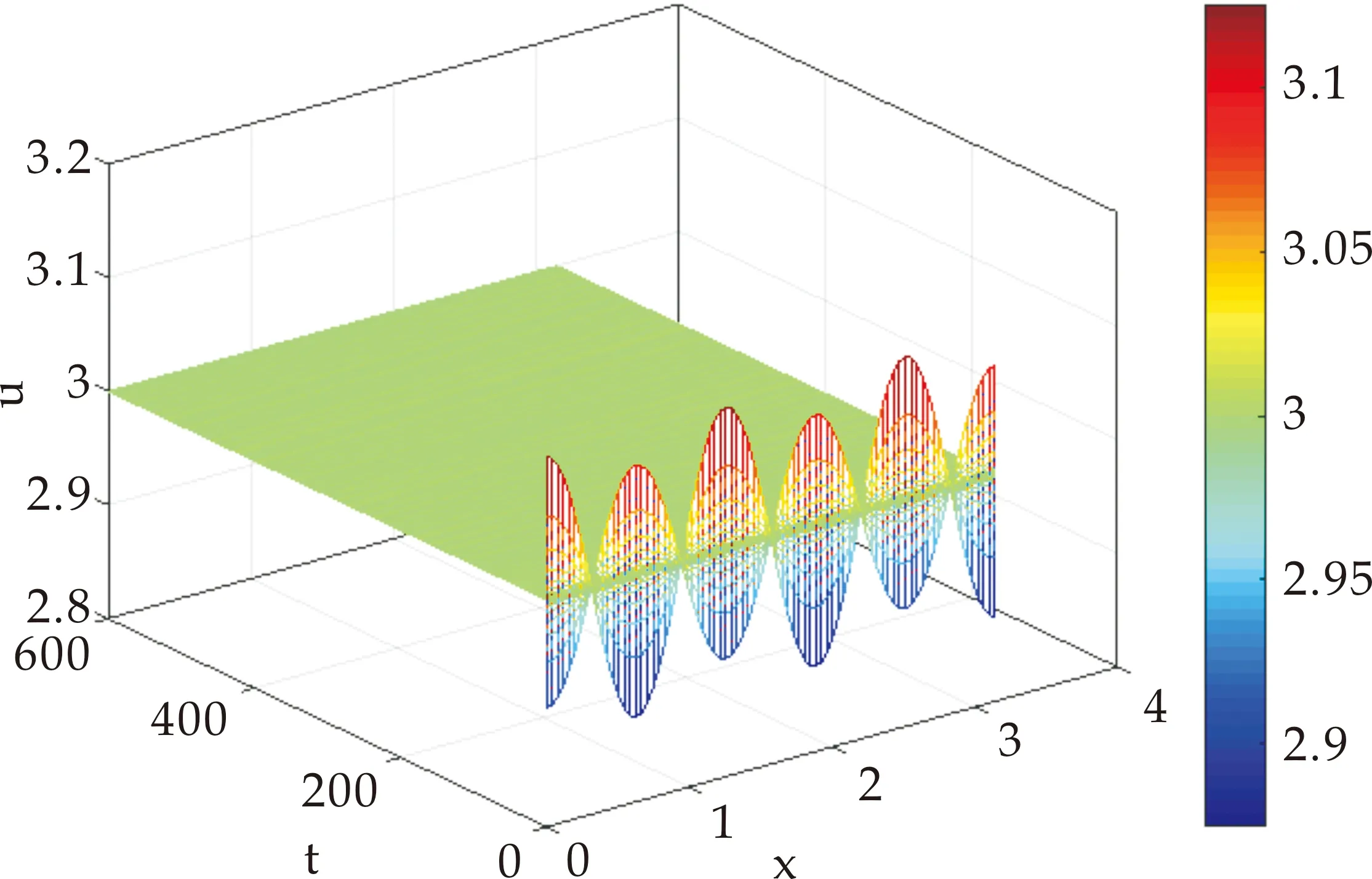
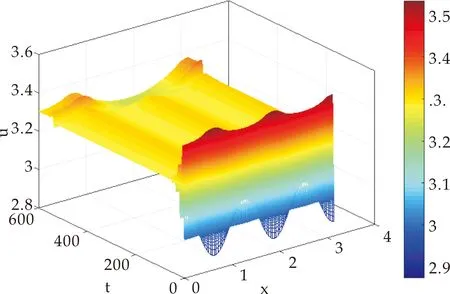
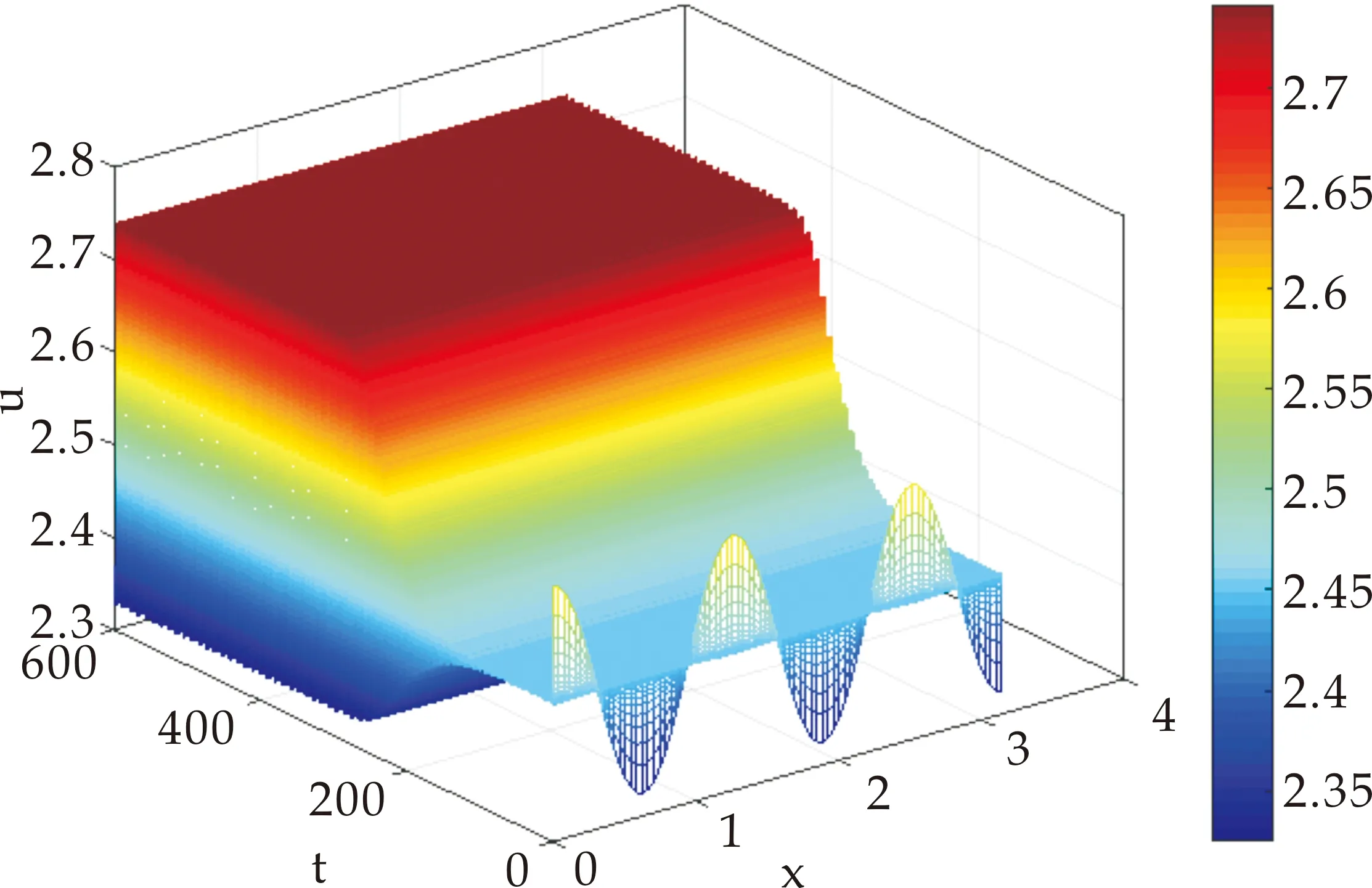
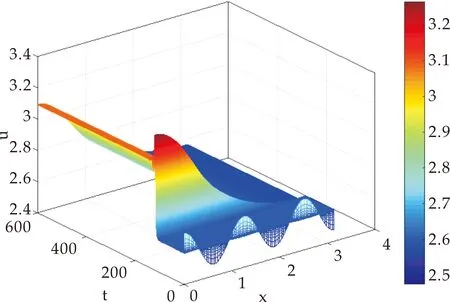
(i)若0 (ii)若c>c0,则系统(1)的惟一正平衡点(u*,v*)局部渐近稳定; (iii)若c=c0,则系统(1)在正平衡点(u*,v*)处产生Hopf分支,且该Hopf分支为次临界方向,周期闭轨渐近稳定. 证明:(i)当0 (ii)当c>c0时,T<0又因D>0,故J的特征值实部均小于0,此时正平衡点(u*,v*)局部渐近稳定; (iii)令λ=α(c)±iβ(c)为J的一对共轭复特征根,其中 (2) 重写系统(2)为 (3) 其中 F1(u,v,c)=-a1uv+a2v2-a3uv2+a4v3+ O(|u||v|3,|v|4), F2(u,v,c)=a1uv+a5v2+a3uv2+a6v3+ O(|u||v|3,|v|4). 这里 a3=3v*,a4=-u*+4cv*, 定义矩阵 其中 显然,当c=c0时,P是可逆的,即 易知 当c=c0时, 其中 G1(x,y,c)=F1(x,Mx+Ny,c), 通过计算可得G1(x,y,c)和G2(x,y,c)在(0,0,c0)处的各阶偏导数为 下面通过判断q(c0)的符号给出周期解的方向和稳定性[10],其中 由于d>a,将G1(x,y,c)和G2(x,y,c)在(0,0,c0)处的各阶偏导数代入q(c0)计算可得 q(c0)= 注意到α′(c0)<0,由Poincare-Andronov-Hopf分支定理[11]知,系统(1)在正平衡点(u*,v*)处产生Hopf分支,且该Hopf分支为次临界方向,周期闭轨渐近稳定.证毕. 本节讨论具有米氏饱和度的可逆四分子生化反应扩散系统 (4) 其中Ω为n维欧式空间的有界开集,并且具有光滑边界∂Ω,γ表示∂Ω上单位外法向量,d1,d2分别代表两种反应物的扩散系数,均为正常数,Δ为拉普拉斯算子. 定义实Sobolev空间 X={(u,v)∈(H2(Ω))2:uγ=vγ=0,x∈∂Ω}, 并且定义X的复延拓空间 XC=X⊕iX={x1+ix2|x1,x2∈X}. 系统(4)在(u*,v*)处的线性化算子为 在齐次Neumann边界条件下,算子-Δ的特征值满足 0=λ0<λ1<λ2<λ3<…, 且φk(x)(k∈N)为对应λk的特征函数.令 为L对应特征值μ的特征函数,即 L(φ,ψ)T=μ(φ,ψ)T. 经计算 其中 Lk= 显然L的特征值可由Lk的特征值给出.设Lk的特征方程为 μ2-Tkμ+Dk=0,k=0,1,2,…, 其中 Tk=T-(d1+d2)λk, 当0 下面考虑系统(4)当c0 当0 注意到二次函数 的判别式为 因此f(z)=0存在两个实根 如果z1 定理2设d>a. (i)当0 (ii)当c0 当c0 存在两个正实根 其中 注意到 λ+(d1,d2)= 令 则 定义 Γ1={λ|λ≥0,λ-(d1,d2)<λ<λ+(d1,d2)}, Γ2={λ0,λ1,λ2,λ3,λ4,…}. 要使不等式0 固定d2且令d1→∞,则 从而对所有的d1>0,有 由上述分析得到如下结论. 定理3设d>a.当c0 (5) 则对于固定的d2>0和所有的d1>0,系统(4)的正平衡点(u*,v*)局部渐近稳定. 证明:如果(5)式成立,那么 Γ1∩Γ2=Ø. 此时,对所有的k∈N,Dk>0且Tk<0,故系统(4)的正平衡点(u*,v*)局部渐近稳定.证毕. 固定d1且令d2→0,则 定理5设d>a.令 证明:若c=c0,则T0=0且D0>0.由于λk>0(k≥1)且d1,d2>0,于是对所有的k≥1,有Tk(c0)<0.经计算 根据Poincare-Andronov-Hopf分支定理[11]可知,当c=c0时,系统(4)在(u*,v*,c0)处产生Hopf分支.证毕. 本节,给出一些具体的数值实例,对所得的理论结果进行验证补充.取a=1,b=1,d=2,则c0=1.5. 对系统(1),取c=1.6>c0,此时T<0,由定理1(ii)可知正平衡点(u*,v*)局部渐近稳定,如图1所示. (a)时间图 取c=1.5=c0,由定理1(iii)知在(u*,v*)附近系统(1)存在次临界的Hopf分支,如图2所示.均取初值(u(0),v(0))=(2.7,1.1). (a)时间图 对扩散系统(4),Ω取一维空间(0,π).当c=2时,z1=0.227.如果取d1=1,d2=0.3,那么d1,d2满足条件d2/d1>z1,因此,由定理2(ii)可知系统(4)的正平衡点(u*,v*)局部渐近稳定,如图3所示. (a)u的时空分布 若取d1=60,d2=3,则d1,d2满足条件0 若取d1=1,d2=0.006,则d1,d2满足条件0 如果取c=1.45,d1=1,d2=0.3,那么由定理5可知,系统(4)在正平衡点(u*,v*)处出现稳定的Hopf分支周期解,如图6所示. 若取c=1.6,d1=1.22,d2=0.1,系统(4)产生稳态分支,如图7所示.初始值均取(u0,v0)=(2.7+0.125 4cos5x,1.1+0.125 4cos5x). (a)u的时空分布 (a)u的时空分布 (a)u的时空分布 (a)u的时空分布 本文在齐次Neumann边界条件下,以一类具有米氏饱和度的可逆四分子生化反应模型为研究对象.首先分析了正平衡点的局部稳定性和Hopf分支的存在性及稳定性; 然后讨论了对应扩散系统正平衡点的稳定性和Turing不稳定性.特别是扩散系统,当c0
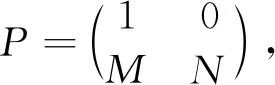
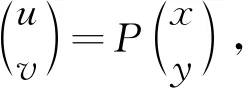
2 反应扩散系统的Turing不稳定性和Hopf分支
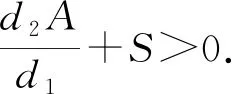

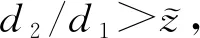
3 数值模拟
4 结论

