基于WCA的阵列天线方向图综合算法研究及实现
仇 亮, 王云秀*, 郑 霞, 樊 琴, 段寅龙, 贾瑞林
(1.西华师范大学 电子信息工程学院, 四川 南充 637009; 2.重庆三峡学院 电子与信息工程学院, 重庆 404000)
0 引言
在地球表面热能和太阳能的作用下,地球上的水不断被蒸发成为水蒸气,进入大气.水蒸气遇冷又凝聚成水滴,在地球重力的作用下,以降水的形式落到地面,这个周而复始的过程,称为水循环.在地球表面的水进行循环过程中,一部分通过渗透作用汇集到地下河沟、湖泊等,另一部分因为表面水流的重力运动,水流自行从高处流向低处,形成更大的溪流,再经过不同溪流的汇合,进而流向河流和大海.这种现象类似于寻优算法求解目标最优解的过程.
根据上述水循环现象,2012 年Eskandar H等[1]通过模仿自然界中的水循环过程,提出了最早的水循环算法(WCA),经与其它常见的优化算法比较,发现水循环算法具有运行速度快、收敛精度高的特点;次年,Saddlah等[2]再次利用水循环算法优化离散和连续变量衍架结构的尺寸;2014年,根据Pareto Optimality理论[3],章纯等[4,5]将水循环算法用于验证空间桁架结构优化设计问题的可行性及有效性,最终测试结果表明:相对于群搜索算法(GSO)[6],启发式粒子群优化算法(HPSO)[7]等优化算法,WCA能够提供更快的收敛速度,收敛结果也更好; 2015年,Sadollah等[8]在水循环算法的基础上进行了改进,提出了一种带有蒸发系数的水循环算法,使得算法过程更完整.之后,水循环算法得到了更广泛的应用[9]:2016年,广西民族大学的乔石磊[10]提出了一种基于复数编码的水循环算法(CWCA),这种编码方式扩展了种群个体的信息量,提高了算法的多样性;2018年,郭佩刚[11]将水循环算法应用于物流选址规划结构框架;2019年,陕西师范大学的郭洁皓[12]将WCA与基本粒子群算法结合,改善了算法性能.
另一方面,物联网技术的高速发展对研发设计出更高品质的阵列天线提出了新的要求,即阵列天线需要综合得出一些特殊形状的波束[13],比如方向图要求宽波束的广播、移动网中的高增益窄波束方向图,又或者常见的某些雷达和低噪声系统,其方向图要求副瓣强度随着角度偏离主瓣而逐次递减.伴随阵列天线方向图综合研究取得巨大的进展的同时,越来越多的优化算法也应用于方向图综合问题中,且取得了较大的进展,但是当前寻找到一种优化速度更快、收敛精度更高、稳定性更强的综合算法在阵列天线方向图综合领域仍然是一个热点.
本文将WCA应用到阵列天线方向图综合中,同时与遗传算法方向图综合结果比较,发现WCA每次都能找到目标最优解,且在收敛精度、优化速度上远远胜过遗传算法,证明了WCA适用于阵列天线方向图综合问题.
1 水循环算法实现步骤
与其他根据自然现象提出的启发式算法一样,水循环算法首先要建立一个初始种群,我们假定全部的降雨个体构成了水循环算法的总体.因此在最开始,算法首先会根据个体的适合度值划分为三个层次,定义最好的层次是海洋,较好层次的是河流,剩下的个体都作为溪流,然后算法开始进入优化的迭代过程,把优化迭代过程分为三个过程,第一个过程是小溪流向河流,第二个过程是河流流向海洋,最后是降雨过程.随着算法更新迭代过程,每次更新后,三个不同适应度值的个体将要被重新划分,然后再次执行优化迭代步骤,进行下一轮更新迭代过程,直到找到最终的海洋,即算法寻优到目标最优解,整个算法优化过程结束.
下面列出实现水循环算法的详细步骤:
Step1设置水循环算法的初始参数.初始种群Npop,河流加上大海的总数目为Nsr,优化精度dmax,最大迭代次数max_ it.
Step2产生初始种群,根据适应度值划分大海、河流、溪流,则溪流数目如公式(1)所示:
Nstream=Npop-Nsr
(1)
适应度函数的转换关系如公式(2)所示:
Cn=Costn-CostNsr+1,n=1,2,3,…,Nsr
(2)
适应度函数值越小,意味着越接近最优解,其需要连接的河流或者溪流的数目越多,也就是Cn越大,因此Cn和Costn是相反的关系.
流入指定河流或者海洋的溪流数目见公式(3):
n=1,2,3,…,Nsr
(3)
适应度值越好,也就是河流或者大海的流量越大,流入该河流或者海洋的溪流数目就越多.
Step3溪流流入河流和大海,更新溪流位置,当溪流的位置优于河流和大海时,交换各自位置.下式中C>1,一般选择 2, rand为0到1之间均匀分布的随机数.
其位置更新公式如下:
(1)溪流流向河流位置更新如公式(4):
Xstream(t+1)=Xstream(t)+rand×C×
(XRiver(t+1)-Xstream(t))
(4)
(2)溪流流向大海位置更新如公式(5):
Xstream(t+1)=Xstream(t)+rand×C×
(XSea(t+1)-Xstream(t))
(5)
Step4河流流入大海,更新河流位置,当河流位置优于大海时,交换彼此位置.因此河流流向大海位置更新为公式(6):
XRiver(t+1)=XRiver(t)+rand×C×
(XSea(t+1)-XRiver(t))
(6)
Step5判断是否满足蒸发条件,如果满足则执行相应的降雨,其蒸发条件如公式(7)、(8)所示:
(7)
(8)
其中,NS1为流入大海的溪流数目,dmax是个很小的数,接近于0,当dmax太大时,河流或者溪流距离最优解大海相对较大时就会进行蒸发,导致搜索空间变大;当dmax太小时,河流或者溪流距离最优解海洋非常小时才会进行蒸发,即在海洋附近搜索.dmax控制海洋位置附近的搜索区域强度且随着迭代地进行自适应减小,通常一开始取dmax=1e-16,如果满足降雨条件公式(9):
fori=2:Nsr-1
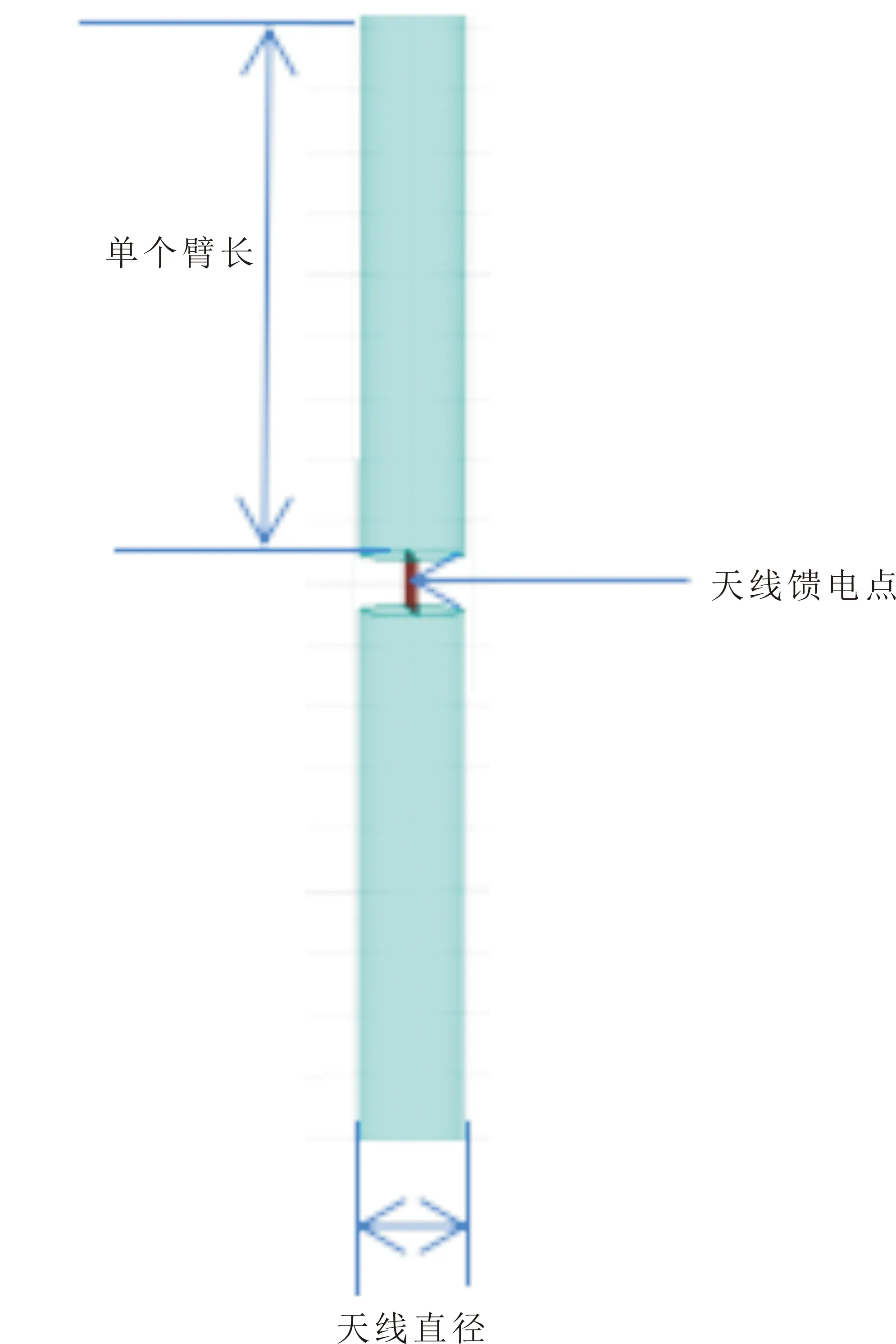
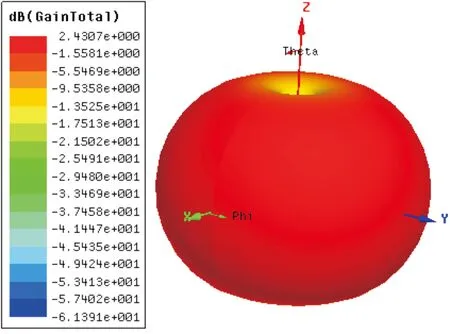
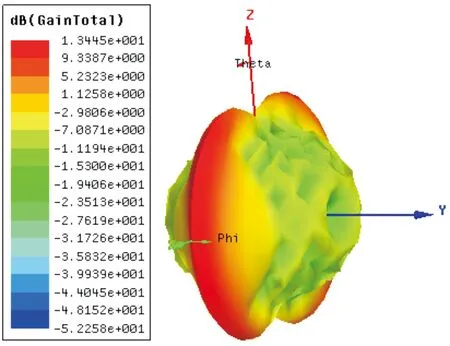
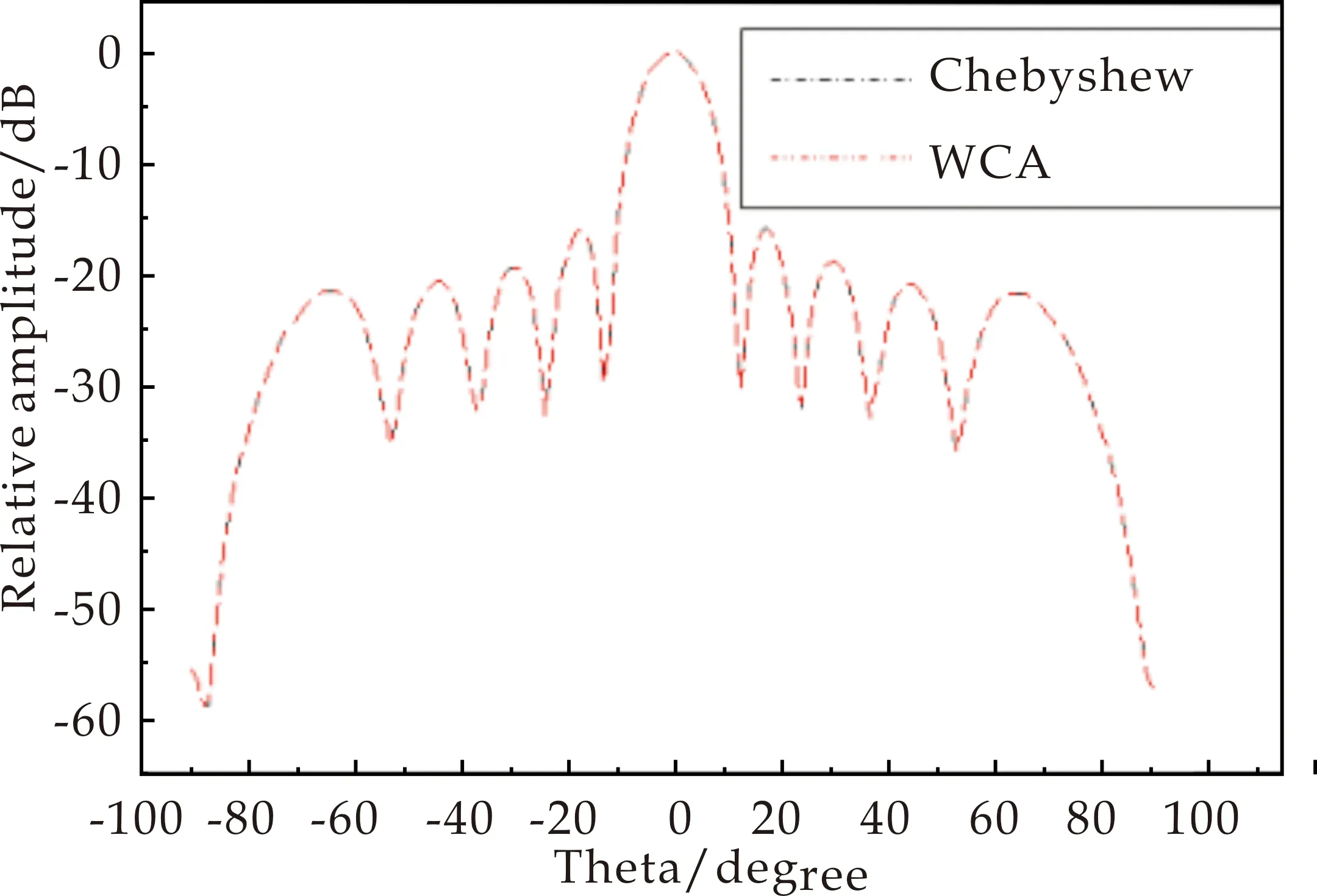
if(e(-k/max_it) (9) k为当前迭代次数,max_it为最大迭代次数,则执行降雨,具体操作如下: 如果条件满足公式(7),则在问题空间内执行降雨操作,具体的做法如公式(10): (10) 同样地,如果条件满足公式(8),则在大海附近执行降雨操作,具体的操作如公式(11): (11) 其中,LB和UB分别为问题空间的下界和上界,参数μ决定着新产生个体的分散程度,表示在海洋周围的搜索范围,这里取为0.1.从以上公式可以看出,降雨分为两种,一种降雨将在问题空间内产生随机个体,以增加种群个体的多样性,另一种降雨过程则在海洋附近产生降雨,以便于在当前最优值附近继续寻找其他较优值.randn(1,N) 是一行N列的符合正态分布随机数矩阵. Step6根据公式(12)调整dmax: (12) Step7判断是否满足最大迭代次数,如果满足最大迭代次数,算法结束并返回最优解;如果不满足最大迭代次数,算法当继续优化,进入Step 3. 以上是完整的实现水循环算法的步骤,为了测试并检验水循环算法(WCA)的先进性、有效性和普遍适用性,测试过程中选择部分典型的标准检验函数[14,15]对水循环算法进行检验.为保证该算法的有效性,测试过程中采用控制变量的办法进行,即通过控制测试函数维度和种群数量的办法进行算法优化测试. 遗传算法的使用已经较为成熟[16,17],水循环算法目前在部分函数优化中得到了应用,在这些问题的优化过程中,水循环算法皆显示出了优秀的随机搜索能力和稳定性.在阵列天线方向图综合领域,水循环算法还未得到广泛应用,本章将对WCA算法进行测试验证,并与遗传算法优化测试结果进行对比. 下面测试的两个函数全局最优解近似在函数值等于零处,仿真实验利用GA和WCA对函数最优解进行寻优测试,GA和WCA的参数设置如下所示: GA:问题的上下限[-10,10],种群数量NIND=200,维度n=2、5、10、50,最大迭代次数MAXGEN=1 000,变量的二进制位数PRECI=20. WCA:问题的上下限[-10,10],种群数量Npop=200,维度n=2、5、10、50,最大迭代次数MAXGEN=1 000,大海和溪流的数量和Nsr=4,蒸发条件常数dmax=1e-5. 将GA和WCA两种算法在测试函数上进行测试,选定计算时间、最佳适应度值、收敛曲线三种参数来验证算法性能.为了测试图像更直观,对最优值取对数表示,测试函数表见表1所示. 表1 两个经典的单峰/多峰测试函数 2.2.1 函数图像 Sphere函数是一个球面单峰函数,该函数极难找到全局最优解; Rastrigin函数图像有点类似单峰Sphere函数,其最优解存在多个局部的峰底.具体如图1所示. (a)Sphere函数 2.2.2 仿真结果 将GA算法和WCA算法分别用于单峰/多峰函数的寻优测试,寻优最佳值为0,下面列出了两种算法各自用于优化的收敛时间和最佳适应度对比(MAXGEN=1 000,种群数N=200).适应度值测试结果见图2和图3所示.根据图2、图3可以观察到,WCA的收敛精度远远高于GA,GA更容易受到种群数不足的影响,导致其收敛精度不高,收敛速度两者各有优劣. (a)GA寻优收敛曲线 (a) GA寻优收敛曲线 优化时间、收敛精度测试结果见表2和表3所示.根据表2可以看出,随着维度的增加,利用WCA优化测试的单峰和多峰函数优化时间都远远低于GA优化时间;同时通过表3中的数据可以更直观地看出WCA收敛精度远远高于GA. 表2 单峰/多峰测试函数(种群数N=200、 表3 单峰/多峰测试函数(种群数N=200、MAXGEN=1 000、收敛维度n=2、5、10、50)优化的最佳适应度 根据测试结果可知,WCA的收敛精度和优化时间皆优于GA.从WCA的寻优机制来说,在解决实际问题时,WCA运用间接寻找最优解的方法,排除最优解(大海),将次优解(河流)作为引导,引导群体中的其他个体(溪流)流到最好的位置,这个过程减少了算法在不恰当区域的搜索,提高了算法寻优的效率和准确性,同时其蒸发和降雨过程有效地防止算法过早陷入局部最优解;而GA在寻优测试时,普遍受到维度和种群数数量不足的影响,GA算法因为种群数不足而过早收敛,或者直接寻优到最优解,导致其收敛精度不高.相比之下,WCA比GA更优越. 测试过程中,WCA的可调参数更少,计算速度快,收敛精度高,因此可以考虑将WCA应用到解决复杂的优化问题中,提高优化效率. 3.1.1 Chebyshew综合方法仿真测试 设计一个阵元数N=31,阵元间距d=λ/2,综合一个等副瓣电平为SLL= -20 dB的Chebyshew直线阵列的方向图[18,19]. 图4为Chebyshew综合法得到的副瓣电平为-20 dB的方向图综合结果(利用Python语言编程).为使方向图综合结果对比更明显,引入了均匀激励(In=1 )作为对比(图中红色线表示).从图4可以看到,运用Chebyshew综合方法能够满足方向图对于副瓣电平的要求,采用均匀激励综合的方向图彻底偏离了主瓣且副瓣电平不满足设计要求. 图4 Chebyshew激励和均匀激励方向图 3.1.2 WCA、GA优化后的Chebyshew型天线阵方向图综合 测试目标:利用理想点源综合一个阵元数目为N=31的均匀直线阵列低副瓣方向图,阵元间距为半个波长,副瓣电平SLL=-30 dB.激励电流的相位为0(侧射阵),激励幅度In的范围为[0,1],加权系数α为1,分别用GA和WCA对电流In的值进行优化,GA和WCA的参数设置如下: GA:问题的上下限[0,1],种群数量NIND=50最大迭代次数MAXGEN=500,变量的二进制位数PRECI=20. WCA:问题的上下限[0,1],种群数量Npop=50,最大迭代次数MAXGEN=500,大海和溪流的数量和Nsr=4,蒸发条件常数dmax=1e-5.优化结果分别为:表4是31阶Chebyshew型阵列单元激励值;表5是利用GA、WCA优化后的各单元激励值,因阵列单元对称,仅给出一半激励;表6是GA、WCA优化31阶方向图所用时间. 表4 Chebyshew型阵列单元激励值(N=31) 表5 GA、WCA优化后的各单元激励值(N=31) 表6 GA、WCA优化所用时间(单位:s) 根据方向图综合测试结果可以明显发现,表5中WCA优化后的激励值远远接近表4中作为参考标准的Chebyshew型阵列单元激励值.表6中WCA优化时间远远低于GA优化时间.实际方向图的综合结果如图5所示. 图5 GA、WCA优化后的切比雪夫直线阵(阵元数目N=31,副瓣SLL=-30 dB) 根据图5的方向图综合结果可以看出,利用WCA和GA优化过的阵列方向图均与切比雪夫型方向图吻合,但在优化时间、收敛精度上,GA远远不如WCA. 3.2.1 傅里叶综合方法仿真测试 用阵列阶数N=11综合一个预期方向图的值在 和 之间,测试实验要求如公式(12)所示: (12) 分析得出,公式(12)方向图关于θ=π/2对称.同时设定了期望方向图作为参考,图6为阵列阶数N=11的综合结果,观察发现傅里叶变换综合法[20]更接近期望的方向图. 图6 傅里叶综合与均匀激励综合预期方向图 3.2.2 WCA、GA优化后的傅里叶型天线阵方向图综合 测试目标:利用理想点源综合一个阵元数目为N=19的均匀直线阵列,使其形成如公式(12)期望的方向图. 阵元间距为半个波长.激励电流的相位为0(侧射阵),激励幅度In的范围为[0,1],加权系数α为1,GA和WCA的参数设置如下: GA:问题的上下限[0,1],种群数量NIND=100,最大迭代次数MAXGEN=500,变量的二进制位数PRECI=20. WCA:问题的上下限[0,1],种群数量Npop=100,最大迭代次数MAXGEN=500,大海和溪流的数量和Nsr=4,蒸发条件常数dmax=1e-5.实验测试结果为:表7是19阶傅里叶型阵列单元激励值;表8是利用GA、WCA优化后的各单元激励值;表9是GA、WCA优化19阶傅里叶型方向图所用时间. 表7 傅里叶型阵列单元激励值(N=19) 表8 GA、WCA优化后的各单元激励值(N=19) 表9 GA、WCA优化所用时间(单位:s) 和3.2节的测试方法一样,根据方向图综合结果同样可以发现:表8中WCA优化后的激励值远远接近表7中作为参考标准的傅里叶型阵列单元激励值;表9中WCA优化时间远远低于GA优化时间.实际方向图综合结果图见图7所示. 图7 GA、WCA优化后的傅里叶直线阵(阵元数目N=19) 根据图7所示的 GA、WCA优化后的19阶傅里叶方向图综合对比,可以观察出WCA和GA方向图均与傅里叶型方向图吻合,但在整个优化过程中,WCA在收敛精度方面远远高于GA、在优化时间上也远远快于GA,结合两次测试结果,证明WCA适用于阵列天线方向图综合问题,同时其收敛精度和优化时间远远优于GA. 3.3.1 自由空间单个偶极子天线设计与仿真 本小节将使用最常见的半波偶极子天线单元[21]进行组阵,在进行组阵之前,将对用以组阵的单个偶极子天线进行仿真测试.测试所用单个偶极子天线的工作频率f=3 GHz、工作波长λ=100 mm .根据电磁长度换算关系计算得出偶极子天线的长度,并在HFSS电磁仿真软件中建立偶极子天线仿真模型,具体可见图8所示;经过HFSS电磁软件仿真后优化得到的单个偶极子天线参数如表10所示.偶极子天线具体变量名和参数为:λ,工作波长;Length,偶极子天线长度;Feed_gap,馈电端口总长度; Feed_radius,馈电半径;Single_length,天线半个臂长度. 图8 偶极子天线仿真模型 表10 单个偶极子天线参数 在HFSS中建模仿真后,从图9、图10可以看出,该半波偶极子天线的三维增益最大已经达到2.44 dB,其反射系数S11在中心频率f=3 GHz处最低达到了-15 dB左右,基本满足对天线组阵的要求.最后,从图11可以看出,该偶极子天线满足一定的全向电磁辐射特性[22],综合考虑下可以将该半波偶极子天线用于阵列天线组阵. 图9 半波偶极子天线三维增益方向图 图10 半波偶极子天线的S11图 图11 半波偶极子天线的xoz面增益方向图 3.3.2 10阶偶极子阵列天线方向图仿真 构造1*10的Chebyshew型直线阵[23],其中阵元和激励幅度、激励相位等都关于坐标原点对称,阵元间距d=0.5λ,要求副瓣电平SLL< -20 dB阵列天线模型(10阶)如图12所示. 图12 10阶半波偶极子阵列天线模型(沿xoy面设置阵列) 将前面测试优化过后的Chebyshew型直线阵的激励幅度和激励相位代入HFSS[24]仿真测试模型中,同时比较优化的结果和在HFSS模型中实际仿真的差异.根据前面设计的半波偶极子结构,利用HFSS仿真得到的Chebyshew直线阵S11图[25]、3D极坐标图,分别如图13、14所示. 图13 10元Chebyshew直线阵S11图 图14 10元Chebyshew直线阵3D极坐标图 根据上述实验测试结果可以明显观察到:HFSS中构造的Chebyshew直线阵的S11参数低于-13 dB,满足设计要求;组阵后的阵列天线增益放大倍数略有降低,原因可能是阵元间相互辐射影响导致,本文仅为测试WCA算法的优化特性,因此不对此问题做深入探究;根据仿真对比图15观察发现利用WCA算法优化后的切比雪夫直线阵结果与在HFSS中仿真结果基本一致,副瓣电平有微小波动误差,不影响实验的可靠性.因此,证明了利用WCA算法在优化阵列天线方向图综合问题中的可行性和准确性. 图15 HFSS中利用WCA优化后的Chebyshew直线阵与Chebyshew直线阵方向图综合仿真对比图 本文主要内容是对GA和WCA应用到单峰/多峰函数以及阵列天线方向图综合问题上的优化效果对比测试,针对WCA自身的寻优机制和优化特点对其进行了一定的测试和对比;采用了1个比较典型的单峰测试函数、1个多峰测试函数,结果显示WCA均能找到最优解,且在收敛精度、优化时间上远远优于GA,说明了WCA可以应用到大型阵列优化过程问题中且性能超过GA;将WCA应用到阵列线阵方向图综合中,例如Chebyshew型、傅里叶型方向图综合问题以及在HFSS中组阵仿真,WCA算法均能解决实际问题的方向图综合,这正说明了WCA的准确性和高效性,再一次说明了WCA收敛精度高、优化时间短的特点.2 WCA、GA仿真测试结果与对比分析
2.1 GA和WCA优化设置参数

2.2 单峰/多峰函数仿真测试结果

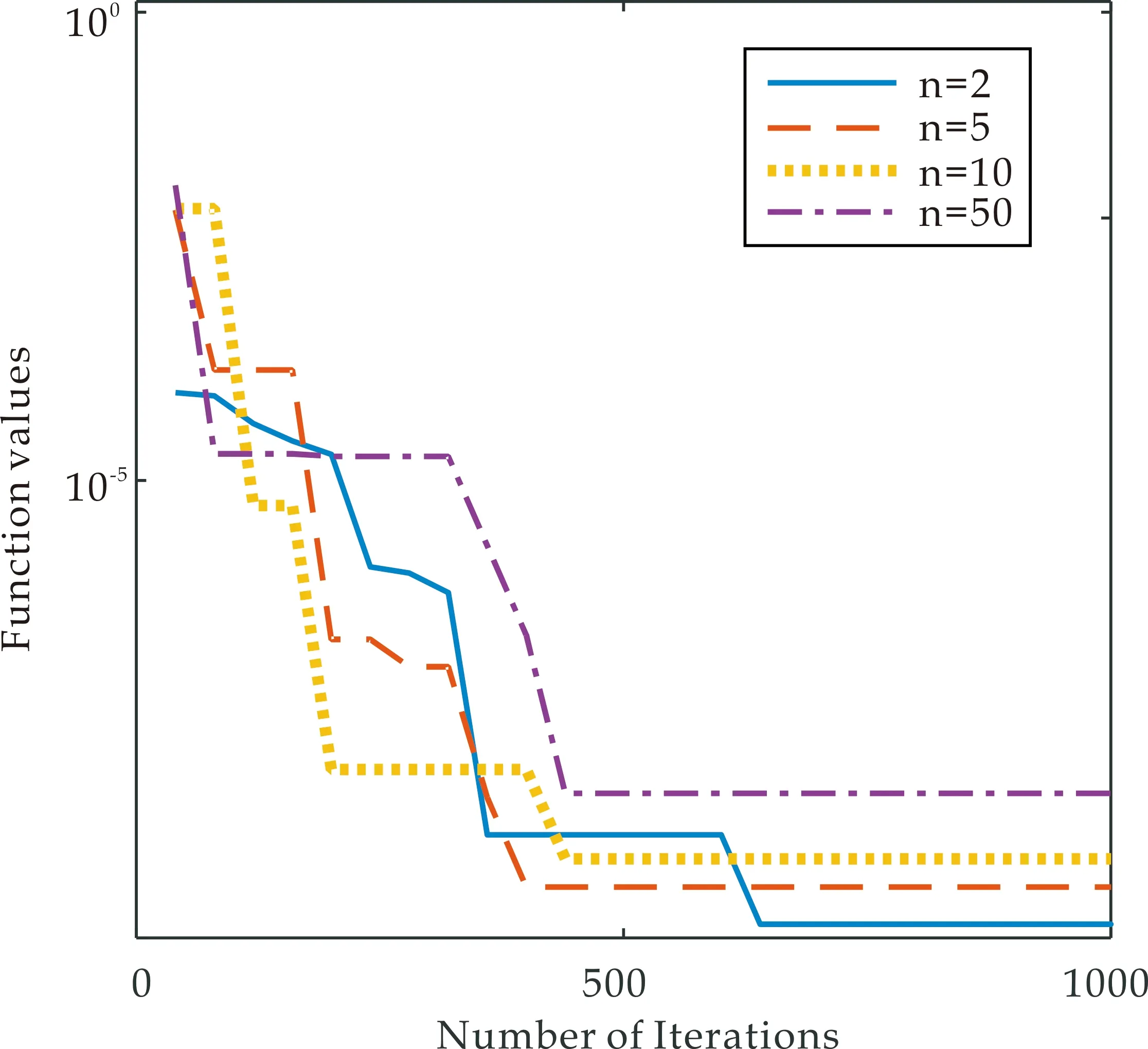
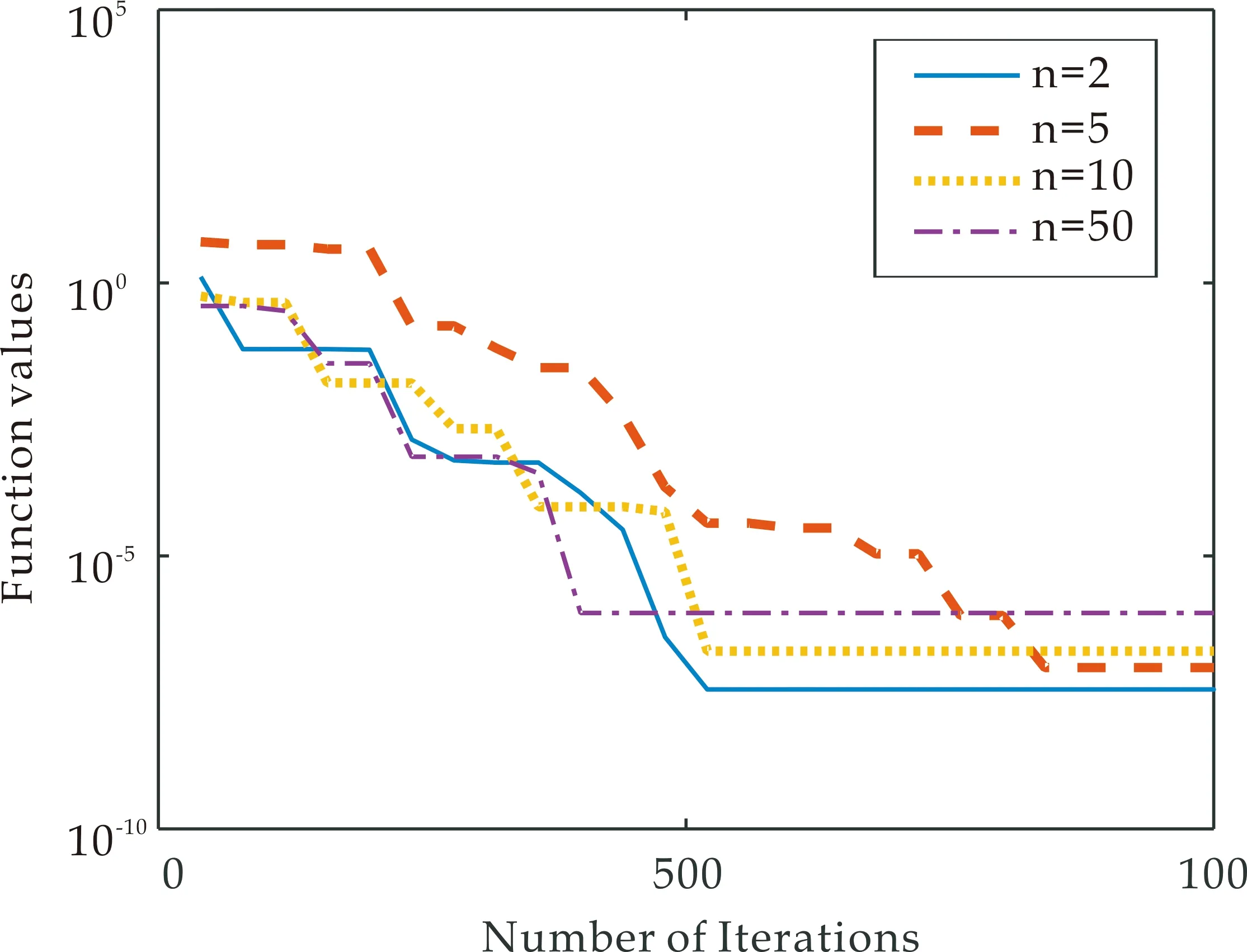
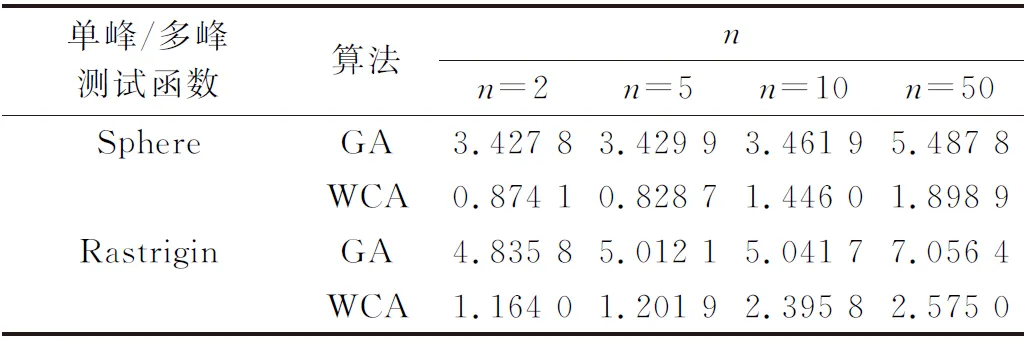
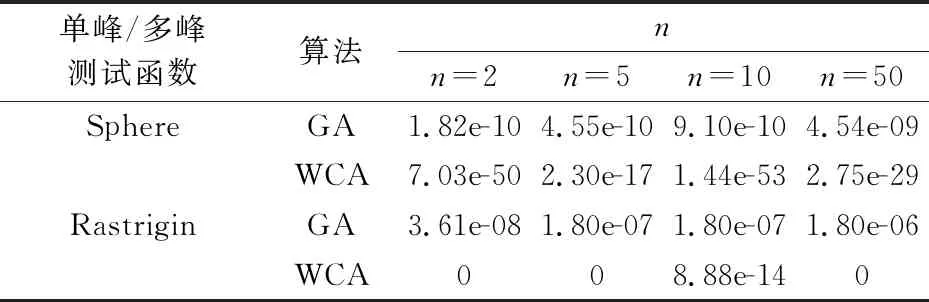
3 阵列天线方向图综合
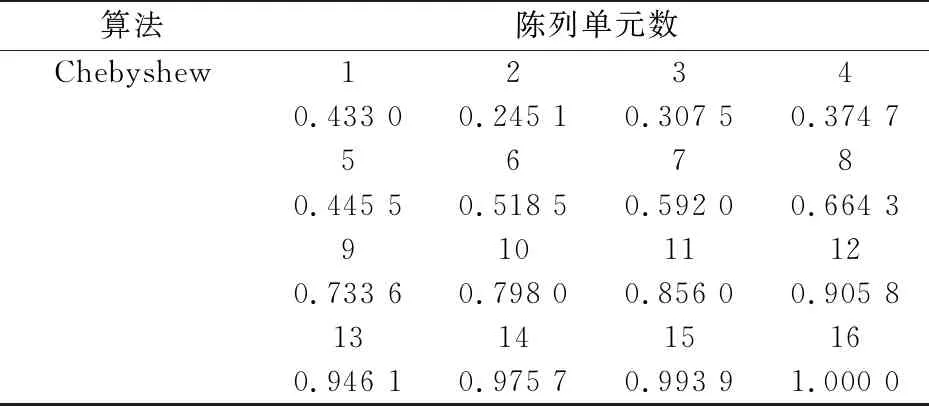
3.1 Chebyshew型阵列天线方向图综合



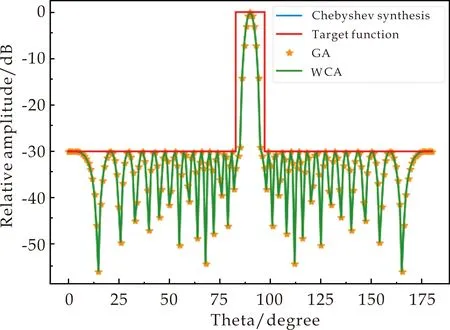
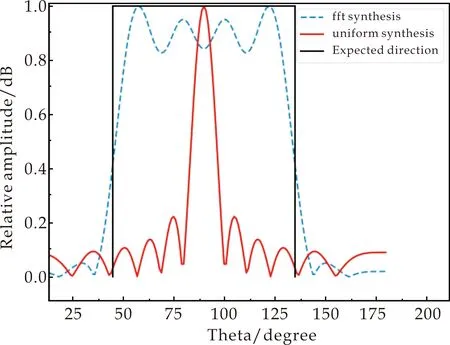
3.2 傅里叶型阵列天线方向图综合
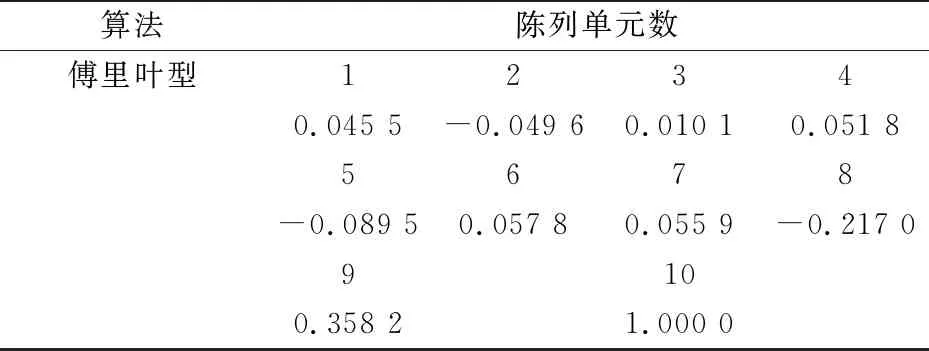



3.3 自由空间阵列天线直线阵HFSS模型仿真





4 结论

