新疆吉木萨尔页岩油藏压裂水平井压裂簇数优化研究

谢建勇， 石璐铭， 吴承美， 陈昊枢，许 锋，张兴娇， 张金风， 孙海波

(1.中国石油新疆油田分公司 准东采油厂， 新疆 阜康 831511； 2.中国石油大学 (北京) 油气资源与探测国家重点实验室， 北京 102249)

0 引言

近年来，随着北美页岩油开采的巨大成功，全球的石油天然气勘探开发越来越关注页岩油[1-5].页岩油藏原始渗透率极低，自然条件下无经济产能，实践表明水平井大型水力压裂是高效开发页岩油藏的最有效手段.

目前，已有国内外学者对多段压裂水平井渗流理论开展了一些相关的研究工作.1985年，Giger[6]首次对压裂水平井的渗流问题进行研究，并指出水平井是开发非均质性油藏的一种好方法.1995年，Horne等[7]建立了多段压裂水平井渗流物理数学模型，利用叠加原理，对模型进行了求解，并分析了多条裂缝间的干扰效应，同时划分了多段压裂水平井渗流流动阶段.1996年，Chen等[8]在Horne的研究基础上，建立了在Laplace空间下矩形油藏中多段压裂水平井的压力动态.同年，李笑萍[9]建立了均质油藏多段压裂水平井渗流模型并得到模型理论特征曲线.2009年，樊冬艳等[10]基于源函数及Newman乘积原理，建立并求解了考虑裂缝倾角的无限导流封闭油藏多段度裂水平井渗流模型，并绘制了试井样版曲线.2000年，陈伟等[11]建立了考虑井筒储集效应的表皮效应、裂缝方位等因素的均质和裂缝性油藏内多段压裂水平井渗流模型，并计算得到理论特征曲线.2010年，Luo等[12]通过数值流线模拟的方法针对无限大地层压裂水平井进行了模拟，利用双对数导数速率曲线分析了多段压裂水平井的流动情况.2013年，姚军等[13]考虑双重介质模型针对顶底封闭四周无限大油藏的点源解，通过计算得到了不同边界条件下油藏中一条不完全穿透地层裂缝压降解.2014年，苏玉亮等[14]研究了多段压裂水平井复合流动模型，并分析了各参数对产量的影响.2018年，陈昊枢等[15]和陈志明等[16]基于不稳定渗流理论，建立了页岩油藏多段压裂水平井渗流模型，并提出了页岩油藏压裂水平井试井分析方法，2020年，梁成钢等[17]针对新疆吉木萨尔致密油藏井距优化的问题，建立了数值模型得到了该地区最优井距的理论值，并对产量进行了预测.

总之，通过国内外学者研究，多段压裂水平井渗流理论方面取得了一系列进展.然而，目前鲜有关于页岩油藏压裂水平井裂缝簇数优化研究的报道.针对这一问题，利用不稳定渗流理论建立了多段压裂水平井多井数值模型，在储量动用充分的原则，提出了一套页岩油藏多段压裂水平井裂缝簇数优化方法，并进行了实例应用分析.

1 数值模型建立

1.1 物理模型建立

假设页岩油藏内有一口体积压裂水平井(如图1所示)，地层以及流体满足以下假设条件：

(1)上下封闭、水平无限大(或封闭)油藏，厚度为h，分为三个区，内区为体积压裂改造区，采用Warren-Root[18]双孔单渗模型来表征，由基质系统和裂缝系统组成，基质系统作为流体的储集空间(渗透率为km，孔隙度为φm)，裂缝系统作为流体的渗流通道(渗透率为kxf，孔隙度为φxf).过渡区为受效区，采用单一介质描述，且考虑储层应力敏感特性(用下标2表示).外区为非改造区，渗透率低，产量贡献可忽略.

(2)原始条件下油藏压力处处相等，即原始地层压力为pi.

(3)水平井平行于x轴，水平井长度为Lh，水力压裂主裂缝条数为nf，裂缝半长为Xf，裂缝渗透率为kf，裂缝段间距为2a，则改造区长度为2nfa，改造区宽度设为We(We≥Xf) ，外边界为有限边界时，外边界长度Lb，外边界宽度We.

(4)流体渗流服从达西定律，具有恒定的压缩系数和粘度，单相可压缩.

(5)忽略毛管力和重力的影响，流体在地层中作达西渗流，且渗流过程等温.

(6)井以某一恒定产量进行生产，井筒中流动为无限导流.

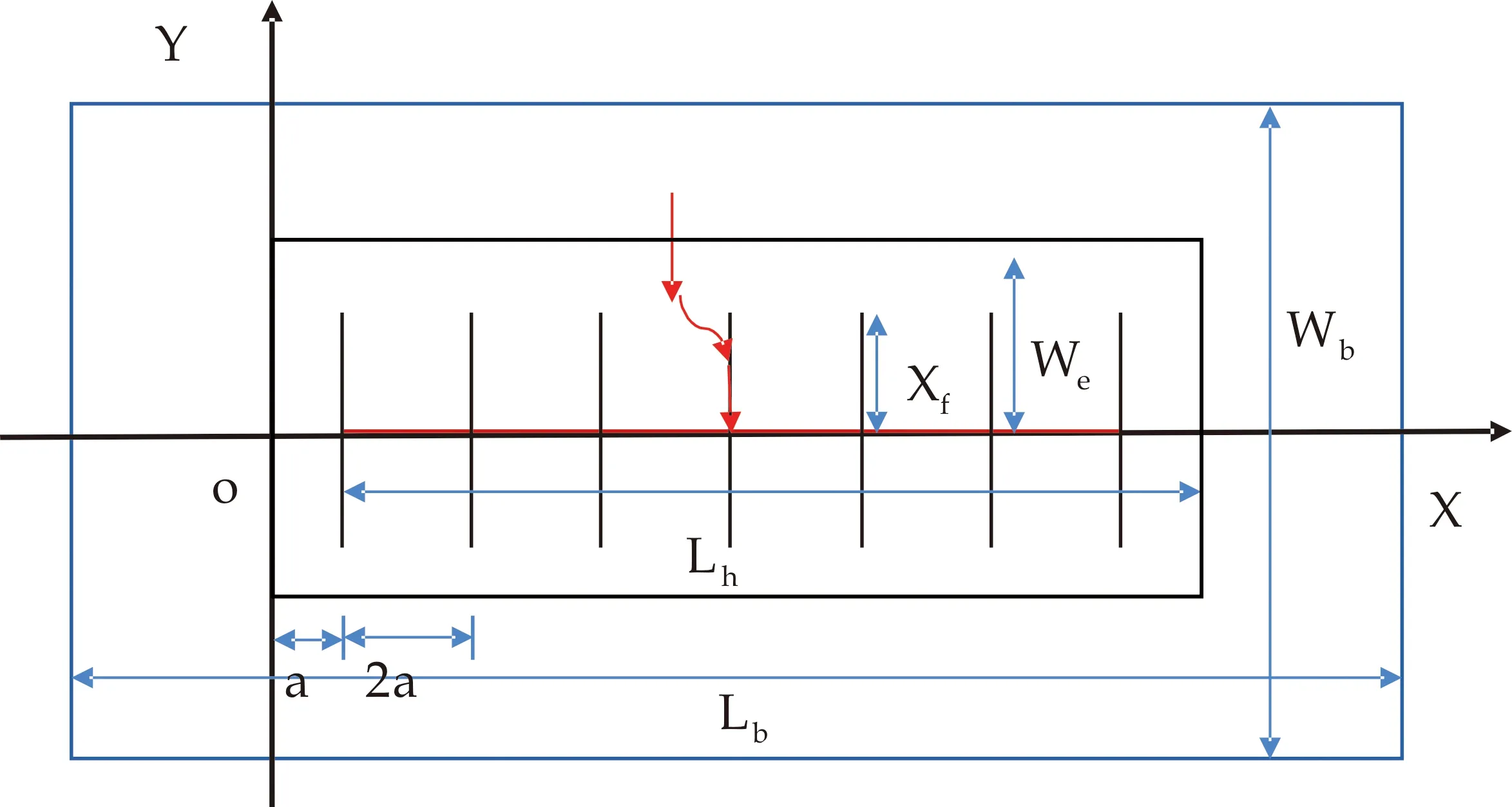
图1 矩形改造区体积压裂水平井渗流物理模型

1.2 数学模型建立

如图1所示，对于第l条裂缝，假设其裂缝内压力为plf，裂缝流量为ql，裂缝与井筒交点坐标为(xl,yl,zl).由于Xf/h较大，因此认为流体在狭窄条带状的裂缝中做拟线性流[19].

1.2.1 主裂缝方程

(1)

忽略裂缝中流体的压缩性，针对第L条裂缝建立有限导流裂缝的流动方程为，

(2)

初始条件：

plf(x,y,t=0)=pi

(3)

井底流量条件：

(4)

裂缝与壁面流量相等条件：

(5)

物质平衡条件，

(6)

1.2.2 改造区方程(考虑双重介质)

(7)

(8)

初始条件：

psf(x,y,t=0)=pi

(9)

改造区与非改造区边界处压力和产量耦合条件：

psf=p2

(10)

(11)

1.2.3 非改造区方程(考虑储层应力敏感)

(12)

初始条件：

p2(x,y,t=0)=pi

(13)

外边界条件：

p2(x,y,t)|x→∞=pi

(14)

封闭边界：

(15)

为了方便模型的求解，本文引入一系列无因次参数.

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

在上述公式中：pi为原始地层压力，MPa；p*D为无因次井底压力；r为改造区半径，m；rw为井筒半径，m；rD为无因次径向半径；ω为缝网体积比，无因次；λ为窜流系数，无因次；C为井筒储集系数，m3/MPa；CD为无因次井筒储集系数；γD为无因次渗透率模数；xD为无因次x方向距离；yD为无因次y方向距离；μ为流体黏度，mPa·s；φ为孔隙度，小数；Ct为综合压缩系数，MPa-1；K为渗透率，D；h为储层有效厚度，m；q为生产流量，m3/d；qf为水力裂缝流量，m3/d；μ为流体粘度，mPa·s；B为体积系数，m3/m3；wF为裂缝宽度，m；xF为主裂缝半长，即改造区边界大小，m；t为生产时间，h；tD为无因次时间；M1,2为改造区与非改造区流度比，无量纲；M1为改造区流度，μm2/(mPa·s)；M2为非改造区流度，μm2/(mPa·s)；W为改造区与非改造区储能系数比，无量纲；u为Laplace空间变量；kf为水力裂缝有效渗透率，μm2；km为储层基质渗透率，μm2；ksf为储层微裂缝渗透率，μm2；k2为储层非改造区渗透率，μm2；φm为储层基质孔隙度，小数；φsf为储层微裂缝孔隙度，小数；φ2为非改造区孔隙度，小数；

1.3 数学模型求解

1.3.1 模型拉普拉斯变换

(1)主裂缝模型拉普拉斯变换

(27)

(2)改造区模型拉普拉斯变换

(28)

(3)非改造区模型拉普拉斯变换

由于非改造区考虑了储层的应力敏感性，渗流方程存在很强的非线性，直接求解十分困难，为此对于非改造区引入摄动变换式进行线性化处理，得到其解析解.

非改造区无因次井底压力：

(29)

非改造区模型无因次化：

(30)

将式(29)代入式(30)可得：

(31)

1.3.2 方程差分离散求解

上述方程为二阶偏微分方程，为求解上述方程，需将上述方程差分离散.在Laplace空间中，主裂缝为一维渗流，变量只有一个，微裂缝和外部油藏为平面渗流，变量为两个，但考虑到Laplace空间中u(k)(k=1,2…10)的存在，为了使Laplace反演更方便，将微裂缝和外部油藏的变量记为(i，j，k)，主裂缝记为(j，k).

(1)主裂缝

(32)

(2)改造区

(33)

(3)非改造区

(34)

利用matlab进行编程计算，采用Stehfest数值反演将求得的拉氏空间解反演为实空间解，计算公式为：

(35)

(36)

式(35)中：N一般取4～18之间的偶数.

(37)

1.4 数值模型特征分析

1.4.1 模型特征曲线分析

建立矩形改造区体积压裂模型理论压差和压力差导数特征曲线(如表1和图2所示).

表1 矩形改造区体积压裂水平井数值模型参数表

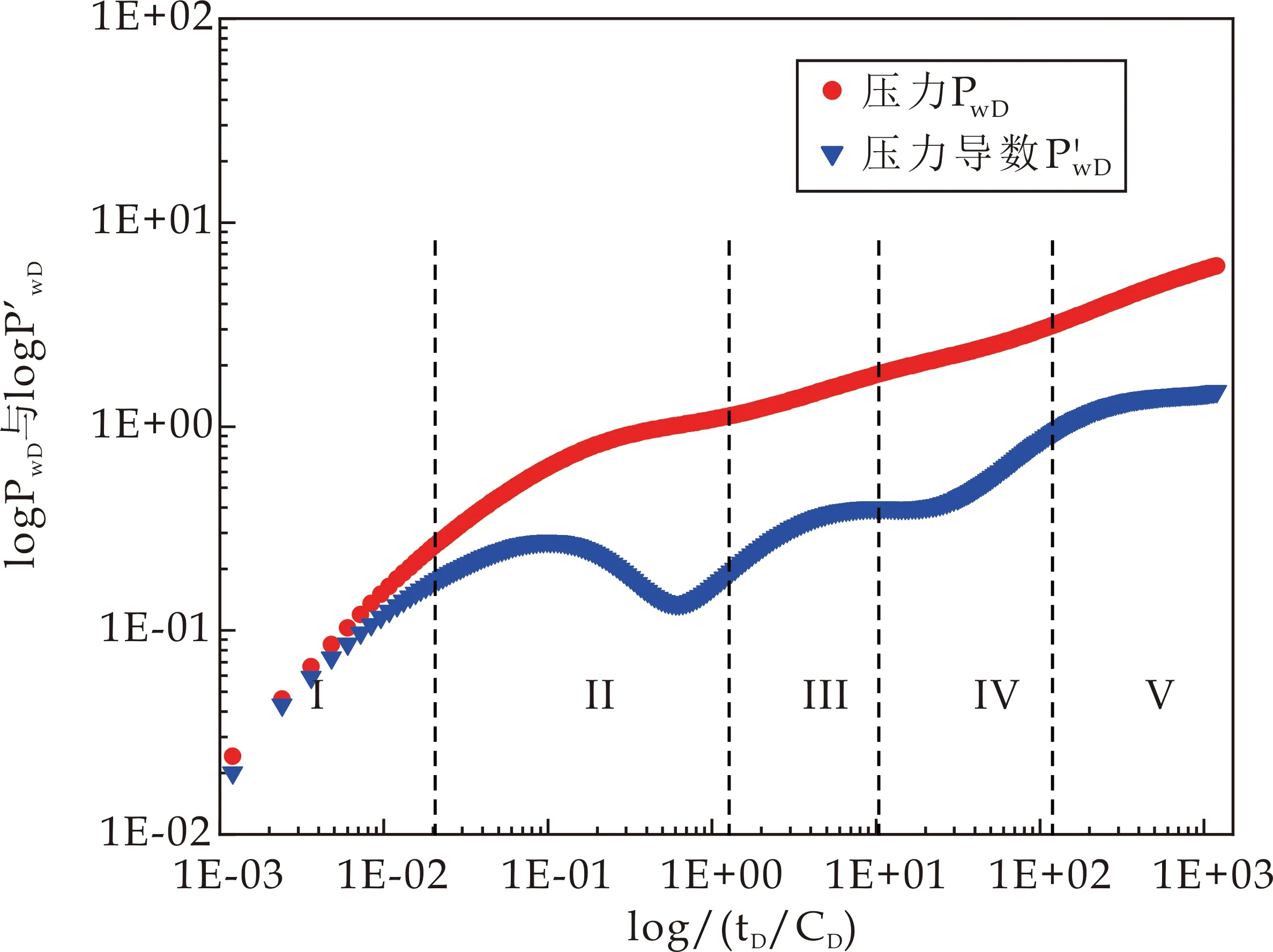
图2 矩形改造区体积压裂模型理论特征曲线

根据压力和压力导数曲线特征， 模型曲线特征进行流动段划分，从图2可看出，矩形改造区体积压裂模型的理论压力和压力导数特征曲线可分为5个阶段.

(1)井筒储集和表皮阶段：受井筒储集效应和表皮效应影响，压力与压力导数曲线重合且斜率为1，后出现“驼峰”形状，“驼峰”形状的高低受井储系数和表皮系数的综合影响.

(2)窜流阶段：基质向裂缝的窜流阶段，压力导数曲线出现下凹.

(3)改造区系统径向流阶段：压力导数曲线表现为水平段.

(4)过渡阶段：改造区向非改造区的流动，压力和压力导数曲线上翘.

(5)油藏系统径向流动阶段：压力导数曲线表现为水平.

1.4.2 模型敏感性分析

由于本篇文章主要研究裂缝簇数的优化问题，所以在此仅分析裂缝条数对特征曲线的影响.

在其他参数一定的情况下，分别计算裂缝条数为3，6和12 时压力和压力导数曲线.由图3 可以看出裂缝条数主要影响压力和压力导数的前期和中期，随着裂缝条数的增加，两条曲线整体下移，其中最大的影响是第三阶段，改造区系统径向流逐渐不明显(水平段逐渐消失).原因在水平井筒和裂缝半长不变的情况下，随着裂缝条数的增加，裂缝间的干扰变明显且提前，裂缝间压力波的互相干扰导致第三阶段的水平线逐渐消失.

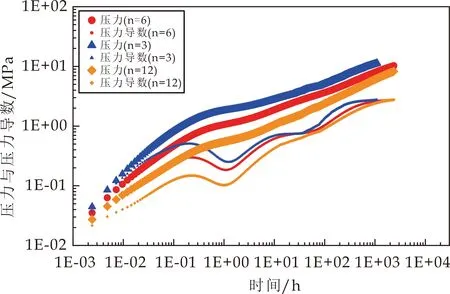
图3 裂缝条数对试井曲线的影响

1.5 数值模型的可靠性分析

为说明建立数值模型的可靠性和实用性，利用数值模型对JHW023井的试井测试数据和生产动态数据进行拟合应用.JHW023井自2017年8月6日闷井测试结束后开始生产，至2018年9月6日进行压力恢复测试，期间总共生产了398天，累计产油量16 241.9 m3.首先建立数值模型，如图4所示，对2018年压力恢复测试资料进行拟合解释(如图5所示)，获得相关参数.进一步应用数值模型进行生产动态历史拟合(如图6所示)，其参数如表2所示，获得理论累产油量为16 035.1 m3.与实际产油量相对误差为1.27%，拟合效果如图5和6所示.由图可知，拟合效果较好，参数合理且符合实际，说明建立的数值模拟具有较好的可靠性和实用性.

图4 JHW023数值模型图

表2 JHW023数值模型参数表

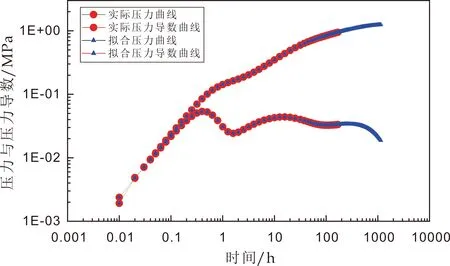
图5 JHW023压力恢复拟合结果图

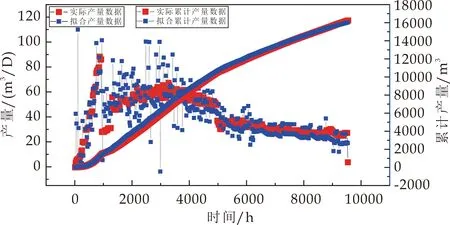
(a)JHW023产量拟合结果图

2 实例应用分析

基于新疆页岩油藏2017～2018年压裂水平井的试井分析结果的平均参数(如表3所示)，建立单井解析模型.设计不同裂缝条数方案，计算累计产量，观察两年累计产油量和裂缝数的变化趋势.

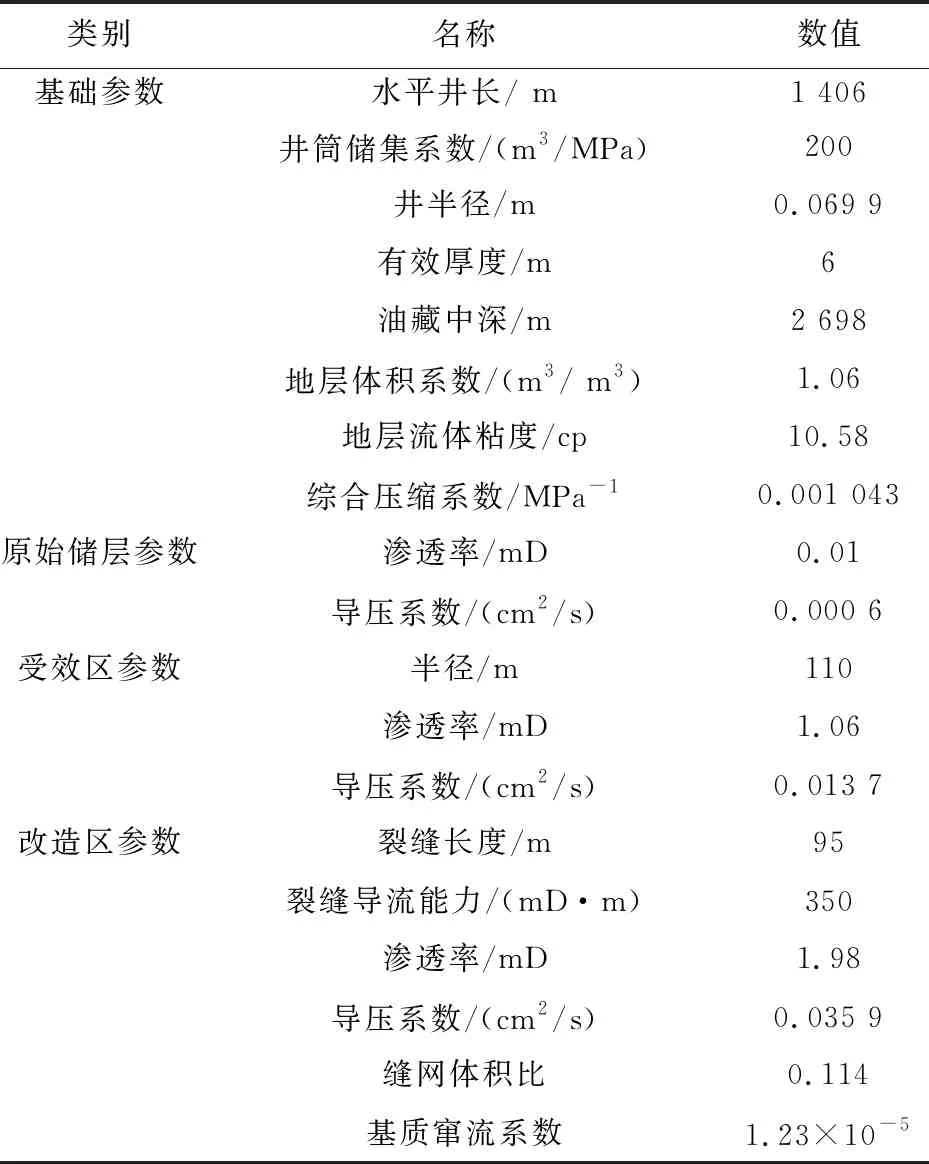
表3 新疆昌吉页岩油田平均参数表

以相同参数建立单井数值模型，观察裂缝簇间压力波传播范围，观察变化趋势，如图7所示，可看出在簇间距介于20～70 m范围时，即裂缝簇数为20～70时，随着簇间距的减小，压力波的传播范围逐渐增大.

图7 不同簇间距压力波传播范围

利用建立的解析模型，设计不同裂缝条数方案，如表4所示.计算两年累计产量，观察两年累计产油量和簇间距的变化趋势，如图8所示.

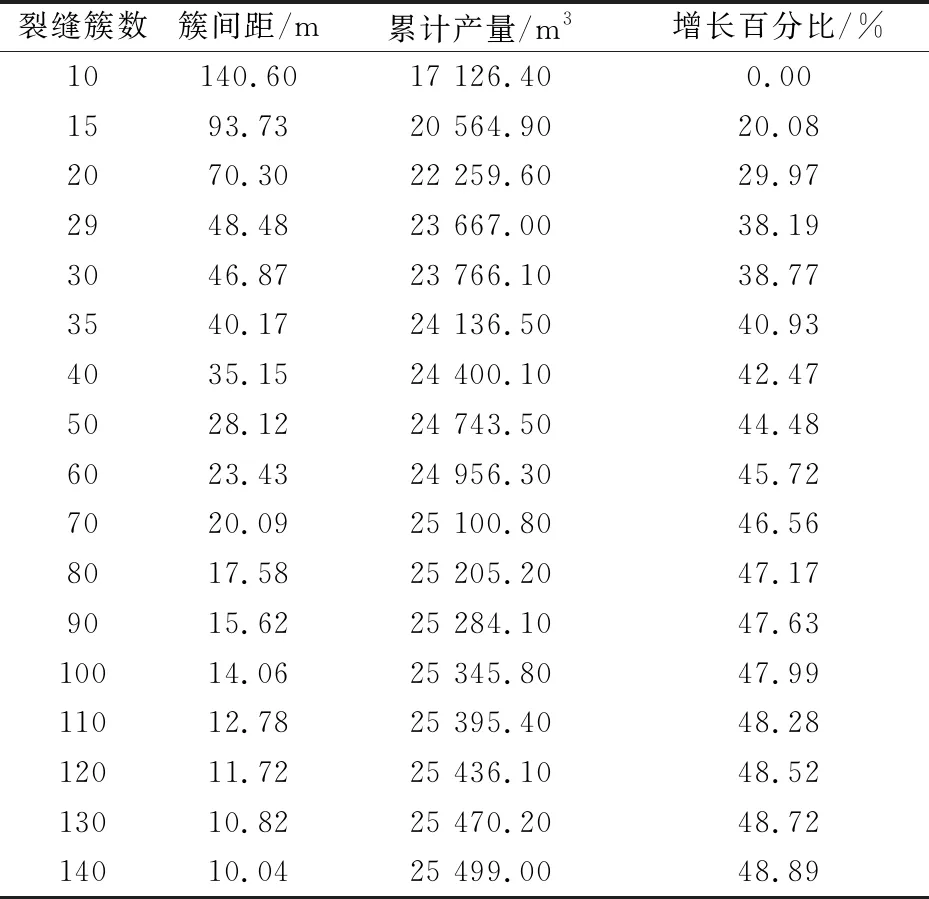
表4 不同裂缝条数方案表

图8 两年累计产油量变化曲线

通过表4和图8可以分析得到，当簇间距小于18 m后，即裂缝簇数大于80条，两年累计产油量的增长趋势趋于平缓，可以确定目前压裂规模多段压裂水平井合理的簇间距范围在15～20 m左右，裂缝簇数为70～80.由最优裂缝簇数为75的理论模型进行产量预测，计算发现昌吉油田页岩油藏压裂水平井的两年累计产油量为25 150 m3.

3 结论及建议

(1)利用不稳定渗流理论建立了多段压裂水平井多井数值模型，在典型多段压裂水平井的储量动用充分的原则，提出了一套裂缝簇数优化方法，并针对昌吉油田页岩油藏多段压裂水平井进行了实例应用分析.

(2)矩形改造区体积压裂模型的理论压力和压力导数特征曲线主要由5个阶段组成：井筒储集和表皮阶段、窜流阶段、改造区系统径向流动阶段、过渡阶段、油藏系统径向流动阶段，其中随着裂缝条数的增加，两条曲线整体下移，其中最大的影响是第三阶段，改造区系统径向流逐渐不明显(水平段逐渐消失).

(3)利用数值模型对典型井的压力恢复测试资料进行拟合解释，进一步应用数值模型进行生产动态历史拟合，获得理论累产油量与实际产油量相对误差为1.27%.拟合效果较好，参数合理且符合实际，说明建立的数值模拟具有较好的可靠性和实用性.

(4)结果发现，当簇间距小于18 m后，即裂缝簇数大于80条，累计产油量的增长趋势趋于平缓，可以确定目前压裂规模多段压裂水平井合理簇间距范围在15～20 m左右，裂缝簇数为70～80.由最优裂缝簇数为75的理论模型进行产量预测，结果表明昌吉油田页岩油藏多段压裂水平井的两年累计产油量为25 150 m3.