一元函数微分和多元函数全微分的教学新探

王珺 徐富强 郝江锋

摘要：微分概念是微积分的核心概念，它直接影响到后续积分概念的学习。一元函数微分和多元函数全微分一直是教学的难点，其原因在于教材对于微分介绍较少，且微分的定义从字面表达上与“无限细分，以直代曲”的重要思想脱节。着重从几何角度出发，在课堂教学中带领学生分析“微分”和“全微分”的定义中“无限细分，以直代曲”的深刻含义，并在此基础上避开晦涩难懂的理论证明和推导，通过几何直观，用通俗易懂的语言解释全微分与连续、偏导数、方向导数以及偏导数连续之间的关系。

关键词：微分;全微分;几何;以直代曲

中图分类号： G642.1   文献标识码： A

1 引言

微积分是高等数学的重要组成部分，20世纪杰出的数学家约翰·冯·诺伊曼在论述微积分时写道：“微积分是现代数学取得的最高的成就，对它的重要性怎样估计也是不会过分的[1]。”微积分俨如一座桥梁，使学生们通过它从基础性的初等数学走向富于挑战性的高等数学，并且面对令人眼花缭乱的转换，从有限量转向无限量，从离散性转向连续性，从肤浅的表象转向深刻的本质[1]。而在微积分中，微分又是核心概念。对于微分概念正确理解与否，会直接影响后续學生对积分概念的理解以及微元法的应用，而在一元函数微分和多元函数全微分的教学过程中，大部分学生反映概念太过抽象，对“微分”和“全微分”定义的理解只能停留在表面，不能深刻理解定义的深层含义，而且在国内大部分教材上[2-4]，介绍“微分”的篇幅远远少于“导数”，甚至有学生认为：前面有了导数的概念，微分这个概念是多余的。导致学生有这些想法的主要原因在于无论是“微分”还是“全微分”的定义，从字面意思看，与朴素的微分思想“无限细分，以直代曲”脱节，并且许多教材[2-4]在引入微分定义之前，都会将一块正方形金属薄片热胀冷缩的问题作为引例，而在这个引例中也没有体现出“无限细分，以直代曲”的思想，这让学生在学习时更是一头雾水。本文从几何角度出发，避免抽象的理论推导，层层深入，带领学生重点分析在“微分”和“全微分”的定义中蕴含着“无限细分，以直代曲”的重要思想，进而从几何角度形象直观地解释多元函数全微分与连续、偏导数、方向导数和偏导数连续之间的关系。

2 一元函数微分教学新探

定义1[2] 设函数y=f（x）在某区间内有定义，x0及x0+Δx在这区间内，如果增量

Δy=f（x0+Δx）-f（x0）

可表示为

Δy=AΔx+O（Δx），（1）

其中A是不依赖于Δx的常数，那么称函数y=f（x）在点x0是可微的，而AΔx叫做函数y=f（x）在点x0相应于自变量增量Δx的微分，记作dy，即

dy=AΔx

下面将从几何角度解释定义1，从中挖掘“无限细分，以直代曲”的深刻含义。

定义1中包含了两个概念：一元函数在一点可微的概念和在一点微分的概念。首先，从几何角度解释函数f（x）在一点可微。从定义1中可知，只要（1）式成立，函数f（x）在点x0处便可微，但（1）式太过抽象，现将（1）式做如下等价变形：

f（x0+Δx）=f（x0）+AΔx+O（Δx），（2）

令x=x+Δx，则（2）式等价于

f（x）=f（x0）+A（x-x0）+O（Δx），（3）

（3）式左边表示点（x0，f（x0））附近的曲线，将（3）式右端前两项和记为

y=f（x0）+A（x-x0），（4）

式为一个关于x的一次函数，且点（x0，f（x0））满足（4）式，即（4）式表示一条通过点（x0，f（x0））的非竖直直线（即：不平行于y轴的直线），其中常数A为该直线的斜率。

因此，一元函数f（x）在一点可微的定义可以重新描述为：如果存在一条过点（x0，f（x0））的非竖直直线近似替代点（x0，f（x0））附近的曲线f（x），使得误差达到O（Δx），则函数y=f（x）在点x0处可微。

但是这种几何解释仍然不够直观，究竟怎样的直线才能使得近似替代的误差达到O（Δx）呢？从上文中我们不得而知！从而引入一元函数可微的充要条件。

定理1[2] 函数f（x）在点x0可微的充要条件是函数f（x）在点x0可导，且A=f '（x0）。

定理1告诉我们，如果满足误差能够达到O（Δx）的直线确实存在，则该直线的斜率A=f '（x0），即该直线必为点（x0，f（x0））处的切线。

于是一元函数f（x）在一点处可微的几何意义为：如果曲线y=f（x）在点（x0，f（x0））处有一条不平行于y轴的切线，则函数y=f（x）在点（x0，f（x0））处可微，或者可以更形象地解释为：将曲线f（x）在点（x0，f（x0））附近放大，当放大到某一程度，曲线看上去像一条非竖直的直线，则函数f（x）在点x0可微。这比单纯从（1）式去理解函数可微的含义要直观形象很多。

反之，如曲线f（x）在点（x0，f（x0））处没有非竖直的切线，则函数f（x）在点（x0，f（x0））处不可微，即只有三种情况不可微：（1）曲线不连续，则不可微（如图1（a））;（2）曲线连续但出现尖点，则不可微，例如：y=|x|在点x=0处为尖点，曲线在尖点处没有切线，所以不可微（如图1（b））;（3）曲线连续但出现竖直切线，则不可微，例如：在点x=0处有竖直切线（红色实线），所以不可微（如图1（c））。

（a）曲线在x0处不连续         （b） 曲线在x=0处为尖点不可微    （c）曲线在x=0处有竖直切线

接着，再从几何角度分析函数f（x）在一点微分的概念，由定理1可知，f（x）在点x0处的微分为：dy=f '（x0）Δx，习惯上Δx=dx，则dy=f '（x0）dx。

从图2[2]中可以看出，dy=f '（x0）dx正是圖2中的线段PM，其中蓝色直线为曲线f（x）在点x0处的切线。因此，对于微分dy我们可以这样理解：当对自变量x进行细分，得到x的微分dx，则因变量y也相应地进行了细分，即图2中的线段PN，此时将点（x0，f（x0））处的切线近似替代点（x0，f（x0））附近的曲线，即用线段PM代替线段PN，便得到因变量的微分dy=f '（x0）dx。

综上所述，定义1蕴含着“无限细分，以直代曲”的深刻思想，这也是后续学习积分概念的基础，积分正是微分的相反过程，即“无限求和”，而积分符号“∫”是一个拉长的字母“S”，也表示着“求和（summa）”的意思。在求不规则图形的面积和体积，以及曲线的弧长等问题中，所利用的“微元法”正是“无限细分，无限求和”思想的重要体现，即：先无限细分，再在局部上“以不变代变”或“以直代曲”，求得所求量的近似值，然后在无限变化的过程中实现从“近似”到“精确”的转变，从而得到所求量[5]。另外“微分”概念虽然与“导数”概念互为充要条件，相互等价，但并不是多余的概念，两者反映的问题是完全不一样的，“导数”表示函数在一点处自变量变化所引起的函数因变量变化的快慢程度，而“微分”表示函数在一点处自变量的微小变化所引起的函数因变量改变的近似值[4]。

3 多元函数全微分教学新探

定义2[6] 设函数z=f（x，y）在点（x0，y0）的某邻域内有定义，如果函数在点（x0，y0）的全增量

Δz=f（x0+Δx，y0+Δy）-f（x0，y0）

可表示为

Δz=AΔx+BΔy+O（ρ）                           （5）

其中A、B不依赖于Δx，Δy而仅与x0、y0有关，则称函数z=f（x，y）在点（x0，y0）可微分，而AΔx+BΔy称为函数z=f（x，y）在点（x0，y0）的全微分，记作dz，即

dz=AΔx+BΔy.

不难发现，定义2是定义1的推广，因此定义2的几何意义可以从定义1的几何意义推广而来。将（5）式等价变形为：

f（x0+Δx，y0+Δy）=f（x0，y0）+AΔx+BΔy+O（ρ）              （6）

令x=x0+Δx，y=y0+Δy，则（6）式等价于

f（x，y）=f（x0，y0）+A（x-x0）+B（y-y0）+O（ρ）               （7）

其中为xoy平面上点（x0，y0）与点（x0+Δx，y0+Δy）之间的距离，（7）式左端表示点（x0，y0，f（x0，y0））附近的曲面，将（7）式右端前三项的和记为

z=f（x0，y0）+A（x-x0）+B（y-y0），（8）

式为一个三元一次方程，且点（x0，y0，f（x0，y0））满足（8）式，由空间解析几何的知识可知：（8）式表示一张通过点（x0，y0，f（x0，y0））的平面，且该平面法向量为n=（A，B，-1），又因为法向量n不可能与z轴垂直，所以该平面不与z轴平行，是一张非竖直的平面。

因此，二元函数f（x，y）在一点可微的定义可以重新描述为：如果存在一张过点P（x0，y0，f（x0，y0））的非竖直平面近似替代点P（x0，y0，f（x0，y0））附近的曲面f（x，y），使得误差达到O（ρ），则函数f（x，y）在点（x0，y0）处可微。

上述二元函数f（x，y）可微的几何解释仍然不直观，继续给出函数f（x，y）在一点可微的必要条件。

定理2[6]（可微的必要条件） 如果函数z=f（x，y）在点（x0，y0）可微分，则该函数在（x0，y0）的偏导数必定存在，且函数。

定理2告诉我们，如果使得误差达到O（ρ）的平面确实存在，则该平面的法向量为n=（fx（x0，y0），fy（x0，y0），-1），即该平面必为点（x0，y0，f（x0，y0））处的切平面：

z=f（x0，y0）+fx（x0，y0）（x-x0）+fy（x0，y0）（y-y0），

于是二元函数f（x，y）在一点处可微的几何意义为：如果曲面z=f（x，y）在点（x0，y0，f（x0，y0））处有一张不平行于z轴的切平面，则函数z=f（x，y）在点（x0，y0，f（x0，y0））处可微，或者可以更形象地解释为：将曲面f（x，y）在点（x0，y0，f（x0，y0））附近放大，当放大到某一程度，曲面看上去像一条非竖直的平面，则函数f（x，y）在点（x0，y0）可微。反之，如曲面f（x，y）在点（x0，y0，f（x0，y0））处没有非竖直的切平面，则函数f（x，y）在点（x0，y0，f（x0，y0））处不可微。

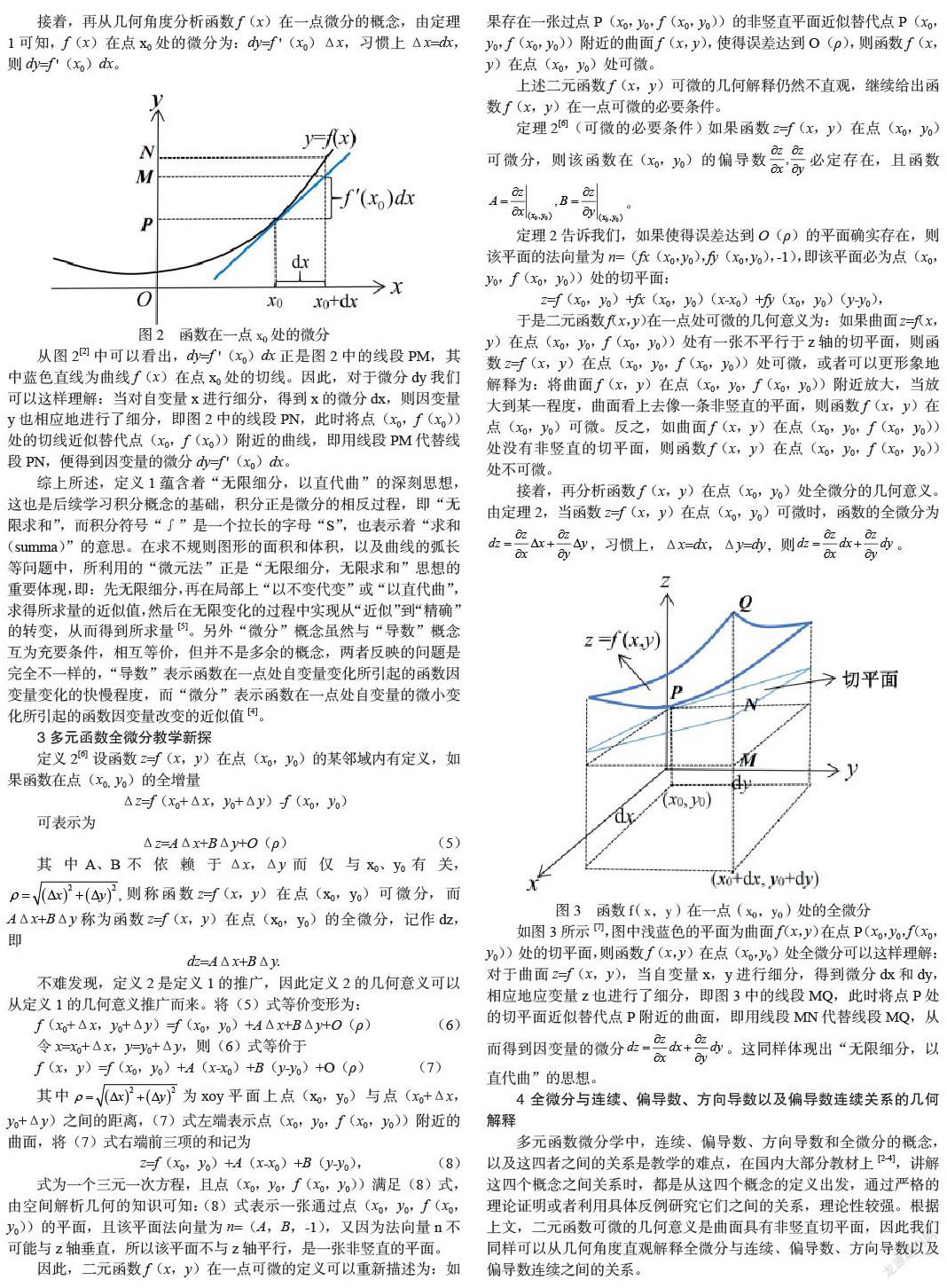
接着，再分析函数f（x，y）在点（x0，y0）处全微分的几何意义。由定理2，当函数z=f（x，y）在点（x0，y0）可微时，函数的全微分为，习惯上，Δx=dx，Δy=dy，则。

如图3所示[7]，图中浅蓝色的平面为曲面f（x，y）在点P（x0，y0，f（x0，y0））处的切平面，则函数f（x，y）在点（x0，y0）处全微分可以这样理解：对于曲面z=f（x，y），当自变量x，y进行细分，得到微分dx和dy，相应地应变量z也进行了细分，即图3中的线段MQ，此时将点P处的切平面近似替代点P附近的曲面，即用线段MN代替线段MQ，从而得到因变量的微分。这同样体现出“无限细分，以直代曲”的思想。

4 全微分与连续、偏导数、方向导数以及偏导数连续关系的几何解释

多元函数微分学中，连续、偏导数、方向导数和全微分的概念，以及这四者之间的关系是教学的难点，在国内大部分教材上[2-4]，讲解这四个概念之间关系时，都是从这四个概念的定义出发，通过严格的理论证明或者利用具体反例研究它们之间的关系，理论性较强。根据上文，二元函数可微的几何意义是曲面具有非竖直切平面，因此我们同样可以从几何角度直观解释全微分与连续、偏导数、方向导数以及偏导数连续之间的关系。

4.1 全微分与连续关系的几何解释

二元函数连续的几何意义[8]：连续函数的图形是一个无孔隙、无裂缝而绵密的曲面。从几何直观上，一张曲面如果在一点有非竖直切平面，则曲面在该点肯定无孔隙、无裂缝;反之，如果曲面出现尖点，在尖点处虽然无孔隙、无裂缝，但曲面在尖点处没有切平面，例如，可以在课堂上给学生展示这样一个小实验：将一张A4打印纸揉成一个纸团，再展开，A4纸出现了许多折痕，在折痕处纸是没有孔隙，没有裂缝的，但是在折痕处它没有切平面。因此，对于多元函数，可微必连续，但连续不一定可微。

4.2 全微分与偏导数、方向导数关系的几何解释

二元函数z=f（x，y）的偏导数和方向导数是曲面z=f（x，y）沿不同方向变化率的精确刻画，其中偏导数是曲面z=f（x，y）沿坐标轴正方向的变化率，方向导数是曲面z=f（x，y）沿任一方向的变化率。

如果曲面z=f（x，y）在一点处具有非竖直切平面，则在曲面z=f（x，y）上过该点的任意曲线都会在该点都有切线，而这些切线的斜率正是曲面沿该切线方向的变化率，因此从这可以看出，如果函数z=f（x，y）在一点处可微，则函数z=f（x，y）在这点处的偏导数和方向导数都存在。反之，如图4所示，曲面在尖点M处沿各个方向的方向导数都存在，但在曲线上过点M作曲线，曲线在点M 处不具有切线，所以曲面在点M处没有切平面，因此函数在一点处仅仅偏导数或者方向导数存在，则不能推出函数在该点处可微。

4.3 全微分与偏导数连续关系的几何解释

定理3[6] （可微的充分条件）如果函数z=f（x，y）的偏导数在点（x，y）连续，则函数在该点可微分。

从几何直观上，曲面光滑，则曲面一定有切平面。曲面光滑指曲面上各点处都具有切平面，且当点在曲面上连续移动时，切平面也连续转动[2]，而法向量和切平面垂直，切平面连续转动的同时，法向量也在连续转动。当曲面方程为二元函数z=f（x，y）时，其法向量为：n=（fx，fy，-1），因此正如定理3所说，当偏导数fx，fy连续时，法向量在连续转动，则曲面光滑，曲面必有切平面，且此法向量n=（fx，fy，-1）不与z轴垂直，即切平面不与z轴平行，所以对应函数z=f（x，y）可微。反之，曲面有切平面，但曲面不一定光滑，即函数z=f（x，y）可微，不能推出偏导数fx，fy连续，如下面例1。

例1[8] 函数

的图形为：

通过[8]可知，函数f（x，y）在点（0，0）处可微，而偏导数fx，fy在点（0，0）不连续，即曲面在点（0，0）处有切平面z=0，但由于曲面在点（0，0）附近无限震荡，越接近点（0，0）震荡的频率越高，所以曲面在原点（0，0）处不光滑。

5 结束语

在“微分”和“全微分”的教学过程中，大部分学生会熟练掌握“微分”和“全微分”的计算方法，但对“微分”和“全微分”蕴含的本质思想却不是很了解。本文在微分和全微分的教学过程中，避免了抽象、晦涩难懂的理论证明和推导，从几何角度形象地解释了“微分”和“全微分”的定义，充分体现出微分的重要思想“无限细分、以直代曲”。同時，我们也形象生动地给出了全微分与连续、偏导数、方向导数以及偏导数连续的关系。采用新的教学方法完成“微分”和“全微分”的教学，学生普遍反映较好，并且这也为后续讲解“积分”的概念做好充分的准备。

参考文献：

[1]William Dunham（著），李伯民，汪军，张怀勇（译）. 微积分的历程—从牛顿到勒贝格[M]. 北京：人民邮电出版社，2017：1.

[2]同济大学数学系. 高等数学上册（第6版）[M]. 北京：高等教育出版社，2012：113-116.

[3]华东师范大学数学系. 数学分析上册（第3版）[M]. 北京：高等教育出版社，2002：111-112.

[4]巢湖学院应用数学学院. 应用高等数学上册[M]. 合肥：中国科学技术大学出版社，2016：72-74.

[5]朱家生. 数学史[M]. 北京：高等教育出版社，2005：110.

[6]同济大学数学系. 高等数学下册（第6版）[M]. 北京：高等教育出版社，2009：70-73.

[7]华东师范大学数学系. 数学分析下册（第3版）[M]. 北京：高等教育出版社，2002：107-115.

[8]滕文凯. 二元函数微分学分析性质的相互关系及其几何意义[J]. 承德民族师专学报，1994（2）：1-8.

基金项目：安徽省高等学校省级重点教学研究项目“基于超星学习通的混合式教学模式研究与实践——以大学数学公共基础课为例”（2019jyxm0393）;巢湖学院校级一流课程建设项目“高等数学”（chylkc034）;巢湖学院精品在线开放课程“线性代数”（ch18zxkc17）;巢湖学院重点教学研究项目“基于SPOC和翻转课堂的线性代数混合式教学改革与实践”（ch19jxyj11）

作者简介：王珺（1984—），女，安徽安庆人，硕士，讲师，研究方向为计算数学