基于误差分类的风电功率区间评估

韩 丽，乔 妍，景惠甜

（中国矿业大学电气与动力工程学院,江苏省徐州市221116）

0 引言

作为可再生能源的风力发电在世界各地得到了普遍的应用和发展,但由于风电本身的间歇性、随机性和波动性导致很难对其进行准确预测。由于预测误差的普遍存在,对于电力系统规划和运行决策而言,能够得到预测数值波动范围的区间评估至关重要［1］。

预测误差的主要评估方法有参数型方法和非参数型方法［2］。参数型方法假设预测误差数据服从某种特定的分布形式,如高斯分布［3］、贝塔分布［4］、t 分布［5］等。文献［6］提出了一种基于风电场功率特性曲线的预测误差分布估计方法,但对这种基于误差拟合的方法而言,误差拟合效果的优劣程度会对风电功率评估区间的范围造成很大影响,事实上风电的非线性使整体功率预测误差不服从于任何已知分布的函数,而各种分布拟合函数应用于不同时刻,其效果也存在较大差异。非参数型方法不用预先假设预测误差的分布形式,但需要的数据量大、计算复杂,常用的方法有分位数回归［7-8］、核密度估计［9-10］等。文献［11］将误差分为模型误差和数据噪声误差2 类,通过确定2 类误差之间的方差来构建评估区间,考虑了不同类型的误差对于风电区间评估的影响,但该方法给出的评估区间范围比较大,对于风电功率短时波动的识别不明显。文献［12］用模糊C 均值聚类将历史数据划分为多个子区间,再利用核密度估计计算各子区间的概率密度函数,虽然采用聚类算法可以提高划分类别的有效性,但忽视了各个子区间的相关性,未考虑到数据整体的时序相关性。

综上所述,目前区间评估采用的评估模型主要存在两方面问题:一是利用误差概率分别得到的误差区间较大,且得到的是统计意义上的值,无法反映风电实时功率变化时误差的波动；二是分析预测误差过程中未能考虑其时序特性,将数据划分为多个类别或子区间分别进行评估,忽视了误差和功率数据的整体时序性以及误差的分布特性。

为此,本文提出一种基于K-means 聚类和长短期记忆（long short-term memory,LSTM）神经网络的误差区间评估模型。首先,对风电功率预测误差数据进行K-means 聚类,对聚类后每种误差类型赋以特征值；再将其与风电功率数据和预测误差数据一同代入LSTM 模型中；最后,将得到的误差类型所对应的误差值与预测风电功率值叠加后得到风电功率的评估区间。

1 基于K-means 聚类的误差类别分析

风电功率的点预测必然存在预测误差,不同的点预测方法会产生具有不同分布特性的误差,而掌握误差数据的特点是研究区间评估的关键［13］。为准确掌握误差数据的分布特点和时序特性,首先需要通过聚类算法对误差进行分类处理。

1.1 K-means 算法的基本原理

K-means 算法作为最流行的聚类算法,由Macqueen［14］于1967 年 提 出。K-means 算 法 是 一 种迭代求解的聚类分析算法,且是一种无监督学习。其以距离函数作为聚类指标［15］,将大量数据集划分为预定义数量的聚类,从而可以判断聚类样本之间的相似度。相似度与数据对象间的距离成反比,即相似度越大,距离越小。常用的距离函数是欧氏距离,表达式为:

式中:x 和y 为n 维实数域上的任意两点,x=[ x1,x2,…,xn],y=[ y1,y2,…,yn]；D(x,y)为 两 点间的欧氏距离。

K-means 算法需要预先指定初始聚类数目和初始聚类中心,根据数据对象与聚类中心之间的相似度,不断更新聚类中心的位置,不断降低类簇的误差平方和（sum of squared error,SSE）,当SSE 不再变化或目标函数收敛时,聚类结束,得到最终结果［16］。

1.2 基于K-means 聚类的误差类别分析

风电功率预测误差具有“尖峰厚尾”的特点［17-18］,大多数误差数据较为集中地分布在某一小数值附近,而有一些零散的误差数据分布范围较广且数值较大。利用正态分布和t 分布拟合的误差结果见附录A 图A1,这2 种分布函数在“峰”“尾”处存在较大拟合误差。

如果不对误差进行有效分类,将使得评估方法的误差区间范围大且精度不够高。因此,依据误差分布特性,在数据预处理阶段对预测误差进行分类十分必要。人为划分误差分类区间上下限很难保证符合误差分布特性,而K-means 算法基于欧氏距离这一指标对风电预测误差进行分类,使误差特性相同的点归为一类,得到类似于概率密度分布图的结果,能刻画出原始预测误差数据的分布特征和类别属性。基于K-means 算法的误差数据处理实现过程如下。

步骤1:随机选择K 个预测误差样本作为初始聚类中心。

步骤2:通过欧氏距离测量聚类中心与其余误差对象之间的距离,并将每个误差对象应用于最近的聚类中心。

步骤3:找到新的聚类中心并以其为中心,计算每个聚类的均值向量,表达式为:

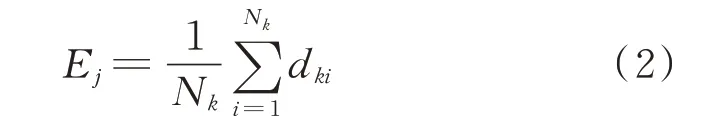
式 中:Ej为 第j 个 簇 的 中 心；dki为 聚 类 类 别k 中 的第i 个数据；Nk为各个簇中样本的数量。

步骤4:在步骤2 和步骤3 之间重复迭代,直到聚类中心不再更改或达到最大迭代次数为止。

利用K-means 对风电功率预测误差进行聚类,数据来源于Elia 公司某比利时风电场［19］,每隔15 min 即1 个数据点。K=5 时的聚类过程和结果如图1（a）至（d）所示。图1（a）为误差按原有时间序列顺序所作的误差波动趋势图。为了更为直观地研究K-means 聚类过程,图1（b）将误差数据画作散点图,并根据大小顺序设置5 个初始聚类中心（如图中红点所示）,分别为-50,-25,0,25,50 MW。依据欧氏距离这一指标不断更新聚类中心,得到新的聚类中心和5 类误差数据（分别用不同颜色进行区分）如图1（c）所示,与附录A 图A1 相结合可以看出误差分布呈现“尖峰厚尾”的特性。图1（d）为数据通过K-means 算法得到的误差分类结果,误差类别分别为Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ类。K =3 时,聚类结果如图1（e）和（f）所示,得到的误差类别分别为Ⅰ,Ⅱ,Ⅲ类。

图1 K-means 算法误差聚类图Fig.1 Error clustering diagram of K-means algorithm

理论上,聚类个数K 越多,误差的分布特性就会表现得越细致,评估区间也会更窄,但聚类个数过多也会带来一些问题:产生误差数值大的类别却出现概率较小的情况。当K=5 时,图1（d）中存在过度分类的现象,误差数值大的第Ⅴ类,出现概率仅为0.06。而风电功率预测误差的类别是确定电网调度所需备用容量的重要参考,从经济性角度,电网运行调度时不可能为小概率出现的场景配置较大的备用裕量。根据图1（e）和（f）,K=3 时的聚类结果不仅能较好地描述误差的分布特性,也不会因为类别过多而产生含有样本数目过少的类别,所以K=3 更适合电力系统调度的实际要求。综上,选择K=3用于风电的区间评估仿真。

2 基于误差分类的区间评估

一般的神经网络模型不能很好地学习具有强随机波动性特征的风电功率和预测误差数据,使得到的区间评估范围不够精确。为了有效学习历史功率和误差序列数据中的规律信息,同时兼顾功率和误差数据的时序性和非线性关系,采用LSTM 模型对误差类别数据进行深度学习,继而得到区间评估结果。

2.1 LSTM 基本原理

LSTM 人工神经网络是一种处理和预测序列数据的神经网络,可以学习输入数据的长期依赖信息,以防止信息传输的梯度消失和梯度爆炸,从而增强了其捕获时间序列动态变化的能力,因此LSTM在风速、风电功率预测中也有了一些初步的应用研究［20-23］。LSTM 神经网络模型的结构是一个具有重复神经网络模块的链结构,包含了输入层、递归隐层和输出层3 个部分［24］。

LSTM 的基本单元内部结构包含3 个控制门:输入门、遗忘门和输出门。门结构控制状态信息的增减,各个门的激活函数it,ft,ot公式［25］为:

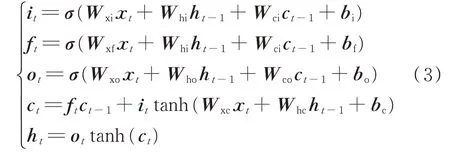
式中:σ（·）为sigmoid（·）函数或tanh（·）函数；xt为当前t 时刻的输入向量；Wxi,Whi,Wci,Wxf,Wxo,Who,Wco,Wxc,Whc为权重参数矩阵；bi,bf,bo,bc为偏置向量；ct为状态单元和即时状态的向量；ht为状态单元当前的输出。

2.2 LSTM 误差类别评估模型设计

由于预测误差的分布情况会根据点预测模型的不同和风电功率的波动而改变,因此本文建立LSTM 评估模型,通过改变模型的输入输出数据类型研究误差与风电功率之间的相关性。对于输入数据而言,若单独考虑功率,就忽略了不同的评估模型对误差类别评估的影响；若单独考虑误差,则忽略了风电功率时间序列的原始波动情况。将点预测模型得到的误差和风电功率这2 种数据组成数据集作为评估模型的输入,使LSTM 网络既能学习到风电的原始波动情况,又能学习到不同的点预测方法带来的不同误差分布情况。而输出数据改变为误差类别,即评估模型可以由功率和误差直接得到误差类别。根据附录A 图A2,可以得出评估模型的表达式为:

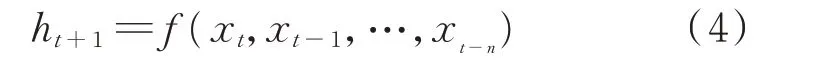
式中:ht+1为预测误差类型；xi为输入数据,由风电功率数据Pi和预测误差数据ei组合而成,即xi=(Pi,ei),i=t,t-1,…,t-n。

传统神经网络模型的学习过程没有学习数据在时序上的联系,而由附录A 图A2 可以看出,LSTM是包含循环的网络,每个神经网络模块会把信息传递给下一个,每一个虚框代表着LSTM 中的记忆元组（cell）,cell 新旧状态的传送类似于传送带,直接在整个链上运行,只有一些少量的线性交互［26］。LSTM 能够在数据分析过程中记住之前发生了什么,做到信息的时序关联问题。由于风电功率的波动会造成预测误差不准确,本文通过LSTM 研究基于时间序列的风电功率与预测误差之间的关联性,实质是利用确定性模型学习误差的分布特性。通过实际风电功率值和实际预测误差值直接评估得到误差类型,继而得到评估误差区间,通过叠加预测功率值得到区间评估结果。评估过程避免了分布拟合的不精确,省去了不确定性模型关于概率密度分布的评估,由功率和误差直接评估误差范围更有利于电力系统工作人员评估风电功率的不确定性和风险因素,做出更为合理的决策。

在建立LSTM 误差类别评估模型的过程中,参数的设置影响着网络预测效果。建模时需要确定的参数主要包括:输入层维数、激活函数、时间步长、隐层数及每层神经元个数、输出变量维数、损失函数。

原则上隐层数和神经元个数越多,网络学习风电数据特性的效果越好,但模型的复杂程度和训练时间都会增加。在实际应用中,要保证每层的神经元数量不因过少而无法学习到规律,不应过多而引发过度拟合,因此要合理地选取预测精度较高且用时较少的方案。经过多次试验,本文提出的最终模型设定如下:输入为2 维向量；LSTM 模块的激活函数采用tanh（·）；时间步长为6,即每次预测要输入6 个历史数据；隐层数为2,第1 层神经元个数定义为64,第2 层神经元个数定义为128；通过全连接层（dense）输出维数为3 的向量,用于表示3 种误差类型；损失函数使用均方误差,并采用高效的Adam 函数作为优化算法。

2.3 区间评估的整体思路

本文为分析风电功率与预测误差类别的相关性,提出了一种基于K-means 聚类和LSTM 网络模型的误差分类区间评估方法。预测方法的整体方案如图2 所示。

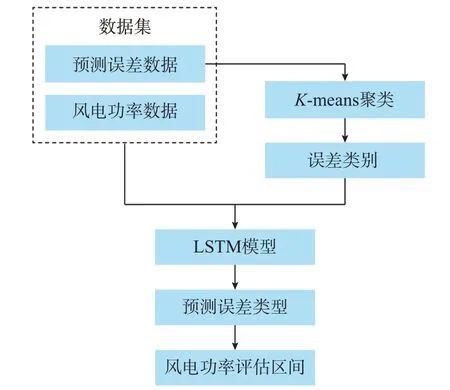
图2 评估模型的整体方案Fig.2 Overall scheme of evaluation model

当前对于风电功率预测的确定性预测模型,输入必须包含历史风电功率数据,采集到的数据有时也会包含风速、温度等数据；输出为预测的风电功率。本文模型虽得到区间评估结果却不属于不确定性预测模型,但相较于一般的确定性预测来说,该方法能够提供风电波动的一个区间范围,能获取更多的信息。首先,通过对误差进行分类,考虑了预测误差的分布情况；然后,通过历史风电功率和预测误差数据直接预测出误差类型及区间,不需要经过其他拟合模型的转换,避免了拟合模型不够准确的拟合效果对评估结果的不利影响；而且LSTM 作为一种专门学习时序信号的网络,更能抓住数据基于时间序列的关联性。因此,该方法得到的评估区间范围更加精确,更利于之后电力系统调度。

3 仿真分析

3.1 区间评估评价指标

本文主要采用以下3 个评价指标［5］,并结合分类混淆矩阵等图表来反映评估结果。1）评估误差类别准确率Acc

式中:N 为评估样本数；当原始误差类别和评估误差类别相同时,ki为1,反之为0；Acc表示评估模型的准确性,其取值范围为［0,1］。Acc越接近于1 表示评估精度越高,Acc越小表示精度越低,区间评估效果越差。

2）评估区间覆盖率IPICP

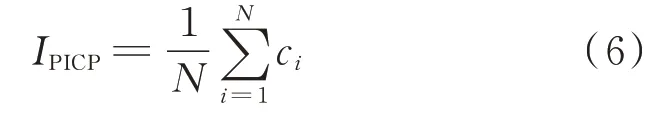
其中,如果评估目标值落入评估区间内,ci=1；反之,ci=0。

风电功率实际落在评估区间内的频率应等于或尽量接近事先给定的置信概率。若某一概率预测的效果较好或可靠性较高,区间覆盖率应较大。

3）区间平均带宽

评估区间的区间宽度δ 为区间上界U 与区间下界L 之差,即

区间平均带宽IPINAW为:

IPINAW能够反映评估区间的清晰度,避免因为单纯追求准确性,使得区间过于保守,无法提供决策价值。

3.2 误差数据的聚类分析

本节采用Elia 网站某比利时风电场2018 年3 月的风电功率数据和短期预测数据得到预测误差数据集,且利用该风电功率数据分别使用持续法（persistence,PER）、AR 时间序列模型、BP 神经网络、Elman 神经网络4 个预测方法进行风电功率预测得到另外4 组不同的预测误差数据集。在基于评估方法的实际应用情况下,本文根据误差“尖峰厚尾”的分布特点,设置聚类个数K=3。以欧氏距离为聚类指标,将误差样本数据通过K-means 聚类分为3 类,对于每组数据设置的初始聚类点均相同,再将得到的误差类别结果转化为误差区间。各误差数据集利用K-means 聚类得到误差区间结果见附录A表A1。

对误差数据进行K-means 聚类,得到Ⅰ,Ⅱ和Ⅲ类误差。由于每种误差数据的波动范围及分布方式均不同,聚类后得到的3 类误差的形式也不尽相同。根据附录A 表A1,5 种误差数据中Elman 的区间波动范围最小,只有64 MW,且整体误差多为负误差。PER 和AR 的误差区间相对更具有对称性,Ⅰ类为正误差,Ⅱ类为关于零对称的正负误差,Ⅲ类为负误差。BP 与Elia 的误差区间更倾向于负误差,其中Elia 数据的误差区间波动范围在5 种误差数据中最大,达到Elman 区间范围的5.5 倍。

3.3 区间评估结果分析

将3.2 节聚类后的误差类别数据按原有的时间序列顺序与风电功率和预测误差数据组合,形成5 个新的数据集,将其代入LSTM 神经网络评估模型中训练,得到的区间评估结果如图3 所示。图3（a）至（e）的区间评估结果的误差来源依次为PER 预测误差、AR 预测误差、BP 预测误差、Elman预测误差和Elia 网站的预测误差。整体算法的预测时间会根据数据来源不同等因素而有些许不同,根据本文数据集求得算法对于一个月数据的平均训练时间为29.36 s,平均测试时间为0.35 s。

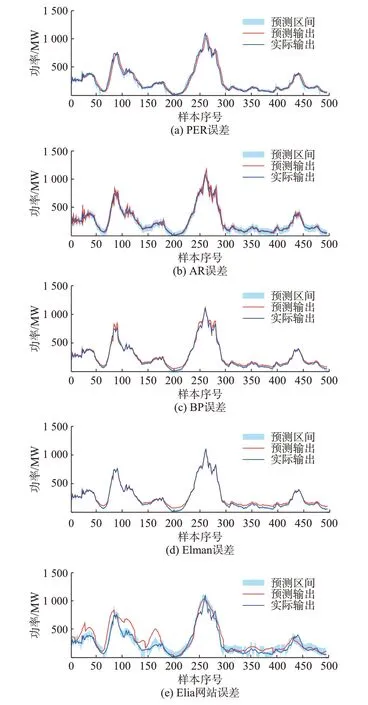
图3 基于不同误差来源的LSTM 区间评估图Fig.3 Interval evaluation diagram of LSTM based on different error sources

根据评估结果计算得到3.1 节的2 个评价指标,评估误差类别准确率Acc表示LSTM 预测误差类别的准确性,评估区间覆盖率IPICP表示实际风电功率在置信区间内的概率。基于Elman 预测误差的评估误差类别准确率Acc和评估区间覆盖率IPICP分别为0.971 9 和0.907 3,分类精度和置信区间评估精度均为最优。基于AR 预测误差和Elia 网站预测误差的区间评估Acc均小于0.9,其IPICP也均不超过0.8,根据附录A 表A1 可知,这2 种误差数据本身的波动范围较大,使其误差变化趋势也更难以预测。也就是说,基于误差分类的区间评估结果不仅与LSTM 模型的评估精度有关,也与原始预测误差的来源即原始风电功率预测方法有关。基于PER 和BP 的Acc相近,分别为0.903 6 和0.931 7,IPICP却相差较大,分别为0.796 4 和0.823 3,是因为每种评估误差类别对应的误差范围都不相同。在评估误差类别准确率相近的情况下,对于没有准确评估的数据点,LSTM网络可能将较小范围的误差类别评估为较大范围的误差类别,使实际风电功率数据包含在评估区间范围内,IPICP会较高,反之IPICP会较低。

3.4 模型的性能评估分析

3.4.1 与其他模型的对比

本节通过对比BP,Elman 这2 种评估方法,分析LSTM 在基于误差分类的区间评估方面的性能。选取Elia 网站2017 年9 月至2018 年8 月的数据并以四季的形式划分,求得评估误差类别准确率Acc和评估区间覆盖率IPICP,见附录A 表A2 至表A9。以每个季节第1 个月份的Acc和IPICP结果为例,比较在不同季节、不同误差数据来源下3 种区间评估方法的性能。为了能更为直观地展示3 种评估方法的评估效果,选取基于Elman 预测误差的春季评估结果,引入分类混淆矩阵进行展示,见附录A 图A3。

由图A3 可知,本文所提区间评估方法对于每个类别的预测精度均达到0.9 以上,相较于Elman 和BP 评估,能更好地区分Ⅰ类误差和Ⅱ类误差,以及Ⅱ类误差和Ⅲ类误差,对于不同类别误差的识别和预测效果更好。

根据表A2 至表A9 可以看出,对于每种评估方法,误差数据来源不同,其区间评估评价指标值也就不同。整体LSTM 评估方式对于误差分类预测的准确性优于BP 和Elman,准确率最高的是对冬季Elman 误差类别的评估,达到0.998 0,同样情况下其IPICP也更高,为0.917 7。

BP 方法和Elman 方法均是利用神经网络学习风电功率和误差数据。除冬季基于AR 误差的评估以外,对其余季节的不同误差来源进行评估,这2 种评估方法均略逊于本文方法。BP 评估的评估误差类别准确率Acc最高只能达到0.947 6,对应的IPICP最高也仅为0.911 3。而Elman 评估结果最优的情况是对秋季Elia 误差类别的评估,Acc和IPICP分别为0.907 3 和0.846 8。对于LSTM 评估,其Acc都能达到0.74 以上。但在误差波动较大、功率与误差数据相关性较弱的情况下,BP 和Elman 的评估结果就会与本文方法得到的评估结果差距较大,比如对春季PER,AR 和Elia 误 差 类 别 的 评 估,BP 和Elman 的Acc均未达到0.7,且IPICP也相应较低。相较于BP 和Elman 这2 种评估方法,LSTM 中具有LSTM 单元,能关注到时间序列动态变化,更能捕获到时间序列上风电功率与预测误差的相关性,评估精度更高。

3.4.2 与基于概率分布的误差评估方法对比

本节通过与基于概率分布的误差评估方法作对比,分析LSTM 在基于误差分类的区间评估方面的性能。实际风电数据采用Elia 网站2018 年春季数据。利用t 分布和正态分布拟合误差的区间评估模型,得到置信度为90%的IPINAW和IPICP列于表1,本文方法得到的IPINAW和IPICP也列在表1 中。为了将本文方法与90%的置信区间结果相比较,表1 中还列出了将IPINAW增大1.1 倍和1.7 倍后的IPICP。为了分析本文方法在IPINAW扩大后的IPICP,以便从区间大小和准确性2 个方面分析对比本文方法和基于概率分布的评估方法,给出在IPINAW扩大1 倍至2.5 倍时的IPICP,如图4 所示。

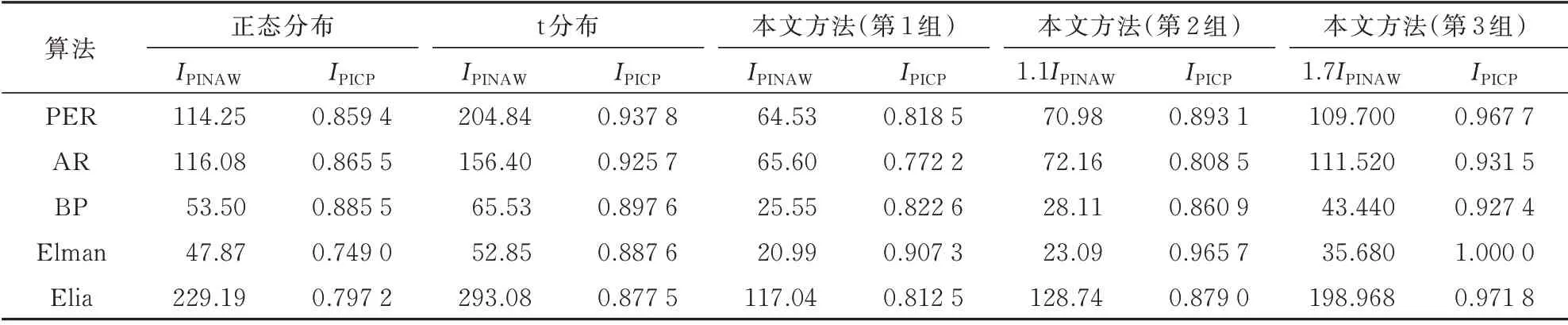
表1 不同方法下的IPINAW 和IPICPTable 1 Values of IPINAW and IPICP with different methods

图4 不同IPINAW 下的IPICPFig.4 Values of IPICP with different IPINAW

2 种拟合分布模型得到的IPINAW是本文所提评估方法的2～3 倍,但由于区间范围过窄使其IPICP略低于正态分布和t 分布的IPICP值。将由本文区间评估方法得到的IPINAW适当地增大一定倍数,可以使IPINAW在保持相对较小的情况下得到准确率更高的评估结果。当IPINAW扩大1.1 倍时,基于PER,Elman,Elia 这3 种误差的IPICP比使用正态分布拟合模型时更高,且IPINAW仍小于2 种分布拟合模型。当IPINAW扩大1.7 倍时,以对AR 误差进行区间评估为例,此时IPINAW为111.52（65.60×1.7=111.52）,与之对应的IPICP提高至0.931 5。根据表1,使用正态分布拟合模型时,IPINAW为116.08,IPICP为0.865 5；使用t 分布拟合模型时,IPINAW为156.40,IPICP为0.925 7。

由图4 可知,随着IPINAW的增大,IPICP也逐渐增大,区间评估结果的准确性随之提高。扩大倍数为1.7 以后,对于不同预测方法的预测误差,本文方法的评估精度最高达到100%,最低也达到92%以上,而其相应的评估区间带宽远小于基于概率分布的误差评估方法。因此,本文的区间评估方法可同时得到更小的区间覆盖率和更高的评估精度。减小区间覆盖率将降低电网调度时的备用裕量,而提高评估精度将降低风电的预测误差对电网发供用电平衡的冲击。

4 结语

针对风电预测误差数据的分布特性,本文提出一种误差分类的区间评估方法。首先,利用K-means 聚类对风电功率预测误差数据进行分类；再将风电功率和原始误差作为输入数据,误差类别作为输出数据,按照原时间序列顺序组成数据集,建立LSTM 评估模型得到评估区间。通过对比不同季节、不同误差数据来源的算例分析,以及通过与基于t 分布和正态分布的区间评估进行比较,可以得出基于误差分类的区间评估方法更为简便,能得到更加精确的评估效果,其评估精度不受拟合分布模型的影响,而且LSTM 相较于其他评估方法更能抓住风电功率和预测误差的联系。本文方法突破了原有区间评估方法的思路,提高了风电区间评估的准确性,为风电的电网规划、运行和安全稳定分析提供基础。但本文的区间评估针对的是历史风电功率和预测误差,如果增加输入数据,例如风速、风向以及气象等影响因素,有可能进一步提高区间评估精度。下一步可以研究综合考虑多种影响因素的区间评估方法。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。