考虑爬坡特性与预测区间优化的电热水器集群功率区间预测

余 洋，权 丽，贾雨龙，米增强，范 辉

（1. 河北省分布式储能与微网重点实验室（华北电力大学）,河北省保定市071003；2. 新能源电力系统国家重点实验室（华北电力大学）,河北省保定市071003；3. 国网河北省电力有限公司,河北省石家庄市050000）

0 引言

需求响应（demand response,DR）被认为是当下缓解电力供需矛盾、提高电网运行效率的有效措施之一［1］。作为柔性负荷重要一类的电热水器（electric water heater,EWH）,在与电网互动时具有储能容量大、响应快速等独特优势［2］。为了让EWH更好地参与需求响应调节,需准确预测未来一定时间段内的EWH 集群功率,以合理确定EWH 集群的中断时刻以及时长。

当前,关于EWH 集群功率的研究主要集中于建模、仿真与控制上［3-5］,对其进行预测的研究较为少见。研究发现［6-7］,用户使用EWH 具有一定的规律,而且EWH 集群参与需求响应运行一般是通过调整EWH 的温度限定值来实现,因此,EWH 集群功率在一定时间范围内会产生较大的波动,出现类似于风电功率的“爬坡”特性［8］,这给EWH 集群功率预测带来了巨大挑战。

传统电力负荷的点预测方法已较为成熟,预测精度不断提高［9］。负荷功率的单点预测仅能提供确定的预测值,而区间预测可进一步提供负荷波动风险预测信息［10］,构建有效的区间预测模型对EWH集群功率的不确定性度量更为必要。按照是否以点预测为基础,区间预测方法可分为以下2 类［11-13］。

1）基于点预测结果,采用人工智能或统计学等方法建立预测区间（prediction interval,PI）,此类方法区间预测精度在很大程度上取决于点预测的精度。如文献［14］提出了一种结合互补集合经验模态分 解（ensemble empirical mode decomposition,EEMD）、样本熵（sample entropy,SE）和改进相关向量机（relevant vector machine,RVM）的组合预测模型,能够得到质量较高的预测区间；文献［15］利用小波神经网络（neural network,NN）和二维核密度估计（kernel density estimation,KDE）提出了一种考虑爬坡特性的短期风电概率预测方法,具有较高的短期风电概率预测精度。

2）若不依赖点预测结果,可利用优化算法直接输出上下界。如文献［16］提出了一种利用上下界估计（lower upper bound estimation,LUBE）法构造预测区间的递归神经网络模型进行不确定性预测,并引入蜻蜓算法进行参数优化。不过这类算法较为复杂,使用时具有一定的局限性。

此外,系统中柔性负荷样本呈现海量特征［17-18］,且影响因素具有多源异构性［19］,使用过多的样本将增加系统运算压力,为此本文采用具有小样本处理优势的相关向量机［20］开展EWH 集群功率预测。但是针对EWH 集群功率的巨大波动特性,单一核函数的相关向量机鲁棒性较弱,尤其在发生“爬坡”事件时,将可能导致较低的预测精度。为此,本文引入多核相关向量机（multi-kernel RVM,MKRVM）来增强预测算法的鲁棒性,进一步提高预测精度,同时有效处理样本多源异构问题［21］。

鉴于第1 类算法简单、易实施［22］等特点,本文以第1 类算法为基础,在借鉴风电功率爬坡特性定义揭示EWH 集群功率波动性的基础上,提出了一种考虑爬坡特性和预测区间优化的MKRVM-KDE 组合区间预测方法。首先考虑影响EWH 集群功率的样本多源异构特征,构建了EEMD、主成分分析（principal component analysis,PCA）和MKRVM 相结合的高精度组合点预测模型,然后设计了一种KDE 与粒子群优化（particle swarm optimization,PSO）相结合的预测区间优化方法,同时采用渐近积分均方误差优化输出窗宽。本文算法能有效处理EWH 集群功率的爬坡特性,在保证期望预测区间覆盖率（prediction interval coverage probability,PICP）的同时,获得了宽度更窄的预测区间,提高了区间预测性能。

1 EWH 集群功率波动特性描述

1.1 爬坡特性的定义

由于风电功率的强随机性和波动性,风电功率有时会表现出爬坡特性［23］,目前国际上对于爬坡事件在数学上尚未形成统一的定义。设P(τ)和P(τ+Δτ)分别为τ 和τ+Δτ 时刻的负荷功率,这里引入2 种最常用的爬坡特性描述方法［24-25］。

1）若P(β)为设定的阈值,如果式（1）成立,则认为发生爬坡事件,对于P(τ+Δτ)-P(τ) ＞0,称为上爬坡事件；对于P(τ+Δτ)-P(τ) ＜0,称为下爬坡事件。

式（1）没有考虑爬坡的变化率,因而有了另一种定义。

2）若P(β′)为设定的阈值,ε(τ+Δτ)为爬坡率,判别式如下:

当式（2）满足时,就认为τ+Δτ 时刻发生了功率爬坡事件,爬坡率大小反映了此次事件的严重程度。

在对爬坡事件进行识别时,若阈值过大,易漏掉产生的爬坡事件；若阈值过小,则可能将较小的功率波动误判为爬坡事件。因此,需选取合理的阈值以提高EWH 集群功率预测精度［26］。基于获取的EWH 集群功率样本数据,参考现有文献中风电爬坡事件确定的阈值［27］,同时经过大量的实验,本研究中利用式（1）和式（2）检测爬坡事件的阈值为:上爬坡率大于600 kW/h（约为总功率的25%）,下爬坡率大于500 kW/h（约为负荷总功率的20%）。大量实验结果表明,本文选取的阈值能够对EWH 集群功率进行较为准确的爬坡事件识别。另外,值得一提的是,本文提出的预测算法本身具有一定的鲁棒性,对于一些小于阈值而没有被判定为爬坡事件的功率变化,本文算法也能够有效预测其波动。

1.2 EWH 集群功率的类爬坡特性分析

用户使用EWH 具有一定规律性,并且调度调控EWH 集群负荷时,需通过调整其温度限值来实现,这导致聚合大量用户的EWH 集群功率产生剧烈的波动［28-29］。为描述EWH 集群功率短时间内大幅度变化的现象,借鉴风电功率爬坡特性的定义,将其称为EWH 的爬坡事件。

1）短时间尺度下EWH 集群功率爬坡事件

依据热水器的参数分布特性,对智能小区EWH 负荷进行聚合［7］,可得某智能小区一天内的EWH 集群功率见附录A 图A1。图A1 表明,EWH负荷需求直接受用户热水使用情况影响,具有明显的时间特性,在热水使用高峰和低谷时段,负荷的波动较大,有着明显的突变特性。以15 min 为时间尺度,以式（1）定义下的爬坡事件确定准则进行分析,当P(τ+Δτ)-P(τ) ＞0 时会出现上爬坡事件,当P(τ+Δτ)-P(τ) ＜0 时会出现下爬坡事件。

2）长时间尺度下EWH 集群功率爬坡事件

根据式（2）定义的爬坡事件确定准则对较长时间下EWH 集群功率进行长时间尺度的识别。抓取某 智 能 小 区2017 年6 月15 日 至8 月15 日 的EWH 集群功率数据,取最小爬坡时间Δτ 为1 h,定义上爬坡率大于600 kW/h（约为总功率的25%）、下爬坡率大于500 kW/h（约为负荷总功率的20%）的功率变化为EWH 集群功率的爬坡事件。EWH 集群功率曲线和爬坡事件识别结果分别见附录A 图A2 和图A3。在图A3 中上半轴为上行爬坡事件,下半轴为下行爬坡事件,高度代表爬坡事件持续时间。由图A3 可知,EWH 集群功率在长时间尺度下也会存在爬坡事件,一旦有爬坡事件发生,传统预测算法下的预测误差将可能增加,预测高精度难以保证［30］。

3）EWH 集群功率爬坡特性分析

爬坡事件发生时段内EWH 集群功率表现出较大的波动性,不考虑EWH 集群功率的爬坡特性将可能给预测带来较大误差。为此,本文从2 个方面考量爬坡特性对EWH 负荷预测的影响,并给出应对方法以提高预测精度。第一,EWH 集群功率爬坡事件产生时,将呈现出极大的非线性和波动性,并伴随有噪声信号。拟使用EEMD 和PCA 对原始数据进行处理,将EWH 集群功率负荷序列有效处理为较规律、平稳性和低维度的新数据。第二,针对传统预测方法跟踪EWH 集群功率爬坡特性可能导致较大预测误差的问题,以高精度MKRVM 点预测结果为基础,考虑爬坡特性及其他不确定因素对误差分布带来的影响,采用KDE 法开展EWH 集群功率区间预测,获取高质量的预测区间,以提供更多的预测信息,降低系统运行风险。

2 相关理论论述

本文算法采用考虑爬坡特性的EEMD-PCAMKRVM-KDE 组合区间预测模型获得高质量的预测区间,其中的EEMD 和PCA 算法可参考文献［31-32］。

2.1 MKRVM

相 关 向 量 机［33］是2001 年 由Michael E Tipping提出的基于贝叶斯学习框架下的机器学习算法,该算法基于贝叶斯学习、马尔可夫性质以及最大似然估计理论,应用于回归预测具有独特的优势。EWH集群功率影响因素表现出了一定的差异性,通过不同的核函数建立多核函数来形成MKRVM,能有效处理数据的多源异构问题。常用的核函数中,高斯核函数适用于局部特性明显的样本,而多项式核函数适用于呈现出明显的全局性特征的样本。本文利用能量熵法获取EWH 集群功率影响因素的分布特点,在此基础上构造多核函数,具体如式（3）所示［34］。针对MKRVM 混合核参数的优化,本文采用粒子群优化算法［35］进行寻优。

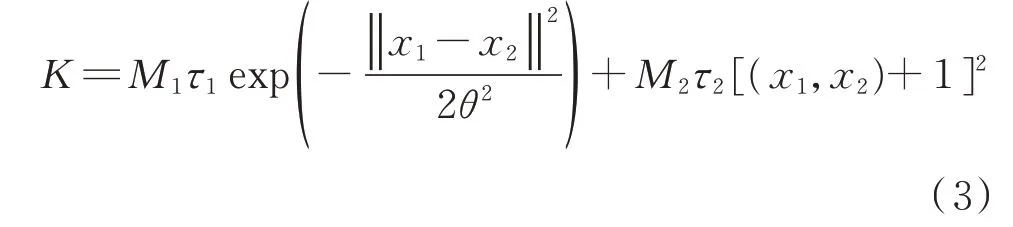
式中:τ1和τ2分别为高斯核函数和多项式核函数对应的系数；M1和M2分别为高斯核函数和多项式核函数的个数,M1+M2=M,M1τ1+M2τ2=1,多项式核参数为2,令κ1=M1τ1,其中κ1为高斯核函数的 权 系 数；θ 为 高 斯 核 宽 度 参 数；x1和x2为2 个 输 入变量。本文采用粒子群优化算法对MKRVM 核参数∂进行优化,其中∂包括θ和κ1。

2.2 KDE 法

KDE 法作为一种非参数估计法,能够直接提供概率密度函数,输出预测区间的上、下界。与参数估计法相比,它没有对数据分布进行任何假设,只是基于预测数据来构造区间,有着较高的可靠性。KDE法确定区间上、下界的具体过程请参考文献［36］。

3 基于EEMD-PCA-MKRVM 的点预测模型

3.1 样本分布的多源异构特性

EWH 集群功率主要影响因素有历史负荷、环境温度和爬坡事件序列等,而这些影响因素各自呈现出不同的特性,有的具有全局性,有的具有局部性,由此构成了EWH 集群功率影响因素的多源异构性。给定有M 个关于EWH 集群功率预测的影响因素,N 和T 均代表采样点数。输入变量序列为:{ Xi,i=1,2,…,M }, Xi=[ x1,x2,…,xN]∈R1×N,输出的负荷预测值Yi=[ y1,y2,…,yT]∈R1×T。由多核函数组成的MKRVM 能更有效地处理输入数据的多源异构特性,本文采用基于样本分布特征的能量熵法选择多核函数,多核函数的选择步骤如下。

判断样本分布特征的标准为:给定标准值为c*=0.5,若c ≤c*,则样本分布呈现全局性,宜采用多项式核函数；若c ＞c*,则样本分布呈现局部性,可采用高斯核函数。

3.2 组合点预测模型

在完成样本多源异构特性分析的基础上,本文设计了一种考虑爬坡特性的EEMD-PCA-MKRVM相结合的组合点预测模型完成EWH 集群功率预测,模型的运行流程可见附录A 图A4。该流程爬坡事件序列识别中,采用爬坡定义2 对EWH 负荷聚合功率发生的爬坡事件进行识别,组成爬坡事件序列,揭示了EWH 集群功率存在的爬坡特性。考虑负荷爬坡特性,选取高精度的MKRVM 组合预测模型进行点预测。点预测模型可分为数据预处理和负荷预测两大模块。数据预处理模块中将原始时间序列X(t)采用EEMD 进行分解,得到L 个本征模函数（IMF）；对IMF 分量采用PCA 降维处理,得到k 个主成分,然后利用特征向量进行PCA 重构得到新数据集x*(t)；在负荷预测模块中,将温度、相对湿度等因素和新数据集x*(t)共同作为输入变量进行MKRVM 回归预测,得到EWH 集总功率预测值y*。

本文采用平均绝对误差MAE和均方根误差RMSE这2 个 指 标 来 评 价 点 预 测 效 果［37-38］,计 算 公式为:

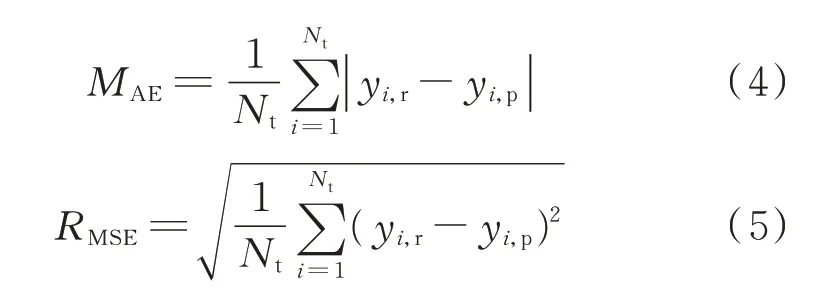
式 中:yi,r和yi,p分 别 为 第i 个 实 际 值 和 预 测 值；Nt为预测样本的数据个数。

4 预测区间的确定及优化

4.1 基于KDE 法确定预测区间

利用上述组合预测模型获取点预测值的同时,还能得到预测误差,然后直接利用KDE 法就可得到预测误差分布的概率密度函数,而不必对数据分布做出假设。本文即利用KDE 法来确定预测区间。在KDE 法中,核函数和带宽是2 个重要的参数。本文采用渐近积分均方误差来确定最优带宽,选取鲁棒性较好的高斯核函数作为核函数［39］。除了计算概率密度分布函数外,还要计算累积分布函数P:

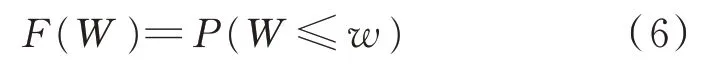
式中:F(W )为满足条件的概率；W 为用户侧负荷误差；w 为一定置信水平下的误差。

若累积偏差满足式（6）,则认为能够满足用户侧负荷预测要求。给定置信度α′,则置信水平为（1-α′）,F( α′ 2 )和F(1- α′ 2 )能够从式（5）确定。因此,对于某个预测值yi,给定具体的置信度α′,就能够得到预测区间的上、下界,描述如下:

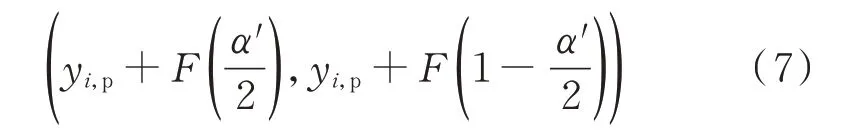
4.2 预测区间的多目标优化

4.2.1 区间预测的评价指标

1）期望预测覆盖率。可靠性被定义为期望预测覆盖率和给定置信水平的一致,通常采用期望预测覆盖率PICP来评估区间预测的可靠性,其定义为:

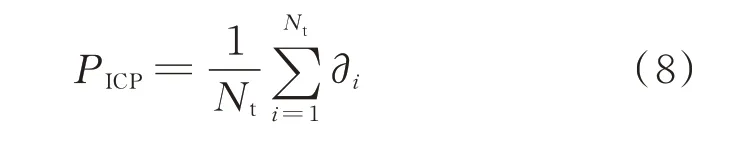
式中:∂i为布尔量,当目标值落在区间内时为1,当目标值落在区间外时为0。

2）区间宽度指标。在满足可靠性的同时,更窄的区间宽度能够提供更为精确的预测信息,这也是3.2 节研究意义所在。通常采用2 个指标评估区间宽度［40］,即区间平均宽度PINAW和累计宽度偏差AWD,计算公式分别见式（9）和式（10）。累计宽度偏差作为衡量相对偏差程度的一个指标,能够评估真实值落在区间外的概率,其值越小,区间相对偏差越均衡,预测区间的质量越高,该指标可由第i 个样本的累计宽度偏差AWDi之和得到,其中AWDi见附录A式（A1）。

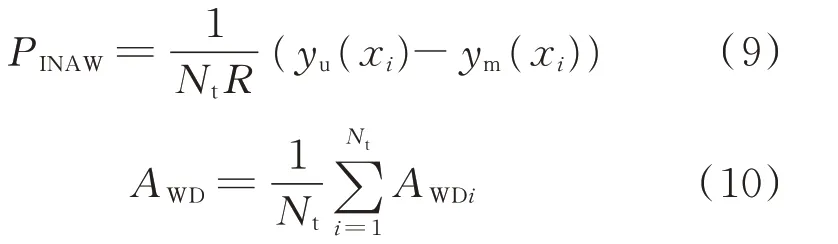
式中:yu(xi)和ym(xi)分别为区间的上界和下界；R为预测目标值的变化范围（最大值与最小值之差）。

4.2.2 优化目标函数的构建

期望预测覆盖率、区间平均宽度和累计宽度偏差可从可靠性、清晰度和相对偏差3 个方面来衡量预测区间的质量,期望预测覆盖率越大,区间平均宽度和累计宽度偏差越小,获得预测区间的质量越高。因此,可通过最大化期望预测覆盖率以及最小化区间平均宽度和累计宽度偏差来得到高质量预测区间,这也可以认为是一个多目标优化问题。本文采用粒子群优化算法,寻找能同时考虑这3 个评价指标的最优区间,将多目标问题转化为单目标优化问题,来优化MKRVM 的核参数以获得更高质量的预测区间。

为获得最小化目标函数,定义期望预测覆盖率的等价指标预测覆盖率偏差ACE=PINC-PICP,即期望预测区间置信水平（PI nominal confidence,PINC）与期望预测覆盖率之差。因此,为获得较理想的预测区间,结合ACE、区间平均宽度和累计宽度偏差,共同构成了综合目标优化函数如下:

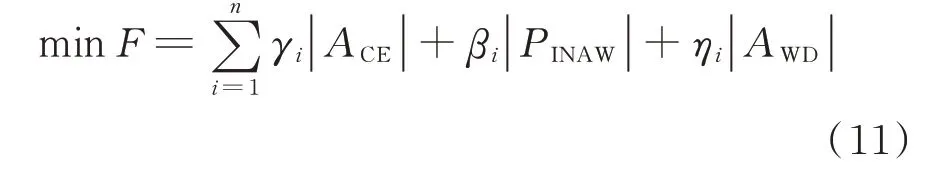
式中:γi,βi,ηi分别为期望预测覆盖率偏差、区间平均宽度和累计宽度偏差的权重系数；n 为迭代次数。

4.3 区间预测具体实施步骤

考虑爬坡特性的EWH 集群功率组合区间预测方法的总体框图如附录A 图A5 所示,根据该框架,区间预测的具体实施步骤如下。

步骤1:利用能量熵法分析样本分布特性,确定MKRVM 多核函数。

步骤2:对原始序列采用EEMD 和PCA 完成数据预处理,得到EWH 集群功率重构信号,同时考虑温度和相对湿度等因素,基于附录A 图A4 开展点预测,其中,利用粒子群优化算法寻优,确定MKRVM 混合核参数的最优值。

步骤3:基于点预测得到的预测误差,实施非参数KDE,得到累积分布函数。

步骤4:利用式（7）计算得到区间预测的上、下界,获取高质量预测区间。

5 算法验证

5.1 数据集选取

选 取 某 智 能 小 区2017 年6 月15 至2017 年8 月15 日的EWH 集群功率数据作为样本集,一天分为0～23 h 共24 个时刻,每小时监测一次,同时综合考虑温度、湿度等因素对EWH 集群功率的影响,将这些因素与历史功率数据共同作为训练数据。为了更好地验证本文预测方法的性能,将本文方法与现有相关向量机方法进行比较。

5.2 模型参数设置

yu(xi)和ym(xi)初始值分别设置为预测目标值上下浮动25%。粒子群种群个数为90；学习因子为2；惯性权重因子为0.7；迭代次数为100；MKRVM含有2 个核参数,即混合核参数为∂=(θ,κ1),各权重系数的值取为:γi=1,βi=2,ηi=0.1。经过粒子群优化迭代后得到最优混合核参数为∂b=(0.612,0.921)。

5.3 点预测结果及分析

1）数据预处理

对原始负荷序列进行EEMD,得到IMF 分量,其中一部分IMF 分量的EEMD 分解结果如附录A图A6 所示,IMF1 为原始柔性负荷数据,可以看出原始数据具有非平稳、复杂的特性。经EEMD 后,IMF2 和IMF4 的波动性较 大,IMF5 和IMF8 的波动性相对较小,最后一个分量rm为剩余分量。

将剔除原始数据后的12 个IMF 分量进行PCA降维得到5 个主成分,主成分的特征值和贡献率以及累计贡献率见附录A 表A1。由表A1 可知,前5 个主成分的累计贡献率为90.54%,超过了85%,达到了选取主成分的要求,故可用主成分代表原始数据。

2）考虑爬坡特性的组合点预测结果

针对7 月26 日至7 月29 日间EWH 集群功率负荷样本数据,利用式（2）对EWH 集群功率进行爬坡事件的识别。EWH 集群功率爬坡事件识别结果见附录A 图A7。结果表明,7 月26 日11:00,14:00 和23:00,7 月27 日12:00 和17:00,7 月28 日11:00 和23:00,以 及7 月29 日12:00 和21:00 等9 个 时 刻 均发生了爬坡事件。传统预测算法针对较小的负荷变化有着良好的鲁棒性,而当发生爬坡事件时,EWH呈现出较大的波动性,这在一定程度上会降低预测精度。本文算法则具有良好的爬坡事件识别性。

为体现本文算法在提高点预测精度方面的优势,选择单核相关向量机组合预测算法作为比较算法与本文算法进行比较。利用该智能小区7 月22日至7 月25 日的EWH 集群功率作为训练样本、7 月26 日至7 月29 日的EWH 集群功率作为测试样本来进行验证。图1 给出了比较预测曲线,表1 为预测精度比较结果。

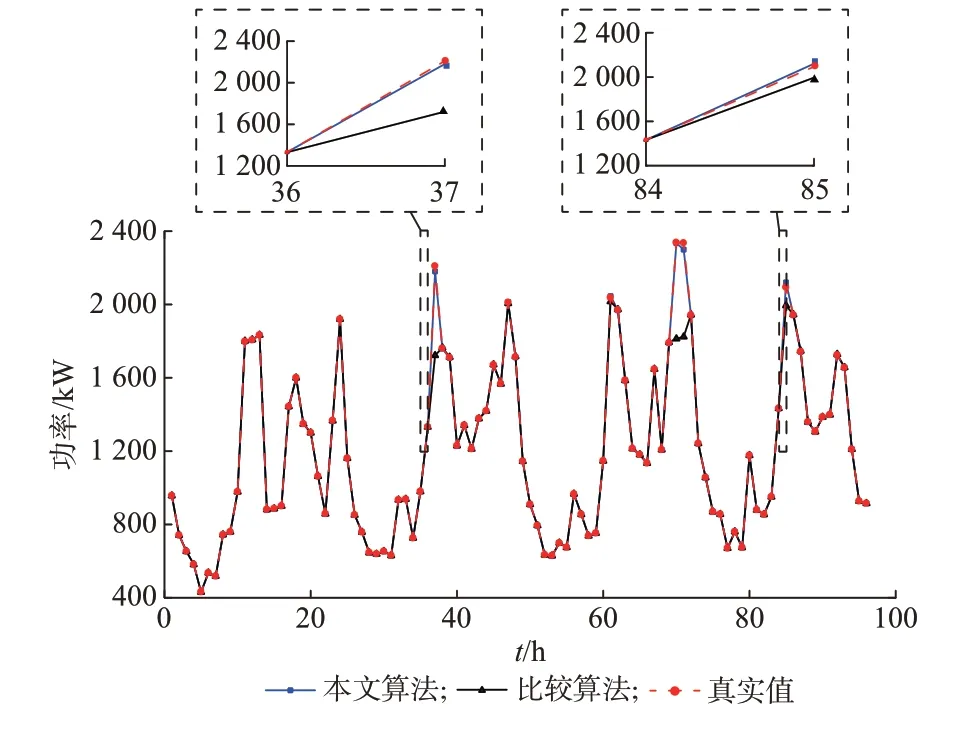
图1 EWH 集群功率预测曲线Fig.1 Prediction curves of aggregated power for EWH

表1 预测算法的均方根误差及平均绝对误差比较Table 1 Comparison of root-mean-square error and mean absolute error for prediction algorithms

可知,针对夏季智能小区EWH 负荷短期预测,爬坡事件和温度等因素有着重要的影响。由于7 月26 日11:00 和14:00、7 月27 日12:00 和7 月29 日12:00 均发生了爬坡事件,负荷突变导致比较算法无法准确预测负荷波动,而本文算法能较好地跟踪负荷变化。这是由于比较算法鲁棒性较弱,受爬坡特性影响较大,部分拟合预测过程偏差较大,导致预测精度较低。综合考虑温度、爬坡事件等因素的组合预测模型有着更好的泛化能力和鲁棒性,能够有效提高预测精度。

5.4 预测区间的确定

获得了良好的点预测结果之后,给定置信水平为80%,利用预测误差、KDE 法以及正态分布,得到集群功率误差频率分布直方图和概率密度函数,见附录A 图A8。可知,与正态分布和Gumbel 分布相比,KDE 法能够很好地描述负荷误差的变化,不仅能够跟踪上误差峰值,具备良好的平滑度和精度,还能够提供基本的误差数据分布特征。

为进一步分析带宽对KDE 平滑度和精度的影响,采用渐近积分均方误差法对不同窗口宽度进行模拟,结果见附录A 图A9,可知在带宽为5 时,有着更好的平滑度和精度,故最佳带宽确定为5。

5.5 区间预测结果及分析比较

为了提高电力系统调度运行的可靠性和稳定性,对区间预测的精度提出了一定的要求,需给定较高的置信水平来得到较高的期望预测覆盖率。本文选取80%,90%,95% 这3 种置信水平对此进行验证。

为了进一步说明本文算法能够提供高质量预测区间,选取EEMD-PCA-MKRVM 组合区间预测模型和EEMD-PCA-RVM-KDE 组合区间预测模型这2 种方法分别作为比较算法1 和比较算法2 进行对比分析。

首先,在同样采取考虑爬坡特性的高精度MKRVM 组合预测点预测的基础上,将本文算法和比较算法1 进行EWH 集群功率区间预测比较,结果见图2。经计算得到的2 种算法区间预测评价指标如表2 所示。MKRVM 利用分位数、均方差计算得到区间的上、下限,公式见附录A 式（A2）和式（A3）。

与比较算法1 相比,在同样采取考虑爬坡特性的高精度MKRVM 组合点预测的基础上,本文基于粒子群优化的MKRVM-KDE 组合预测模型来构造预测区间,能够更好地跟踪EWH 集群功率的变化,在一定的置信水平下,有更小的预测覆盖率偏差和更窄的区间宽度。

为了说明考虑爬坡特性对区间预测产生的影响,采用不考虑爬坡特性的比较算法2,取95%置信水平下对EWH 集群功率进行区间预测,结果如图3所示。由图2（c）和图3 可知,考虑和不考虑爬坡特性下期望预测覆盖率分别为96.39%和93.47%。结果表明,考虑爬坡特性后能够有效提高点预测精度,在一定置信水平下提高期望预测覆盖率。

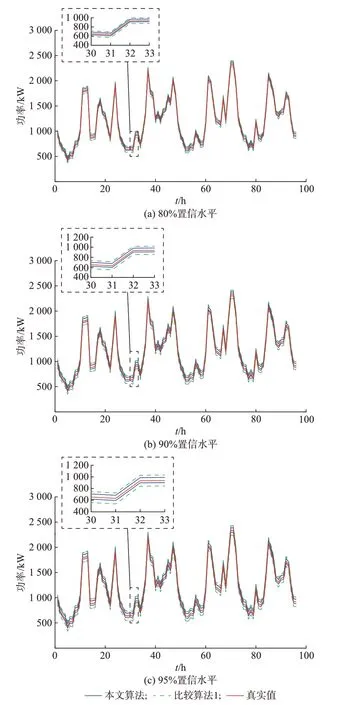
图2 不同置信水平下区间预测结果比较Fig.2 Comparative results of interval prediction with different confidence levels

表2 区间预测评价指标Table 2 Evaluation indices of interval prediction

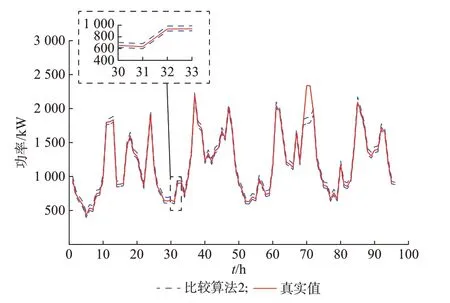
图3 不考虑爬坡特性95%置信水平下的区间预测结果Fig.3 Interval prediction results at 95% confidence level without considering ramp characteristics

由于预测误差对预测区间构造有重要的影响,考虑爬坡特性的组合预测模型有效提高了预测精度,减小了预测误差,有利于进一步优化区间。但是常规MKRVM 组合预测模型进行预测区间构造的方法,只是在一定置信水平下提高了期望预测覆盖率,却使得区间宽度变得更大,得到的预测区间不是很理想。而利用本文算法得到的预测区间,在满足期望预测覆盖率的情况下,区间宽度更窄,质量也更高。

6 结语

针对EWH 集群功率的波动性,提出了一种考虑爬坡特性和预测区间优化的EWH 集群功率短期区间预测方法,研究结论如下。

1）与EEMD-PCA-RVM 组合预测算法相比,考虑爬坡特性和样本特征的EEMD-PCA-MKRVM组合点预测方法的鲁棒性更好,预测精度更高,可行性更强。

2）利用粒子群优化算法优化MKRVM 参数,同时采用渐近积分均方误差优化KDE 法窗宽,使得MKRVM-KDE 结构能够提供更好的区间预测性能。

在利用MKRVM 提高鲁棒性和有效处理多源异构数据优势的同时,预测速度会有所下降。在后续研究中,可采用基于MapReduce 并行化方法提升MKRVM 的预测速度。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。