负荷聚合商模式下考虑需求响应的超短期负荷预测

郭亦宗，冯 斌，岳铂雄，郭创新，潘 军，朱以顺

（1. 浙江大学电气工程学院,浙江省杭州市310027；2. 广东电网有限责任公司广州供电局,广东省广州市510600）

0 引言

需求响应（demand response,DR）技术能够充分挖掘用户侧资源,引导用户主动参与电力市场运营与调控,也为电力系统的削峰填谷起到了较大的促进作用,是推动能源互联网建设的关键技术之一［1-2］。随着电锅炉等能量转换设备和储能技术不断提高,有关需求侧的研究不再仅仅面向电力负荷的DR,而是包含多种形式负荷、储能、分布式电源的DR［3］。DR 资源的分散性较强,其弹性水平往往达不到电网DR 的要求,难以单独与DR 购买者进行双边交易,且单一用户的决策无法满足DR 的管理和优化要求［4］。因此,有学者提出负荷聚合商（load aggregator,LA）这一商业模式,旨在整合分散的DR资源,统一调控［5］。

LA 作为连接DR 资源购买者与DR 资源的中介,是DR 得以实施的有效途径,而DR 则是LA 参与电力市场获得收益的主要方式［6］。一般来说,LA通过与用户签订DR 合同来实现需求侧管理,对用户的柔性负荷具有一定的控制权［7］。LA 为追求收益最大化,通过DR 改变用户的原始用能行为,从而影响负荷的变化趋势,现有的超短期负荷预测方法无法很好地反映LA 决策,因此研究在LA 模式下的超短期负荷预测具有必要性意义［8］。同时,在LA 模式下进行超短期负荷预测是LA 制定发电计划、调度计划以及研究DR 弹性的基础,具有重要意义［9-10］。

国内外诸多学者对超短期负荷预测的方法做了较多研究,但较少在LA 模式下考虑DR 的影响,其预测结果不能很好地服务于LA 模式的后续研究［11-13］。文献［14］建立了基于Logistic 函数的用户模糊DR 机理,将DR 因素引入径向基函数（RBF）神经网络模型进行超短期负荷预测；文献［15］对计及LA 模式的DR 进行建模分析,并引入到RBF 神经网络模型进行超短期负荷预测,但是未考虑分布式电源、用户侧储能、可控热负荷以及用户参与DR 的不确定性。也有学者在负荷预测的算法上进行改进,文 献［16］将 长 短 期 记 忆（long short-term memory,LSTM）网络应用于负荷预测,验证了在DR 影响下该模型的预测精度更高；文献［17］对LSTM 方法进行了改进,利用卷积神经网络提取特征向量以达到更高的预测精度；文献［18］提出深度LSTM 模型应用于超短期负荷预测,适用于离线训练实时预测；文献［19］提出了基于Attention-LSTM的超短期负荷预测模型,利用负荷的时序特性,改进预测精度。

为更好地预测LA 模式下的负荷变化,本文首先分析LA 模式下的DR 机制,并进一步考虑用户用能习惯、用户自建光伏、用户储能行为以及电热耦合,建立可中断电负荷（interruptible load,IL）、可转移电负荷（transferable load,TL）、光伏储能单元以及供暖型热负荷（heating load,HL）的DR 信号模型,并建立用户参与DR 的不确定性模型；然后提出不计及DR 信号和计及DR 信号的LSTM 网络负荷预测模型,并选取实施LA 模式的某地区实际负荷数据进行算例分析。调用CPLEX 求解DR 信号并作为预测输入的一部分,预测结果验证了LA 模式的可行性和计及DR 信号的LSTM 负荷预测模型具有更好的预测性能,并且考虑DR 不确定性后预测精度将进一步提高。

1 基于LA 模式的DR 信号模型

LA 模式存在着DR 行为,LA 具有一定程度的负荷控制权,能够根据与用户签订的双边合同对负荷进行削减或转移、对储能进行放电或充电,这一行为影响着负荷的未来变化趋势。因此,在LA 模式下进行负荷预测需要充分考虑LA 参与DR 的决策行为,体现在预测网络上则是增加了LSTM 的输入量。

本文立足于LA 模式建立各类DR 资源的DR信号模型,并将合成DR 信号作为LSTM 的一个输入量,改进训练网络。所谓DR 信号,即LA 以收益最大为目标所优化得到的各时段负荷削减或转移量、储能放电或充电量。

建立基于LA 模式的DR 机制,如图1 所示。

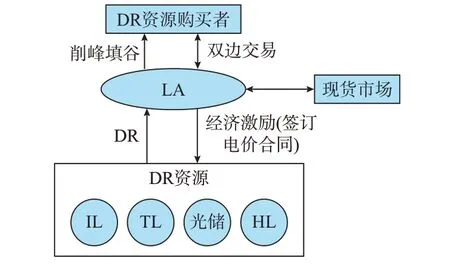
图1 基于LA 模式的DR 机制Fig.1 DR mechanism based on LA mode

LA 模式主要包含3 类参与者,分别为DR 资源购买者、LA 和DR 资源。其中,DR 资源购买者包含发电商、电网公司、售电公司等,可与LA 形成双边交易,通过设定合同激励价格促进LA 参与DR［20］。LA 是以盈利为目的的中介公司,利用先进的通信和互联网技术聚合各类DR 资源,响应购买者削峰填谷的需求并获得其提供的经济报酬［7,21］。DR 资源是具有DR 潜力的用户,根据负荷性质、DR 能力、各元件的组合特性划分为4 类DR 资源,分别为:IL、TL、光伏储能单元和HL。所有参与DR 的用户与LA 签订电价合同,合同规定了一日内的DR 时长、响应功率总额、合同定价等内容。用户将自身用电计划的部分决策权交于LA,为LA 响应DR 资源购买者的需求提供保障,相应会获得由LA 支付的经济奖励。同时,合同还规定了违约的惩罚机制,以降低不确定性的影响。

在实际运行中需要考虑供暖型热负荷的能量供应是由电锅炉通过电-热转化而得到的。因此,本章将在LA 模式下建立4 种DR 资源的优化模型和电锅炉的数学模型,求解各DR 子信号。

1.1 IL 的DR 子 信 号

合同激励价格在不同时段是不一样的,在负荷高峰时段价格较高,能够有效促进IL 主动削减,以降低系统在用电高峰时的功率平衡压力,延缓输电线路建设。本文在LA 模式下进行负荷预测,LA 负责行使DR 的控制权,需要以LA 为主体,对区域内所管理的IL 进行用电计划优化。因此,以LA 盈利最大为优化目标,IL 的DR 子信号优化模型为:

式中:Pmax和Emax分别为合同规定的负荷最大削减功率和一日内最大削减电量；Δt 为时段间隔。

LA 模式下用户削减负荷的持续时间受到限制,若持续时间太长,将会降低用户满意度,若持续时间太短,常无法满足电网DR 的要求。因此,需要限制DR 的持续时间。同时,从用户削减负荷的心理角度考虑,用户不希望多次削减负荷,而是期望在一日内至多有一次连续削减。

1.2 TL 的DR 子 信 号

TL 是通过实时电价的指导作用,主动引导用户将高峰电价时段下的部分电负荷转移到低谷电价时段使用,保证一日内负荷总量不变。LA 模式下,对于TL 用户的DR 调度方式与IL 用户相似,目标函数也一致,故在此不再赘述。然而,整体的约束条件略有不同,具体列出如下:

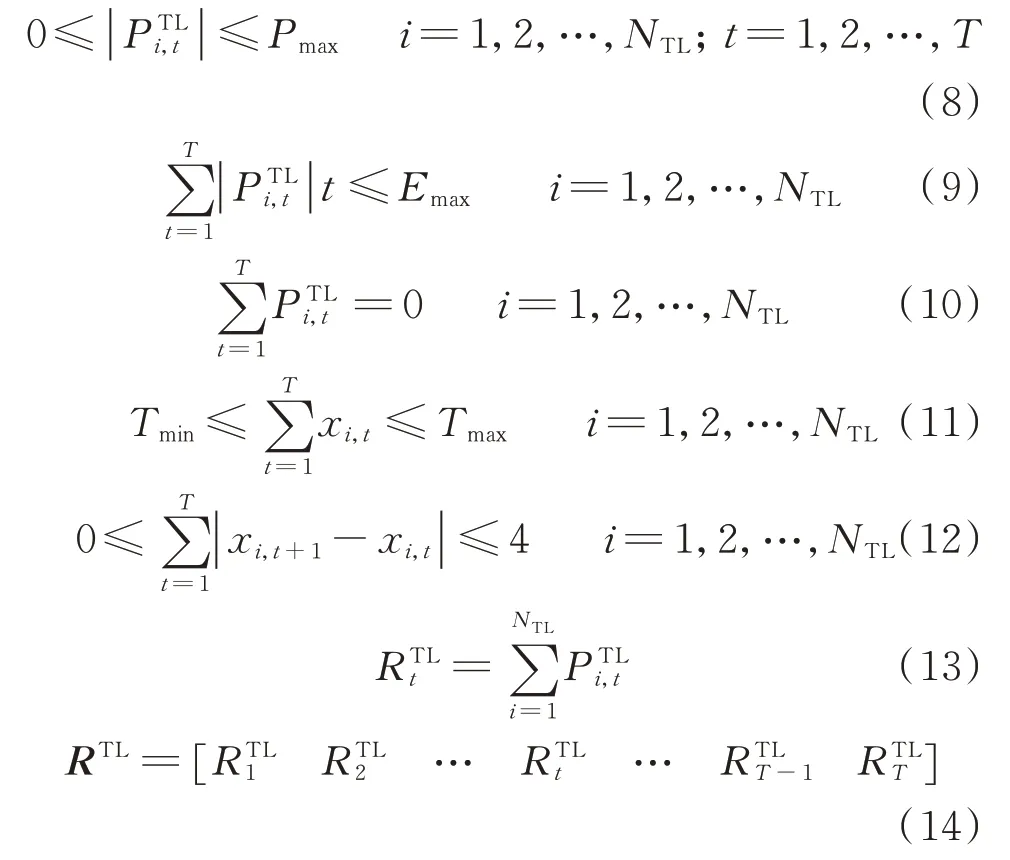
1.3 光伏储能单元的DR 子信号

光伏等分布式电源和储能都是LA 模式下DR的重要资源,两者往往组成光储单元联合调度［22］。本节考虑用户的储能行为,建立此场景的能源集线器结构如附录A 图A1 所示。

结合能源集线器结构,单一光储单元用户期望的充放电行为分析如下:当供给光储单元用户i 的光伏出力PPVi,t大于固定负荷PFLi,t或t 时段电价为低谷电价时储能充电；当用户光伏出力PPVi,t小于固定负荷PFLi,t且t 时段电价为高峰电价时储能放电。

结合附录A 的推导分析过程,得到光储单元用户在每一时段充放电行为的数学模型如下:

式中:δ 为储能设备的自放电率。

1.4 HL 的DR 子 信 号

在室内的舒适温度范围内,温度的小幅度变化不会影响人体感官的舒适程度。因此,LA 可以在确保用户满意度的前提下与HL 用户签订DR 合同。本文采用基于电路模拟的等效热参数方法建立建筑物一阶热力学模型,反映热负荷与室内温度的关系［23］。

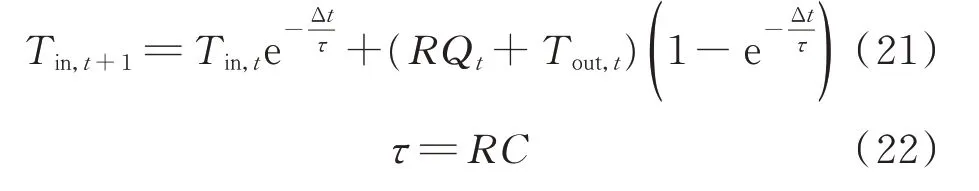
式中:Tin,t+1和Tin,t分别为t+1 和t 时刻的室内温度；Tout,t为t 时刻的室外温度；R 为建筑物等效热阻；C 为室内空气的比热容；Qt为t 时刻的热负荷。

式（21）和式（22）变形后得到削减后的热负荷Q1,t及削减的热负荷量ΔQt:

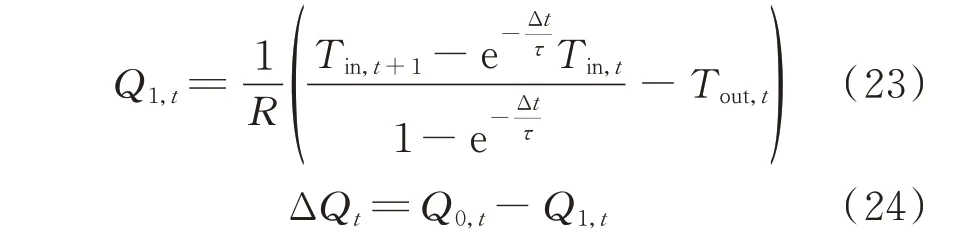
式中:Q0,t为削减前t 时刻的热负荷。

热负荷的削减伴随着温度的下降,为保证用户的舒适度,温度下降有一限值,满足如下约束:

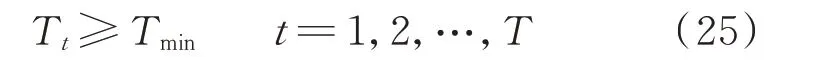
HL 的温度削减过程与IL 相似,其DR 子信号优化的目标函数也相似。

1.5 电锅炉能量转换模型

本文中电锅炉的输入端连接配电网节点,输出端连接HL,实现了热负荷参与系统DR。因此,需要建立电锅炉的能量转换模型,具体如下:

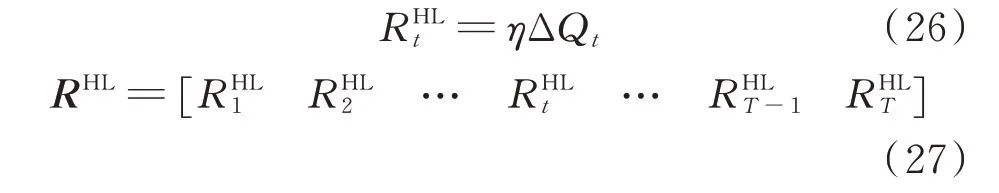
1.6 DR 信号的合成

计算上述4 个DR 子信号,通过叠加形成DR 信号并输入LSTM 的输入层。

式中:R 为LA 聚合后的DR 信号。

为更清晰地凸显DR 信号的构成及特点,通过图例加以展现,如附录A 图A2 所示。

1.7 用户DR 的不确定性

考虑到用户用电的不确定性,在面对突发事件或该时段用电能够带来更大收益的情况下,用户宁愿支付一定数额的违约金而选择拒绝响应。基于消费者心理学,用户削减或转移负荷的响应率与经济激励的大小呈正相关,经济激励越大,用户响应率也越大,并在某一经济激励下达到饱和。图2 为用户参与DR 不确定性的规律,其中响应率可用乐观和悲观情形下的线性函数λmax( p)和λmin( p)描述,能够满足工程要求［24］。

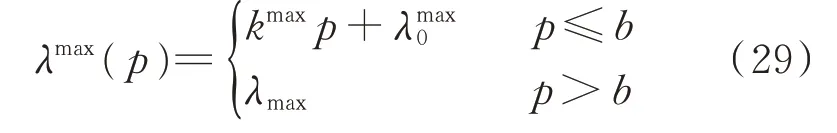
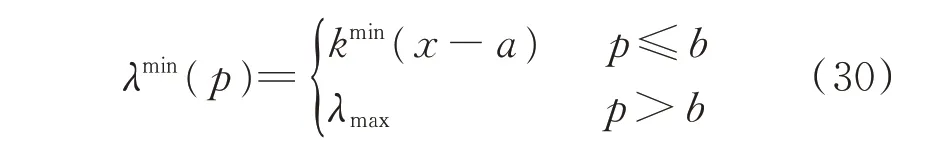
式中:p 为经济激励；kmax和kmin分别表示乐观和悲观情形下的响应率曲线斜率；a 和b 分别为临界激励和饱和激励；λmax0为无激励条件下用户的自身最大响应率；λmax为用户能达到的最大响应率。

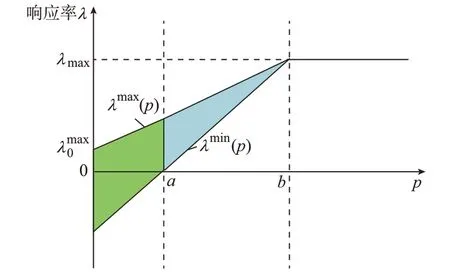
图2 用户DR 不确定性机理Fig.2 DR uncertainty mechanism of user

经济激励为0 时,用户响应率只受用户自身响应意愿的影响,随着经济激励的增大,具备响应潜力的用户会倾向于响应削减指令,响应率期望增加,波动范围减小；当经济激励增大到饱和值时,用户响应率达到最大值且波动范围可近似忽略。

针对经济激励下的响应率不确定问题,现有的研究多以模糊参数来表征,且采用三角隶属度函数描述模糊参数更符合DR 项目实际［25-26］。建立三角隶属度函数如下,其函数图像见附录A 图A3。

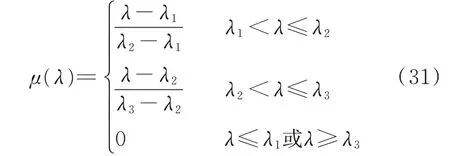
式中:λ1,λ2,λ3均为隶属度参数。

隶属度函数值越接近1,则用户DR 的不确定程度越大,反之则越小。某一经济激励下的响应率是从悲观情形到乐观情形的一个范围,且随着λ 的增大,不确定程度表现为先增大后减小,反映出用户DR 不确定性。

2 超短期负荷预测

2.1 LSTM 模型

循环神经网络可以解决传统神经网络不能持续记忆的问题,允许之前的信息保留一段时间,其记忆特性适用于超短期负荷预测。但是循环神经网络在输入序列较长时存在长期依赖问题。因此,文献［27］提出LSTM 以解决此问题。LSTM 是循环神经网络的一种变体,也是链式结构,但是重复模块有所差异,标准循环神经网络的重复模块内只有一个神经网络层,而LSTM 有4 个网络层,它们以一种特殊的形式交互。

LSTM 的核心是引入了一个新的单元状态,在传递线性循环信息的同时输出信息给隐藏状态,如图3 所示贯穿整个重复结构的水平线就是单元状态。图 中,σ 和tanh 分 别 代 表sigmoid 和tanh 激 活 函数,xt为输入量,ht和ht-1为当前和上一时间步的隐藏状态,Ct和Ct-1为当前和上一时间步的单元状态,it,ft,ot分别为当前时刻的输入门、遗忘门和输出门。

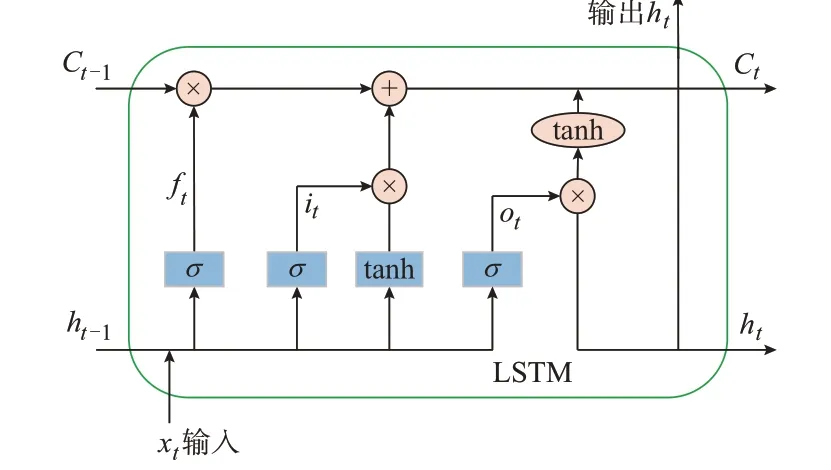
图3 LSTM 网络结构图Fig.3 Network structure of LSTM

LSTM 通过3 个控制门单元（输入门、遗忘门、输出门）选择保留或者忘记信息。式（32）形成了当前时刻的单元状态,式（33）形成了当前时刻的隐藏状态,式（34）表示输入门控制当前时刻的输入信息有多少需要保留；式（35）表示遗忘门控制上一时刻的信息需要丢弃多少；式（36）表示输出门控制当前时刻有多少信息需要输出给隐藏状态ht。LSTM 网络每一时间步的状态更新公式如下:

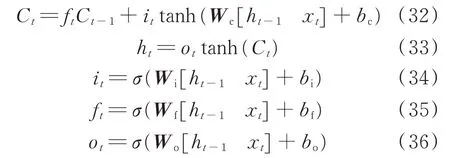
式中:W 为权重矩阵；b 为偏置常数；下标c,i,f,o 分别表示单元状态、输入门、遗忘门和输出门。

LSTM 有能力删除或增加神经元状态中的信息,这一机制被称为门限的结构精心管理。门限是以sigmoid 函数为激励函数的前馈神经网络,本质上是一种让信息选择性通过的方式,通过sigmoid 神经网络层和逐点相乘器形成。使用sigmoid 函数的原因是其输出在［0,1］区间,可以等效为一组权重值。当输出值为0,门限将遗忘所有信息；当输出值为1,门限将保留所有信息。

因此,LSTM 选择性遗忘或保留的能力能够有效解决标准循环神经网络在序列信息过长时面临的梯度弥散或梯度爆炸问题,有利于序列信息建模。

2.2 基于LSTM 的超短期负荷预测

2.2.1 不计及DR 信号的超短期负荷预测

不计及DR 信号时,输入数据只有历史负荷数据,输出数据为下一时间点的预测数据。预测的负荷时间间隔与输入负荷数据的时间间隔一致。

超短期负荷预测时采取迭代负荷预测的方法。所谓迭代预测指每次均根据若干个历史数据点预测下一个时间点的负荷数据。举例说明,根据09:00,10:00,11:00,12:00 这4 个时刻的负荷数据,预测13:00 的负荷数据,在下一次预测时,将13:00 的真实历史负荷数据连同10:00,11:00,12:00 共4 个时刻的历史负荷数据一起输入至神经网络模型中预测得到14:00 的负荷预测值。不计及DR 信号的模型输入如附录B 图B1 所示。

网络的损失函数是均方误差（MSE）函数式:

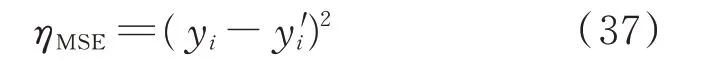
式中:ηMSE为均方误差；yi为功率真实值；y′i为功率预测值。

2.2.2 计及DR 信号的超短期负荷预测

计及DR 信号后的模型输入及分析如附录B 图B2 和图B3 所示。在考虑DR 信号后,模型输入的历史数据为过去4 个时间点的负荷数据以及与之对应的4 个DR 信号构成的2×4 矩阵,模型的（标签）输出值仍然为下一个时间点的负荷数据。此外,模型输入数据的变化将导致参数维度变化,但模型结构仍然不变。

对于输入数据的预处理过程,不仅需要对负荷数据归一化,还需要对上文由CPLEX 求解器求得的DR 信号进行归一化处理,消除信号之间量纲和数值大小的差异。预测方法与不计及DR 信号的相同,也采用迭代负荷预测方法。

需要说明的是,本文还探讨了用户参与DR 的不确定性对超短期负荷预测的影响,考虑这一因素仅会改变输入的DR 信号数值大小,不改变预测的模型结构和预测方法,在此不再赘述。

2.2.3 LA 模式下LSTM 超短期负荷预测流程

上述预测过程中,DR 是伴随LA 模式而存在的,在LA 模式下进行负荷预测时需要考虑其影响进而提高预测精度。流程图及分析如附录C 图C1。

2.3 预测评价指标

本文的预测评价指标选取为均方根误差（RMSE）和平均绝对百分比误差（MAPE）,如式（38）和式（39）所示。RMSE 与MAPE 的值越接近0,预测误差越小,模型的预测效果越好。

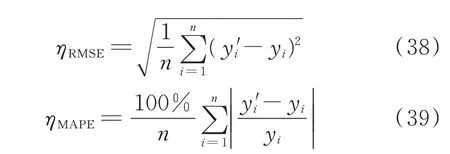
式 中:ηRMSE和ηMAPE分 别 为RMSE 和MAPE 的 指标值。

3 算例分析

本算例分析LA 模式下DR 信号对超短期负荷预测的影响,并探究用户参与DR 的不确定性在改善预测效果的作用。首先,利用LA 与用户签订的合同以及某地区电网实际数据计算上文各DR 资源子信号。然后,将DR 总信号引入LSTM 网络模型,设计了3 种预测场景,对比3 种场景下的负荷预测值与真实值。最后,分析LA 模式下的DR 信号和用户参与DR 的不确定性对超短期负荷预测精度的影响。

3.1 DR 总信号求解

本算例选取美国PJM 市场下LA 和用户的合同数据,如附录D 表D1 所示,DR 资源购买者提供给LA 的合同激励价格如附录D 图D1 所示。DR 资源包含HL,选取北方某地冬季一日内的室外温度为数据,如附录D 图D2 所示。建筑物的等效热阻R=18 ℃/kW,空 气 的 等 效 比 热 容 C=0.525(kW ⋅h)/℃,电锅炉电热转换系数η=0.90。DR 不确定性是通过改善DR 信号从而提高预测精度的,根据上文建立的模糊参数响应率模型,参考文献［24-26］并进行调研,算例基于合同约定的用户最大响应功率,设定无激励下的最大响应率为10%,饱和激励时用户能达到的最大响应率为95%,临界激励和饱和激励分别为合同电价的1 倍和1.25 倍。模糊表达的响应率介于乐观情形和悲观情形之间,描述用户的真实响应情况,其时间尺度与下文负荷预测时间尺度一致。

需要说明的是,在LA 模式下,LA 与系统运营商之间也会签署双边合同,若LA 因用户违约无法满足系统运营商的合同需求,系统运营商将安排发电机组多发电以补足负荷功率。因此,本文为分析方便,设定LA 与系统运营商、LA 与用户之间的违约惩罚成本均为上网电价。

分别求解不考虑DR 不确定性与考虑DR 不确定性2 种情况下的DR 信号,如附录D 图D3 所示,且得到各DR 资源最优收益情况如附录D 表D2 所示。

不确定性能够进一步反映用户真实的响应情况。对比2 种情况分析,不考虑用户DR 的不确定性时,DR 信号取得理想下的最大值；考虑用户DR 的不确定性后,由于用户存在违约的可能,各时段的DR 信号均有所减小。

无论是否考虑DR 的不确定性,LA 为实现经济收益最大化,都会尽可能在电价高峰时段安排削减负荷和储能放电,在低谷电价时段安排转移负荷和储能充电,这也满足了电网削峰填谷的要求。同时,用户在自己可以接受的削负荷范围内能够根据合同获得来自LA 的奖励。据此也验证了电网、LA、用户三者的互利共赢关系以及LA 模式的可行性。

3.2 预测数据与场景

本文选取某地75 日电网工作日负荷数据,负荷数据的时间间隔为15 min,即24 h 含有96 点负荷数据。依据0.8∶0.2 的比例划分训练集和测试集,得到60 个工作日的训练集和15 个工作日的测试集,并在附录D 图D4 中展现出一周的历史负荷数据。

考虑到负荷数值的变化相对于基量的变化不够明显,因此需要利用min-max 归一化处理以凸显负荷的变化趋势。同时,将数据归一化到［0,1］之间也有利于神经网络的训练,得到更准确的预测值。

为便于分析DR 信号和用户参与DR 不确定性这2 种因素对LSTM 超短期负荷预测模型的影响,需设置预测场景进行对比。同时,根据上文方法及流程图可知,若不计及LA 模式下的DR 信号,即在负荷预测中忽略DR 的作用,则不存在关于是否计及用户参与DR 不确定性的讨论。因此,本算例设定3 种预测场景如下:

场景1:不计及LA 的DR 信号,不考虑用户参与DR 的不确定性,预测下一个15 min 时段的负荷。

场景2:计及LA 的DR 信号,但不考虑用户参与DR 的不确定性,预测下一个15 min 时段的负荷。

场景3:计及LA 的DR 信号,并考虑用户参与DR 的不确定性,预测下一个15 min 时段的负荷。

在计算各场景预测结果时,为得到最优超参数,首先依照经验试验部分超参数,得到了最优超参数的大致范围；然后依据网格搜索法,搜寻得到适用于4 种场景的最优超参数均为:网络层数为5 层、学习率为0.01、批处理数为32。

3.3 预测结果及场景分析

根据上述算例,求得3 个场景负荷预测值与真实值,并进行对比。图4 展现了测试集中某一周的周一预测分析曲线,在附录D 图D5 中展示该周其余工作日的负荷预测结果。同时,为更清晰地凸显各场景差异,考虑到用户用电在峰时段和谷时段受DR 信号的影响较大,因此选取部分峰时段和谷时段的预测结果,如附录D 图D6 和图D7 所示。

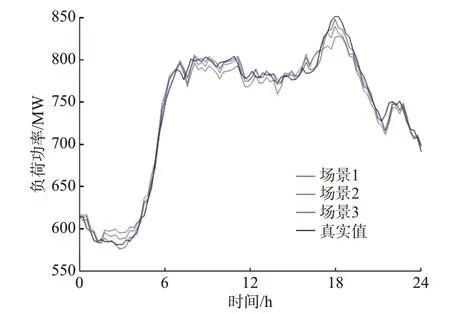
图4 各场景负荷预测结果与真实值Fig.4 Load forecasting result and real value of each scenario

将图4 各预测结果与真实值的对比作定性分析,3.1 节得到的DR 信号对LSTM 模型产生了一定影响,主要体现在峰时段和谷时段能够更好地模拟用户行为,反映负荷变化趋势,使得超短期负荷预测效果更佳,更接近真实值。同时,在考虑用户参与DR 不确定性后,即场景3,能够进一步减小与真实值曲线的误差。

为定量分析3 种场景下的预测误差情况,计算一日内各时段的相对百分比误差,如图5 所示。

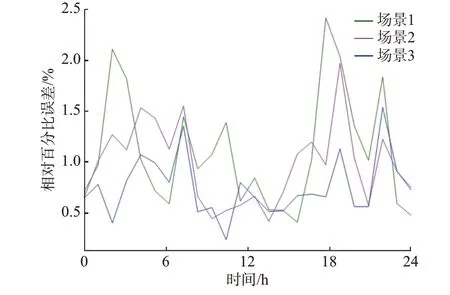
图5 各场景一日内的相对百分比误差Fig.5 Relative percentage error of each scenario in one day

可以发现,从场景1、场景2 到场景3,相对百分比误差整体上逐渐减小,尤其是在峰时段及谷时段误差减小得更加明显。同时,场景1 所有时段的误差波动范围为0.36%～2.40%,场景2 所有时段的误差波动范围为0.38%～1.85%,场景3 所有时段的误差波动范围为0.17%～1.48%,波动范围逐渐减小。

进一步,为验证本文所提计及LA 模式下DR 信号的超短期负荷预测方法的泛化能力,选取测试集中5 个工作日,按上文所述方法进行误差分析,计算得到周一至周五及整个测试集在3 种场景负荷预测RMSE 值和MAPE 值,如 表1 所示。

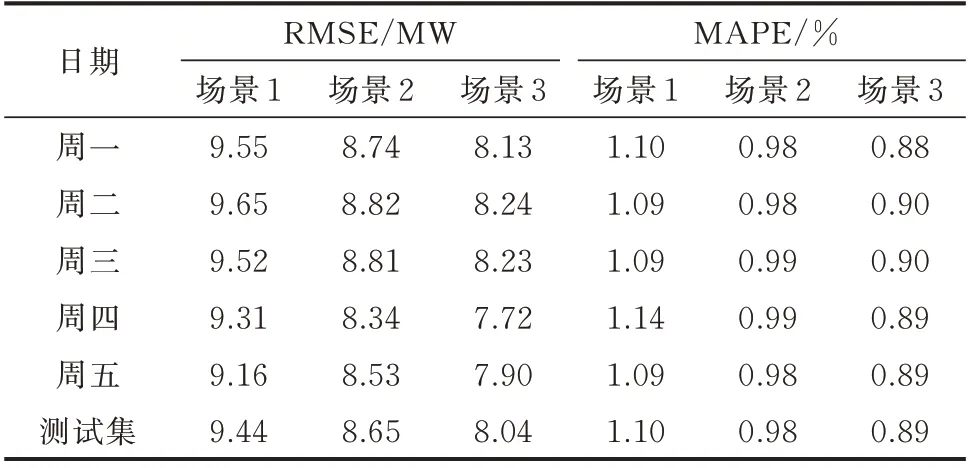
表1 测试集预测误差对比Table 1 Comparison of prediction error of test sets

可以发现,一周内工作日的情况略有差别,但从场景1 到场景2 再 到场景3 的RMSE 值和MAPE 值均逐渐减小,预测效果逐渐变好。为了反映一周内的整体变化情况,需要分析整个测试集的RMSE 值和MAPE 值。相较场景1,场景2 在计及LA 模式下DR 信号后,获取了DR 的信息,反映用户用电行为,负荷预测曲线能够更接近真实值曲线,RMSE 值减小0.79 MW,MAPE 值减小0.12%,提高了10.91%的精度。相较场景2,场景3 在计及LA 模式下DR信号的基础上,进一步考虑用户参与DR 的不确定性,更接近用户行为的实际情况,提高了DR 信号的准确度,使得负荷预测曲线更加接近真实值曲线,RMSE 值减小0.61 MW,MAPE 误差减小0.09%,进一步提高了8.18%的精度。

总的来说,虽然计及DR 信号的负荷预测模型增加了输入量的维度,使模型在LSTM 结构和训练上更复杂,但在LA 模式下,负荷预测时考虑DR 信号以及用户参与DR 的不确定性因素能够更好地预测负荷的变化趋势,减小预测误差。

4 结语

本文提出了基于LA 模式下DR 信号的LSTM超短期负荷预测方法,主要研究成果如下:

1）分析了LA 模式的DR 机制,建立了IL、TL、光储单元和HL 这4 种DR 资源的优化模型。

2）考虑用户参与DR 的不确定性,基于消费者心理学,通过三角隶属度函数描述的模糊参数反映用户参与DR 实际项目的不确定性。

3）在预测方法方面,在传统LSTM 负荷预测模型的基础上进一步考虑LA 模式下DR 的影响,建立了计及DR 信号的LSTM 负荷预测模型。

4）以实施LA 的某地区历史负荷作为算例分析,对比3 种预测场景验证了本文所提方法的优势,计及DR 信号并考虑DR 不确定性后能够更好地反映用户行为,误差更小,峰时段和谷时段尤为明显。

5）对比3 种场景下的平均值,计及DR 信号后预测精度提高10.91%,在此基础上考虑用户参与DR的不确定性后,预测精度进一步提高了8.18%,RMSE 值减小到8.04 MW,MAPE 值减小到0.89%,满足误差要求,也验证了所提方法的泛化能力。

本文研究在LA 模式下考虑DR 信号的超短期负荷预测,具有一定的工程实用价值,在LA 规划、调度、制定电价等方面起到了基础性作用。下一步的研究将探讨引入用户决策行为的DR 信号形成方法,以及进一步研究LA 模式的电价预测和负荷弹性预测。

本文受到广东电网有限责任公司广州供电局科技项目(GZHKJXM20180152)资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。