基于频繁模式挖掘的风电爬坡事件统计特性建模及预测

屈尹鹏，徐 箭，姜尚光，柳 玉，孙元章，柯德平

（1. 武汉大学电气与自动化学院,湖北省武汉市430072；2. 国家电网公司华北分部,北京市100053）

0 引言

风电等高比例可再生能源发电的接入［1］,对电力系统的辅助服务［2-3］提出了更高的要求。准确建立可再生能源爬坡事件的统计特性和预测模型,能更好地为辅助服务提供数据支撑［4-7］。

文献［8］采用旋转门算法分析了爬坡事件单属性统计特性。文献［9-10］采用L1 滑窗算法和动态规划算法进行爬坡检测,并建立了爬坡参数的二维统计特性模型。文献［11］分析了不同季节下爬坡参数统计特性的差异。文献［12］分析了风电原始数据特性对检测到的爬坡事件单个参数统计特性的影响。文献［13］将风电功率映射到频域空间,建立了爬坡事件各个参数的时频特性并进行分类。文献［14］采用高斯混合模型拟合爬坡参数的一维概率分布。

风电爬坡预测可分为间接功率序列预测［15-16］和事件预测［17-18］两大类。文献［19］采用优化的旋转门算法从大量风电功率预测场景中提取风电爬坡事件。文献［20］使用风电功率序列多项式logit 结构和分类分布估计爬坡事件超出不同参数阈值的概率。文献［21］利用风电功率的分位数生成功率场景,通过逻辑回归来估计在特定时间间隔内风电爬坡发生的概率。文献［22］建立了正交检验和支持向量机的混合预测模型,分析当前点发生爬坡事件的概率。文献［23］使用Granger 因果检测法,构建了基于多变量的支持向量机回归预测模型,对下一次爬坡事件进行预测。文献［24］对风电功率爬坡持续时间和爬坡幅值采用原子分解算法进行滑动分解得到原子分量和残差分量进行预测,并采用线性回归方法校正各个参数的误差。

爬坡统计特性建模的基本现状是:①对单个爬坡事件而言,多为单属性或双属性的统计特性建模分析；②相邻爬坡事件之间自相关统计特性模型研究较少。针对上述问题,本文提出了爬坡事件的多属性联合统计特性建模方法。基于该模型得到爬坡事件的基本模式,将风电功率序列降维为爬坡事件序列,对其进行频繁项挖掘从而进一步建立多个相邻爬坡事件之间的自相关统计特性模型。

现阶段爬坡预测尚待解决的主要问题体现在:①基于事件的预测方法无法全方位充分利用爬坡事件的历史信息；②日前爬坡预测往往通过对日前的风电功率预测数据进行爬坡检测得到。但由于预测的点数较多、易造成爬坡预测误差的累积和发散,从而造成爬坡事件的正确捕获率的降低。针对上述问题,本文基于所提出的爬坡事件基本模式以及爬坡事件的自相关统计特性模型,设计了一种日前爬坡事件序列预测算法。以爬坡事件为预测点,通过自相关模型进行迭代,生成新的预测事件。相较于以风电功率为预测点的间接爬坡事件预测算法,其有效地减少了爬坡事件预测中的误捕和漏捕现象。

1 爬坡事件多属性统计特性建模

1.1 参数和分辨率自适应算法的爬坡事件检测

文献［12］提出了一种对参数和数据分辨率进行鲁棒分析的爬坡检测算法——参数和分辨率自适应算法（PRAA）,其使用异常旋转门算法［25］对原始数据进行坏数据处理和趋势拟合,旋转门的检测公式为:

式中:Vc为当前被检测点的信号幅值；Vo为起点的信号幅值；Vg为门点的信号幅值；tc为当前时刻；tg为门点的时刻；to为起始点的时刻；Vub为上边界；Vlb为下边界；ε 为旋转门的门宽。

得到的旋转门数据段代表了原始数据的趋势,可以用来进行爬坡检测。该爬坡检测共分为如下2 个阶段。

第1 阶段用来合并相邻的具有相同方向的旋转门数据段。 给定一个风电旋转门序列X ={(t1,p1),(t2,p2),…,(tm,pm),…,(tN,pN)},其 中,tm为时标,pm为该时标下的风电功率,N 为风电旋转门数据段总数。 风电爬坡事件集合表示为EX={ E1,E2,…,Ed,…,EL},其中,Ed={ sd,ed},sd为第d 个爬坡事件的起点,ed为第d 个爬坡事件的终点,L 为该集合中总的爬坡事件数,则合并标准可写为:

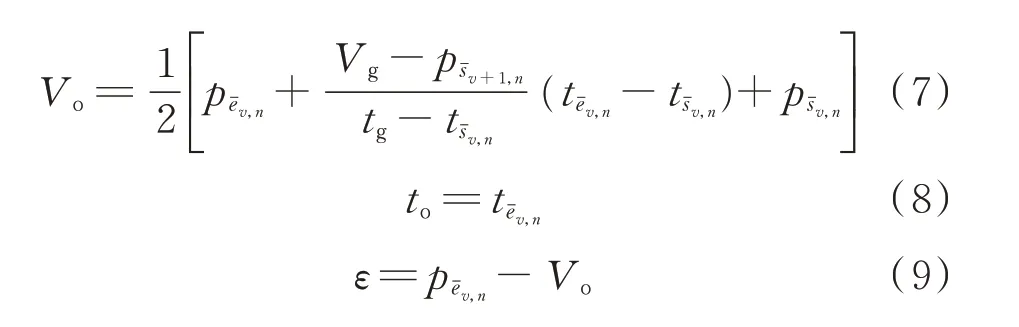
将式（5）—式（9）求出的等效旋转门参数代入式（1）中进行检测,若式（1）成立,则这2 个非有效爬坡事件属于同一趋势段,进行合并；否则属于不同的趋势段,继续检测下一对非有效爬坡事件。有关于PRAA 的详细信息参见文献［10］。

在本文中,有效爬坡事件的定义为:

式中:PGN为风电场的额定功率。

式（10）和式（11）表示,如果风电功率4 h 内向上爬坡20% 的额定功率或向下爬坡15% 的额定功率,则判定为发生一次有效爬坡事件。通过PRAA得到的所有有效爬坡事件集合和爬坡间隔将作为下一阶段爬坡分类的输入数据。

1.2 联合统计特性检测

爬坡事件具有3 个重要属性:爬坡幅值、爬坡斜率和爬坡持续时间。通过对原始风电数据进行爬坡检测,可以得到爬坡事件单个属性的统计特性。在此基础上,对爬坡事件集合进行多属性聚类得到爬坡事件的多属性统计特性模型。为了方便对风电功率时间序列进行事件重编码,本文选择爬坡起点、爬坡持续时间和爬坡终点作为爬坡事件的数据属性。需要注意的是,这3 个属性同样包含了幅值和斜率信息。通过实验发现,爬坡事件的联合分布图具有分布区域形状复杂、分布密度具有伸缩性和延展性等特点。以中国某风电场一年实测数据中的向上爬坡事件为例,爬坡事件多属性联合分布图如附录A图A1 所示。

附录A 图A1（a）中,红色圆圈部分为高密度区域,绿色圆圈部分为中密度区域,剩余部分为低密度区域；图A1（b）中,红色三角形部分为高密度区域,绿色三角形部分为中密度区域,剩余部分为低密度区域。由于在一个聚类过程中需要不同的密度参数,而常见的密度算法［26］对输入的参数极为敏感,因此不适用。又由于簇形状的复杂性,使得圆形簇聚类算法如K-means 算法［27］也不适用。

针对上述难点,本文使用排序识别聚类结构（ordering points to identify clustering structure,OPTICS）算法［26］进行数据挖掘,通过输出点的距离排序的方式聚类,因此能够检测到任意形状的簇,并保持对输入参数的鲁棒性,适用于风电爬坡事件多属性联合统计特性检测。OPTICS 算法的基本参数及原理见附录A。

在进行聚类之前为了保证点距离不会被某一个数据属性所淹没,需要对所有数据点的属性值进行标准化,即转化到一个特定的数据区间内,如[-1,1]。为了防止噪声点对标准化的影响,本文使用中位数和绝对标准差进行数据x 的标准化,即

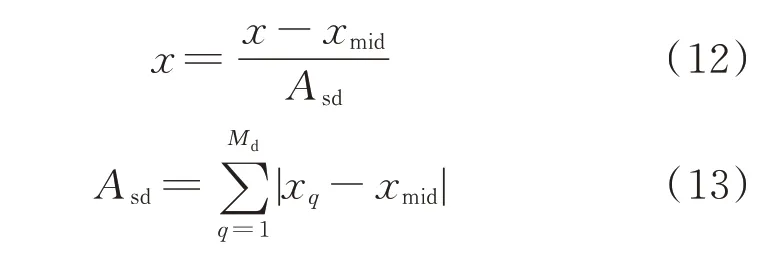
式中:Asd为绝对标准差；xmid为中位数；Md为对象的个数；xq为第q 个对象。

OPTICS 算法流程见附录A 图A3。不断更新有序队列（核心点及该核心点的直接密度可达点）和结果队列（存储样本输出及处理次序）,直至数据库为空。最后,OPTICS 算法输出的结果队列保证了距离近的点在一起,可根据簇排序决定最后实际的输出聚类,从而检测出爬坡事件的基本模式即多属性联合统计特性。

2 基于关联规则算法的爬坡事件自相关性建模及预测

2.1 时序序列的事件编码

基于功率时序序列的日前爬坡预测易造成误捕和漏捕的很大一部分原因是预测的点数较多,误差的累积和发散难以控制。因此,如何从功率序列中提取出有效信息和摒弃冗余信息来进行时序序列降维,对减少爬坡预测的预测点和提高事件捕获率显得尤为关键。

通过爬坡事件聚类所用的数据属性（爬坡起点、爬坡终点、爬坡持续时间和爬坡间隔持续时间）能够完整地表达时序序列中的爬坡信息。再者,使用爬坡事件和爬坡间隔进行聚类得到的爬坡模式完成对时序序列的重新编码,如图1 所示。时序序列{(t42,p42),(t43,p43)…,(t190,p190)}能够重编码为事件序列{A,B,C},其中,A,B,C 为爬坡事件聚类得到的爬坡模式（簇）。以模式A 数据段为例,数据段内的小幅波动信息对于爬坡事件来说为冗余信息,而红色直线为爬坡事件,包含有效的爬坡信息（爬坡幅值、爬坡持续时间、爬坡起点、爬坡斜率等）。由于模式A 为爬坡聚类得到的基本模式（簇心）,因此,若使用模式A 来代表该爬坡事件,会损失一定程度的爬坡信息,然而由于模式A 为聚类的簇心,因此损失的信息是有限的。同样对模式B 和模式C 的数据段进行降维编码之后,可将一个150 维的功率序列降维为一个3 维的事件序列。

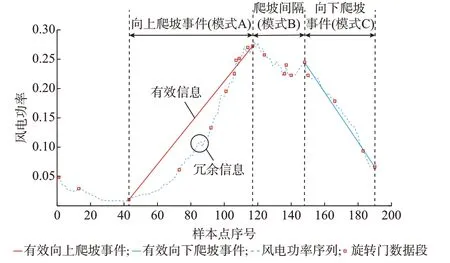
图1 事件编码图Fig.1 Diagram of event encoding

2.2 关联规则算法的关联性分析

在风电功率预测中,风电功率的自相关特性往往被用来进行功率序列的预测。然而在爬坡预测模型中,由于缺少类似的风电爬坡事件的自相关统计特性模型,现阶段基于事件的爬坡预测大部分集中于中短期的爬坡预测,因此在进行了功率序列的事件重编码之后,进一步挖掘出爬坡事件的自相关特性,有助于爬坡事件序列预测模型的建模。

本文采用关联规则挖掘算法——APRIORI 算法进行爬坡事件频繁模式挖掘,建立爬坡事件的自相关统计特性模型。APRIORI 算法［26］的基本参数及原理见附录B。

本文应用上述方法对2.1 节中的模式事件序列进行搜索。由于相隔较远的爬坡事件相关性较小,只需考虑到频繁四项集即可,即依次包含2 起爬坡事件和2 个爬坡间隔的频繁项集。因此,从频繁二项集到频繁四项集包含了爬坡事件的自相关信息。例如,附录B 图B1 中,在模式A 发生之后,模式B 发生的概率如式（14）所示,其中（A,B）、（A,E）、（A,F）为所有包含模式A 的频繁二项集,从而建立起模式A 和模式B 的自相关特性。

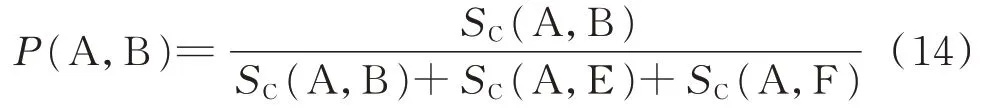
式中:SC(⋅)为支持度计数函数；E 和F 为爬坡模式。

2.3 基于事件序列的爬坡预测模型

为了展示爬坡事件的联合属性统计特性和自相关统计特性对于风电爬坡预测的数据支撑作用,本文研究了一种基于上述统计特性模型的爬坡事件序列预测的基本概念和模型。

本文采用功率事件对的形式交替进行预测。给定一个功率点事件对Fd={(td,pd),Rd},td为第d 个爬坡事件起点时刻,pd为第d 个爬坡事件起点的功率值,Rd=(Ud,Gd)为第d 个爬坡事件,其中,Ud为持续时间,Gd为爬坡幅值,若为爬坡间隔模式,则爬坡幅值为0。给定预测起始点前3 个爬坡模式为{MO1,MO2,MO3},频繁二项集至频繁四项集的支持度计数分别为SC2(⋅),SC3(⋅),SC4(⋅),括号内为相应的模式。将首个功率事件对的功率点设置为第3 个爬坡模式的终点,则首个爬坡事件的预测模型为:

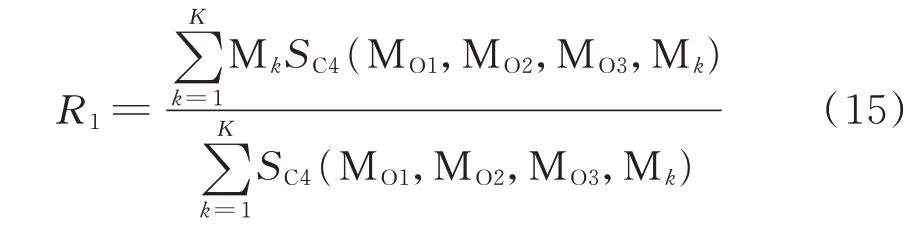
其中,K 为频繁四项集中前 3 项为{MO1,MO2,MO3}的频繁项的总个数,Mk为其中第k 个频繁项的第4 个模式。需要注意的是,若K 为0,删除MO1,在频繁三项集中进行匹配,若仍然没有匹配到相应的频繁项,则在频繁二项集中进行搜索。直至得到首个功率事件对F1={(t1,p1),R1},接着进行第2 个功率事件对功率点的预测,其预测模型为:

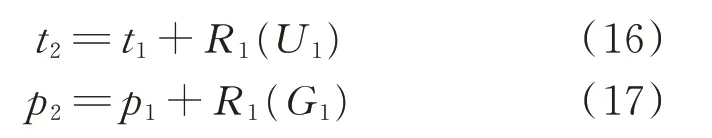
提取第1 个爬坡事件的起点、爬坡终点和爬坡持续时间,计算其与已有各个模式簇心的距离,将其归为距离其簇心最近的模式,设为MOn,然后更新前3 个爬坡模式为:

在更新完已有模式之后,用式（15）进行第2 个爬坡事件的预测,用式（16）和式（17）进行第3 个功率事件对功率点的预测,重复该过程,交替预测功率事件对的功率点和爬坡事件并更新,直至完成一天的爬坡事件预测。式（15）—式（18）为爬坡事件序列预测模型,其流程图见附录C 图C1。

从预测模型中可以发现,正是由于爬坡事件自相关模型的建立,才能够通过式（15）由历史爬坡事件序列推导出新的爬坡事件序列。且由于对功率序列进行了降维,减弱了预测误差累积及发散,从而提高了爬坡事件的捕获率。

整体算法的结构图见附录C 图C2。爬坡检测为所有算法的基础,本文所使用的PRAA 能够对不同数据源和数据属性（如分辨率）的数据库进行原始数据处理和爬坡检测,得到的有效爬坡事件集合作为其他算法的输入数据。对PRAA 得到的爬坡事件集合使用OPTICS 算法进行爬坡聚类,可以得到爬坡事件的多属性统计特性建模,即基本爬坡事件模式。基于OPTICS 算法得到的基本爬坡模式,对风电功率序列进行事件重编码,使用关联规则算法对事件序列进行频繁模式挖掘,即可以得到爬坡事件的自相关统计特性模型。所得到的单爬坡事件多属性统计特性模型和爬坡事件自相关统计特性模型为辅助服务或爬坡预测等高级应用提供数据支撑。

3 算例分析

本文通过2 个实际风电场的原始数据集来验证所提算法的有效性。第1 个数据集来自BPA（Bonneville Power Authority）,包含2 年共184 032 个数据样本,采样时间间隔为200 s。该数据集主要用来展示所提的爬坡聚类方法并验证其有效性。第2个数据集来自中国中部省份某风电场,共包含1 年6 个月的风电功率数据,采样时间间隔为15 min,有58 477 个实测点和58 477 个预测点（来自某商用预测软件）。该数据集主要用来验证所提爬坡事件自相关统计特性建模方法并对比展示基于事件序列的爬坡预测效果。其中,1 年5 个月的数据用来做样本学习集,剩余1 个月的数据用来验证预测算法。

3.1 数据集1 算例

对BPA 的原始风电数据进行PRAA 爬坡检测,共检测到1 062 次有效爬坡事件,其中包括478 次上爬坡事件和584 次下爬坡事件。检测到的上爬坡事件的二维属性分布见附录D 图D1。从图D1 中可以发现,小幅值、短时间的爬坡事件密度较高,而爬坡起点和终点的分布则相对而言较为均匀,呈现倒三角的形式。上爬坡事件的三维属性（爬坡起点、爬坡终点和爬坡持续时间）的整体分布图以及使用OPTICS 进行聚类得到的结果如图2 所示。BPA 的上爬坡事件分类如表1 所示。

图2 上爬坡事件聚类图Fig.2 Cluster diagram of up-ramp events

表1 BPA 的上爬坡事件分类Table 1 Classification of up-ramp for BPA

对上爬坡事件聚类得到3 种模式,如表1 和图2所示。其中,模式1 和模式2 均代表小幅值且短时间的爬坡事件,区别在于模式1 的爬坡起点较低而模式2 则表征高起点的爬坡事件,小幅值且短时间的上爬坡事件占所有上爬坡事件的86.4%。模式3代表大幅值、长持续时间且低起点的上爬坡事件,其占比为13.6%。

检测到的下爬坡事件的二维属性分布见附录D图D2,其整体分布特性与上爬坡事件分布特性类似。对下爬坡事件聚类得到4 种模式,见表D1 和图D3。其中,模式5 代表小幅值、超短持续时间且高起点的爬坡事件,占比为35.96%；模式6 代表小幅值、短持续时间且低起点的爬坡事件,占比为40.07%；模式7 代表大幅值、超长持续时间且低起点的爬坡事件,占比为12.67%；模式8 代表大幅值、长持续时间且高起点的爬坡事件,占比为11.99%。

爬坡间隔由持续时间构成,对其进行聚类,可得到6 种模式,见附录D 表D2。可以发现,短期的爬坡间隔占比较高。如4 h 内的爬坡间隔占比为73.43%。而长时间的爬坡间隔如9 h 以上的则占比较少,为26.57%。需要特别注意的是模式12,其爬坡间隔时长为0,说明发生了连续爬坡事件,如发生了上爬坡事件之后立刻发生下爬坡事件,该类事件所造成的爬坡间隔为0 的占比为22.6%。若该类爬坡间隔的占比较高,说明该地区的风电波动相当频繁,否则说明该地区的风电相对平稳。因此,爬坡间隔为0 占整体爬坡间隔的比例能够作为一个地区风电波动特性的体现。

至此,数据集1 的爬坡事件多属性联合统计特性检测完成。在单属性的统计特性的基础上,多属性统计特性模型进一步完善了爬坡事件统计特性建模,使得对于爬坡事件的描述更加直观和完整,对风电爬坡预测能够给予更好的数据支撑。

3.2 数据集2 算例

对数据集2 的实测数据学习集进行爬坡检测并进行事件聚类,得到5 个上爬坡模式、5 个下爬坡模式和6 个爬坡间隔模式。如前所述,数据集2 主要用来验证爬坡事件自相关统计特性模型,由于篇幅限制,其聚类结果不在此展示。

为便于事件编码,将上爬坡模式编号为1～5,下爬坡模式编号为6～10,爬坡间隔模式编号为11～16。对重编码之后的事件序列进行APRIORI算法关联性分析,设定频繁项阈值为10 个支持度计数。

如附录D 图D4 所示,共搜索到91 个频繁二项、126 个频繁三项和33 个频繁四项。其中,频繁二项集总的支持度计数和为4 534,频繁三项集的支持度计数和为2 587,频繁四项集的支持度计数和为537。图3 和附录D 图D5 分别为频繁四项集和频繁三项集具有相同N -1 前缀项的示例。

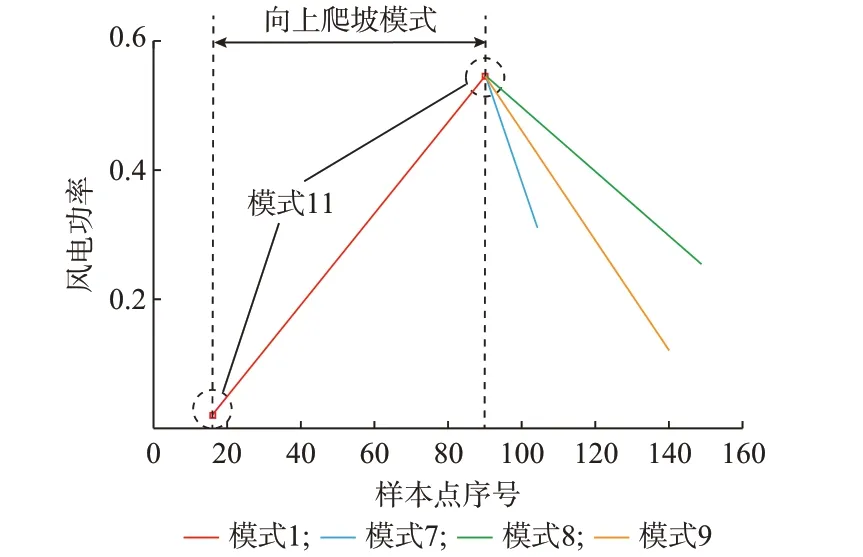
图3 频繁四项集自相关特性示例Fig.3 An example of autocorrelation characteristicin frequent four itemset

图3 显示前缀为11,1,11 的频繁四项第4 项的概率图。其中,模式11 为爬坡间隔模式,持续时间为0,模式1 为上爬坡模式。从图中可以看出,当前面接连发生爬坡事件（间隔）的模式分别为11,1,11后,紧接着会发生一起下爬坡事件（模式7,8,9 均代表下爬坡事件）且模式8 下爬坡事件概率最大,为49%。模式7 和9 下爬坡事件的发生概率相近,分别为24%和27%。这样就建立了模式11,1,11 和模式7,8,9 的自相关特性统计特性模型。但由于频繁四项集内项数较少,在某些情况下可能匹配不到相同的前缀,此时需从频繁三项集中进行搜索。

如附录D 图D5 所示,当发生了模式9 和11 的爬坡事件和爬坡间隔之后,接下来会发生一起上爬坡事件（模式1,2,3,4 均代表上爬坡事件）,其中模式2和3 上爬坡事件的概率较大,分别为35%和33%,而发生模式1 和4 上爬坡事件的概率较小,分别为14%和17%。这样就建立了模式9,11 和模式1,2,3,4 的自相关统计特性模型。同样,若在频繁三项集中匹配不到前缀,则继续搜索频繁二项集。因此,频繁二项集、频繁三项集和频繁四项集表征了爬坡事件的自相关特性。

为了展示这种基于事件序列自相关特性的风电爬坡事件预测方法的效果,本文将其所得到的结果与基于风电场风电功率预测序列的爬坡检测结果进行对比。

如附录D 图D6 所示,一个月的实际风电功率数据中共检测到150 起有效风电爬坡事件,而风电功率预测数据中仅检测到39 起爬坡事件,并且出现多次误捕的现象。该预测软件预测周期为24 h,预测数据分辨率为15 min,即一天产生96 个预测点。漏捕的主要原因是爬坡误差在96 点预测过程中的不断积累和发散。然而,本文所提的基于事件序列自相关特性的风电爬坡事件预测能够预测到168 起爬坡事件,其中,误捕27 次、漏捕9 次。图4 展示了该月第一天的预测效果。日前捕获率相较于基于功率序列的爬坡预测有了提高。这也体现了本文所研究的爬坡事件多属性统计特性模型和爬坡事件自相关统计特性模型对于日前爬坡预测所提供的数据支撑的有效性。

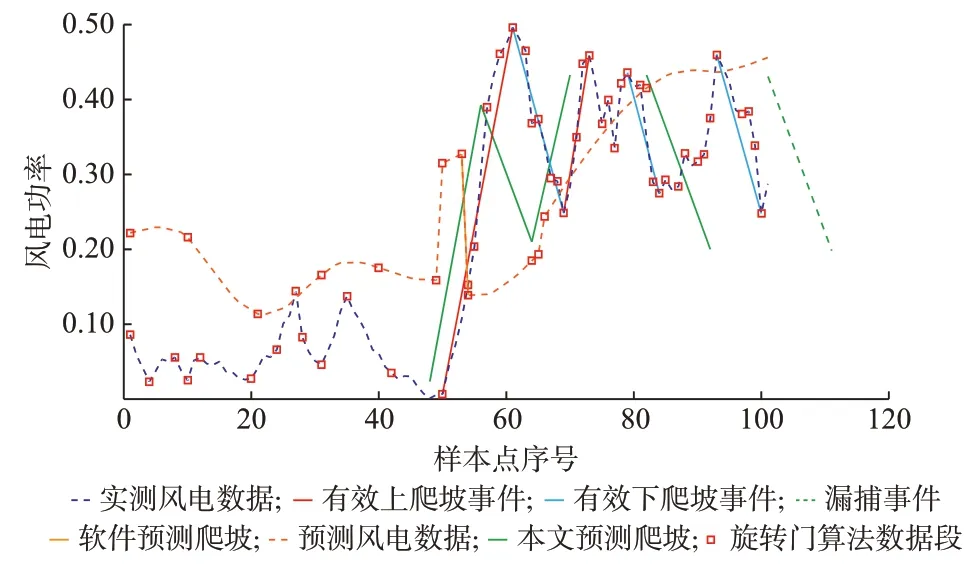
图4 一天预测效果对比Fig.4 Comparision of forecasting results in one day

从图4 中可以发现,虽然风电功率预测序列能够大致在趋势上拟合实际的风电功率序列,但由于其预测误差会随时间发散,无法起到爬坡预测的作用。相反的,若使用基于事件序列自相关特性的爬坡预测方法,虽然无法提供逐点的风电功率序列信息,但却能够在爬坡事件上做到相当高的捕获率。从算例结果中发现,漏捕9 次的主要原因如图4 绿色虚线所示,由于爬坡起点的预测误差累积,导致一天之内最后一起预测爬坡事件起点距离预测起点超过24 h,因此没有计入当日的预测事件中,从而出现漏捕事件。从上述算例中可以发现,仅依靠风电功率进行爬坡预测的精确性仍然有提高的空间。

4 结语

本文利用数据挖掘技术、设计了一套爬坡事件统计特性建模方法,主要包含以下几个步骤:①PRAA 的原始风电数据爬坡检测,得到历史风电爬坡数据集；②OPTICS 算法爬坡聚类,得到单爬坡事件多属性统计特性模型；③关联规则算法频繁模式挖掘,得到爬坡事件自相关统计特性模型。通过BPA 风电场数据和国内某风电场数据的对比验证可以发现,所提算法的多属性联合统计特性模型相较于单属性或双属性统计特性模型能够更为完整且直观地提供爬坡事件信息。所提出的爬坡事件自相关统计特性模型在以往仅提供单个爬坡事件的统计特性模型的基础上,能够进一步提供相邻爬坡事件的相关特性。

在此基础上,本文研究了基于上述模型的日前爬坡事件序列预测的基本概念和模型。实验证明,相较于某商业软件的基于风电功率序列的间接爬坡预测算法,本文所研究的方法在不包含误差控制算法的前提下,能够提供更高的爬坡事件捕获率,将漏捕事件从功率事件序列预测算法中的111 次减少到了9 次,反映了本文所研究的爬坡事件统计特性模型对于爬坡预测算法的数据支撑作用。

本文所提预测模型仅包含了风电功率数据,在未来工作中,将通过引入数值天气预报数据来抑制爬坡事件预测误差的累积和发散,进一步提升爬坡事件预测算法的正确捕获率,合理选择预测时间窗,建立中长期的爬坡事件序列预测模型。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。