Bootstrap法与H-L法中位数差值区间检验在非劣效试验中的模拟比较研究*
成都医学院公共卫生学院(610500) 毛 昂 曾子倩 魏 敏 陈晓芳 陈卫中
【提 要】 目的 比较Bootstrap法和Hodges-Lehmann法(H-L法)在中位数差值非劣效性检验中的特点,为相关研究中统计学方法的选择提供依据。方法 以某临床试验中试验组与对照组咽痛消失时间的比较为基础,通过计算机模拟生成单组样本量分别为20、30、50、100、200各500个两独立样本,分别服从参数为90h(试验组)、100 h(对照组)的Poisson分布。针对每个样本采用基于正态近似和百分位数的Bootstrap法、H-L法求得中位数差值的置信区间,并通过置信区间下限与非劣性界值进行比较,得出三种方法的检验效能。结果 三种方法均随着样本量增加,检验效能增加。在样本量为20时,H-L法与正态近似法检验效能相当(25% vs.24%),且都高于百分位数法(19%)。在样本量为30、50、100时,H-L法检验效能高于正态近似法与百分位数法,且正态近似法高于百分位数法。在样本量为200时,三种方法的检验效能相当,均在95%以上。结论 整体来看,H-L法获得的区间最窄且最稳定,检验效能最高,尤其在样本量不大时建议选择H-L法。
非劣效性试验(non-inferiority trials)被广泛应用于药物临床试验研究。有关非劣效性检验的方法主要有假设检验法和区间检验法两种[1]。目前针对定量资料均数非劣效性检验的方法较为成熟,如t检验法、均数差的置信区间法,以及基于模型边缘均数置信区间法等[5]。但越来越多的临床试验中以某一临床事件发生或达到预先规定标准的时间分布情况作为药物的疗效指标[2],其观察结果多呈偏态分布,且存在不确切值为开口资料,采用中位时间作为疗效描述和比较指标更为恰当[3-4]。针对中位数的非劣效性区间检验的主要有H-L法和Bootstrap法两种,关于两种方法在非劣效试验中的检验效能比较报道较少。因此,本文以评价某医药公司生产的七味清咽气雾剂咽痛缓解时间为例,比较上述两种区间检验方法在不同样本量下的检验效能,为相关研究中统计学方法的选择提供依据。
对象与方法
1.对象
为评价某公司生产的七味清咽气雾剂的有效性,以标准药物作为对照,共纳入280名受试对象,随机等分为试验组和对照组。以疼痛消失时间为有效性评价指标,在6天的临床用药观察中,对于咽痛未消失患者的疼痛消失时间记为“>144h”,为典型的开口资料。试验结果显示对照组的咽痛消失时间的中位数为90h,试验药物组疼痛消失时间中位数为100h,非劣效性临界值Δ设定为15h,即中位数差值>-15可做出试验药物非劣于标准药物的结论。
2.方法
(1)数据分布及参数的选择
本研究中,假定数据服从Poisson分布,即试验组和对照组的结局变量X1、X2分别服从参数为1和2的Poisson分布,结合试验结果记为X1~P(90),X2~P(100)。
(2)样本量的确定
根据经验,结合临床实际,模拟研究中单组样本量分别设定为20、30、50、100和200,以考察不同样本量下检验方法的表现与检验效能。
(3)Hodges-Lehmann法

(1)

(U(Cα),U[(n1×n2)+1-Cα])
(2)
其中Cα是一个小于等于置信区间下限的最大整数,表达为:
(3)
(4)Bootstrap可信区间法
Bootstrap方法最早由美国斯坦福大学统计学教授Efron[9]在1979年提出的。本研究中,在每种样本含量下通过数学模拟产生500个Poisson分布样本,并对每个样本进行有放回、且样本量不变的重复抽样,获得500个Bootstrap样本,计算得到其中位数差值的置信区间。其具体步骤为:
①计算Poisson分布样本数据的中位数M1、M2及M1-M2;
②对两样本分别进行有放回样本例数固定的Bootstrap抽样,获得用于计算标准差的Bootstrap样本;
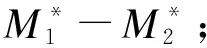
④重复②-③步骤500次,获得500个Bootstrap样本及500个中位数之差;
⑤置信区间计算方法:
L(M1-M2)B=(M1-M2)-ZαSE(M1-M2)B
(4)
b.Bootstrap百分位数法:用500个Bootstrap样本获得的500个中位数之差,并将中位数之差P2.5作为中位数之差的置信区间下限。
(5)检验结论及检验效能估计

(6)软件实现过程
通过SAS 9.4进行数据模拟,并完成两种中位数差值的置信区间检验方法在非劣效性试验中的比较。非劣效性检验中检验水准α设定为0.025。
结 果
1.H-L法、正态近似法和百分位数法95%置信区间的比较
H-L法的95%置信区间明显比正态近似法波动范围小,置信区间的宽度也要小于正态近似法,且每种方法的置信区间都包含中位数真实差异10h。同时,各组样本量上H-L法置信下限的标准差均小于Bootstrap正态近似法和百分位数法。具体见表1和图1。

表1 H-L法、正态近似法和百分位数法中位数差值95%置信下限的比较
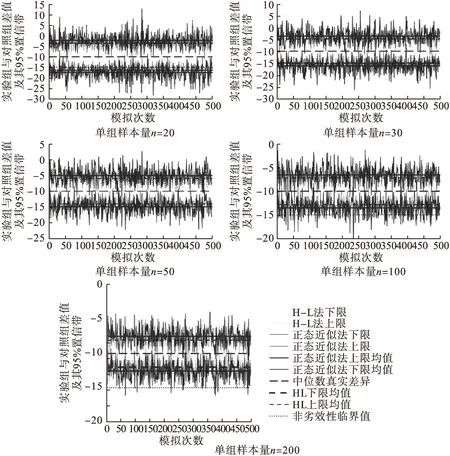
图1 正态近似法和H-L法95%置信区间比较
2.三种方法的检验效能比较
三种方法的检验效能都随着样本增加而增加。在n=20时正态近似法和H-L法相当,但随着样本量的增大,H-L法均好于正态近似法和百分位数法。且在n≥100时,H-L法明显好于正态近似法和百分位数法,而正态近似法和百分位数法相差不大。具体见表2和图2。

表2 三种方法检验效能的比较[n(%)]
3.两组受试者咽痛消失时间的比较
两组受试者咽痛消失时间的比较中,三种检验方法的置信下限均大于非劣效性界值,均得出试验药非劣于对照药的结论。但H-L法的置信区间最窄。具体见表3。

表3 两组受试者咽痛消失时间差值及其95%可信区间(h)
讨 论
本研究探讨了两种中位数差值的区间检验方法在非劣效试验中的模拟比较研究。在样本量为20时,正态近似法的检验效能和H-L法的检验效能相差不大。但随着样本量的增大H-L法的检验效能先是明显高于正态近似法,在样本量到200时,两种方法的检验效能趋于一致。不论样本量是多少,正态近似法的置信区间波动范围都大于H-L法,且不如H-L法稳定,其原因可能和两种方法利用样本信息程度有关。H-L法充分利用每一个样本信息,每一个观测都要与另一组的每个观测进行相减,且在后续计算中所占权重相等,并对极端值有较为稳健的处理[10]。而正态近似法则较多的考虑了原始样本中位数的差异,其次,Bootstrap法还与原始样本量有关,本研究中在单组样本量为200时,正态近似法得到的置信区间波动范围较样本量为100时有了明显改善,应注意的是在应用Bootstrap法估计中位数置信区间时是基于样本很好地代表总体的假设[11]。
正态近似法和百分位数法的检验效能在样本量大的时候趋于一致,但在小样本时正态近似法明显优于百分位数法。由于百分位数法单纯的利用了Bootstrap样本的P2.5和P97.5信息,其计算置信区间原理属于一种非参数的方法,而正态近似法既利用了原始抽样样本中位数差值的真实差异又利用了Bootstrap样本的信息,根据中心极限定理计算其置信区间属于一种参数方法,故正态近似法的检验效能要优于百分位数法。临床判断非劣效性的一个重要问题是非劣效性界值Δ标准的选择[12]。本研究中,当把非劣效性临界值Δ设置为13、14时,三种方法的检验效能同时降低,但仍然是H-L法优于正态近似法和百分位数法。但由于H-L法的区间宽度最小且稳定,改变非劣效性临界值对其影响较小。
本研究主要针对以时间作为效应指标,且可能存在不确切值的右截尾数据,并以中位数作为比较的指标进行非劣效性检验。除本研究介绍的两类置信区间法外,也可以考虑选择生存分析的方法。但理论上针对右截尾的数据中位生存时间和时间的中位数是相等的,而且如果仍采用Bootstrap法估计中位数差的置信区间结果与本研究中使用的方法也应该是一致。Jinheum指出也可以利用分层Cox比例风险模型计算中位生存时间差的置信区间[13],但其标准误计算较为复杂。因此,针对右截尾时间数据计算中位数差值的置信区间,应首先考虑基于中位数差的Bootstrap法或H-L法。但如果数据中存在其他类型的删失数据,如研究对象中途退出等,此时中位数比较法已不再适用,应考虑利用分层Cox比例风险模型得到中位数差的置信区间。
从本次研究的结果来看,在药物的非劣效试验中,三种中位数差值的区间检验方法所获得的区间都包含了总体中位数的真实差异。整体来看,H-L法获得的区间最窄且最稳定,检验效能最高,且对极端值有较为稳健的处理,尤其在样本量不大时建议选择H-L法。其在实际应用中H-L法的操作复杂程度也要低于Bootstrap法。

