基于动力学性能的更高速度铁路合理线间距研究
付连著 李红艳 孙加林 李红梅
(1.铁科院(深圳)研究设计院有限公司,广东深圳518055;2.中国国家铁路集团有限公司铁路基础设施检测中心,北京100081;3.中国铁道科学研究院集团有限公司基础设施检测研究所,北京100081;4.中国铁道科学研究院集团有限公司铁道科学技术研究发展中心,北京100081)
铁路运输的高速化是世界各国铁路技术发展的方向。随着列车运行速度的提高,列车高速交会引起列车之间的气流剧烈扰动,产生的瞬态压力冲击对列车运行安全性和旅客舒适性带来不利影响。
为了分析列车交会时气动效应引起的动力学问题,相关学者开展了大量工作。何德华等[1]利用列车空气动力学和车辆动力学相结合的方法研究了动车组明线交会时气动力对车辆动力学的影响。王一伟等[2]研究了隧道压力波的形成和峰值影响因素,推导了压力极值对应的最不利隧道长度关于列车长度、运行马赫数的表达式。郗艳红等[3]提出了明线等速交会时车体表面压力波幅值变化的新公式。梁习锋等[4]研究了不同线间距下高速列车交会时的压力波特性。乔英俊等[5]阐述了线间距与列车交会压力波之间的理论关系,并根据实测和数值仿真数据得出了压力波与线间距之间的拟合曲线。魏洋波等[6]采用滑移网格技术对高速列车明线交会及隧道内交会时的空气流场进行数值模拟,研究了不同线间距对高速列车交会压力波的影响。
上述研究均基于既有线路的设计时速,不超过350 km。为了做好列车进一步提速的技术储备,有必要对我国高速铁路列车交会试验数据进行综合分析,研究列车进一步提速后的空气动力学效应和车辆动力学性能。本文建立了明线交会和隧道内交会的空气动力学模型及车辆动力学模型,研究不同车速、不同线间距条件下列车交会时所受的风压变化规律及其对车辆动力学的影响规律,为确定更高速度下的铁路线间距提供参考。
1 计算模型
1.1 空气动力学模型
选取CRH380A型列车作为研究对象,根据车辆实际结构,采用成熟的商业计算流体软件FLUENT建立三维实体列车空气动力学模型,如图1所示。建模时在计算精度允许的前提下,对车辆进行了适当简化。为了提高网格质量、计算精度和效率,全部部件均采用结构化网格。

图1 CRH380A型动车组三维实体空气动力学模型
列车交会属于非定常问题。为模拟交会列车之间的相对运动,计算区域采用分区对接网格技术,地面、列车均采用六面体结构化网格离散。各分区之间通过公共滑移界面进行数据交换。计算模型离散后的体网格总数均在1 000万以上。动车组明线交会及隧道内交会的空气动力学计算模型如图2所示。

图2 动车组交会空气动力学计算模型
1.2 车辆动力学模型
根据CRH380A型列车的实际结构,采用UM车辆动力学仿真软件建立车辆动力学模型。单编组车辆模型由1个车体、2个构架、8个轴箱、4个轮对构成,轮对和构架通过一系悬挂单元连接,构架与车体之间通过二系悬挂单元连接,如图3所示。

图3 车辆动力学模型(单编组)
1.3 动力学评价指标
根据GB/T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》,脱轨系数和轮重减载率的限值均为0.8;轮轴横向力H应满足H≤15+P0/3,其中,P0为静轴重,kN。
根据《高速铁路线路维修规则(征求意见稿)》,车体横向加速度不大于0.10g,车体垂向加速度不大于0.15g,Sperling平稳性指标控制在2.5以下,评级即为优秀。
2 模型验证
选取8编组CRH380A型动车组进行隧道内交会的实车试验。动车组长约203 m,线间距为4.4 m;隧道断面面积81.37 m2,长863 m。交会地点为隧道中心,车速v=300 km/h。
将实车试验的参数输入仿真模型进行计算,得出交会压力波时程曲线,并与实车试验结果进行对比,见图4。可知:仿真计算与实车试验的交会压力波变化幅值基本一致;实车试验的压力波变化曲线波动较大,这是因为实车试验考虑了车辆真实结构、列车振动、气候环境等因素的影响。

图4 隧道内交会的压力波时程曲线对比
仿真计算结果和实车试验结果吻合较好。因此,该仿真模型能够比较准确地反映动车组交会时的压力波变化规律。
3 工况分析
为充分考虑交会车辆之间的相互作用,建立8节车辆编组的动力学仿真模型。编组情况为:第1车、第4车、第5车、第8车为拖车,其余为动车。从车头到车尾均布64个监控点,监控点位于车窗高度位置。
将空气动力学仿真计算输出的力和力矩输入到车辆动力学模型进行仿真模拟,分析动车组在明线交会及隧道内交会时产生的空气压力波对车辆动力学性能的影响。
3.1 明线交会
动车组分别以v=350,400,450,500 km/h在明线交会时,车身风压随纵向位置的分布见图5。

图5 不同速度级下明线交会时车身风压分布
由图5可知,动车组以不同车速在明线交会时:①车辆全身所受风压最大值均出现在车头;②车头所受风压最大值均出现在车头前端,而车尾所受风压最大值均出现在车尾后端,这与车头和车尾复杂的形状有关;③车厢所受风压比较均匀,每节车厢所受风压最大值差别不大。
取线间距h=5 m,计算动车组以不同车速在明线交会时的车体表面平均风压,并拟合车体表面平均风压与车速的关系曲线,见图6。
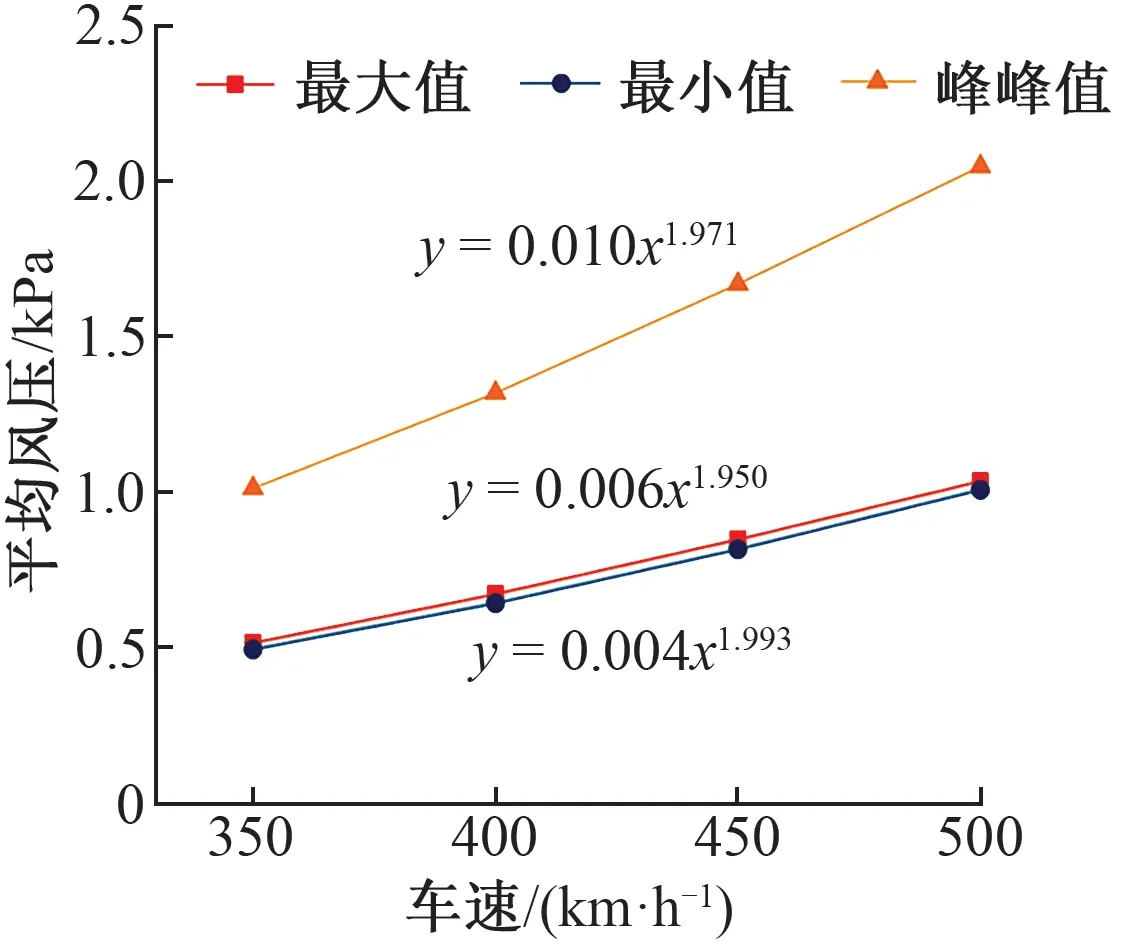
图6 明线交会时车体表面平均风压与车速的关系曲线
由图6可知,动车组在明线交会时:①车体表面平均风压的最大值、最小值、峰峰值均随着车速的增加而增大,v=500 km/h时车体表面平均风压的最大值、最小值、峰峰值比v=350 km/h时分别增大了106.6%,104.7%,102.4%;②车体表面平均风压与车速的2.0次方成正比。
分别取线间距h=5.0,5.2,5.4 m,计算动车组以v=500 km/h在明线交会时的车体表面平均风压,并拟合车体表面平均风压与线间距的关系曲线,见图7。

图7 明线交会时车体表面平均风压与线间距的关系曲线
由图7可知,动车组在明线交会时:①车体表面平均风压的最大值、最小值、峰峰值均随着线间距的增加而减小,h=5.4 m条件下车体表面平均风压最大值、最小值、峰峰值比h=5.0 m条件下分别减小了14.4%,12.3%,13.4%;②车体表面平均气动载荷与线间距的-1.5~-2.0次方成正比。
不同线间距条件下动车组以不同速度在明线交会时的车辆安全性、平稳性指标见表1、表2。可知:
1)同一车速条件下,车辆安全性、平稳性指标均随线间距的增大而减小。
2)对于v=350 km/h,动车组的各项指标在各线间距条件下均能满足要求;对于v=400,450 km/h,动车组在线间距h=5.0 m条件下能够安全平稳运行;对于v=500km/h,各线间距条件下均有动力指标超出安全限值。因此,建议动车组明线交会时的运行速度控制在450 km/h以下。

表1 明线交会时车辆安全性指标

表2 明线交会时车辆平稳性指标
3.2 隧道内交会
车速是影响动车组在隧道内交会时气动效应的主要因素之一。取隧道有效净空面积为100 m2,线间距为5.0 m。动车组以v=350,400,450,500 km/h在隧道内交会时,车身风压随纵向位置的分布见图8。

图8 不同速度级下隧道交会时车身风压分布
由图8可知,动车组在隧道内交会时:①车辆全身风压最大值出现在车头;②车头所受风压最大值出现在车头前端,而车尾所受风压最大值出现在车尾后端,这与车头和车尾复杂的形状有关;③车厢风压分布有一定差异,靠近车头的车厢所受风压最大,靠近车尾的车厢所受风压最小。
计算动车组在各速度级下进行隧道内交会时的车体表面平均风压和中心隧道壁瞬变压力,并分别拟合其与车速的关系曲线,见图9、图10。

图9 隧道内交会时车体表面平均风压与车速的关系曲线
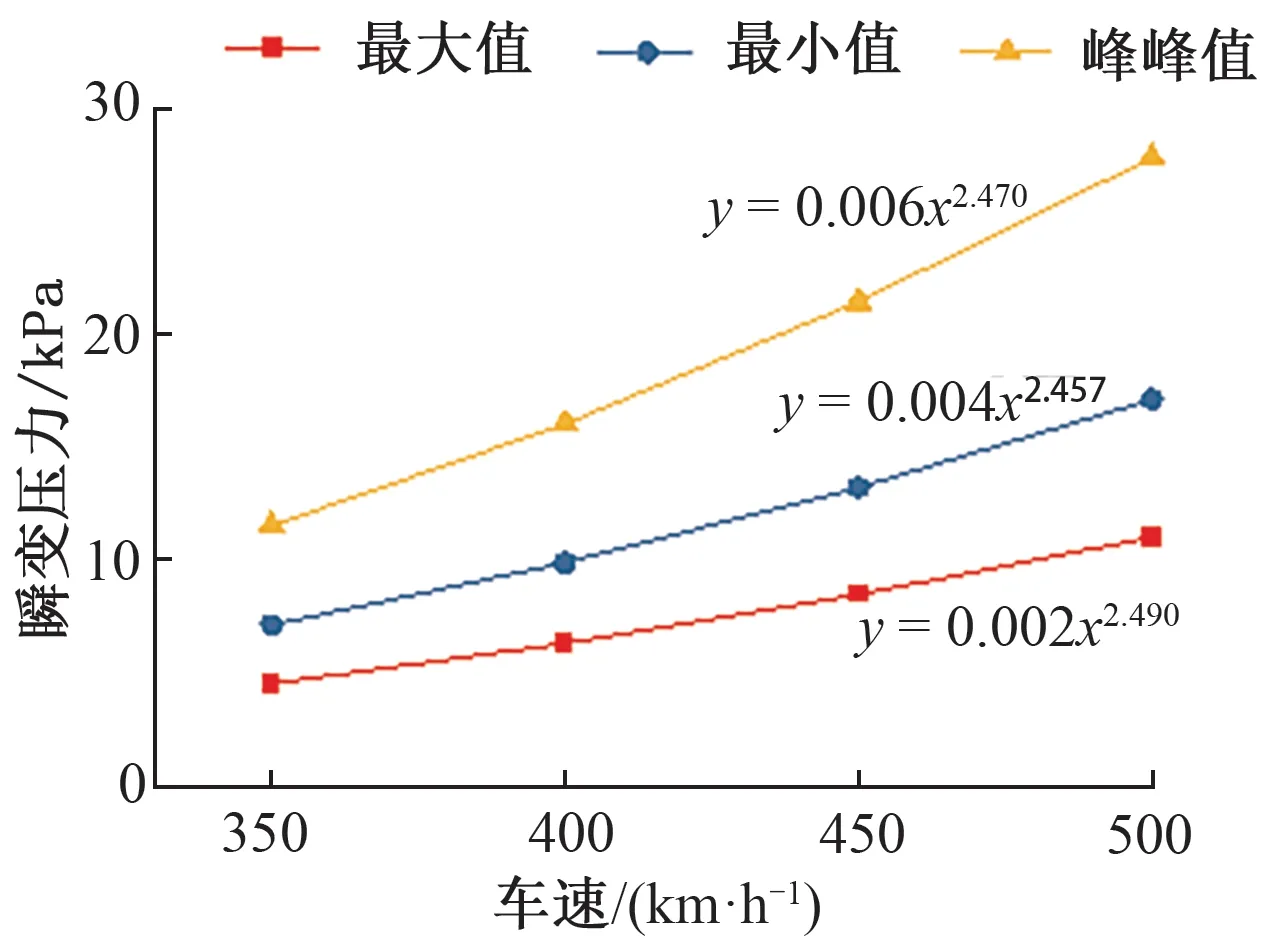
图10 隧道内交会时中心隧道壁瞬变压力与车速的关系曲线
由图9、图10可知,动车组在隧道内交会时:①车体表面所受的平均风压最大值、最小值、峰峰值与车速的2.3次方成正比;②中心隧道壁所受的瞬变压力最大值、最小值、峰峰值与车速的2.5次方成正比。
不同隧道断面面积、不同线间距条件下,动车组以不同速度在隧道内交会时的车辆安全性、平稳性指标见表3、表4。

表3 隧道内交会时车辆安全性指标

表4 隧道内交会时车辆平稳性指标
由表3、表4可知:
1)v=350 km/h时,动车组在各隧道断面面积及线间距条件下均能安全平稳运行。
2)在隧道断面面积为100 m2、线间距为5.0 m条件下,动车组以v=400,450 km/h在隧道内交会时各项安全性、平稳性指标均满足限值要求;v=500 km/h时脱轨系数、轮轴横向力满足安全性要求,而轮重减载率、车体横向加速度均超过限值,可能会发生瞬间晃车、脱轨等。
4 结论与建议
1)动车组在明线交会时,车头部位尤其车头前端所受风压最大,各车厢之间所受风压差别不大;动车组在隧道内交会时,车头部位尤其车头前端所受风压最大,车厢风压分布也有差异,靠近车头的车厢所受风压最大,靠近车尾的车厢所受风压最小。
2)动车组以350~500 km/h的运行速度在明线交会时,车体表面所受风压极值与运行速度的2.0次方成正比;动车组以350~500 km/h的运行速度在隧道内交会时,车体表面所受风压极值与运行速度的2.3次方成正比。
3)对于2种交会工况,相同速度级下的车辆运行安全性、平稳性指标均随线间距、隧道断面面积增大而减小。
4)考虑到车辆运行的各项安全性、平稳性指标限值及建设成本,对于设计时速350 km的线路,建议线间距取4.6 m;对于设计时速400~450 km的线路,建议线间距取5.0 m。

