地铁列车速度对扣件系统垂向动刚度的影响
栗尚明 杨麒陆
(1.中国铁建昆仑投资集团有限公司,成都610031;2.中铁建昆仑地铁投资建设管理有限公司,成都610031)
目前国内少数城市的地铁已采用时速120 km的设计运营速度,并且将陆续开通运营,新规划的地铁线路已普遍提高了设计运营速度[1-3]。列车提速后,其扣件系统垂向动刚度也会产生变化。这是因为扣件系统垂向动刚度主要由扣件胶垫提供,而扣件胶垫属于黏弹性高分子材料,这种材料的动刚度受加载频率影响较为明显[4-8]。更高的行驶速度给扣件胶垫带来更高的加载频率,若仍按设计刚度预测地铁列车行驶状况,可能对轨道结构振动特征分析甚至行车安全评估带来不利影响。
国内外许多学者对黏弹性高分子材料的频变特性进行了相关研究。文献[4-5]对树脂橡胶等材料进行了最大激振频率2 500 Hz的频变加载试验。文献[6-8]利用偏心振动试验台对黏弹性高分子材料频变刚度进行探索,并拟合出了该类材料动刚度随激振频率变化的经验公式。目前针对运营中地铁扣件动刚度的预测主要包括用实验室测试的静刚度乘以动静刚度比[9]、采用耦合计算方法[10]或动力计算方法[11-12]进行估算。前者预测结果的准确度不高,后者计算过程繁复。
本文基于一城市地铁GJ-Ⅲ型中等减振扣件系统现场测试结果,采用多刚体动力学软件建立车辆-轨道耦合模型。为了避免繁复的计算,推导出车速-扣件系统垂向动刚度经验公式并验证了其精准性。结合经验公式,利用仿真模型研究地铁列车速度对扣件系统垂向动刚度的影响。
1 现场测试
1.1 测点布置及测试内容
在里程YDK23+690处布设1个位移传感器,测试GJ-Ⅲ型中等减振扣件处的钢轨垂向位移。位移传感器得量程为±10 mm,测试精度为0.01 mm。测点布置如图1所示。

图1 测点布置
现场测试的试运营地铁列车为6节编组,全长122.2 m,为空载状态,空车轴重约80 t。
测试当天00:00—06:00共进行了6组空车试运营测试。每组2趟车,根据目前地铁运营常用的2种车速,设定测试行车时速分别为80,120 km。
1.2 测试结果及分析
各组测试结果差异不大,取其中具有代表性的一组进行分析。该组测试时,2趟列车时速分别为77,122 km,测试结果如图2所示。

图2 扣件处的钢轨垂向位移实测值
由图2可知,列车时速77 km时扣件处的钢轨最大垂向位移为0.818 mm,时速122 km时为0.755 mm,减小了7.70%。这是因为:①该地铁尚未开通运营,钢轨几乎没有磨损,车轮对钢轨垂向冲击荷载较小,此时轨道不平顺引起的垂向冲击荷载并非影响扣件处钢轨垂向位移的主要因素;②列车对扣件的加载频率与车速密切相关,当列车以较高速度通过时产生较高的加载频率,致使扣件胶垫垂向动刚度较大而钢轨垂向位移较小。
2 车辆-轨道耦合模型
利用多刚体动力学软件建立车辆-轨道耦合模型。
车辆部分由车体、2个转向架、4个轮对、8个定位转臂及连接装置组成,共50个自由度,如图3所示。其中,Kp,Cp分别为一系悬挂垂向刚度和阻尼;Ks,Cs分别为二系悬挂垂向刚度和阻尼;Kcy,Ccy分别为车体横向减振器刚度与阻尼;Cyaw为抗蛇形运动减振器阻尼。建模时采用现场测试车辆的参数。车体、转向架、轮对质量分别为21 920,2 550,1 420 kg。车体、构架点头转动惯量(垂向)分别为617 310,1 750 kg∙m2。车轮型面为LMA型面。

图3 车辆模型示意
钢轨采用中国60轨,密度为7 850 kg/m3,弹性模量为210 GPa,泊松比为0.25,纵向、横向惯性矩分别为3.22×10-5,5.24×10-6m4。
多刚体动力学软件中默认的钢轨为刚性钢轨,无法考虑钢轨形变与扣件系统的垂向刚度。因此,先利用有限元软件建立柔性钢轨模型,再通过多刚体动力学软件与有限元软件的接口程序将柔性钢轨导入多刚体动力学软件,最后以间距0.625 m添加扣件进行仿真计算[13]。
为提高计算效率,同时考虑相邻列车转向架对钢轨垂向位移的影响,车辆-轨道耦合模型中采用2节编组。
由于现场测试时钢轨几乎没有磨损,故轨道不平顺谱选用如图4所示的美国六级谱[10],不平顺波长为1~200 m。

图4 美国六级谱
3 经验公式推导及验证
采用多刚体动力学刚柔耦合建模,是一种基于模态叠加法的耦合计算方法,其计算过程相当繁复。为了简化计算,首先推导车速-扣件系统垂向动刚度经验公式。
文献[14]对钢轨扣件支反力进行了研究,得出轮对对扣件的加载频率f为瞬时车速v与转向架轴距lt的比值,即

扣件胶垫所受的动荷载源于列车通过时轮对施加到扣件上的荷载。扣件胶垫采用的橡胶材质不同,初始刚度也有差异,但其动刚度与加载频率在对数坐标系中均近似成线性关系[5,8]。
根据文献[7]给出的黏弹性高分子材料激振频率-动刚度经验公式,若已知车速为v0、加载频率为f0时黏弹性高分子材料的垂向动刚度为K0,则加载频率为f时垂向动刚度K的计算公式为

将式(1)代入式(2),即可得出车速-扣件系统垂向动刚度经验公式,即

本文所建立的多刚体动力学软件模型中设置的列车行驶时速为77 km。设计资料显示,该地铁测试段的GJ-Ⅲ型中等减振扣件轨道的扣件节点静刚度为10 kN/mm。根据文献[3,10],地铁扣件系统动静刚度比取1.2。因此,计算时扣件系统初始垂向动刚度取12 kN/mm。
利用基于多体动力学软件建立的车辆-轨道耦合模型对时速77 km工况下扣件处的钢轨垂向位移进行仿真试算。每次试算的动刚度增减量为0.5 kN/mm。当计算结果接近现场实测值时,每次试算的动刚度增减量改为0.1 kN/mm。
通过反复试算得出,当扣件系统垂向动刚度为15.5 kN/mm时,算得的钢轨垂向位移(图5)与实测值(图2(a))相差在0.5%以内。因此,时速77 km工况下扣件系统垂向动刚度可以取15.5 kN/mm。

图5 时速77 km工况下扣件处的钢轨垂向位移试算结果
已知lt=2.2 m,v0=77 km/h,K0=15.5 kN/mm,将v=122 km/h代入式(3),即可算得时速122 km工况下扣件胶垫的垂向动刚度K=16.46 kN/mm。
将v=122 km/h,K=16.46 kN/mm代入所建车辆-轨道耦合模型,对扣件处的钢轨垂向位移进行仿真模拟,结果见图6。

图6 时速122 km工况下扣件处的钢轨垂向位移仿真结果
由图6可知,仿真模拟得出的钢轨最大垂向位移为0.752 mm,与图2(b)的实测值误差仅为0.4%。这说明式(3)对扣件系统垂向动刚度的预测结果较为精确。
综上,只要知道一组车速及其对应的扣件胶垫垂向动刚度,就可通过式(3)预测不同车速下扣件系统垂向动刚度,避免了繁复的试算。
4 车速对扣件垂向动刚度的影响
利用式(3)分别计算列车时速60,70,80,90,100,110,120 km工况下的扣件系统垂向动刚度,结果见图7。

图7 车速与扣件系统垂向动刚度的关系
由图7可知,扣件系统垂向动刚度与列车速度正相关但非线性正相关,随着列车运行速度的增加,扣件系统垂向动刚度的增幅逐渐减小。
5 正常运营时钢轨振动特征分析
正常运营时,地铁列车时速约为120 km。正常运营后,钢轨磨损加剧,钢轨出现短波不平顺。因此,在美国六级谱基础上叠加中国铁道科学研究院针对我国短波轨道谱特点研究得到的波长0.01~1.00 m的短波不平顺[15]。
为对比是否考虑了车速对扣件系统垂向动刚度的影响给钢轨振动特征带来的差异,在进行仿真模拟时采用2种计算工况。
1)工况1:不考虑车速对扣件系统垂向动刚度的影响,扣件系统垂向动刚度按由静刚度10 kN/mm、动静刚度比1.2得出的结果(12 kN/mm)取值。
2)工况2:考虑车速对扣件系统垂向动刚度的影响,按经验公式的计算结果(16.46 kN/mm)取值。
将2种工况代入车辆-轨道耦合模型,得到扣件处的钢轨垂向振动加速度,见图8。

图8 2种工况下扣件处的钢轨垂向振动加速度对比
由图8可知,是否考虑车速对扣件垂向动刚度的影响,得出的扣件处的钢轨垂向振动加速度结果差别不大。
对2种工况下扣件处的钢轨垂向振动加速度进行三分之一倍频变换,结果见图9。
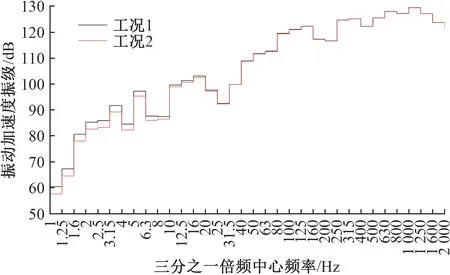
图9 2种工况下扣件处的钢轨垂向振动加速度振级对比
由图9可知:在钢轨垂向振动中心频率0~20 Hz内,工况2的钢轨垂向振动加速度振级明显小于工况1;钢轨垂向振动中心频率40 Hz以上时,2种工况几乎没有差别。可见,不考虑车速对扣件系统垂向动刚度的影响会造成在低频振动范围内高估钢轨垂向振动加速度振级,而是否考虑车速对扣件系统垂向动刚度的影响对中高频振动影响不大。
目前相关规范对扣件系统垂向动刚度动静刚度比的取值只给出了大致范围[9],列车在不同运营区段的行车速度也有差异。因此,建议在设计时考虑车速因素,利用式(3)进行估算,得出不同区段内较为准确的扣件系统垂向动刚度。
6 结论
本文基于一城市地铁GJ-Ⅲ型中等减振扣件系统的现场测试结果,采用多刚体动力学软件建立了车辆-轨道耦合模型。为简化刚柔耦合建模造成的繁复计算过程,首先通过分析轮对对扣件系统的加载过程,在黏弹性高分子材料激振频率-动刚度经验公式的基础上推导出了车速-扣件系统垂向动刚度经验公式,并验证了该经验公式可较为准确地估算列车运行速度变化时扣件系统的垂向动刚度。结合车速-扣件系统垂向动刚度经验公式,利用仿真模型研究了地铁列车运行速度对扣件系统垂向动刚度的影响,得出结论如下:
1)扣件系统垂向动刚度与车速正相关,但并非线性正相关。随着车速的增加,扣件系统垂向动刚度的增幅逐渐减小。
2)对于正常运营的地铁列车,若不考虑车速对扣件垂向动刚度的影响,会造成钢轨垂向振动中心频率在0~20 Hz内会高估钢轨垂向振动加速度振级。
由于目前研究模型的限制,本文从时域角度仅以轮轴激振主频作为输入,在今后研究中将从频域角度进一步讨论以宽频带振动作为输入的情况。

