子图融合修正WSN节点分布式定位算法*

赵 娜 刘松迪

辽东学院信息工程学院 丹东 118000

0 引言

随着航空航天技术的发展，航天设备的高性能、集成化和低功耗等要求以及航天作业环境的特殊性，使得传统有线电缆网络通信不仅影响设备的设计集成，还给系统的线缆布设、功耗带来巨大压力，无线传感器网络(Wireless Sensor Networks, WSNs)技术的出现恰好迎合航空航天发展的新需求，为设备通信、环境参量与健康状态监测、信息采集共享与协同作战开辟了新的思路[1]。

早在2003年美国在火箭动力系统中提出了分布式传感器网络，这些传感器能够实时地采集压力、温度等信息，并节点间协同运算完成检测与数据处理[2]；ESA和 NASA对多种应用于航天器WSNs的无线通信协议进行比较研究，得出适于航天器内部WSNs网络通信协议标准[3]；空间CCSDS在进行大量航天器WSNs网络技术的实验研究后，进一步验证了该协议[4]；国内在航天器WSN应用方面的研究起步较晚，哈尔滨工业大学等几个研究所共同设计了星内无线网络协议[5]；中国科学院设计了一个WSNs到总线的网关系统，应用于航天器内的环境监测[6]，并提出1553B-to-ZigBee网关设计[7]。目前WSNs已经在航天器上广泛应用，以美国为代表的发达国家已经在航天WSNs具体应用中取得巨大成果[2]，但我国WSNs在航天航空设置上的应用与研究还有很大差距，为此，航空航天设备WSNs技术也是我国现阶段航天技术的研究热点之一[8]。

实际航空航天应用中，节点感知可靠性及其自身定位精度是关系网络性能的重要指标，因此节点定位技术是WSNs在实际航天监控、预报和目标识别等应用环境的技术基础，影响着其采集信息的有用价值[9]。为此，仅部分节点加装定位模块，这些节点被作为位置信息已知的参考节点(Reference Node, RN)，而其他需实时定位的节点(Need to be Relocated Node，NRN)则通过最大似然估计等方法借助参考节点进行实时定位[10]。Kaur等[11]通过集中式的中央服务器对节点位置信息进行存储处理，具有较高的定位精度；叶娟等[12]通过设置多通信半径广播缩小重叠匹配及角度修正改进传统凸规划非测距定位算法；刘伟等[13]将正则项引入半正定规划松弛算法中，以减少算法中待优化参数的数量，同时通过梯度下降对松弛算法的位置信息进行细化；Slavisa等[14]将锥规划引入到分布式节点定位算法中，其每个NRN节点根据邻居位置二阶锥规划自身定位。Soares等[15]在最大似然估计算法中加入非凸松弛约束来描述节点定位，并通过共轭梯度法进行快速收敛定位。

在已有算法基础上，提出子图划分融合修正的分布式WSNs节点定位算法，算法在WSN无向图划分的基础上，首先在子图内通过相位搜索粗定位和遗传蚁群算法精定位提高单子图内未知节点的定位精度，然后通过子图间融合对位置进行修正，从而进一步提高节点定位精度，仿真实验验证了算法的有效性及其对不同规模的WSN网络的适应性。

1 WSNs节点定位算法

WSNs为多跳的自组织传感器网络，通常采用无向图G来表示，对于N个节点分布于[0,1]×[0,1]平面内的WSNs，其拓扑图可表示为G=(V,E)，式中，V={v1,v2,…,vN}为传感器节点集，其由随机部署的WSN节点的位置pi∈Rn决定，V为通信链路边集。

(1)

式中，(xi,yi)与(xj,yj)为参考节点坐标值，WSNs网络的各节点之间的欧氏距离可近似为

(2)

式中，列矩阵A，B，C和D可由单位矩阵派生，结合式(1)及RN节点的最小跳数nik，WSNs网络中的任意NRN节点k到RN节点i的距离为dik：

(3)

当RN节点数在3个或以上时，通过极大似然估计法或三边测量可估计出NRN节点位置。

传统RSS测距离通常根据WSNs节点发射和接收的信号的功率差计算[14]，但由于信号传输过程中存在多径效应等干扰存在，传统RSS测距并不准确，为此，将外界干扰导致的信号衰减合并到距离计算中，即

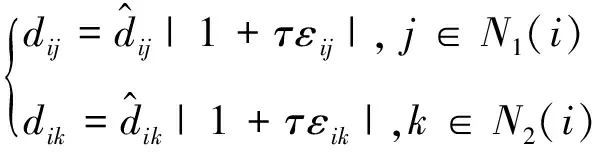
(4)

式中，εij和εik为用于描述信号衰减特性的随机噪声，其强度由τ∈[0,1]控制。

2 WSN节点分布式定位

在已有传感器节点分布式定位算法[11-12]中，通常为将定位算法分布到各未知参数节点中，由节点根据其邻居信息执行定位算法，这一方面不能充分发挥RN节点的性能，另一方面NRN节点的独立计算也增加了对RN节点的需求量，为此，文中将定位算法执行任务分布到各已知具有计算能力的节点中，根据连通和粗测距计算未知节点的精确位置。

2.1 子图内定位算法

根据RSS测距原理，传感器节点之间通信距离相对越远，其通信信号受噪声干扰越大，测距精度相对越低，因此，RSS测得的距离为一个估计值，存在误差，为此，在计算子图内节点定位时，主要目标为最小化原始RSS测距误差，根据节点通信距离计算加权权重值为：

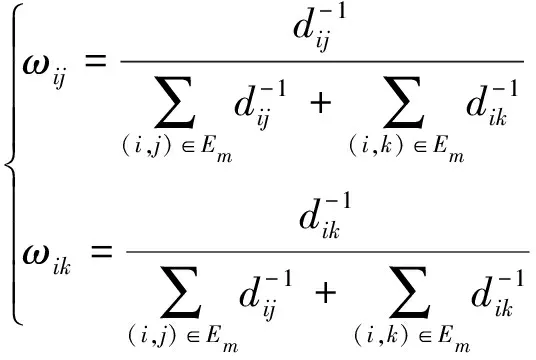
(5)

式中，dij与dik为WSN网络中节点间距离。根据节点距离及通信距离权重，改进子图内节点定位归结为一个距离误差加权值的无约束优化问题，其目标函数为：

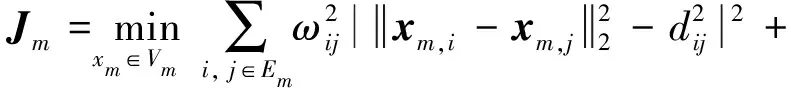
(6)

式中，amk与xmi分别表示RN节点与NRN节点在子图Gm中的坐标位置，将节点欧氏距离计算式dik与dij代入式(6)后，采用初始定位与精确优化相结合的两步法对目标函数进行优化求解。

2.2 基于相位搜索的初始粗定位

通过节点拓扑结构设计，可以保证每个未知信息的节点领域内至少有3个RN节点，NRN节点可以接收其领域内各节点的粗位置信息和粗略距离信息。这样，在进行NRN节点定位时，根据粗略位置，选取其领域内最接近的3个RN节点进行初始定位，其定位方法如图2所示，图中A、B、C为3个已知信息的节点，其坐标分别为(xA,yA)、(xB,yB)和(xC,yC)，P为待定位的NRN节点，设其坐标为(x,y)。

图1 基于RN节点的初始定位示意图

不失一般性，设参考节点信号初始相位均为0，当网络中噪声干扰较少可忽略时，RN与NRN节点间的连通信号为[12]：

(7)

式中，dn为节点间物理距离，其可由式(4)给出。由式(7)可见，在不考虑噪声干扰时，WSNs节点间信号相位与距离成正比。然而，当根据实测信号进行相位提取时，受相位缠绕影响，其会被限制在以波长λ为周期的主值(-λ/2,λ/2]内，影响未知节点定位准确性。当参考节点已知时，WSNs图任意虚拟像素单元(xi,yi,zi)与参考节点之间的信号可计算为：

(8)

式中，1≤n≤N，N≥3为未知节点相联通的参考节点数，可以看出，在存在噪声干扰情况下，当WSNs图中所计算的像素单元与真实未知节点越接近，计算的信号与真实信号越相似，为此，文中基于余弦相似性建立目标粗定位的目标函数。

余弦相似性基于向量模型的相似度分析方法，当向量夹角为0时，余弦值为1，两向量的完全相似。虚拟像素单元的信号相位与真实信号相位的夹角余弦值为

(9)

式中，Re{·}为取复数值的实部。根据未知节点的联通参考节点情况，将真实信号与虚拟像素单元信号重写为：

(10)

则基于余弦相似性的NRN节点粗定位目标函数可设置为：

(11)

式中，H为共轭转置符。当且仅当WSNs图中搜索虚拟单元与NRN节点重合时，式(11)存在最大值，NRN节点的粗定位转换为最大化目标函数的迭代优化问题，其初始值设置为N个联通RN节点的质心，即

(12)

2.3 未知节点迭代精确定位

(13)

1)根据式(1)和式(4)估计参考节点的平均跳变及距离，然后根据粗定位结果，确定未知节点的种群可行域，初始种群在该域中随机生成，则未知节点坐标(x,y)的上下界为：

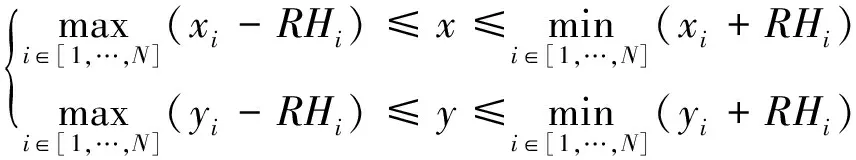
(14)

式中，(xi,yi)i∈[1,…,N]为与未知节点联通的参考节点的坐标。

(15)

(16)

式中:α≥0为路径参数，取值为α=1，β≥0为蚂蚁的可见性相关参数，其值为β=2;τij为t时刻节点(xi,yi)的残留信息量;ηij为节点(xi,yi)可见性，s∈{0,1}为下一选择状态。

3) 蚁群在WSNs的节点中遍历，并按式(15)更新各个可行路径的信息素τij，则遍历一次后

τij(t+1)=ρ·τij(t)+Δτij

(17)

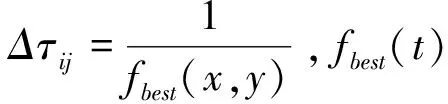
4)根据式(15)和式(16)不断迭代，直接满足迭代终止条件，则可以得到式(6)最优解，即得到未知节点的精确值。

2.4 子图间定位融合修改

以无向图表示的WSN拓扑结构被划分为多个具有重叠区域的子图Gm，各子图分别计算其NRN节点定位信息后，对重叠区域采用子图节点均值的方法进一步计算定位信息，以进一步修正NRN节点位置，并以修正值参与迭代子图内优化定位与子图间融合修正，其整个过程如图2所示。

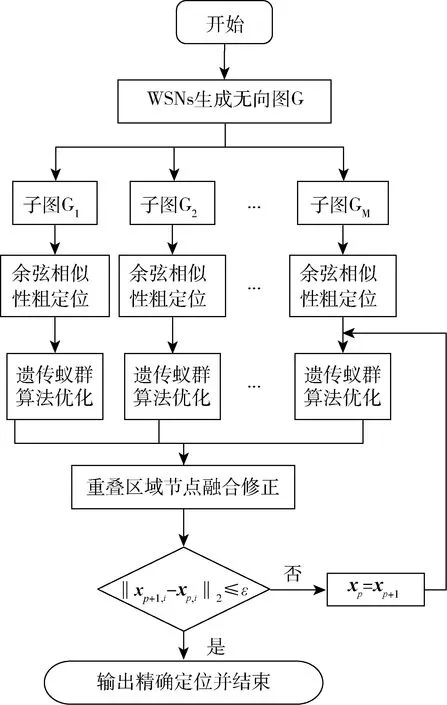
图2 分布式节点定位算法流程图

3 仿真校验分析

为验证算法的有效性和定位准确性，实验采用仿真数据方法进行算法性能验证，采用定位距离的均方根(RMSD)[12]作为评价指标，其计算式为

(18)

3.1 RN节点占比对算法性能影响

为验证算法在不同节点占比η=M/(M+N)下的定位性能，实验中通信半径dmax=0.60km，实验中不同占比下各算法得到的RMSD和时间如图3所示，图中结果为多次实验结果的平均值。

图3 不同占比下各算法的RMSD

从图3实验结果可以看出，随着η增大，松弛SOCP算法的实验结果变化最大，且随着RN节点占比的增加而减少，而文中算法与凸松弛算法的实验结果较为稳定，但如果RN节点过小，初始定位粗差过大，仍会影响文中算法的定位性能。同时算法在仿真实验过程中取得最小的平均RMSD值，说明文中算法的定位精度更好，这主要是因为文中算法每次迭代寻优过程中，计算子图内节点定位的同时，通过重叠区域的融合修正不断提高每次迭代的定位精度，从而保证最终精度最优。

3.2 不同通信半径对算法性能影响

在3.1节实验基础上，固定RN节点占比η=0.25，分析节点间的不同通信半径dmax对算法的定位性能影响，实验结果的平均值如图4～5所示。

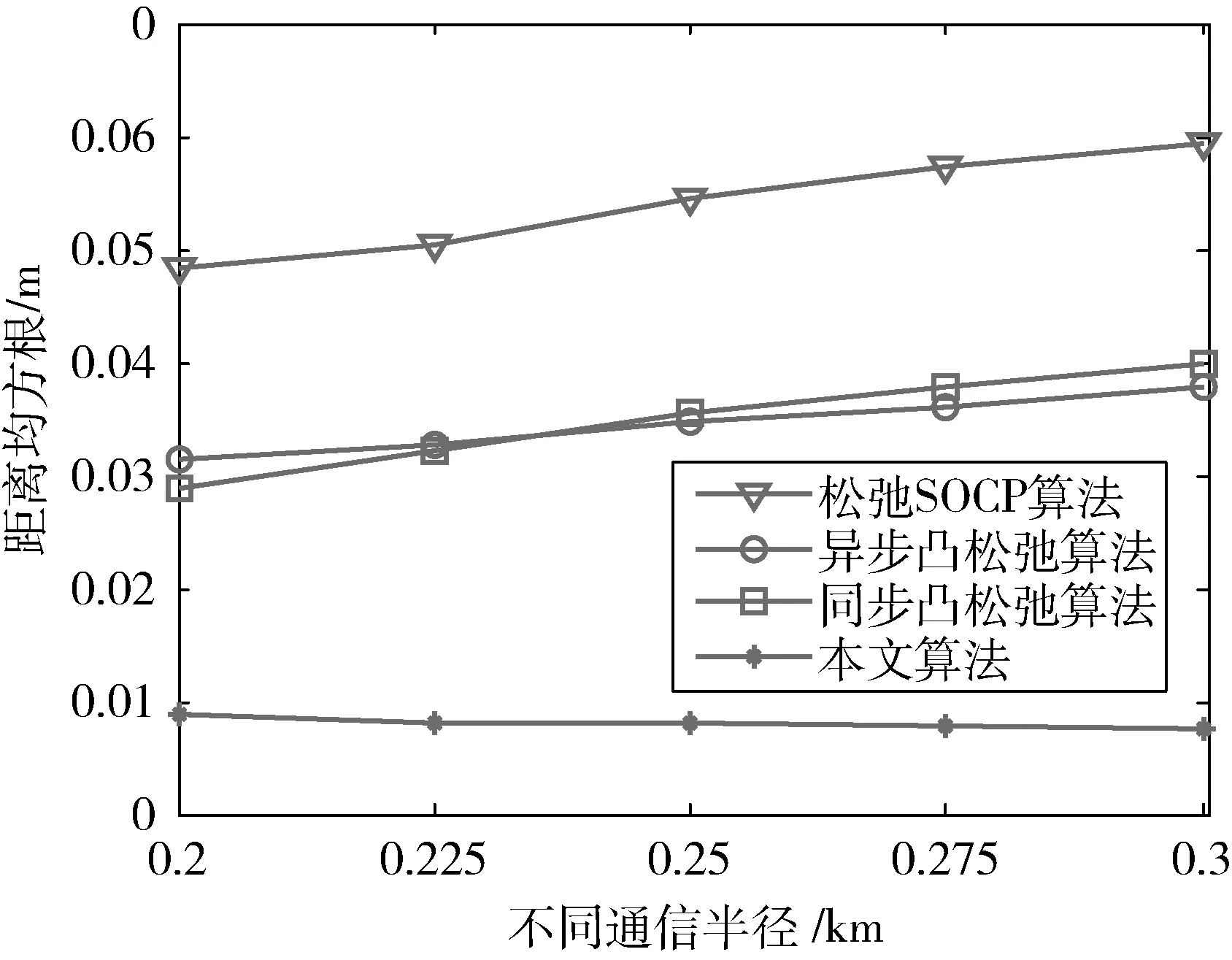
图4 不同通信半径下的RMSD

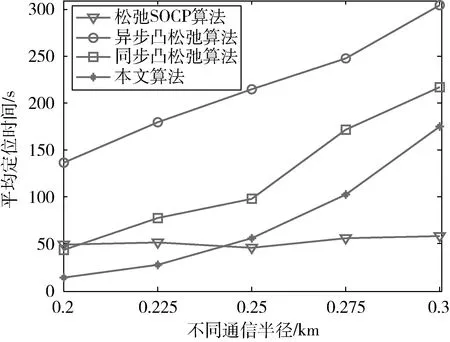
图5 不同通信半径下的平均定位时间

从图4～5所示结果可以看出，dmax的增大，文中算法的RMSD变化不明显，且始终保持最小值，而另外3种算法的RMSD都有不同程度增大，说明4种算法对通信半径变化具有较好的适应性，而dmax的增大，文中算法及2种凸松弛算法的定位时间随之增大，这主要是通信半径增大，节点间的RSS定位粗差增大，算法需要更多的迭代来弥补，同时节点的邻居节点也增多，通信量以及粗定位计算量也随之增大，因而定位时间随之增加。从图7整体看，在通信半径dmax<0.25km时，文中算法的定位时间依然最优，说明文中算法对RSS计算的粗定位有一定依赖性，实际使用时，应避免节点间通信半径过大。

综合实验结果可以看出，文中算法在满足计算要求的情况下，需要较少的RN节点或设置较小的通信半径即可获得较准确的定位精度。

4 结束语

针对大规模WSNs网络中节点的定准效率和定位精度问题，提出基于子图划分与图间融合修正的分布式定位算法，算法在WSNs子图划分基础上，首先在子图内通过相位搜索粗定位和遗传蚁群算法精定位提高单子图内未知节点的定位精度，然后通过子图间融合对位置进行修正，进一步提高节点定位精度。仿真实验验证了算法的有效性及其对不同规模的WSN网络的适应性。