基于强化学习的空间机械臂控制方法

李鹤宇 林廷宇 曾 贲 施国强

1. 北京电子工程总体研究所，北京 100854； 2. 北京仿真中心，北京 100854

0 引言

随着航天事业的不断发展，太空垃圾清理、航天器维修、装备组装成为研究热点。空间机械臂由于具有良好的适应性和扩展性，能够在复杂场景下，完成多种类型任务，被广泛应用于航天领域。针对空间碎片对在轨航天器的安全造成威胁的问题，使用空间机械臂捕获非滚转的目标[1-2]。SpiderFab计划采用7自由度的空间机械臂，通过人员遥控的方式实现全自主模式下的在轨制造与组装[3]。RAMST计划在地球轨道上，通过遥操作的方式实现模块化天基望远镜的在轨装配[4]。装配于国际空间站的双机械臂空间机器人系统Dextre、Robonaut2，利用双臂的协同性，能够执行更加复杂的任务[5-6]。

为使得空间机械臂应对复杂的任务需求，需要不断优化控制算法，提高系统的鲁棒性与精确性。文献[7]将末端执行器与目标相对速度的绝对值作为目标函数，使用最优控制的方法解决空间机器人捕获航天器的问题。文献[8]提出一种凸规划控制方法，用于控制空间机械臂捕获翻滚航天器。文献[9]建立碰撞避免模型，提出一种主动抑制干扰的控制算法，用于避免碰撞。文献[10]提出一种基于运动学的自适应控制方法，用于存在闭环约束和有效载荷惯性参数不确定的空间双机械臂控制问题。文献[11]使用绝对节点坐标法描述柔性体，建立末端带集中质量的双连杆柔性机械臂的动力学模型，采用PD控制策略实现了机械臂的运动跟踪控制。文献[12]运用非惯性系下的拉格朗日分析力学建立空间机械臂系统动力学方程，针对空间机械臂载体自由绕飞空间目标的情形，设计抓取目标的寻的制导控制规律。

随着计算能力的发展和数据资源的增加，用于决策问题的深度强化学习成为研究热点，出现DQN (Deep Q-network)[13]、DDPG (Deep Deterministic Policy Gradient)[14]、TRPO (Trust Region Policy Optimization)[15]、A3C (Asynchronous Advantage Actor-Critic)[16]、DPPO (Distributed Proximal Policy Optimization)[17-18]等算法。将深度强化学习应用于控制领域，产生了良好的效果。文献[19]对DDPG算法进行修改，并结合人工演示，使用深度强化学习控制机械臂完成插销入洞的任务。文献[20]在仿真环境中对TRPO算法进行训练，并将神经网络迁移至ANYmal机器人，实现四足控制。文献[21]不依赖于先验知识对PPO算法进行训练，并将训练结果迁移至多指灵巧手机器人，实现翻转立方体。文献[22]使用Q-learning的方法训练最大熵策略，并应用于实际机器人的操纵，实现较高的样本效率。

本文在虚拟环境中对神经网络进行训练，实现使用深度强化学习的方法控制空间机械臂，移动其抓手至物体下方特定位置。构建虚拟环境，包括5轴空间机械臂和目标物体，作为神经网络的训练环境，为算法提供数据支撑。设置状态变量表示当前环境信息，作为深度强化学习算法的输入，深度强化学习根据状态变量计算输出值，设置奖励函数对输出值进行评价，并由评价结果对神经网络的参数进行修改，实现学习过程。

1 PPO算法

在policy gradient算法中，神经网络的参数为θ，对应的策略为π，在一个完整的决策过程中，共包含T个步骤，神经网络不断与环境交互，形成序列τ：

τ={s1,a1,s2,a2,…,sT,aT}

(1)

式中：st∈Rn(t=1,2,…,T)为当前环境的状态向量，at∈Rm(t=1,2,…,T)为针对si神经网络的动作输出向量。由于神经网络在相同状态下可能得到不同的输出，因此序列τ发生的概率为：

(2)

式中：p(s1)为当前环境的初始状态为s1的概率，pθ(at|st)为环境状态为st、神经网络参数为θ时，输出为at的概率，p(st+1|st,at)的状态为st时，通过动作输出at得到新的环境状态为st+1的概率。

在策略为π时，神经网络能获得的期望奖励值为：

(3)

式中：pθ(τ)为神经网络参数为θ时，τ的概率分布，R(τ)为序列τ对应的奖励值。奖励对应的梯度为：

(4)

(5)

式中：θ′为收集数据的神经网络的参数，E(st,at)～πθ表示神经网络参数为θ时，由(st,at)计算得到的期望值，Aθ(st,at)为优势函数。如果θ′神经网络和θ神经网络在相同状态下得到的输出概率分布相差较大，则需要大量的采样才能保证算法的有效性，因此在目标函数中加入θ′神经网络和θ神经网络的KL散度，最终的目标函数为：

(6)

式中：β为KL散度的系数，DKL(θ,θ′)为参数为θ和θ′神经网络输出概率分布的差异。

2 基于PPO的控制算法

2.1 系统组成

本文致力于使用PPO算法对空间机械臂进行控制，完成将空间机械臂抓手移动至物体下方的目的。系统包括PPO算法和训练环境2部分，训练环境由空间机械臂和目标物体组成。设置合理的状态变量和奖励函数用于PPO算法和训练环境的交互，PPO算法根据模型的状态变量做出控制决策，奖励函数对控制决策进行评价，如果是好的控制决策，则通过调整神经网络的参数增加决策出现的概率，反之则通过调整参数降低决策出现的概率，系统结构如图1所示。

图1 系统结构图

2.2 训练环境

训练环境包括空间机械臂和目标物体2部分，物体位于空间机械臂正前方，空间机械臂包含5个关节，每个关节能够在[0°,360°)的范围内自由旋转，相邻关节间的连杆长度固定，通过控制关节的旋转，可以在有限范围内移动空间机械臂末端插盘式抓手至任意位置。

使用Unity设置空间机械臂每个连杆的长度、关节的旋转角度、底座的坐标、物体的中心坐标和尺寸，完成训练环境的构建。物体放置于固定的位置，空间机械臂每次初始化时每个关节保持固定的角度，界面如图2所示。在PPO算法的奖励函数中考虑碰撞事件，因此在Unity中使用盒子碰撞器实现碰撞检测功能，将盒子碰撞器加入到空间机械臂模型的各个部分监控碰撞事件，当发生碰撞时，碰撞器发出碰撞捕获信号和碰撞位置信息。

图2 仿真环境界面

2.3 基于PPO的控制决策算法

使用PPO控制空间机械臂进行运动，将抓手移动至物体下方，需要设置合理的状态变量和奖励函数，其中状态变量用于表示当前环境的信息，神经网络据此对空间机械臂进行控制，输出5个轴的转动角度，奖励函数对神经网络的控制决策进行评价，从而调整神经网络的参数，完成学习过程。

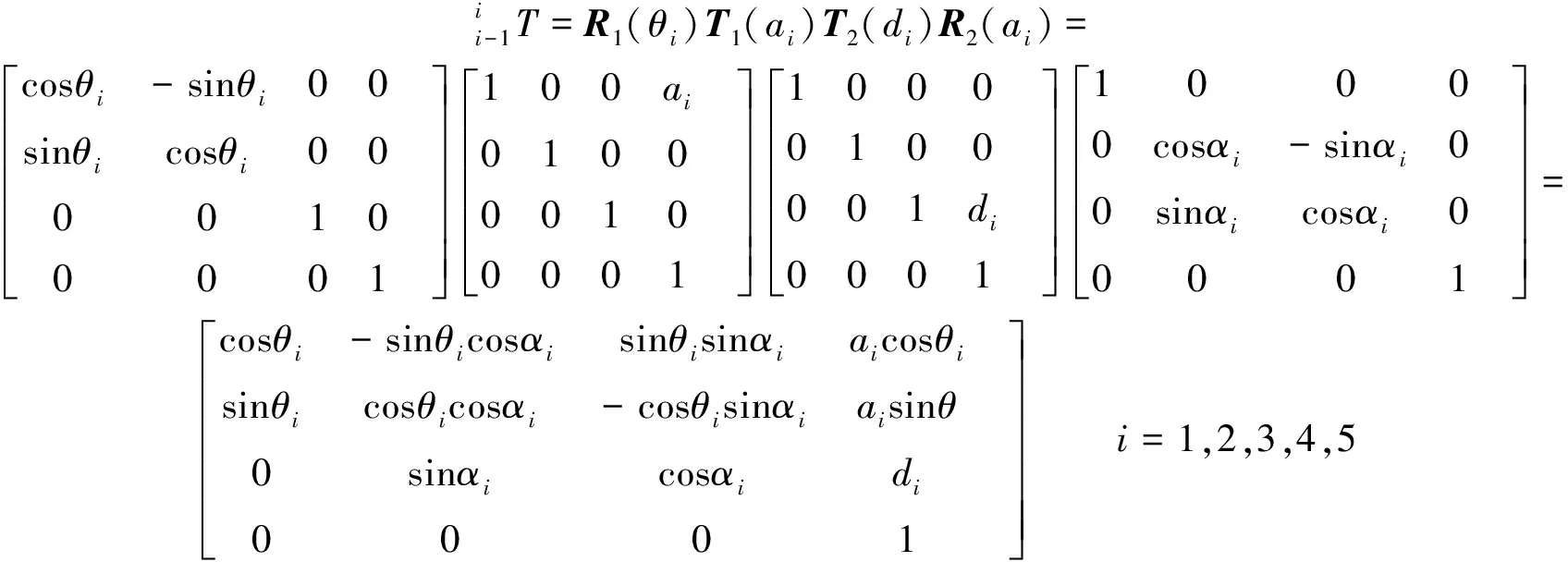
(7)

代表环境信息的状态变量共79维：

(8)

式中：jn为世界坐标系中原点指向空间机械臂关节中心的向量，ttarget为世界坐标系中原点指向目标物体中心坐标的向量，f为世界坐标系中原点指向机械臂基座中心的向量，tm为世界坐标系中原点指向物体下方选定点的向量，hm为世界坐标系中原点指向抓手上方选定点的向量，dcol为碰撞发生情况。

奖励函数分为2个阶段。第1个阶段引导空间机械臂抓手移动至物体下方特定位置：

(9)

(10)

第2阶段引导抓手从物体正下方向上移动至特定位置：

(11)

(12)

(13)

3 仿真校验

为验证本文算法的效果，从算法收敛时间、训练周期奖励值，以及神经网络参数收敛后机械臂抓手与物体下表面距离等方面进行对比。

对不同控制方法的收敛时间进行统计。传统控制方法需要根据特定任务进行调试，调试时间84.0h。训练所使用的计算机处理器为Intel(R) Core(TM) i5-9300H，显卡为NVIDIA GeForce GTX 1650，基于DDPG算法实现的机械臂控制算法的学习过程需要33.2h[23]，本文所使用的基于PPO算法的学习过程需要26.1h。相比于经典的控制算法，本文算法的学习过程能够节约68.9%的时间，相比基于DDPG的控制算法，本文算法的学习过程能够节约21.4%的时间。

其次，统计训练过程中每个周期得到的奖励值，如图3所示，横轴表示一次训练中的周期数，纵轴表示每个周期获得的奖励值。奖励值小说明该周期做出错误的控制决策，奖励值大说明该周期做出正确的控制决策。

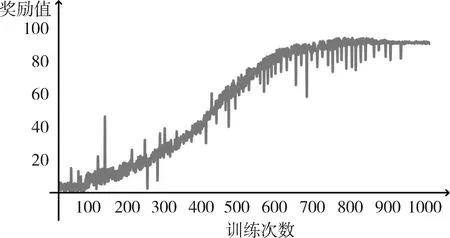
图3 三种系统突然加负载时的动态响应

由于PPO算法采用离线训练的方式，因此能够有效缩短数据积累阶段，在训练开始后，快速进入学习阶段。从图中可以看出，随着训练的进行，单个周期获得的奖励值逐渐增加，说明神经网络通过与环境的交互，利用奖励值正确地修改自身参数，逐渐做出正确的控制决策，最终奖励值趋于稳定，说明此时神经网络的参数收敛，达到稳定的控制效果。在训练过程中奖励值会出现波动，这主要是由于PPO算法在接收状态变量后，根据不同动作的概率得到输出，因此存在较小的概率输出错误的动作，即出现奖励值的波动。由于PPO通过神经网络生成一个关于不同控制决策的概率，因此在一个周期内，不一定会选择最优决策，因此曲线不是平滑的，会出现奖励值阶跃式变化的情况。

最后对比在训练完成后，即神经网络参数稳定时，基于DDPG的控制算法和本文算法的控制稳定性。统计30个控制指令中机械臂抓手与物体下方特定位置的相对距离，如图4所示，其中虚线代表基于DDPG的控制算法，实线代表本文算法，实线波动范围更小，说明训练完成后，本文算法能够达到更稳定的控制效果，因为对奖励函数的细化，有效抑制了控制中的抖动现象。

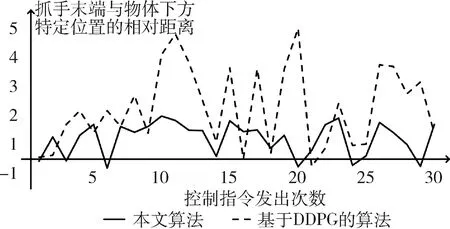
图4 机械臂抓手与物体下方特定位置的相对位置

4 结论

提出一种基于深度强化学习的机械臂控制算法。首先为深度强化学习搭建训练环境，包括机械臂和目标物体2部分，其次构建PPO算法，并设置合理的状态变量和奖励函数，用于神经网络的训练。通过验证，本文算法能够在较短时间内收敛，提高效率，并且具有稳定的控制效果，能够有效抑制抖动现象。