如何在“统一角度”下讨论风险配置类资产配置模型

周小燕 中国人民银行金融研究所博士后流动站

周萧潇 光大证券研究所

一、引言

资产配置（Asset Allocation）指的是，投资者通过权衡风险和收益，对资产配置不同的投资权重，以达到自身投资目的和风险收益目标的投资策略。为了能够满足新的投资需求，应对市场正在发生的新风险，资产配置方法也一直在日新月异地发展。

保险行业的负债特点决定了保险资产配置的目标是实现安全性、流动性和收益性的统一。资产配置是保险资金投资的重要一环。在风险可控的情况下高效地配置资产，对于推动我国保险资产管理行业健康发展、增强保险资金服务实体经济能力、发挥保险资金经济金融“压舱石”和“稳定器”作用具有重要意义。

一般而言，资产配置模型需要将一定的资产预测信息作为输入变量，通过模型的计算来确定最后的配置权重。在已有的资产配置模型中，我们可以通过需要预测的输入变量，将资产配置模型分为以下几类。

第一类为需要输入资产的收益预测信息和协方差预测信息的资产配置模型。1952年，Markowitz在《证券组合选择》一文中提出了经典均值—方差模型，这不仅标志着现代投资组合理论以及Markowitz 均值方差模型的诞生，也成为了现代资产定价理论的重要组成部分。

Markowitz均值方差模型的核心是，输入资产的预期收益和预期风险，来得到资产配置的有效前沿，通过最优化模型的方法从有效前沿上寻找对应的最优点。但模型找到的最优点往往无法完全达到投资者的投资预期目标，所以投资者们可以通过将效用函数的组成部分转移为约束条件的方式，使得最后的资产配置效果更加贴近自己的投资目标，其中，最具代表性的便是目标收益模型和目标风险模型。

为了克服传统均值方差模型的缺点，高盛提出以传统Markowitz 模型为基础的基于贝叶斯（Bayesian）理论的Black-Litterman 模型（BL模型）。BL模型将先验观点与历史均衡收益相结合，模型构建的投资组合不但是历史规律的总结，同时也反映了投资者的主观观点。当投资者对自己观点的信心水平较高时，组合收益接近主观预期收益，而信心较低时，组合收益反映市场均衡收益。

第二类为只需要协方差预测信息的资产配置模型，本文将这一类模型称为风险配置类模型。21世纪以来，资产收益率的难以预测和波动率的聚集效应，成为了推动资产配置发展的一个重要因素。通过对市场价格规律以及资产配置模型的实证结果的观察，投资者们发现在大多数情况下，我们对资产收益的预测是不准确的。但由于资产当月波动率与下月波动率存在非常强的相关性，即波动率聚集（Clustering）效应，我们对资产波动率的预测将更加准确。

在极端情况下，投资者为了追求投资组合风险最小化，经典的Markowitz均值方差模型可以转变为最小方差配置模型（Minimum Variance Model，MV）。最小方差配置模型通过去除收益的预期项，只对资产组合的波动率进行最优化配置，使得资产配置模型不再需要对资产的收益率进行预测。这一配置策略更加适合于风险厌恶型的投资者，但是在追求风险最小化中可能会使得投资组合收益较低，往往达不到投资者心里的收益预期。

最大分散度配置模型（Maximum Diversification Portfolio Model，MD）同样站在波动率配置模型的视角，追求波动率贡献最大分散化，但分散化定义式的分子部分忽略了资产之间相关性的影响，当资产之间存在较为明显的相关性时，导致实际应用效果不能真正达到对资产风险进行分散的目标。

除了以上两个波动率配置模型，由于人们往往偏好波动率较小的资产，避免投资波动率较大的资产，这样便形成了以波动率的倒数作为权重对资产进行配置的等波动率配置模型（Equal Volatility Model，EV）。等波动率资产配置法无需考虑不同资产间的相关性，也能使每种资产对投资组合的波动率贡献都是相等的，所以往往被看作是最为简单有效的波动率配置模型，但单个资产波动率的极值会使投资组合的配置结果产生偏差。

2008年全球金融危机以来，新兴的风险平价模型（Risk Parity Model，RP）和风险预算模型（Risk Budge Model，RB）正式登上资产配置的舞台。相比于其他模型，由于风险平价模型和风险预算模型是站在风险暴露程度的角度来配置资产，Booth 和Fama（1992）及Fernholtz 等人（1998）的研究均显示风险分散可以提高组合收益，进一步为风险平价策略的可操作性夯实了理论基础。虽然基于风险贡献的模型相比于其他模型对输入参数的准确度要求更小，但模型要求资产类别间的相关性较低，且模型往往高配债券，导致整体收益率较低。

前文介绍的风险配置类模型，虽然相比于均值方差类模型更能够起到控制波动、分散风险的作用，但也都存在各自的缺点。本文将以这一类型的资产配置方法为基础，通过构建统一的评价指标对它们进行分析，并提出一种新的改进风险配置类资产配置模型的方法。

除了上面介绍的两类资产配置模型，还有第三类不需要输入预测信息，而是基于投资者对宏观市场环境的观点来进行资产配置的模型，本文将这一类模型称为主观视角类模型。其中最为普遍的是等权配置模型（Equal Weight Model，EW），当投资者不使用量化模型来对资产最优权重进行估计时，等权配置模型能够在样本外获得比Markowitz 均值方差模型更高的夏普比率。此外，等权配置方法往往被视为其他资产配置模型的比较对象，本文通过将其他风险配置类模型的结果与等权配置模型的结果进行对比，对不同资产配置模型的波动率降低程度和资产分散化程度进行准确的判断。

除了等权配置方法，针对权益资产和债券的投资，市场上还有60-40、80-20 等固定权重的经典资产配置方法。由美林证券于2004年首次提出的美林投资时钟模型同样是现代长期大类资产配置框架中的重要理论，通过经济增长趋势、通胀水平的起伏将经济周期划分为4 个阶段，并探寻经济周期所处阶段与资产之间的轮换关系，周期性的资产配置方案常将美林时钟作为基础或参考。

二、构建风险配置类资产配置模型的统一评价指标

如同前文介绍的那样，不同的资产配置模型都具有自己的优缺点，但如何在同一维度上对不同资产配置模型进行比较，依旧是一个值得重点讨论的问题。为了能够找到统一维度的比较方案，本文将以Z.Cazalet 等学者在文章The Smart Beta Indexing Puzzle（2013）中提到的Smart Beta的比较方案为基础，构建用于比较风险类资产配置模型波动率降低程度和资产分散化程度的评价指标。

（一）分散化指标的构建

Z.Cazalet 通过对以往文章的归纳总结，将具有最优化模型的风险类资产配置方法进行了形式上的统一，把它们看作是仅对参数进行不同取值的同一类模型的典型代表，在这一节，我们将首先介绍风险类配置模型的统一表达式。

在市场不允许做空的情况下，由于MV模型往往在某些小波动资产上配置过大权重，投资者将对约束条件进行限定，以满足自己的投资要求（如前文介绍的目标收益模型）。当我们对资产权重进行约束时，MV模型有如下表达式：

其中，约束条件中的w∈C 对各资产的权重做出了更加严格的界定，被应用最多的界定方式为Herfindahl指标：

当我们只投资于单一资产时，H（w）=1，当我们采用EW 方法来进行资产配置时，H（w）=1/n。定义：

我们便可以将Dw（w）看作是衡量模型资产分散度的指标，当模型具有最大分散度，即采用EW 方法进行配置时，Dw（w）=1；当模型具有最小分散度，即只投资于1 个资产时，Dw（w）=1/n。若使用Dw（w）的形式来约束资产权重，MV模型可以转变为如下形式：

当c≤1/n 时，模型等价于不进行权重限制的MV模型；当c≥1时，模型等价于EW模型。这从另一个角度验证了MV模型是具有最小分散度的资产配置方法，而EW 模型是具有最大分散度的资产配置方法。更进一步地，由于σ（w*（c））是关于c 的递增函数，所以在理论上我们可以得到：σ（wMV）≤σ（w*（c））≤σ（wEW）。

Maillard（2010）等人证明了RP模型可以等价于如下的最优化问题：

其中，c∈（-∞,-n ln n]。与MV模型相似的，当c取-∞时，模型等价于不进行权重限制的MV模型，当c≥-nlnn 时，模型等价于EW模型。Maillard指出c 存在唯一取值，使得这一最优化模型与RP 模型等价，所以在理论上我们可以得到：σ（wMV）≤σ（wRP）≤σ（wEW）。

Dw（w）给出了基于方差的模型分散化指标，同样的，我们也可以给出基于风险贡献度的模型分散化指标：

其中，RCi=wi·（Σw）i/（w'Σw）1/2，且DRC（wRP）=1，即RP 模型的最优权重使得资产配置模型的风险贡献度最为分散。

从MDP 模型的表达式中，我们不难发现，MDP模型等价于如下的最优化问题：

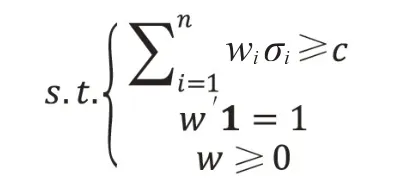
其中，c∈（0,maxiσi]。由于σi＞0，当c≤0时，模型等价于不进行权重限制的MV 模型。同时模型也存在c的唯一取值，使得这一最优化模型与MDP模型等价，所以在理论上我们可以得到：σ（wMV）≤σ（wMDP）≤maxiσi。如果将wiσi/（w'Σw）1/2看作是不同资产的波动率贡献度，我们同样可以得到基于波动率贡献度的模型分散化指标：

其中，DR（w）=（w'σ）/（w'Σw）1/2。

以上，我们将三个经典的风险类资产配置模型写成了相对统一的优化模型形式，并且基于三个角度构建了模型分散化指标，这三个指标将有助于我们对不同模型的分散度进行对比。

（1）基于资产权重的分散化指标：

（2）基于风险贡献的分散化指标：

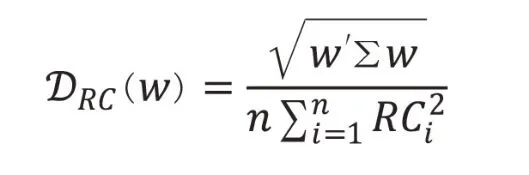
（3）基于波动率贡献度的分散化指标：

在本节接下来的部分，我们将基于这三个指标对几个模型进行对比，并且进一步构造能够对比波动率降低程度的指标。

（二）波动率指标的构建

定义了如何评价资产分散度的指标之后，我们还需要定义评价资产配置模型波动率降低水平的指标。在上一小节的公式推导中我们可以看到，EW 模型往往具有相对较大的波动率，所以我们可以将EW 模型给出的资产组合的波动率作为比较波动率降低水平的基准。为了评价波动率水平，在这一小节我们介绍几个指标的构建方法。

1.相对波动率指标

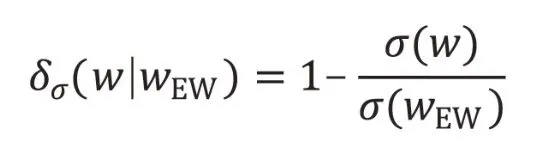
δσ（w wEW）越大，表示资产配置模型相对于EW 模型在波动率上降低得越多，反之则表示资产配置模型相对于EW模型在波动率上降低得越少，δσ（w wEW）为负表示资产配置模型的波动率大于EW模型的波动率。

2.条件波动率指标

σ（w wEW）表示资产配置模型相对于EW模型的超额波动率，同样可以作为评价一个资产配置模型波动率降低水平的指标。

3.波动率杠杆指标

β（w wEW）可以看作是一个杠杆指标，当资产波动率变动时，β（w wEW）代表了资产配置模型相对于EW 模型波动率的变化情况，β（w wEW）越大表示资产配置模型相对于EW模型对资产波动率变化的反应越敏感。我们同样将β（w wEW）作为评价一个资产配置模型波动率降低水平的指标。

三、风险类配置模型间的比较结果

（一）各风险类配置模型不同评价指标的特征表现及动态变化

在这一章，我们将举例对前文论述的几个评价指标进行验证。我们以上证50指数、恒生指数、黄金和中证国债作为目标资产，对它们进行资产配置。表1是以2020年7月31日为资产配置交易日，将4 个资产应用于4 个资产配置策略的权重分配结果，以及波动率降低指标和资产分散化指标统计表现。在资产模型中涉及到预期波动率的估计时，本文统一使用过去240 个交易日的资产滚动年化波动率作为估计值。

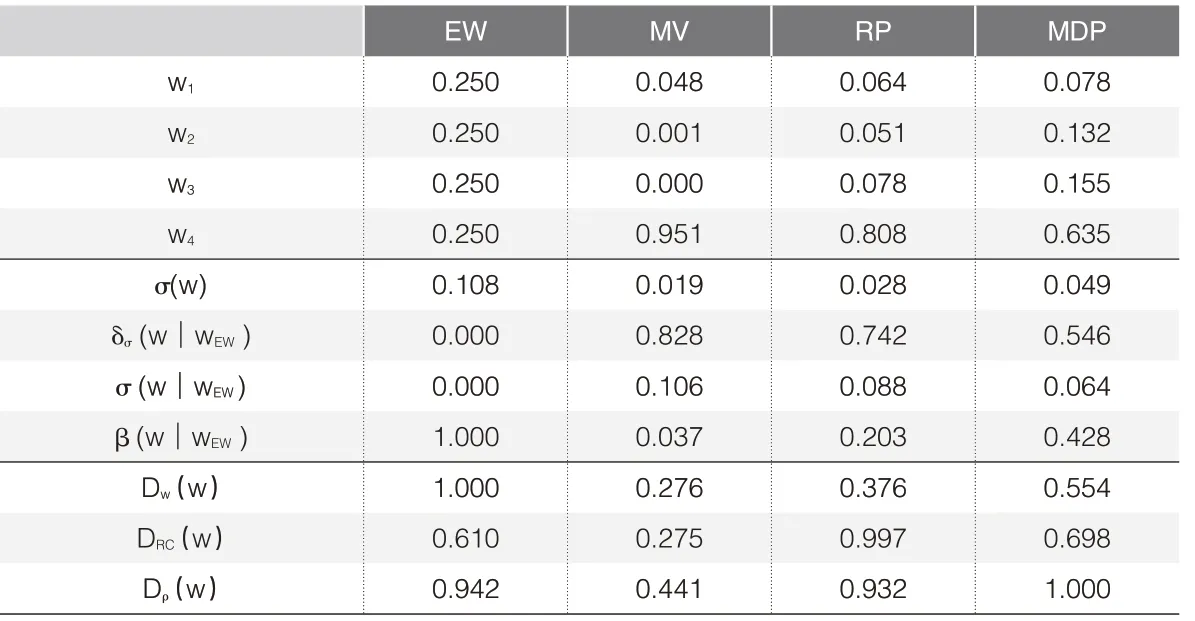
▶表1 资产配置策略的权重及各指标统计结果

表中第一层给出了每个资产配置模型得到的各类资产的最优权重。可以看到，除了EW模型，其他三个模型都将大部分资产分配给了中证国债。MV模型存在明显的投资过于集中的问题，RP模型和MDP模型虽然也将大部分资产分配给中证国债，但由于是站在风险贡献和波动率贡献的角度来配置模型，相比于直接以协方差来配置模型，它们更加贴合实际要求，更能够分散投资组合的风险。

第二层给出了每个资产配置模型在相对于EW模型在波动率降低水平指标上的表现。以EW 模型作为比较基准，其他三个模型的波动率明显都小于EW模型，MV模型具有最小的波动率，这与本文之前通过数学推导得到的结论保持一致。在δσ（w wEW）指标和σ（w wEW）指标的表现上，MV 模型更能够降低资产组合的波动率，MDP模型对降低波动率并没有十分显著，这与它以最小化投资组合波动率作为效用函数的初始目标并不吻合。在β（w wEW）指标的表现上，相对于EW模型，MV模型对资产波动率变化的反应敏感度很低，而MDP模型对资产波动率变化的反应敏感度最高，这说明，当资产波动率相比于预测值发生较大幅度的变化时，MDP模型最容易受到误差的影响，这也解释了为什么MDP 模型的波动率降低效果不明显的事实。

第三层给出了每个资产配置模型在三种资产分散化指标上的表现。EW模型在对资产波动率进行分散的角度上表现最好，RP模型在对资产风险贡献进行分散的角度上表现最好，MDP模型在对资产波动率贡献进行分散的角度上表现最好，这与前文的理论推导结果相吻合，说明这几个风险类资产配置模型确实能够表示成如前文所述的相对统一的最优化表达式。

（二）利用不同评价指标构建资产配置组合新思路

从指标构建的角度我们可以发现，将相对于EW 模型的δ（σw wEW）指标作为约束条件，对不同的资产配置模型进行最优化求解，我们可以更加直接地在EW 模型的基础上，利用其他的风险类资产配置模型提升资产组合的配置效果。

例如，以δ（σw wEW）指标作为约束条件的RP模型，能够在保持模型具有最大风险贡献分散程度的前提下，使得配置在各类资产上的权重更加分散，解决了模型在债券资产上分配过多权重的缺点；以δ（σw wEW）指标作为约束条件的MV 模型，能够在保持模型具有最小波动率的前提下，在各类资产上配置的权重更加分散，解决了将权重集中分配给波动率最小的资产的缺点。具体结果如表2、表3所示。

▶表2 资产配置策略的权重及各指标统计结果（δσ(w│wEW)=0.2）

为了进一步对各个风险配置类模型进行对比，我们固定不同的δ（σw wEW），来观察在每一个模型上各评价指标的动态变化情况。

▶表3 资产配置策略的权重及各指标统计结果（δσ(w│wEW)=0.1）

图1 展示了在MV 模型中，当我们固定不同的δσ（w wEW）时，各评价指标的动态变化规律。图中的橙色星号标记了表1中各模型的最优解的点，可以看到，图1中每一条紫色曲线都通过了直接求解MV模型得到的最优解点。随着δσ（w wEW）的增大，三个评价资产分散度的指标先增后减，而σ（w wEW）先减后增，说明四个评价指标在MV 模型中都存在最优值的点，而最优值的点并不是直接求解MV 模型得到的点，而在EW 模型和MDP 模型确定的δσ（w wEW）值区间内。与其他评价指标表现不同的是，β（w wEW）随着δσ（w wEW）的增大而减小，说明只需要δσ（w wEW）大于0，MV模型得到的资产组合关于波动率的敏感度便弱于EW模型。

▶图2 RP模型中不同评价指标的动态变化折线图

▶图3 MDP模型中不同评价指标的动态变化折线图

▶图4 以MV模型进行资产配置回测，不同评价指标的动态变化折线图

图2 和图3 则分别展示了在RP 模型和MDP 模型中，当我们固定不同的δσ（w wEW）时，各评价指标的动态变化规律，结果与MV模型相类似。

▶图5 以RP模型进行资产配置回测，不同评价指标的动态变化折线图

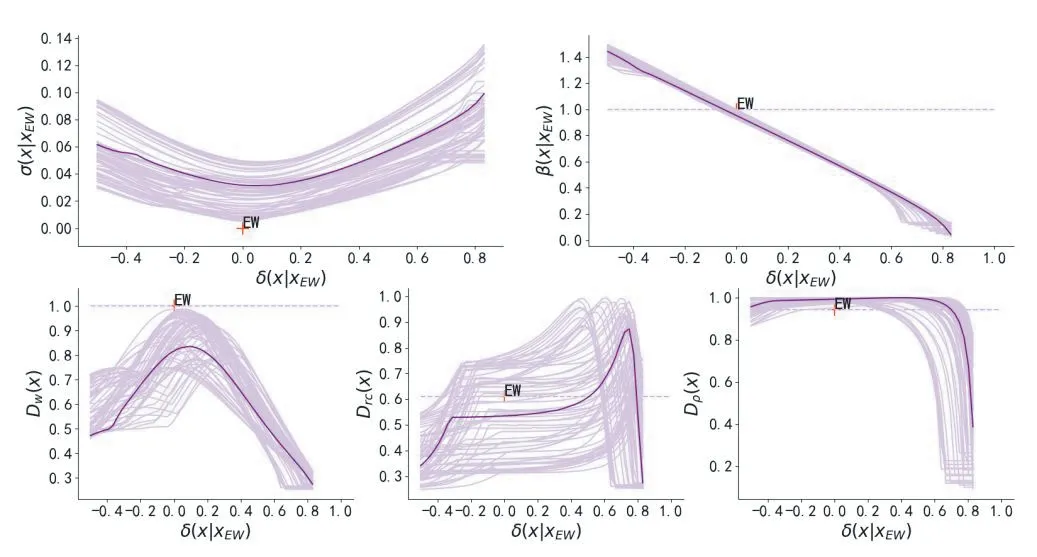
▶图6 以MDP模型进行资产配置回测，不同评价指标的动态变化折线图

（三）风险配置类模型的回测表现

上一节中，我们主要在2020年7月31日这一时间点对各模型进行比较分析，但并没有将各模型引用到滚动时间的回测当中。在这一节，我们将会从实际操作的角度出发，对四个资产配置策略进行回测。

▶图7 四个资产配置模型的净值曲线

▶图8 四个模型各资产累计权重图

我们仍以上证50指数、恒生指数和黄金作为风险资产，以中证国债作为无风险资产，在每个交易日以过去240个交易日的收益率来估计资产波动率，并在每个月的最后一天重新确定各资产配置模型中的资产权重。回测时间为2010年2月1日到2020年7月31日。

在分析回测结果前，我们先来对上一小节介绍的各风险评价指标的动态表现做一个时间序列上的纵向比较。以图4 为例，图中深紫色曲线为7月31日MV模型各风险评价指标的动态变化曲线，浅紫色为回测时间内过去每个月最后一天各风险评价指标的动态变化曲线。可以看到，各指标的变化规律在时间序列上也是完全统一的，说明我们在上一节得到的结论具有一般性，并非特例。图5 和图6 展示的RP 模型和MDP 模型也有相同的表现。

图7 给出了2010年2月1日 到2020年7月31日四个模型的资产配置结果净值曲线，可以看到，EW 模型相比于其他三个模型确实有更高的收益波动，但MDP模型的收益波动也高于另外两个以风险贡献度和资产波动率作为优化目标的资产配置方法，这说明MDP模型虽然以资产波动率作为优化目标，但忽略了资产之间存在的相关性，并不能很好地避免资产组合产生较大回撤。RP 模型和MV模型的回测结果较为接近，但RP模型在控制波动上优于MV 模型，这说明以风险贡献度作为优化目标，确实能够忽略更多协方差估计中存在的误差。

图8给出了四个资产配置模型在全回测区间内的资产累计权重图，EW 模型将权重平均分给了四个资产，而MDP模型在各资产上的权重分配也较为平均。RP 模型和MV模型将大部分资产分配给了中证国债，特别是MV模型将几乎所有的权重都分配给了中证国债。