钢筋锈蚀产物纳米压痕的分子动力学模拟

徐亦冬， 陈 坚， 方建柯， 毛江鸿

(1.浙大宁波理工学院 土木建筑工程学院， 浙江 宁波 315100； 2.长江科学院 水利部水工程安全与病害防治工程技术研究中心， 湖北 武汉 430010； 3.江苏科技大学 土木工程与建筑学院， 江苏 镇江 212003； 4.重庆交通大学 土木工程学院， 重庆 400074)

沿海混凝土结构在服役过程中受氯离子的侵入，易导致钢筋锈蚀，其锈蚀产物主要为Fe3O4、Fe2O3、FeOOH和FeO[1-2].锈蚀产物体积膨胀所产生的锈胀力会挤压钢筋周围的混凝土，从而导致混凝土构件开裂破坏[3-4].影响钢筋锈胀力的内部因素主要有锈蚀产物的弹性模量和钢筋的锈蚀率[5-8].基于锈蚀产物弹性模量的重要性，许多研究人员对此进行了研究.如Oliver等[9]提出了1种根据压头载荷-位移中的数据来测定试件硬度和弹性模量的改进方法.Ouglova等[10]基于Hertz理论的固结试验，发现锈样的弹性模量随着压实程度的增加而增大.Bhargava等[11]直接假定锈蚀产物的弹性模量与钢筋相同.Caré等[12]采用弹性力学方法设计了空心圆柱模型，并结合电化学腐蚀试验，发现铁锈弹性模量随时间增加而增大.Zhao等[13]使用纳米压痕仪对自然环境和实验室环境下的锈蚀产物进行纳米压痕试验，得出铁锈弹性模量值处在102GPa数量级的结论.Nicholls等[14]基于共振频率技术，测量了钢筋锈蚀产物的硬度和弹性模量，其中弹性模量值在151～192GPa之间.

当前，确定钢筋锈蚀产物弹性模量的方法主要有纳米压痕和共振频率等测试技术.尽管测试结果整体处于100～200GPa之间，但由于试验制样过程较为繁琐，且研究人员所采用的试验方法和试验环境有所不同，其差值仍为数十GPa.目前，数值模拟技术不断发展，已成为材料科学研究中不可或缺的技术手段.如方建柯等[15]利用分子动力学软件计算了锈蚀产物主要晶体组分的弹性模量，并根据各晶体含量加权得到锈蚀产物的弹性模量，但是该方法并未建立锈蚀产物的真实模型.已有学者基于分子动力学方法开展了材料微观力学性能的纳米压痕模拟[16-19]，但锈蚀产物的弹性模量是否可以通过纳米压痕数值模拟计算得到，是值得研究的课题.

鉴于此，本文首先通过X射线衍射(XRD)测定钢筋锈蚀产物的组成与含量，进而构建锈蚀产物的微观模型；然后利用Lammps软件进行纳米压痕模拟，并利用Ovito软件对模拟结果进行处理；最终根据荷载-位移曲线得到钢筋锈蚀产物的弹性模量.

1 钢筋锈蚀产物模型纳米压痕试验

1.1 模型建立

1.1.1原材料

水泥采用P·O 42.5级普通硅酸盐水泥；水为自来水；细骨料为中粗砂；粗骨料为5～15mm碎石.混凝土配合比m(水泥)∶m(水)∶m(砂)∶m(碎石)=1.00∶0.53∶2.00∶3.00.钢筋混凝土试件尺寸为150mm×150mm×550mm，保护层厚度为25mm，其中纵筋采用2根φ10×500mm的HPB300钢筋.试件标准养护28d后，采用恒电流法加速试件中钢筋的锈蚀，得到锈蚀时间分别为6、9d的2组钢筋锈蚀产物试样(试样编号A和B).采用XRD对2组试样进行物相分析，得到钢筋锈蚀产物的衍射图谱；并计算4种锈蚀产物的含量(质量分数).表1为不同锈蚀时间下钢筋锈蚀产物的含量.

表1 锈蚀产物的含量

由表1可知，钢筋锈蚀产物主要由4种物质组成，但是不同锈蚀时间下钢筋4种物质含量有所变化.目前，对于4种锈蚀产物的分布(如层与层是否均匀叠加、是否非均匀混合等)尚无定论.因此，本文假设锈蚀产物的每层都是均匀的.首先建立每种锈蚀产物的结构，然后根据表1中每种锈蚀产物的含量，进行层层叠加，最终建立锈蚀产物的微观模型.具体步骤如下：

(1)通过分子动力学软件Material Studio生成单个Fe3O4、Fe2O3、FeOOH、FeO模型，优化后得到各自的稳定结构；再分别将Fe3O4、Fe2O3、FeOOH、FeO扩充为3×3×1、5×5×1、8×2×1、4×4×1的超晶胞.

(2)在微观尺度上，每种锈蚀产物的含量具体表现为每种锈蚀产物分子个数的比值.因此，根据表1中各锈蚀产物的含量，将其转化成4种物质分子个数的比值，并据此建立钢筋4种锈蚀产物真实含量的微观模型.

(3)利用Build Layer工具将各锈蚀产物进行层层叠加，生成2组锈蚀产物(试样A和B)的微观模型(见图1).为满足纳米压痕试样的尺寸要求，将微观模型扩充为3×3×1超晶胞.

(4)对模型进行结构优化.首先通过能量最小化进行优化，当能量达到最小且收敛值达到标准后，优化结束；随后进行分子动力学优化，使结构的温度和能量都达到平衡，最终得到稳定结构.

(5)将已建立的2种锈蚀产物模型分别导入Lammps软件中，然后在待测样上方0.2nm处放置1个直径为3nm的半圆形金刚石压头，如图2所示.需要说明的是，压头选用金刚石的原因是其弹性模量远远大于锈蚀产物的弹性模量，在模拟过程可假定压头为刚体，其弹性模量不会随着压入深度的变化而变化.

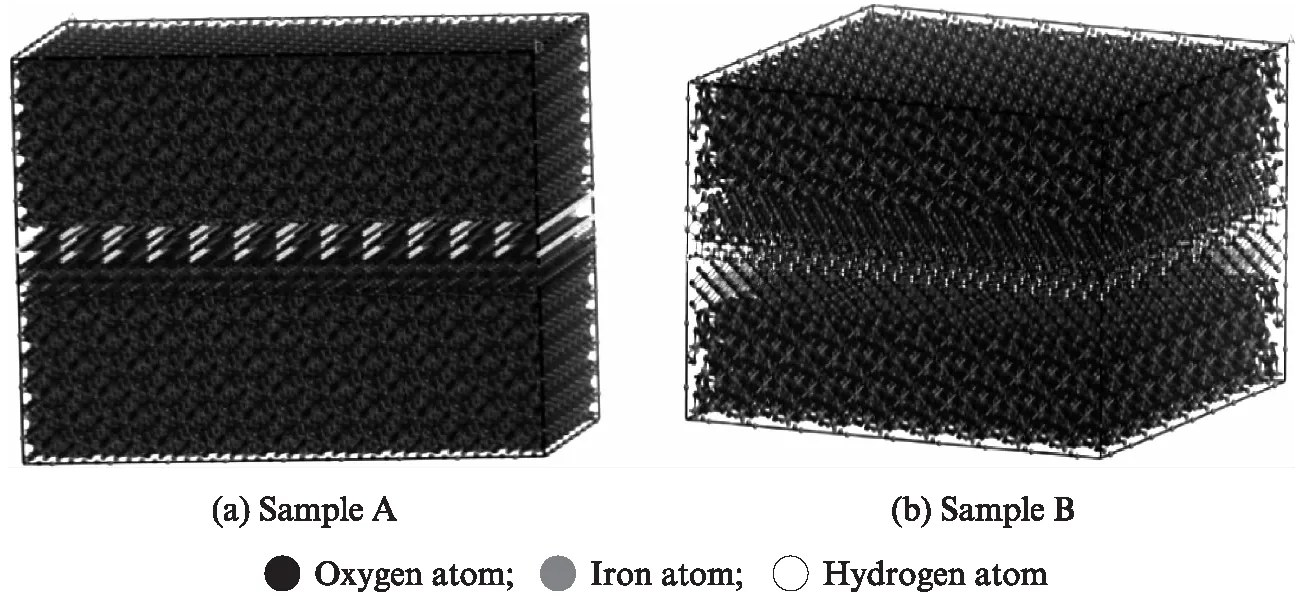
图1 层层叠加的锈蚀产物微观模型Fig.1 Microscopic model of corrosion products mixed layer by layer

图2 锈蚀产物纳米压痕模型Fig.2 Nanoindentation model for corrosion product

1.2 模拟过程

在纳米压痕模拟过程中，待测试件从内到外被分为牛顿层、恒温层和固定层[20].其中牛顿层中原子符合分子动力学基本原理，即经典牛顿运动定律运动；恒温层中通过改变原子速率的方法来保持原子温度不变；固定层中原子在x、y、z3个方向上保持固定，不随模拟时间而变化.

模拟时将时间步长取为1fs，具体步骤如下：(1)金刚石压头在待测试件上方0.2nm处，以5nm/s 的速度压入待测试件；(2)当压入深度达到0.2nm后，停止运动；(3)将金刚石压头以5nm/s的速度拔出；(4)当金刚石压头移至待测试件上方0.4nm处时，停止模拟.

整个压痕过程主要分为压头靠近基体、压头压入基体、压头拔出基体3个阶段[21].利用Ovito软件对模拟过程进行可视化，如图3所示.

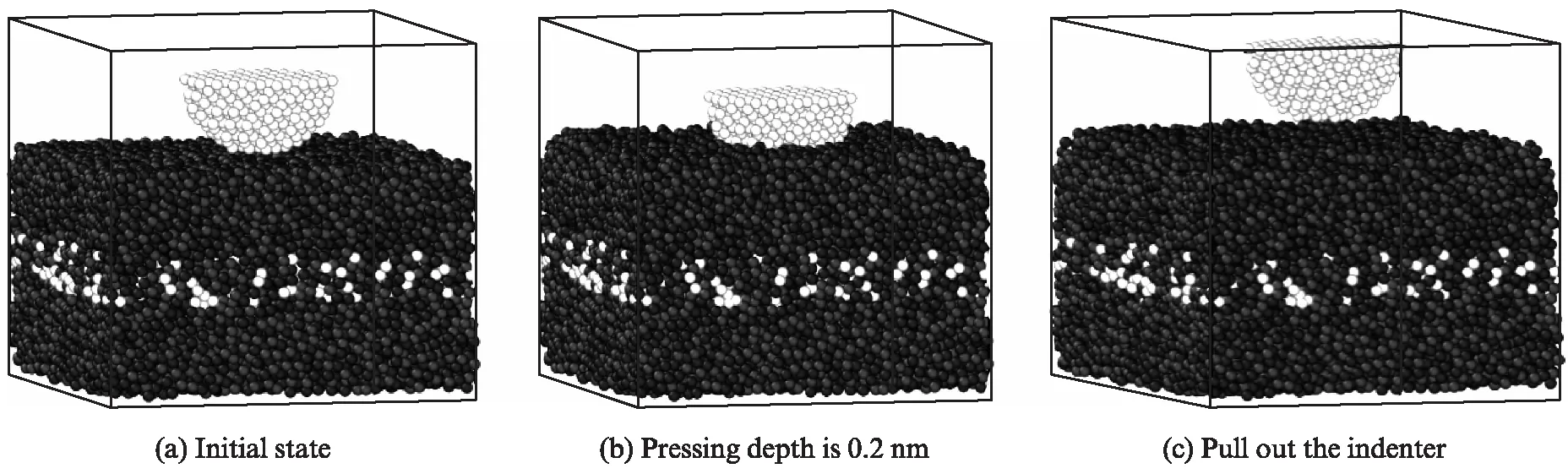
图3 纳米压痕模拟过程Fig.3 Nanoindentation simulation process

2 结果与讨论

2.1 荷载-位移曲线

通过Lammps软件得到输出变量.计算在不同压入深度下压头所受荷载(P)，最终得到压头所受荷载与压入深度(位移)之间的关系曲线，见图4.将模拟所得荷载-位移曲线与纳米压痕的典型荷载曲线[9]相对比，发现两者趋势基本保持一致.

2.2 弹性模量计算

为了根据荷载-位移曲线获得钢筋锈蚀产物的弹性模量，采用Oliver等[9]提出的钢筋锈蚀产物的弹性模量计算公式：

图4 纳米压痕荷载-位移曲线Fig.4 Load-displacement curves of nanoindentation

(1)

式中：Er为压头的缩减弹性模量；E为钢筋锈蚀产物的弹性模量；v为钢筋锈蚀产物的泊松比；Ei为压头的弹性模量；vi为压头的泊松比.

由式(1)可知，若要计算待测试样的弹性模量，需要先确定压头的泊松比、弹性模量、缩减弹性模量和待测试样的泊松比.其中，金刚石压头的泊松比和弹性模量为已知量，分别为0.07、1100GPa；另外，根据Zhao等[13]得出的钢筋锈蚀产物泊松比0.2和0.3对其弹性模量影响非常小的结论，本文将待测试样的泊松比取为0.25.

为了获得压头的缩减弹性模量，采用Beegan等[5]提出的压头缩减弹性模量与待测试样接触刚度之间的关系：

(2)

式中：s为待测试样的接触刚度；β为修正系数；A为压头与待测试样接触区域的投影面积.

根据式(1)、(2)，对钢筋锈蚀产物纳米压痕试验得到的荷载-位移曲线进行最小二乘法拟合,计算得到待测试样的弹性模量，结果见表2.由表2可以看出，钢筋锈蚀产物弹性模量在240～270GPa之间，大于钢筋自身的弹性模量200GPa，可能是假设的锈蚀产物排列方式为层层叠加方式所致.

表2 层层叠加锈蚀产物的弹性模量

2.3 模型修正

基于2.2节的分析，对原模型进行修正，假设锈蚀产物由4种锈蚀物质非均匀混合形成.建模步骤如下：(1)利用Amorphous Cell Calculation工具，将4种锈蚀物质模型按照表1中各锈蚀产物的含量随机混合，生成2组工况下锈蚀产物的微观模型；(2)为满足纳米压痕的试样的尺寸要求，将模型扩充为2×2×2超晶胞，随后对锈蚀产物微观模型进行结构优化，最终得到稳定结构，结果见图5.

图5 非均匀混合锈蚀产物微观模型Fig.5 Microscopic model of non-uniform mixed corrosion products

同样地，将建立的2种锈蚀产物模型分别导入到Lammps软件中进行纳米压痕模拟，得到2组荷载-位移曲线，见图6.

图6 非均匀混合锈蚀产物模型纳米压痕模拟荷载-位移曲线Fig.6 Load-displacement curve of nanoindentation simulation for non-uniform mixed corrosion products

根据式(1)、(2)得到2组非均匀混合锈蚀产物的弹性模量，结果见表3.

表3 非均匀混合锈蚀产物的弹性模量

图7 钢筋锈蚀产物试样B的扫描电镜照片Fig.7 SEM photo of corrosion product for sample B

前已述及，Zhao等[13]使用纳米压痕试验得出铁锈弹性模量值为102GPa数量级；Nicholls等[14]使用共振频率技术测量得到钢筋锈蚀产物的弹性模量在151～192GP之间.由表3可知，修正后的模型模拟结果分别为160.9、163.3GPa，处在160～170GPa 之间，与文献[13-14]已有结论较为吻合，验证了修正后模型的有效性，说明基于分子动力学的纳米压痕模拟得出锈蚀产物弹性模量方法是可行的.同时，也证实锈蚀产物微观结构更可能是由4种物质非均匀混合形成的.图7为钢筋锈蚀产物试样B的SEM照片.由图7可见，钢筋锈蚀产物分布不均匀，也验证了修正模型的正确性.

3 结论

(1)利用分子动力学软件Lammps模拟了纳米压痕试验，通过荷载-位移曲线得到锈蚀产物试样A和B的弹性模量值，分别为160.9、163.3GPa，与已有文献结果较为吻合，验证了本模拟方法的可行性.

(2)将层层均匀叠加模型与非均匀混合模型进行对比，发现非均匀混合模型结果与实际更加吻合，说明钢筋锈蚀产物的微观模型是4种锈蚀物质非均匀混合而形成的.

(3)基于分子动力学的纳米压痕模拟方法，能够有效避免因试验方法和环境不同所带来的结果差异，可作为一种测量钢筋锈蚀产物弹性模量的新手段.