基于L2范数实际重要性的MEWMA在线控制图*
廖玉琼,訾雪旻
(天津职业技术师范大学理学院,天津 300222)
1 问题描述
生产过程中需要对各个阶段进行评估和监控,实现对过程质量有效评价的同时尽早发现异常,并给出预警信号.Shewhart[1]首先提出了用于生产过程监控的控制图.这种质量控制技术已在世界范围内推广应用.但Shewhart控制图对中、小漂移始终不能达到很好的监控效果,Roberts[2]于1959年提出指数加权移动平均(EWMA)控制图.在大规模生产中,影响过程质量的许多变量往往是相互关联的.Lowry[3](1992)提出的多元指数加权移动平均(MEWMA)控制图可用于同时监测多个相关过程变量,Runger与Prabhu(1997)[4],Michael(2008)[5]和Zou(2013)[6]等人讨论了关于这一主题的大量文献.上述介绍的方法都依赖于经典假设检验,而在实践中,并不需要尽快检测到这些微小的偏差.如Box等人(2003~2004)指出,“被监测的系统(工厂)要么是‘好的’要么是‘坏的’的想法过于简单化.”在这样的情况下,Dett[8](2016)研究了带有可容许度的检验问题,克服了标准假设检验带来的不足.在Woodall[9](2013)重新思考控制图的文章中,可以找到文献综述,描述了如何使控制图具有实际重要性,而不仅仅是统计重要性.这种想法并不完全是新的,但有关于此的在线监控问题,迄今还没有被讨论.本文将结合实际情况,提出一种基于L2范数和具有可容许度的MEWMA在线控制图,来监控具有实际重要性的变化.通过模拟研究,说明应用该MEWMA控制图能有效降低在监控过程中的误报发生次数,提高在线监控效率.
2 MEWMA控制图
在MEWMA控制图中,假设Xi=(Xi1,Xi2,…,Xip)T,(i=1,2,…,)是从监控过程中选取的p维相关质量特征的第i个测量值,其中Xij是第j个特征的第i个测量值(j=1,2,…,p).假设Xi相互独立,且服从p维正态分布,即Xi~Np(μ0,Σ).其中μ0是可控状态下质量特征的均值向量;Σ为可控状态下质量特征的协方差矩阵.则MEWMA控制图的加权值Zi为:
Zi=RXi+(I-R)Zi-1
(1)
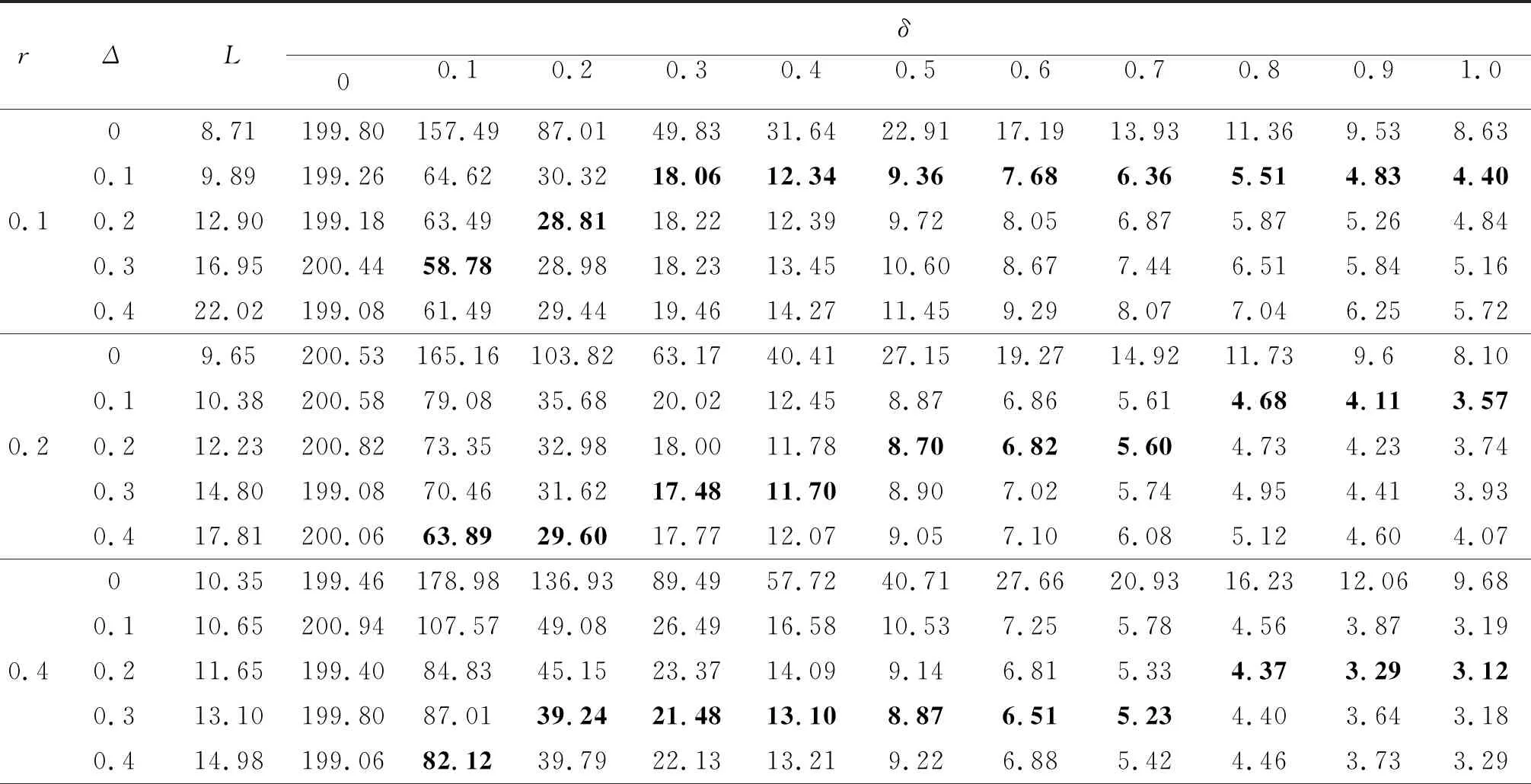
式中Z0=0(零矢量),I是单位矩阵且R=diag(r1,r2,…,rp),0 r1=r2=…=rp=r.此时,加权值Zi可以简化成: Zi=rXi+(1-r)Zi-1 (2) 当过程发生漂移μ时,非中心参数为: δ=(μ-μ0)TΣ-1(μ-μ0) (3) MEWMA控制图的控制统计量为: (4) 当Qi>H时,MEWMA控制图给出一个失控信号.其中H(>0)是满足某一给定可控平均运行长度(ARL0)而选取的上控制限.ΣZi是Zi的协方差矩阵,也就是: ΣZi={r[1-(1-r)2i]/(2-r)}Σ (5) 一般采用其渐进形式(i→∞): ΣZi={r/(2-r)}Σ (6) H0∶μ=μ0↔H1∶μ≠μ0 (7) 假设一列Xi,i=1,2,…来自一生产过程中,则在线监控过程如下: (8) 式中μ≠μ0,τ为未知的正整数.如果原假设成立,则生产线工作正常,如果备择假设成立,则希望控制图尽早地检测出漂移的发生及其时间.然而,上述经典假设不具有实际重要性,经常容易发生错误报警.如果错误报警次数太多,则警报往往被忽略,监控将变得无效.在医院重症监护室中,需要连续监控血氧饱和度、心率、心脏电描记、血压、温度和液体状态等多个变量.以成人收缩血压为例,当患者测量值在区间(90,140)mmHg内,则患者正常,否则,监控设备会通知护理人员.而在实际情况中,可能由于患者的移动等人为因素导致传感器的失效,产生过于频繁的错误报警.这些报警不仅对患者和护理人员是一种困扰;它们还可能危及患者的安全和患者护理的有效性.引入可容许度的检验问题,可以解决标准假设检验带来的缺陷.我们不再是快速检测患者血压在区间(90,140)mmHg内的漂移,而是快速检测到超过165 mmHg或低于65 mmHg的漂移.因此,根据实际需要,我们设计出一类新的控制图.它既能保证有效的降低错误报警的发生,又能快速检测过程发生的重要变化.本文基于带有可容许度的假设: H0∶‖μ-μ0‖≤Δ↔H1∶‖μ-μ0‖>Δ (9) 其中初始值μ0通常取零矢量,μ为带有漂移的均值矢量,‖·‖表示参数空间上的范数,Δ(>0)是一个预先设定的常数,表示实际情况中能接受的“最大”变化. (10) 结合实际重要性和预先设定的ARL0,本文的目标是找到L,使得 (11) 式中E0表示接受可控状态下的期望,检测变化值‖δ‖≤Δ,则δ表示可控状态下的均值.考虑MEWMA控制图的典型示例,Lowry (1992年)中控制图的表现仅与非中心性参数δTΣ-1δ的函数有关.此外,我们通常需要在实际应用中根据使用的难易程度来选取范数.从学习理论的角度来说,L2范数可以防止过拟合,提升模型的泛化能力;从优化或者数值计算的角度来说,L2范数有助于处理条件数不好的情况下矩阵求逆很困难的问题.从而,本文将该范数取为标准的L2范数,希望找到L,使得 (12) 等同于解决失控情形下的: (13) 式中δ应该与特征向量的方向相同,该特征向量对应于Σ的最小特征值,用γ1表示.因此,当漂移为δ时,通过取δ=Δγ1,我们可以将其等价于MEWMA控制图在给定失控状态下的ARL,通过二分法重新调整找到L的过程. 表1 不同平滑参数r和可容许度Δ情况下的控制限L和平均运行长度ARL 表1中,在光滑参数r和漂移δ一定时,随着可容许度Δ的增大,MEWMA控制图的控制限L也逐渐增大.结果表明,带有可容许度(Δ>0)的MEWMA控制图监控效果优于不带有可容许度(Δ=0)的MEWMA控制图.而且,在考虑具有可容许度的情况下(Δ>0),对于每组固定的r和δ,都能找到一个Δ的最优值(用黑色加粗表示),它在所示的选择中提供了最小的ARL.以r=0.1,δ=0.1为例,当Δ=0.1,0.2,0.3,0.4,0.5时,对应的控制限逐渐增大,分别为8.71,9.89,12.90,16.95,22.02.其中,当Δ=0时,其OC ARL为157.49,当Δ=0.1,0.2,0.3,0.4时,其OC ARL 分别为64.62,63.49,58.78,61.49.从中发现带有可容许度的OC ARL都低于不带有可容许度的OC ARL,且Δ的最优值为0.3.验证了在r和δ一定时,具有实际重要性MEWMA控制图的有效性.对于所有固定的r和δ,都能得到相似的结论. 此外,本文给出了基于可容许度Δ的平滑参数r的可适应性的选择.可容许度Δ的最优值随着平滑参数r的增大而增大.由表1知,当平滑参数r=0.1时,发生中、小漂移δ=0.1,0.2,0.3的OC ARL分别为58.78、28.81和18.06,其最佳的可容许度Δ约为0.2;发生大漂移δ=0.4,0.6,0.8,1.0的OC ARL分别为12.34、7.68、5.51和4.40,其最佳的可容许度Δ约为0.1.同样地,当平滑参数r=0.2时,产生中、小漂移的最佳的可容许度Δ在[0.2,0.3]之间;其大漂移的最佳的可容许度Δ在[0.1,0.2]之间.当平滑参数r=0.4时,它的中、小漂移的最佳的可容许度Δ在[0.3,0.4]之间;其大漂移的最佳的可容许度Δ在[0.2,0.3]之间.可以表明随着r的增加,Δ的最优值也是逐渐增大的. 本文将数据实际重要性和MEWMA控制图相结合,克服了传统控制图对漂移过分灵敏的缺点.研究发现,可容许度Δ的最优值随着平滑参数r的增大而略微增大.据此给出了不同的漂移情况下 ,MEWMA 控制图参数选择的小范围建议,对于进一步提升 MEWMA控制图的监控表现具有一定的指导意义.今后将对基于L2范数实际重要性的研究拓展到累积和(CUSUM)等其他控制图.3 实际重要性
4 基于L2范数实际重要性的MEWMA控制图
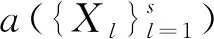
5 模拟研究
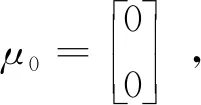
6 结论

