有轨电车扣配件式轨道结构铺设工期仿真

刘俊，狄怡霏，董成周，王卫东

有轨电车扣配件式轨道结构铺设工期仿真

刘俊1, 3，狄怡霏2，董成周2，王卫东1, 3

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 中铁十四局集团 第五工程公司，山东 济宁 272117；3. 中南大学 重载铁路工程结构教育部重点实验室，湖南 长沙 410075)

有轨电车作为一种新型公交，以其节能环保、绿化铺装等特点在国内的发展十分迅速。结合BIM技术以及蒙特卡洛方法，对有轨电车扣配件式轨道结构铺设进行施工阶段工期仿真及施工管理信息化研究，以期促进BIM技术在有轨电车方面中的应用。研究结果表明：以蒙特卡洛方法模拟确定的各工序持续时间及总工期概率分布，可为控制总工期、编制施工组织设计提供依据；利用Revit建立附加工期信息的轨道结构模型，可以形象展示施工过程，为调整工程进度、解决施工难点提供依据；基于BIM的施工管理信息化系统可以促进工程信息集成和共享，推动BIM在有轨电车工程中的应用。

有轨电车；轨道结构；工程进度；BIM；蒙特卡洛

随着城市建设的快速发展以及在低碳经济下对城市交通景观的要求，有轨电车的发展与建设迎来了重要的时期。有轨电车建设工程具有规模大，建设周期长，施工空间狭窄，工期紧，相关专业多等特点[1]。所以，在项目开工建设前要编制合理有序的施工进度表，使施工资源得到合理配备，在最大程度上减少工程的成本。BIM不仅可以实现三维建模，还可加入时间形成4D模型，加入成本形成5D模型，对项目进行全面管理。引入BIM技术后可以实现项目全生命周期管理，减少施工错误，节约工程管理成本，加快施工的进度。基于BIM的工程信息管理方式，将建设工程管理全过程中的工程相关文档、照片、图纸等过程资料进行集中管理，使工程项目系统内部的资源实现协调一致，形成项目信息管理的信息流网络[2]。当前，BIM在轨道交通中的应用较广泛，但大多数是针对特定的工程内容。由于有轨电车建设项目的复杂性、专业性强，依据BIM模型进行设计和施工的方法还不够成熟，在建设工程全生命周期中应用BIM的突出作用尚需进一步的开发提高[3-4]。成都市有轨电车的无砟轨道整体道床结构型式分4种：1) 扣配件型式； 2) 预制轨道板型式；3) 承轨槽型式；4) 现浇钢槽型式。本文应用蒙特卡洛的方法和BIM技术对有轨电车扣配件式轨道结构铺设进度进行仿真研究，研究整体结构框架如图1。依照扣配件式轨道结构的施工组织设计，确定每道工序。在施工现场，以50 m长度的轨道铺设为一个单元，首先调查每道工序的持续时间，取多组样本数据，拟合每道工序持续时间的概率分布函数和对应的参数。然后，根据施工网络计划图，以蒙特卡洛对每道工序持续时间进行100万次的试验模拟，得到有轨电车扣配件式轨道结构铺设总工期的概率分布。最后，建立扣配件式轨道结构BIM模型，直观展现仿真模拟结果，提高工程管理效率。

1 有轨电车扣配件式轨道结构铺设工作分解

基于WBS将研究对象进行工作分解，明确各工作之间前后逻辑关系。

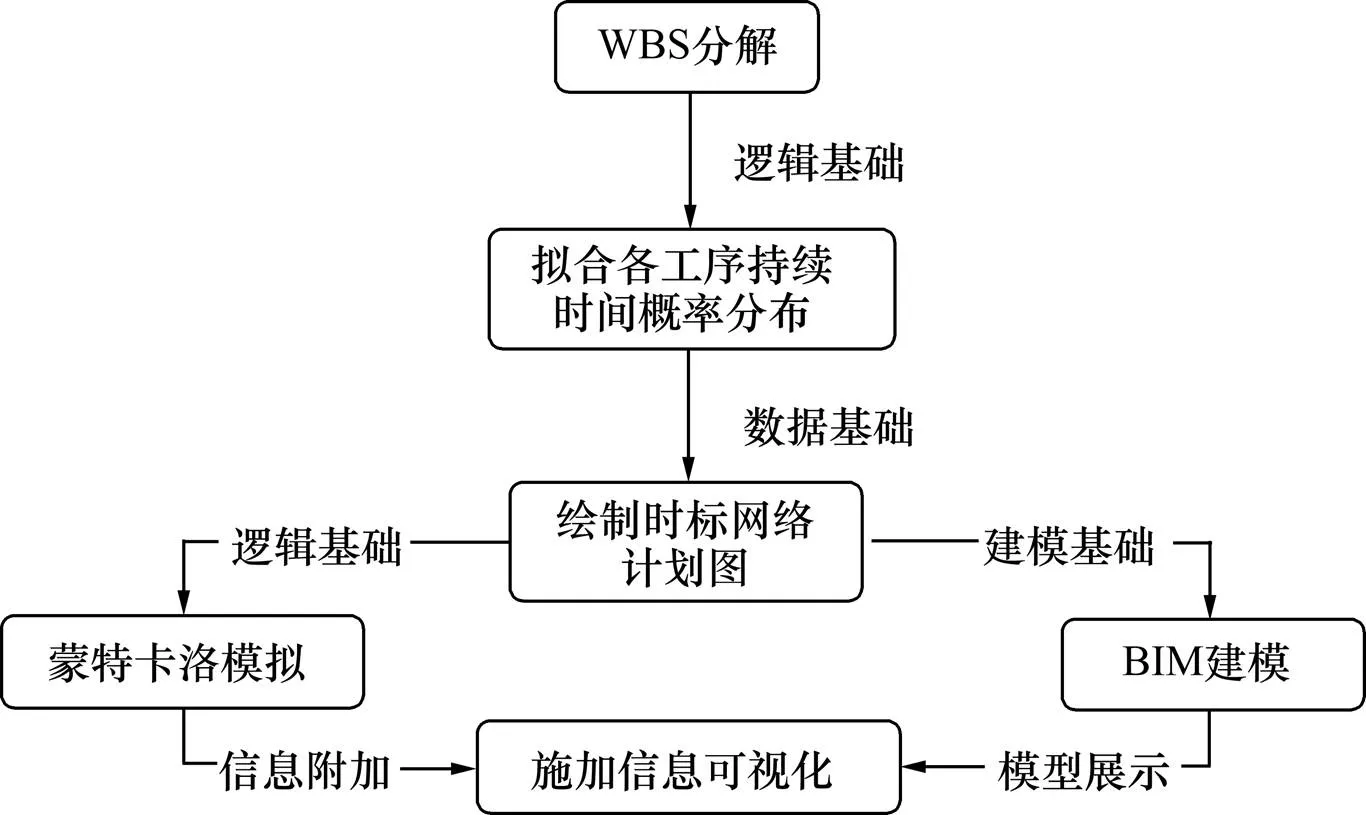
图1 研究框架

有轨电车扣配件式轨道结构的施工步骤多，需要制定细致的施工组织计划，逐层逐步地对施工过程进行工作分解，保证轨道结构建设满足规范要求。在详细调研成都有轨电车扣配件式轨道结构的铺设现场后，本文基于WBS法将扣配件式轨道结构铺设流程分解成了11道工序，如图2。

2 有轨电车扣配件式轨道结构铺设工法的网络计划图

2.1 双代号时标网络计划图

横道图及网络计划图是2种常用的工程进度计划表示方法。其中，横道图是传统方法，简单且应用范围较广，但对于大型工程，不能清晰表达各工序之间内在逻辑关系，也不能够明确整个进度计划的关键工作和路径。双代号时标网络计划图具备横道图和网络计划图的优势，一方面可以完整、清晰反映各工序间内在逻辑关系，另一方面又可以明确显示进度计划。本文采用双代号时标网络计划图表示施工网络计划。

图2 扣配件式轨道结构铺设施工流程

2.2 计划评审技术

对各工序之间逻辑关系和工序持续时间的研究，总体上经过了由确定到不确定2个过程。关键线路法(CPM)，各工序彼此之间逻辑关系和工序持续时间都认为是确定的，即各工序持续时间是常量[5−6]，工程总工期是关键路径中所有关键工序持续时间的总和。但是在工程施工中，各工序持续时间受各种人为、气象等因素的影响，并非常量，而是在一个时间范围内变动，使工程建设的关键线路发生变化，导致应用关键线路法计算的总工期不能准确反映实际状况。计划评审技术(PERT)假定各工序之间的逻辑关系确定但持续时间不确定，它假设各工序持续时间满足一种概率分布，采用三点估算法计算期望值作为各工序持续时间，以此反映工序持续时间的“不确定性”[7−9]。

本文以计划评审技术为基础，以蒙特卡洛模拟的试验方式，对工程进度进行概率统计分析，各工序持续时间期望值采用现场收集数据的均值。

2.3 扣配件式轨道结构铺设网络计划图

在工地现场确定的人员、机械、材料等条件下，对每道工序收集24组持续时间数据，确定工序持续时间的可能范围(如表1)绘制双代号时标网络计划图(如图3)。

表1 工作明细

图3 轨道铺设工程双代号时标网络计划图

3 蒙特卡洛模拟轨道结构铺设工期

蒙特卡洛方法，又称随机抽样方法，以大量试验数据为基础，确定目标变量值的一种数值计算方法[10−13]。本文根据施工现场的收集数据，拟合各工序持续时间的概率分布类型和相关参数，利用蒙特卡洛方法并结合PERT进行试验模拟，得到50 m长度单元的扣配件式轨道结构铺设总工期概率分布(图4)。

3.1 工序持续时间的数学分布

工序持续时间往往与现场工程资源配备(机械、人工、材料等)相关，轨道铺设要求的材料和机械配备基本相同，50 m长度单元的轨道铺设，配备人员：1) 测量放线人员配备：测量画点2人，放模板定位线2人；2) 轨排组装人员配备：散轨枕、扣件安装8人；3) 精调支架安装人员配备：支架安装6人；4) 轨道粗调人员配备：轨道粗调4人；5) 道床钢筋绑扎人员配备：绑扎钢筋8人，焊接钢筋3人；6) 伸缩缝施工人员配备：泡沫板安装2人；7) 模板安装人员配备：模板运输2人，支架钻口2人，安装模板4人；8) 轨道精调人员配备：操作全站仪1人，操作精调小车2人，轨道精调配合4人； 9) 混凝土浇筑人员配备：混凝土罐车驾驶员1人，泵车驾驶员1人，泵车指挥员1人，混凝土浇筑2人，平铺混凝土4人，混凝土收面6人，地面清洗2人；10) 混凝土养生人员配备：铺设土工布2人，浇水养护2人；11) 拆模人员配备：支架拆除4人，模板拆除4人。

对各工序持续时间的24组样本数据进行概率分布拟合，确定11道工序持续时间概率分布如表2，主要是Beta分布、均匀分布、负二项分布等，相较常用的概率分布函数拟合工程数据精度提高[14−15]。

表2 各工序持续时间概率分布类型及参数

3.2 蒙特卡洛模拟

根据各工序持续时间的拟合分布函数和双代号时标网络计划图，对50 m长度单元的轨道铺设过程，在既准确模拟又减少模拟耗费时间的条件下，以蒙特卡洛方法仿真模拟100万次，得到100万个工序持续时间和总工期试验结果，说明如下：

1) 总工期概率分布如图4。50 m长度单元的扣配件式轨道结构铺设总工期符合Gamma分布，分布参数为min=996.9，=215.3，=50.4。

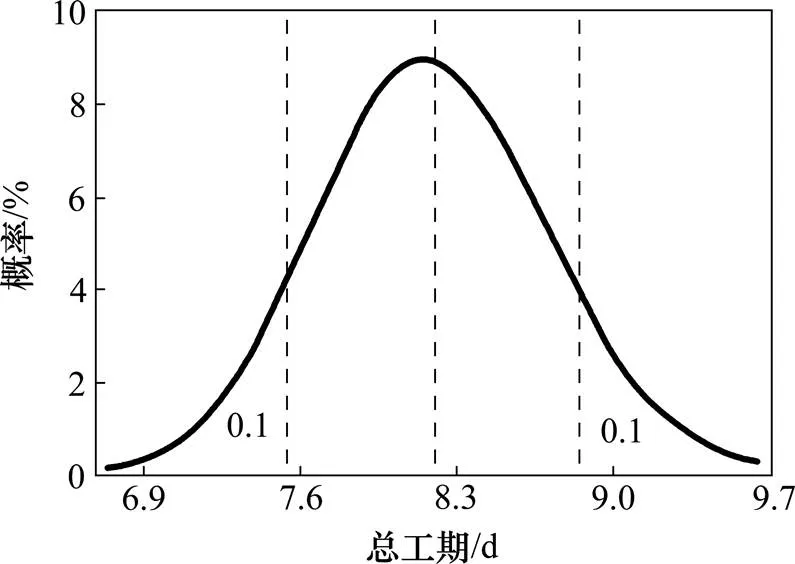
图4 总工期概率分布

2) 总工期的累计概率分布模拟结果如图5。可见，50 m长度单元的轨道铺设在8.9 d内完成的概率是90%。

图5 总工期累计概率分布

4 基于BIM的仿真系统

利用Revit建立有轨电车扣配件式轨道结构BIM模型，以工期为时间轴，根据双代号时标网络计划图，对轨道结构铺设过程进行4D动态展示，实现了有轨电车扣配件式轨道结构铺设进度的可视化管理。

4.1 扣配件式轨道结构3D模型

对应有轨电车扣配件式轨道结构铺设施工流程，建立底座板族、支撑块族、钢轨族共3个主要基础构件的参数化族，最后将各族组合成扣配件式轨道结构整体模型，如图6所示。

(a) 底座板族；(b) 支撑块族；(c) 钢轨族；(d) 整体三维模型

4.2 4D模型

将经过上述模拟试验确定的各道工序所需要的时间、轨道铺设总工期等信息附加于各构件，以工期为时间轴，依据双代号时标网络计划图，模拟工程施工进度，可动态展示轨道结构的建设过程。

系统(如图7)可输入实际工程进度，与计划进度对比，能及早的发现工期滞后问题，及时调整现场施工人员、工程材料、施工机械的配比，保证计划工期；为合理有序安排工程资源提供一定决策依据，避免出现工程资源闲置或紧张等问题。

建立工程信息管理系统(图8)，对施工过程中的相关资料进行集成和共享，为工程的进一步信息化、可视化提供基础。

图7 轨道结构铺设进度4D模拟

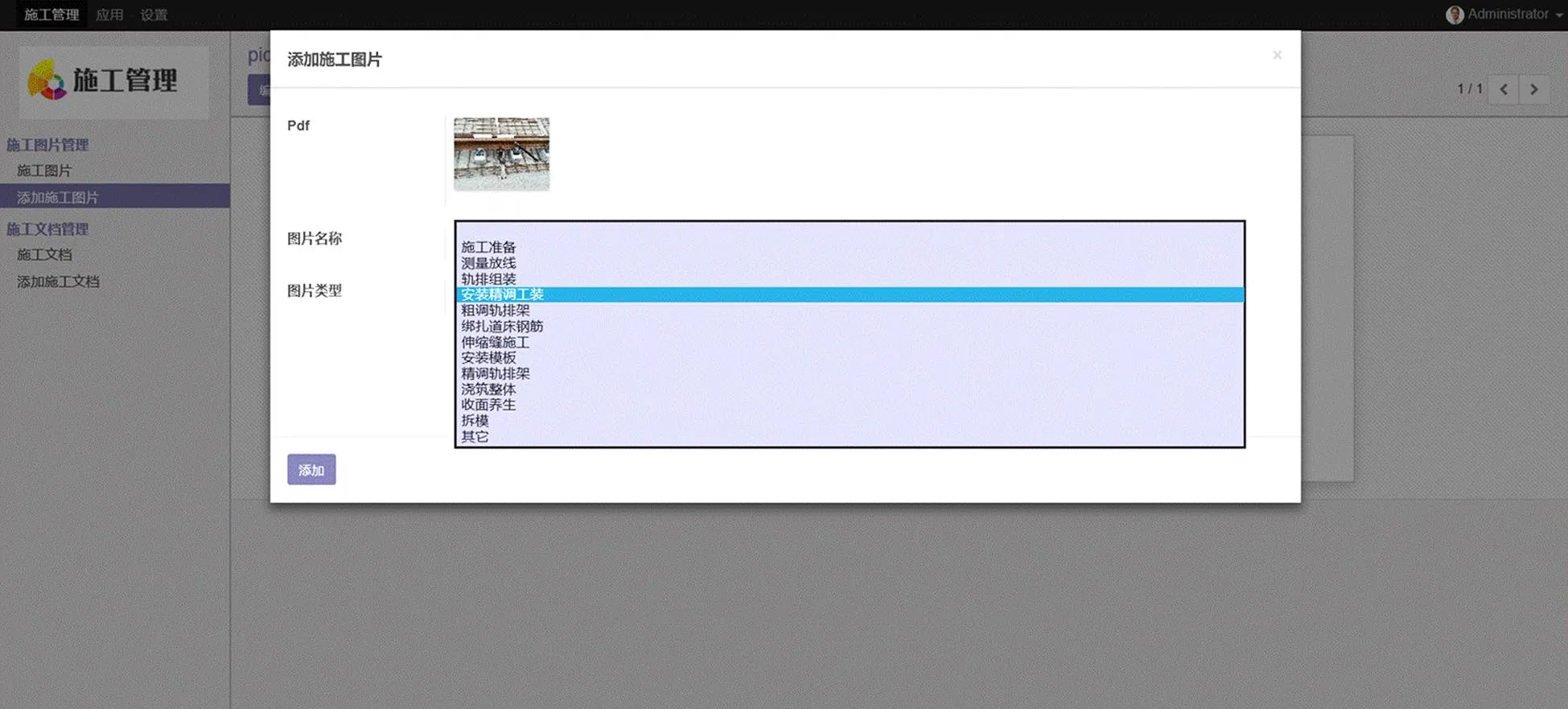
图8 工程信息管理系统界面

5 结论

1) 在一定的资源配置条件下，每道工序采集24组持续时间数据，分别确定11道工序持续时间的概率分布类型及参数。

2) 用蒙特卡洛方法模拟确定了50 m长度单元的有轨电车扣配件式轨道铺设总工期服从Gamma分布，在8.9 d内完成的概率为90%。

3) 建立了工程4D模型和工程信息管理系统，对合理安排工程进度或根据工程进度合理配置工程资源提供了可视化平台。

[1] 傅明华, 余洋. BIM和信息技术在有轨电车中的探索和应用前景[J]. 上海建设科技, 2017(2): 11−15. FU Minghua, YU Yang. Exploration and application prospects of BIM and information technology in trams[J]. Shanghai Construction Science and Technology, 2017(2): 11−15.

[2] 奚栋梁. BIM和信息技术在有轨电车中的应用[J]. 科学与信息化, 2017(14): 21−22. XI Dongliang. Application of BIM and information technology in trams[J]. Science and Information Technology, 2017(14): 21−22.

[3] 段熙宾. 大型铁路工程BIM设计的探索及实现[J]. 铁道标准设计, 2016, 60(12): 124−127. DUAN Xibin. Exploration and realization of BIM design of large-scale railway engineering[J]. Railway Standard Design, 2016, 60(12): 124−127.

[4] 夏宇, 谭衢霖, 蔡小培, 等. 铁路BIM应用三维线路场景构建研究[J]. 铁路计算机应用, 2018, 27(7): 95−98. XIA Yu, TAN Qulin, CAI Xiaopei, et al. Railway BIM applied to 3D line scene construction[J]. Railway Computer Application, 2018, 27(7): 95−98.

[5] 谢志强, 韩英杰, 齐永红, 等. 基于关键路径和任务复制的多核调度算法[J]. 国防科技大学学报, 2014, 29(1): 172−177. XIE Zhiqiang, HAN Yingjie, QI Yonghong, et al. A scheduling algorithm for multi-core based on critical path and task duplication[J]. Journal of National University of Defense Technology, 2014, 29(1): 172−177.

[6] Kelley J E, Walker M R. Critical path planning and scheduling[C]// Proceedings of the Eastern Joint Computer Conference. Boston, USA, 1959: 160−173.

[7] Clark C E. The PERT model for the distribution of an activity time[J]. Operations Research, 1962, 10(3): 405− 406.

[8] Hahn E D. Mixture densities for project management activity times: A robust approach to PERT[J]. European Journal of Operational Research, 2008, 188(2): 450−459.

[9] Malcolm D G, Roseboom J H, Clark C E, et al. Application of technique for a research and development program evaluation[J]. Operations Research, 1959, 7(5): 646−669.

[10] 郭琦, 何金静, 胡苗. 基于蒙特卡洛模拟的工程项目网络计划进度风险分析[J]. 项目管理技术, 2013, 11(11): 66−70.GUO Qi, HE Jinjing, HU Miao.Strategic analysis of network planning progress based on Monte Carlo simulation[J]. Project Management Technology, 2013, 11(11): 66−70.

[11] 邵伟.蒙特卡洛方法及在一些统计模型中的应用[D]. 济南: 山东大学, 2012.SHAOWei.Monte Carlo methods and their applications in some statistical model[D]. Jinan: Shandong University, 2012.

[12] 王霞, 张本涛, 马庆. 蒙特卡洛法在投资项目风险分析中的应用[J]. 价值工程, 2011(26): 64−65. WANG Xia, ZHANG Bentao, MA Qing. Analysis of investment risk based on Monte Carlo method[J]. Value Engineering, 2011(26): 64−65.

[13] 罗丽哲, 胡志根, 刘全, 等. 高坝施工全过程导流风险多维评估[J]. 中南大学学报(自然科学版), 2014, 45(3): 840−846. LUO Lizhe, HU Zhigen, LIU Quan, et al. Multi- dimensional estimation for risk of diversion system in high-dam construction process[J]. Journal of Central South University (Science and Technology), 2014, 45(3): 840−846.

[14] 徐志军, 张博, 王凯, 等.基于Beta分布的改进的一次可靠度法研究[J].土木工程与管理学报, 2014, 31(3): 17−21. XU Zhijun, ZHANG Bo, WANG Kai, et al.Study of modified first order reliability method on Beta distribution[J]. Journal of Civil Engineering and Management, 2014, 31(3): 17−21.

[15] 刘银萍. 均匀分布的相关性质以及检验[D]. 扬州: 扬州大学, 2016: 1−35. LIU Yinping. Uniform distribution of the correlation properties and testing[D]. Yangzhou: Yangzhou University, 2016: 1−35.

Period-simulation of tram buckle-type track structure

LIU Jun1, 3, DI Yifei2, DONG Chengzhou2, WANG Weidong1, 3

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. Fifth Engineering Company, China Railway fourteen Bureau Group, Jining 272117, China;3. Key Laboratory of Engineering Structures of Heavy Haul Railway of Ministry of Education, Central South University, Changsha 410075, China)

Trams, as a new type of bus, have developed rapidly in China due to their energy saving, environmental protection and green paving. This paper combined BIM technology and Monte Carlo method to carry out period-simulation in construction and informatization of construction management of tram buckle-type track structure laying in order to promote the application of BIM technology in trams. The research results are as follows: The duration of each process and the probability distribution of the total construction period are determined by Monte Carlo simulation, which provides a basis for controlling the total construction period and preparing the construction organization design; Use Revit to build a track structure model with additional construction time information, which can visually show the construction process, and provide a basis for adjusting the progress of the project and solving construction difficulties; The BIM-based construction management information system can facilitate the integration and sharing of engineering information, and promote the application of BIM in tram projects.

tram; track structure; project progress; BIM; Monte Carlo

[U239]

A

1672 − 7029(2020)12 − 3045 − 07

10.19713/j.cnki.43−1423/u.T20200135

2020−02−21

中铁十四局有轨电车轨道工程关键技术开发研究项目(YGDC-30)；教育部人文社会科学研究项目(13YJA630091)

王卫东(1971−)，男，江西上饶人，教授，博士，从事道路与铁道工程研究；E−mail：147745@163.com

(编辑 涂鹏)