全封闭声屏障断面尺寸对列车风压荷载影响规律的数值模拟

杨斌，马西章，郭柯桢，何旭辉, 4，敬海泉, 4

全封闭声屏障断面尺寸对列车风压荷载影响规律的数值模拟

杨斌1，马西章2，郭柯桢3，何旭辉3, 4，敬海泉3, 4

(1. 中国国家铁路集团有限公司，北京 100844；2. 雄安高速铁路有限公司，河北 保定 071700；3. 中南大学 土木工程学院，湖南 长沙 410075；4. 高速铁路建造技术国家工程实验室，湖南 长沙 410075)

为研究由列车高速通过全封闭声屏障时诱发的气动效应，探究断面面积对声屏障风压荷载的影响，基于计算流体力学软件FLUENT，以某时速350 km/h高速铁路全封闭声屏障为研究对象，对高速列车通过不同净空面积的全封闭声屏障过程进行数值模拟，分别从气压波传播规律、声屏障气动荷载变化规律以及典型截面各测点压力分布3个方面开展研究。模拟结果验证了声屏障内气压波的传播规律与隧道结构类似，获得了全封闭声屏障气动压力极值随断面面积变化的关系曲线，发现同一截面风压在环向存在明显不对称分布。本文研究成果可为全封闭式声屏障结构设计提供理论依据。

全封闭声屏障；350 km/h；断面尺寸；数值模拟；气动压力分布

近年来，高速铁路350 km/h的运营速度正在成为主流，极大地方便了人们的日常出行，提高了生活质量和工作效率。但随着人们环保意识的提升，高铁噪声对沿线自然环境及居民生产生活的影响也越来越受到重视。尤其是当高铁线路穿越噪声敏感区域时，必须采取相应措施对其产生的噪声进行控制。声屏障是控制噪声的重要措施之一[1]，可以显著降低噪声的传播范围和强度。目前，高速铁路声屏障根据不同的降噪标准和工程需求呈现出多种结构形式[2]，其中全封闭式声屏障因其出色的降噪效果而广泛应用于对声环境要求较为严苛的环境中。全封闭声屏障能够大幅降低环境噪声污染的同时，因其形成相对封闭的空间，限制了其内部气流的流通路径，导致高速列车通过声屏障时在内部产生较大的风压荷载，对声屏障结构安全构成威胁[3]。目前，针对全封闭声屏障列车风荷载的研究十分稀少，结构设计过程中主要参考隧道空气动力学的研究成果。隧道空气动力学作为列车空气动力学的一个分支，已经取得了较多的研究成果。例如：CHEN等[4]通过模拟350 km/h高速列车通过典型的双线隧道，讨论了头车变化段长度对隧道壁面气动荷载的影响；NIU等[5]通过三维数值模拟的方法，研究了列车长度与隧道表面的压力波波形、压力幅值及分布规律的影响；ZHANG等[6]选用RNG−湍流模型，模拟了高速列车进入隧道时的脉动风压分布，并探讨了隧道入口斜率对列车表面脉动风压的影响。韩珈琪等[7]利用数值模拟中的动态铺层技术，模拟了作用在声屏障上的脉动风压特性，并对不同形式声屏障的气动特性进行了讨论；李志伟等[8]对两单线隧道之间的横通道缓解隧道内瞬变压力的影响进行了数值模拟,得到了当高速列车通过有无横通道的隧道时隧道壁面及车体表面测点的瞬变压力时间历程及其变化幅值；王英学等[9]同样使用数值模拟方法对高速列车进入有间缝式开口缓冲结构的隧道的空气动力学特性进行三维数值模拟，并且分析间缝式单、双开口缓冲结构的最优结构形式；骆建军等[10]和研究了隧道横通道以及入口缓冲结构对气压波的影响规律；马辉等[11−12]分别研究了隧道断面尺寸对于气压波大小以及车内顺便压力的影响。高速铁路全封闭声屏障结构形状与隧道结构类似，既有隧道空气动力学的研究成果对全封闭声屏障列车风压荷载具有一定参考意义；然而，由于声屏障质量更轻、结构更柔，因此对列车风荷载更加敏感，既有隧道空气动力学研究成果无法满足全封闭声屏障结构设计要求；目前针对高速铁路列车风导致全封闭声屏障气压压力分布的研究十分稀少。因此，本文以我国某高铁线路840 m全封闭式声屏障为研究背景，采用数值模拟方法，按照实车模型和实际运行速度建立流固耦合模型；详细研究了声屏障截面尺寸对声屏障壁面风压荷载的影响规律。研究成果可为今后全封闭式声屏障的结构设计提供理论依据。

1 数值计算模型及测点布置

1.1 计算模型

综合考虑计算效率与计算精度，本文对列车模型进行了适当简化，如图1所示，忽略了转向架、车门、受电弓等结构，并对列车表面进行光滑处理。为了更加真实模拟实际情况，采用该线路常用的CRH380A型列车，并选择8列编组建立模型。

图1 CRH380A型列车模型示意图

该全封闭声屏障位于桥梁上部，数值计算模型由立柱、横梁、纵向连接系、单元板等组成，为了提高计算效率，模型表面进行了平滑处理，弧形面板的半径为3.45 m，弧顶距底部13.6 m，桥面板宽度为12.7 m。整体计算域分为3部分，如图2所示，中间部分包含声屏障，共840 m；为了使列车的加速过程更加充分，减小误差，参考既有文献并进行试算以后，在中间计算域的两端分别向两侧延伸550 m，分别为列车的加减速区域。同时，为了减小列车移动对边界条件造成影响，列车初始位置设置在距两侧边界200 m处，流域的宽度和高度都设置为50 m。

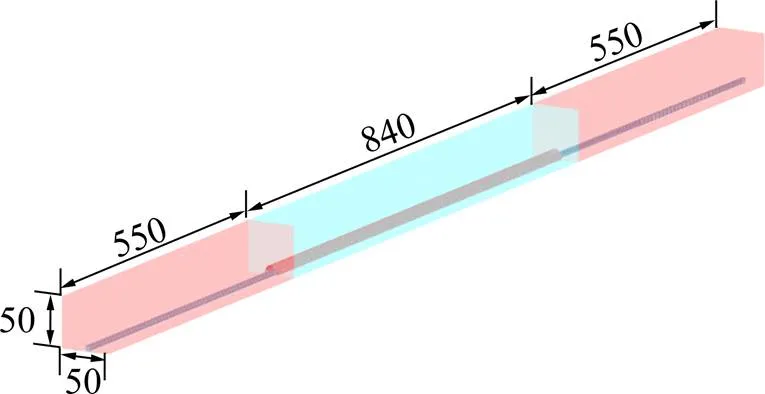
单位：m

为了实现列车在声屏障中的相对运动，采用动网格技术的动态铺层法，将列车及列车周围有限空间内的流体当作刚体，称之为移动网格区域，通过加载profile文件的方式定义其运动规律，实现与声屏障的相对运动，而包含声屏障在内的区域称之为静止网格区域，动网格区域和静网格区域之间通过interface交界面实现计算域之间的数据交换。图3为计算域边界条件设置示意图。计算域的侧面和顶面都采用压力出口边界，地面、列车以及声屏障设置为无滑移边界。

由于声屏障骨架是H型钢，结构外形较为复杂，计算模型采用非结构化网格。为了更详细地捕捉到结构附近的流体运动情况，提高模拟精度，在声屏障及靠近列车区域采用加密网格；而在远离结构物的外部区域采用稀疏网格，以便提高计算效率。经过一系列网格无关性试算之后，最终确定列车表面网格最大尺寸为0.2 m，声屏障表面网格最大尺寸为0.3 m，全局网格最大尺寸为1 m，总网格数为2 400万。

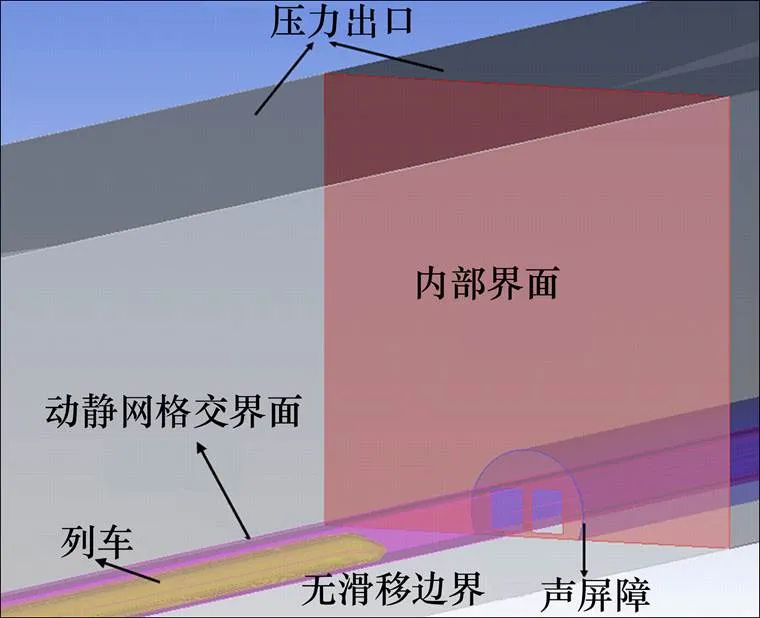
图3 计算边界条件设置示意图

本文基于RANS方法，根据已有文献结论[10]作为参考，选用准确、高效、适用性强的标准−两方程湍流模型，也是目前工程领域被广泛运用的流体计算模型之一。

1.2 测点布置

本次研究总共布置有11个风压监测截面，各截面位置由表1所示，依据由两端逐渐向中间加密的原则，在接近声屏障出入口的区域监测截面间隔100 m，在中间区域截面间隔10 m。每个监测截面上在声屏障内表面沿环向布置11个监测点，如图4所示。

表1 监测截面编号位置

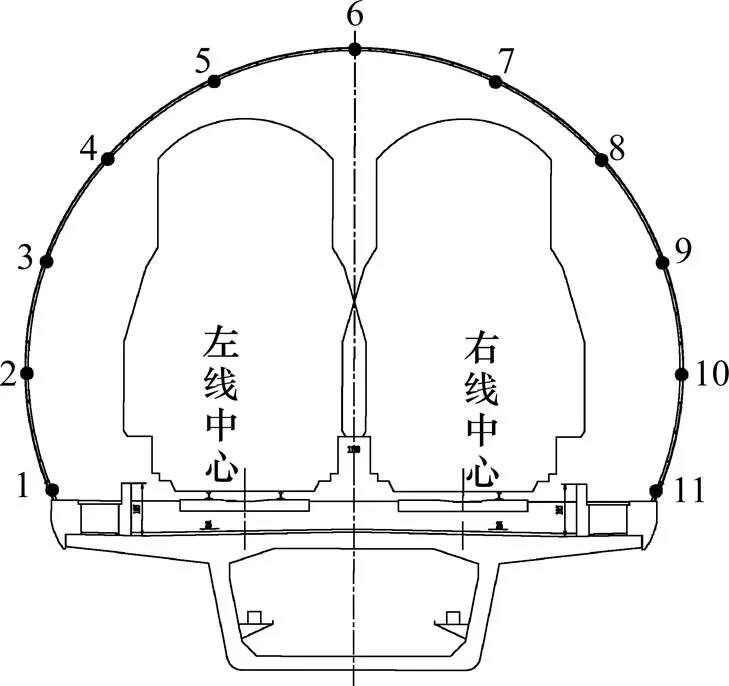
图4 截面测点分布示意图

2 模拟结果分析

2.1 压力波传播规律

图5(a)为单车通过该声屏障时气压波传递规律的示意图，图5(b)为单车以350 km/h经过断面尺寸110.5 m2声屏障时，中间测试截面的压力时程图。根据列车鼻尖、车尾进入声屏障时形成的压缩波、膨胀波(其中红线表示车头、车尾的行进过程)以及两者依据声速传播，并在洞口处以另一种波的形式返回的传递过程示意图，车头和车尾的经过也会引起相应位置的压力变化，红线表示两者随时间的移动位置。以中间截面为研究对象，，，，，和6个点分别表示压缩波(膨胀波)或者车头、车尾到达中间截面的时刻，其中压缩波到达时会使压力增加，膨胀波到达时会使压力减小，与已有文献[6]结论一致。

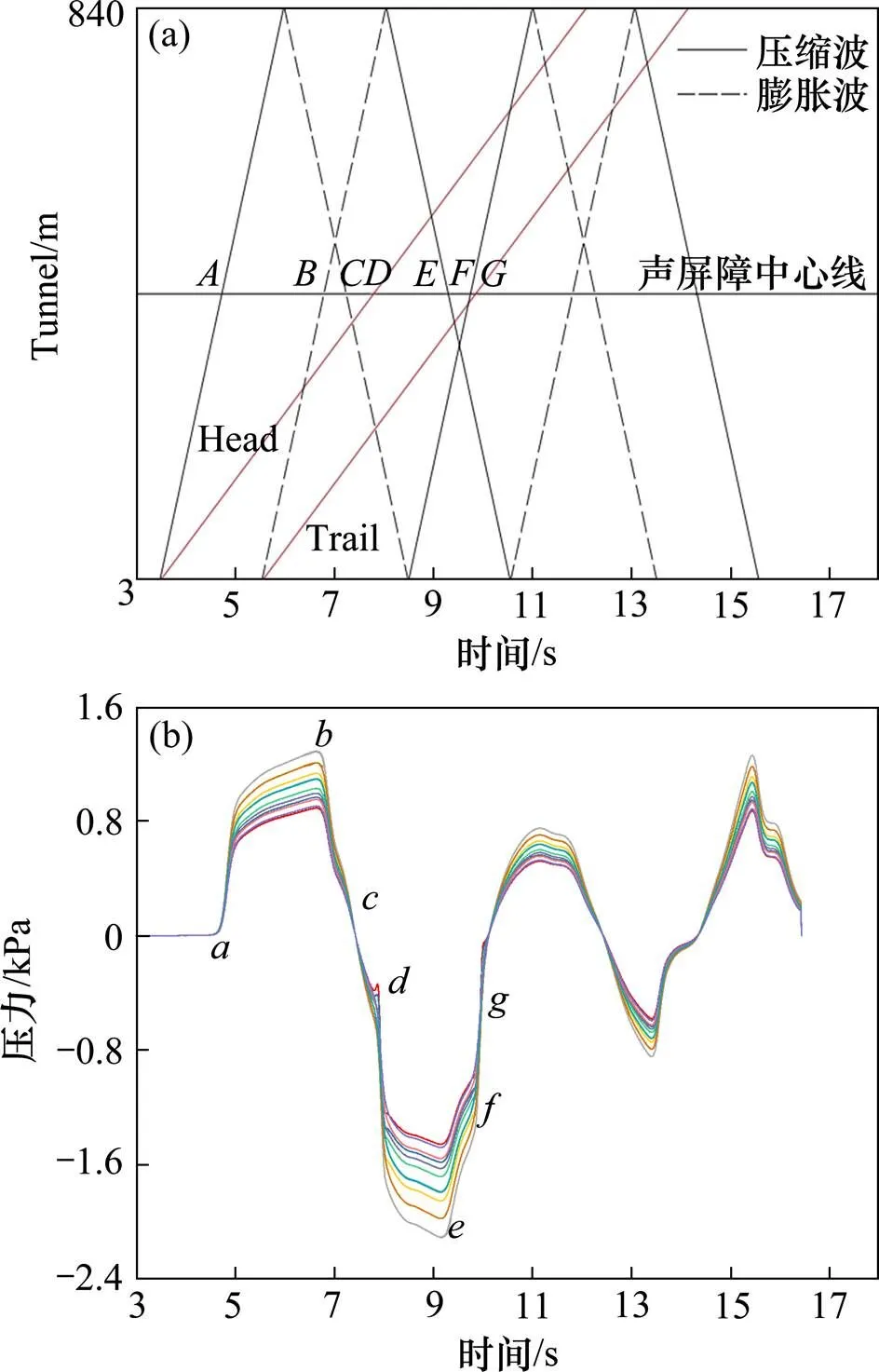
(a) Sketch Map 示意图；(b) Time history chart 时程图

点表示车头进入声屏障时产生的压缩波以声速到达中间截面处，对应下图点处压力的增加；点表示车尾进入声屏障时产生的膨胀波到达中间截面，对应于下图的点，即鼻尖处压力开始减小；点表示之前车头进入产生的压缩波经过传递到声屏障的出口反射回来的膨胀波再次经过中间截面，对应于下图的点，压力值继续减小；点表示车头经过中间截面处，对应于点也体现出测点压力的减小；和两点都是因为膨胀波的反射形成的压缩波经过中间截面，对应于和点压力值的增加；点表示车尾到达中间位置处，会引起所在位置测点压力值的增加，这与点的变化趋势一致。经过对比分析，其规律与中间截面测点的压力时程图变化一致，因此可以验证压力曲线的变化情况，以及解释气动压力波的传播规律[14]。

2.2 声屏障断面尺寸对气动荷载的影响

借鉴隧道空气动力学的研究经验采用阻塞比量化声屏障断面尺寸。阻塞比定义为列车横截面积与声屏障断面面积的比值。本文计算的3个声屏障断面，如表2所示，面积分别为121.6 m2，110.5 m2和99.5 m2，对应的阻塞比分别为1=9.6%，2=10.6%和3=11.8%。

表2 不同阻塞比工况

图6为列车以350 km/h的运行速度经过不同阻塞比的全封闭声屏障时，中间测试断面各测点的风压时程曲线。结果表明3种阻塞比下，截面气动荷载波动趋势基本一致，且都在6.6 s左右，即列车头部行驶至距声屏障入口312 m处，出现最大正压；都在9.1 s左右，即列车尾部经过中间截面，出现最大负压。最大正压和最大负压值都随着阻塞比的增加而增大。

图7为最大正压、最大负压以及最大压力幅值随阻塞比的变化情况，并且采用指数函数拟合阻塞比与极值风压的关系，结果表明最大正压、最大负压以及最大压力幅值随阻塞比的变化规律十分 一致。

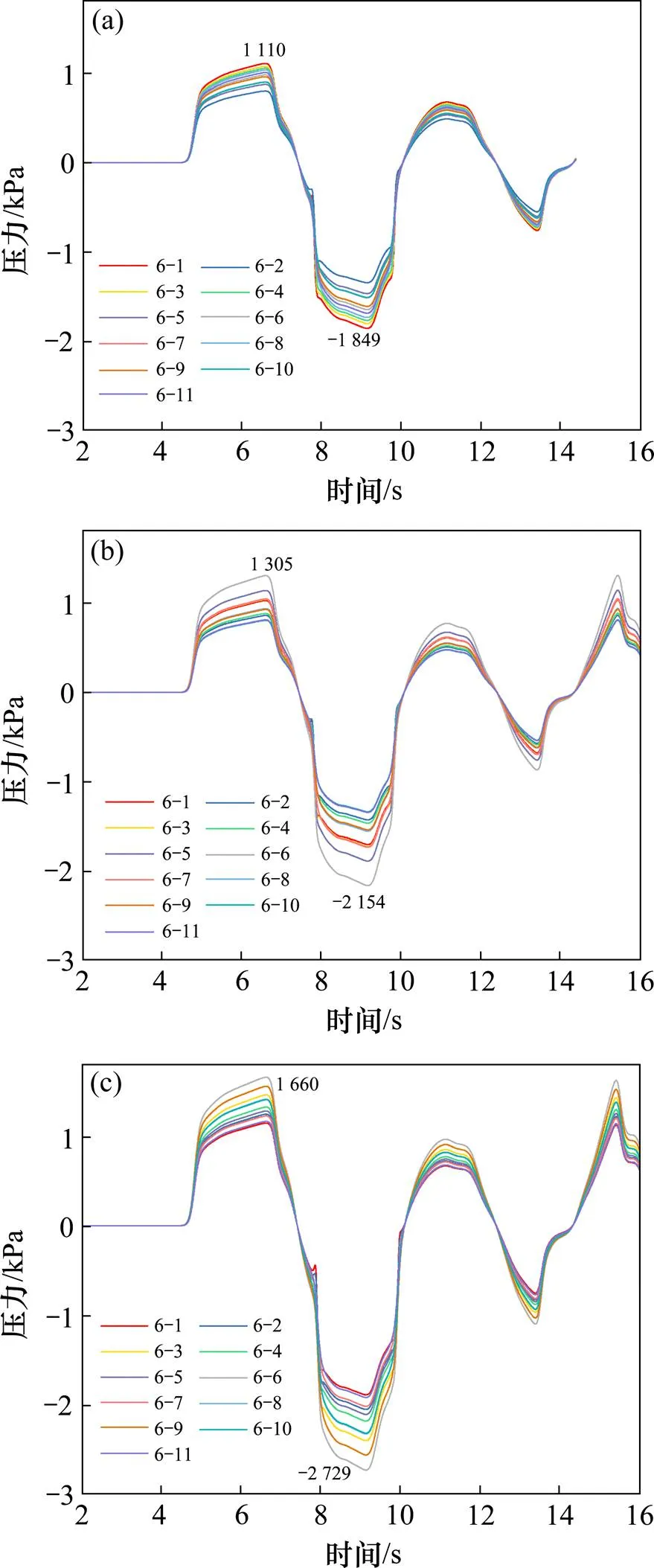
(a) R1；(b) R2；(c) R3

表3总结了3种阻塞比全封闭声屏障各个监测截面的最大正压、最大负压以及最大压力变化幅值。结果表明，3种阻塞比下风荷载均在中间截面取得极值，且沿两端逐渐降低，说明3种阻塞比下中间截面均为最不利截面。阻塞比1时最大正压为1 110 Pa，最大负压为−1 849 Pa，压力变化幅值为2 959 Pa；阻塞比2时最大正压为1 305 Pa，最大负压为−2 154 Pa，压力变化幅值为3 459 Pa；阻塞比3时最大正压为1 660 Pa，最大负压为−2 729 Pa，压力变化幅值为4 389 Pa。当阻塞比由1增加(面积减小)10%和20%时，各测试截面的正压力极值平均增大17.6%和49.5%，负风压极值平均增大16.5%和47.6%，最大压力变化幅值平均增大16.9%和48.3%。结果证明全封闭声屏障截面面积对于其自身的气动荷载影响显著，跟隧道空气动力学的研究结论一致[13]。

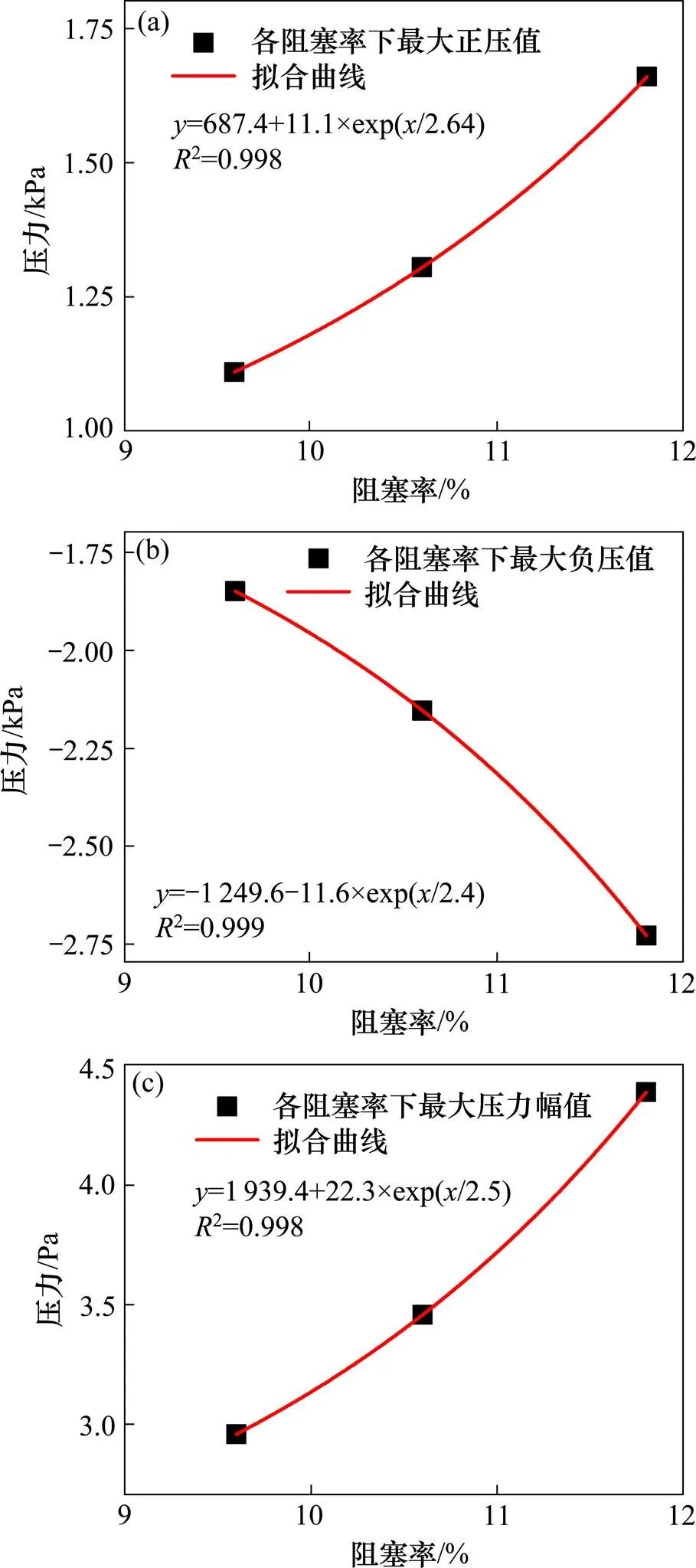
(a) 最大正压；(b) 最大负压；(c) 最大压力幅值

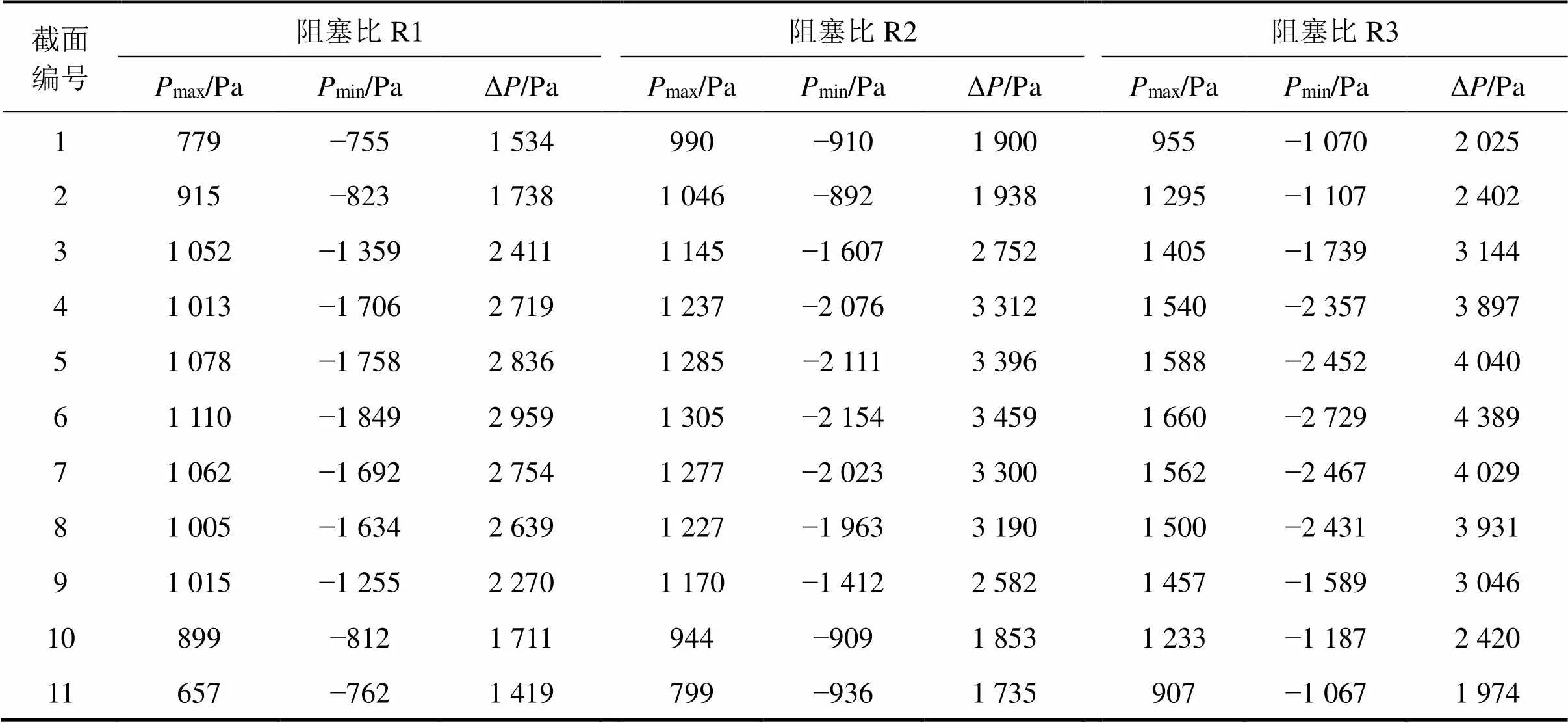
表3 各个阻塞比下声屏障壁面各项压力极值

图8为3种阻塞比工况下，各个监测截面的压力变化幅值与距离声屏障入口位置的关系曲线。随着阻塞比的增加，各个截面的压力变化幅值均增大；3种阻塞比下压力变化幅值均呈现出中间高两端低的变化规律，靠近声屏障出入口的截面压力变化幅值均小于中间区域的压力变化幅值，且对称截面的风压荷载基本遵循对称原则。

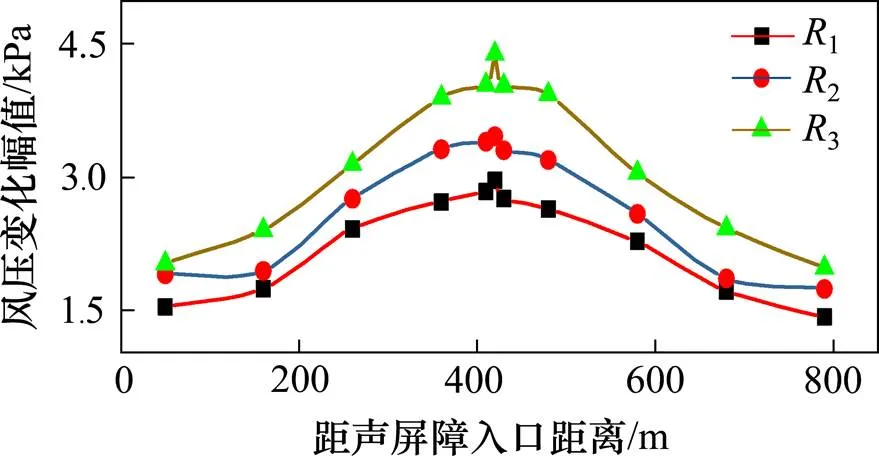
图8 不同阻塞比下各截面最大压力变化幅值

2.3 沿声屏障展向方向的气动荷载分布

图9为3种不同阻塞比下，距全封闭声屏障入口50 m的1号截面和距离全封闭声屏障入口410 m的中间截面，即6号截面的典型测点的风压时程图。结果显示，不同阻塞比下同一截面上的典型测点气动荷载波动趋势完全一致，但是风压值随着阻塞比的增大而增大，而且，中间截面的变化更显著。

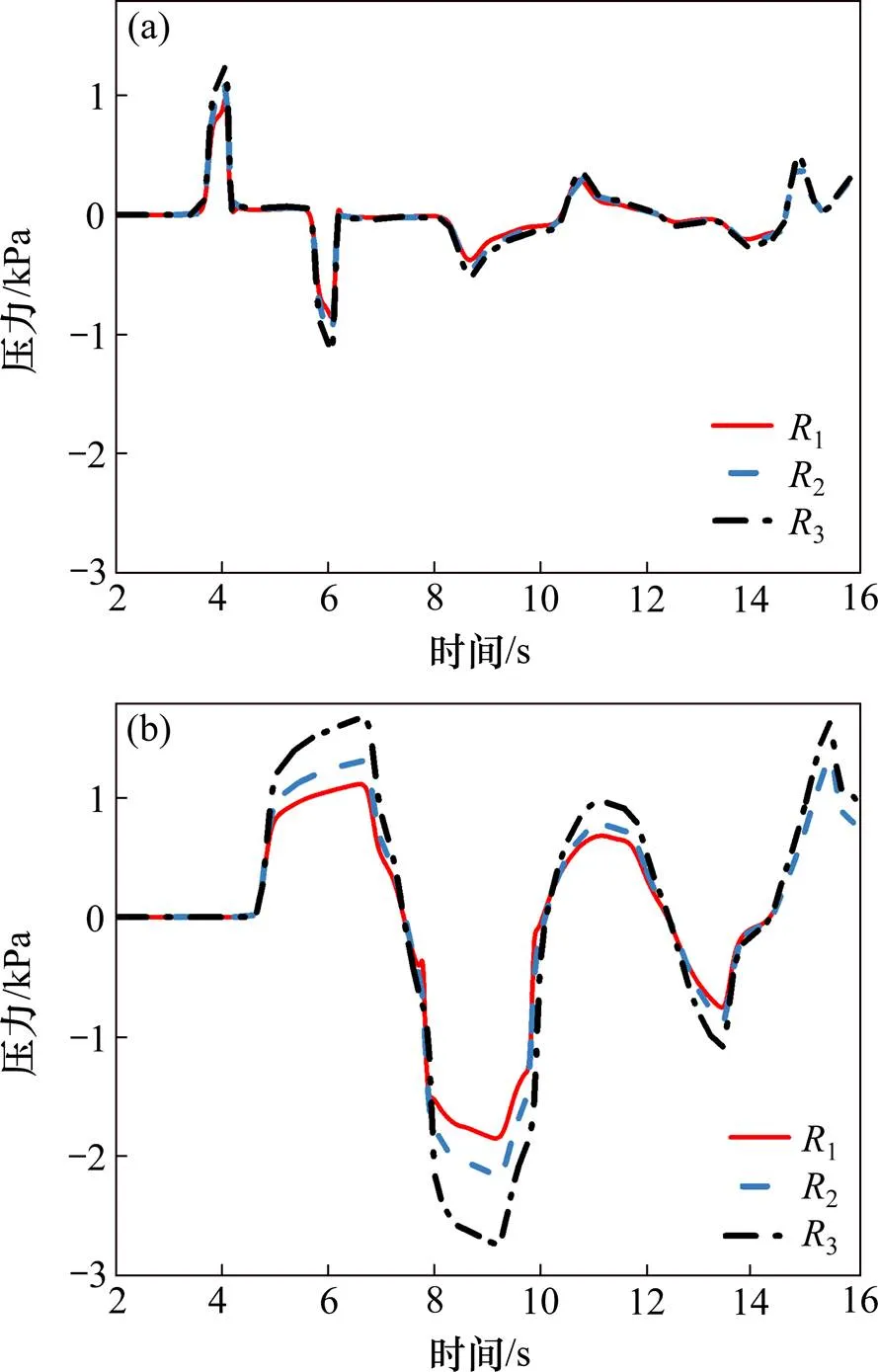
(a) 1号截面；(b) 6号截面

2.4 典型截面各测点的压力分布情况

图10为3种阻塞比下，压力极值最大截面即6号截面上出现最大正压和最大负压时刻，各测点的压力分布图。圧力曲线在全封闭声屏障外侧为正压、内侧为负压，设置声屏障外轮廓线为风压基准线，其风压取值为该截面各测点的最小值，以便凸显不同测点的差异。结果显示，同一截面上风压大小沿环向存在显著差异，阻塞比1工况下，最大正压差为32.5%，最大负压差为32.1%；阻塞比2工况下，最大正压差为45.0%，最大负压差为39.0%；阻塞比3工况下，最大正压差为33.9%，最大负压差为36.5%。3种阻塞比工况下，截面风压分布规律保持一致(即列车运行一侧的风压明显高于另一侧)，但是风压值随着阻塞比的增大而增大；由此说明声屏障阻塞比对截面风压环向分布规律影响较小，对风压值影响显著。

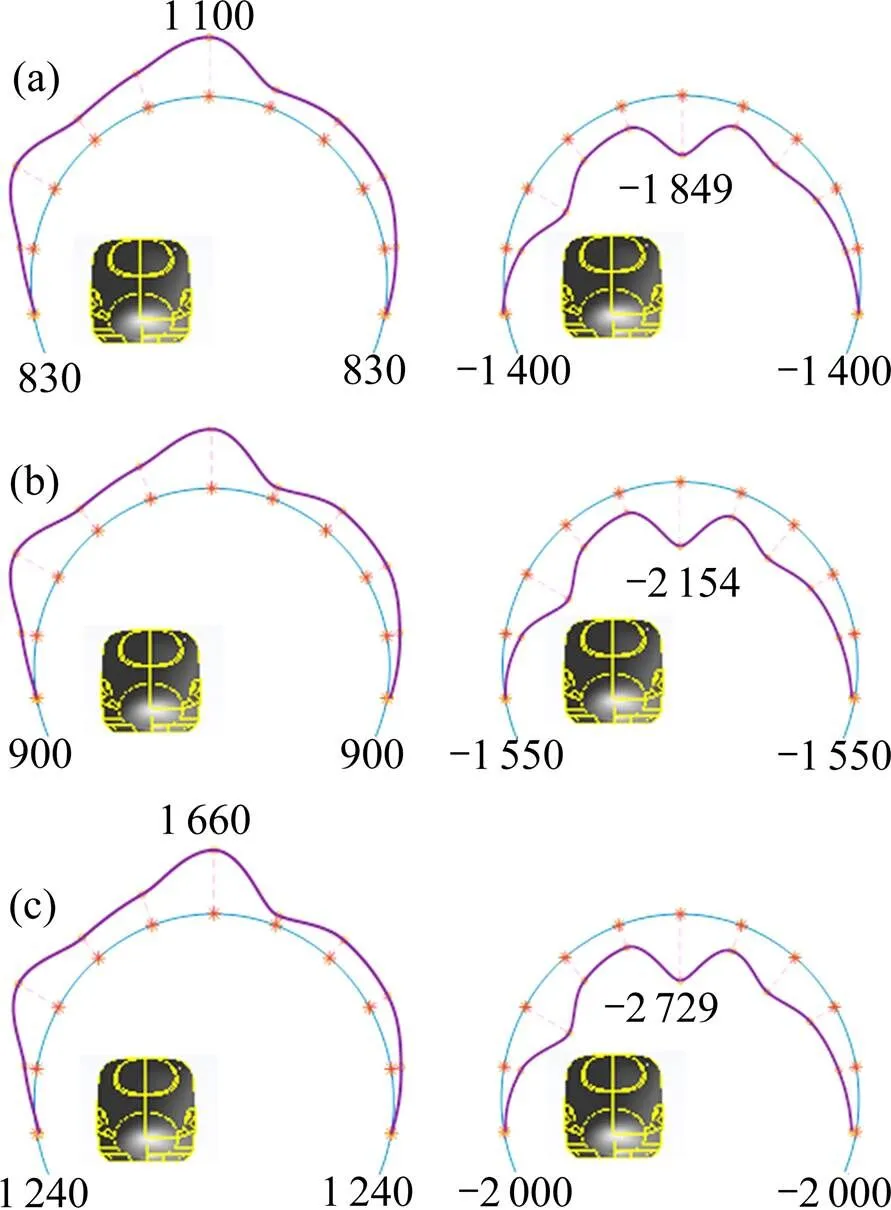
单位：Pa

3 结论

1) 列车通过全封闭声屏障时，由列车风导致的声屏障内部风压变化趋势与气压波的传播规律相吻合，可以很好地相互验证，证明了气压波传递的一维效应和该模拟的有效性。

2) 不同阻塞比下，同一位置不同测点的气动荷载波动规律基本一致，但对风压荷载极值影响显著，当阻塞比从9.6%分别增加到10.6%和11.8%时，声屏障最大压差幅值平均增加16.9%和48.3%，呈指数增长。

3) 各阻塞比下声屏障中间断面的极值风压荷载最大，为荷载控制截面，沿两端出入口方向极值风压逐渐减小；同截面声屏障上环向测点的风压变化趋势基本一致，但同一截面风压大小存在显著差异，最高达到45%。

[1] 辜小安, 李耀增, 刘兰华, 等. 我国高速铁路声屏障应用及效果[J]. 铁道运输与经济, 2012, 34(9): 54−58. GU Xiaoan, LI Yaozeng, LIU Lanhua, et al. Application and effect of high speed railway sound barrier in China[J]. Railway Transport and Economy, 2012, 34(9): 54−58.

[2] 周强. 高速铁路减载式声屏障隔声性能研究[D]. 成都:西南交通大学, 2015. ZHOU Qiang. Study on the sound insulation performance of high-speed track reducing load noise barriers[D]. Chengdu: Southwest Jiaotong University, 2015: 10−20.

[3] 李晏良, 李耀增, 辜小安, 等. 高速铁路声屏障结构气动力测试方法初探[J]. 铁道劳动安全卫生与环保, 2009, 36(1): 22−26. LI Yanliang, LI Yaozeng, GU Xiaoan, et al. Preliminary study on the test method of aerodynamic force for the noise barrier structure of high-speed railway[J]. Railway Occupational Safety Health & Environmental Protection, 2009, 36(1): 22−26.

[4] CHEN Xiaodong, LIU Tanghong, ZHOU Xisai, et al. Analysis of the aerodynamic effects of different nose lengths on two trains intersecting in a tunnel at 350 km/h[J]. Tunneling and Underground Space Technology, 2017, 66(1): 77−90.

[5] NIU J, ZHOU D, LIU F, et al. Effect of train length on fluctuating aerodynamic pressure wave in tunnels and method for determining the amplitude of pressure wave on trains[J]. Tunnelling and Underground Space Technology, 2018, 80(8): 277−289.

[6] ZHANG L, LIU H, Stoll N, et al. Influence of tunnel aerodynamic effects by slope of equal-transect ring oblique tunnel portal[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017(169): 106−116.

[7] 韩珈琪, 肖新标, 何宾, 等. 不同形式声屏障动态特性研究[J]. 机械工程学报, 2013, 49(10): 20−27. HAN Jiaqi, XIAO Xinbiao, HE Bin, et al. Study on dynamic characteristics of sound barriers[J]. Journal of Mechanical Engineering, 2013, 49(10): 20−27.

[8] 李志伟, 梁习锋, 张键. 横通道对缓解隧道瞬变压力的研究[J]. 铁道科学与工程学报, 2010, 7(4): 37−41. LI Zhiwei, LIANG Xifeng, ZHANG Jian. Study of alleviating transient pressure with cross passage in a tunnel[J]. Journal of Railway Science and Engineering, 2010, 7(4): 37−41.

[9] 王英学, 常乔磊, 任文强, 等. 间缝式开口隧道缓冲结构气动特性分析[J]. 铁道科学与工程学报, 2018, 15(1): 17−23. WANG Yingxue, CHANG Qiaolei, REN Wenqiang, et al. Seam opening tunnel buffer structure aerodynamic characteristic research[J]. Journal of Railway Science and Engineering, 2018, 15(1): 17−23.

[10] 骆建军, 吴尽, 陈鹏飞. 高速铁路并联隧道横通道对隧道内压力变化的影响[J]. 北京交通大学学报, 2015, 39(1): 8−13. LUO Jianjun, WU Jin, CHEN Pengfei. Pressure change from the cross aisle when the train passing through parallel tunnel of high-speed railway[J]. Journal of Beijing Jiaotong University, 2015, 39(1): 8−13.

[11] 马辉, 吴剑, 高明忠, 等. 基于气动效应的特长隧道断面优化探讨[J]. 隧道建设(中英文), 2019, 39(9): 1412− 1422. MA Hui, WU Jian, GAO Mingzhong, et al. Optimization of cross-section of extra-long tunnel based on aerodynamic effect[J]. Tunnel Construction, 2019, 39(9): 1412−1422.

[12] 吴剑, 万晓燕, 史宪明. 考虑车内瞬变压力指标的城际铁路隧道净空面积研究[J]. 科学技术与工程, 2015, 15(18): 104−110. WU Jian, WAN Xiaoyan, SHI Xianming. Study on intercity railway tunnel cross-section based on transient pressure inside train[J]. Science Technology and Engineering, 2015, 15(18): 104−110.

[13] YANG W, DENG E, LEI M, et al. Flow structure and aerodynamic behavior evolution during train entering tunnel with entrance in crosswind[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018(175): 229−243.

[14] LI X H, DENG J, CHEN D W, et al. Unsteady simulation for a high-speed train entering a tunnel[J]. Journal of Zhejiang University-SCIENCE A, 2011(12): 957−963

Numerical simulation of the influence of the section size of the fully-enclosed sound barrier on aerodynamic load

YANG Bin1, MA Xizhang2, GUO Kezhen3, HE Xuhui3, 4, JING Haiquan3, 4

(1. China Railway, Beijing 100844, China;2. Xiong’an High Speed Railway Co., Ltd., Baoding 011700, China;3. School of Civil Engineering, Central South University, Changsha 410075, China;4. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China)

In order to study the aerodynamic effect induced by the high speed train passing through the fully-enclosed sound barrier and to explore the influence of the cross-section area on aerodynamic load of the sound barrier, this paper simulates the process of a high-speed train passing through the full closed sound barrier with different clearance areas under the speed of 350 km/h using the computational fluid dynamics software FLUENT. The propagation law of pressure wave, the change law of aerodynamic load of sound barrier and the pressure distribution on typical measuring section were analyzed. The simulation results verify that the propagation law of the air pressure wave in the sound barrier is similar to that in tunnels. The variation curve of maximum value of the aerodynamic pressure of sound barrier changing with the section area is obtained. In addition,it is observed that the maximum value of the aerodynamic pressure has an inhomogeneous distribution in the same section. The research results provide the theoretical basis for the structural design of fully-enclosed sound barrier.

fully-enclosed sound barrier; 350 km/h high speed railway; section size; numerical simulation; aerodynamic load distribution

U491

A

1672 − 7029(2020)12 − 3013 − 08

10.19713/j.cnki.43−1423/u.T20200141

2020−02−24

国家重点研发计划项目(2017YFB1201204)；中国铁路总公司科研课题(P2018G004)；国家自然科学基金“杰青”资助项目(51925808)；国家自然科学基金资助项目(U1934209)；中南大学研究生科研创新项目(1053320182068)

敬海泉(1987−)，男，重庆人，副教授，博士，从事桥梁风致振动及其控制、斜拉索风雨振、尾流驰振机理及其控制措施研究；E−mail：hq.jing@csu.edu.cn

(编辑 涂鹏)