国际旅游列车开行方案优化研究

马振国，聂磊，张新，李翠萍

国际旅游列车开行方案优化研究

马振国1，聂磊1，张新2，李翠萍1

(1. 北京交通大学 交通运输学院，北京 100044；2. 中国铁道科学研究院集团有限公司 运输及经济研究所，北京 100081)

我国出境旅游需求不断增加，国际旅游市场巨大，既有国际旅客列车没有协同考虑运输组织与旅游方案，铁路国际旅游缺乏有市场竞争力的中高端产品。为拓展铁路国际旅游市场，亟需设计集运输组织优化与旅游效用提升于一体的国际旅游列车开行方案。通过重点研究线路节点备选集生成、运行线路与开行方案一体化设计优化、线路对比评价3个关键技术问题。首先通过优选指标体系和聚类分析筛选各国一级节点作为备选集；其次建立以旅游与运输效用最大化为目标的运行线路与开行方案一体化优化模型；最后案例分析中对同一线路开行方案进行对比，采用熵权TOPSIS模型对不同线路进行优度评价。本文为国际旅游列车开行方案优化提供了模型与方法，弥补了运输与旅游一体化研究的不足，研究结果可支撑国际铁路旅游市场的产品设计与开拓。

铁路运输；国际旅游列车；运行线路；开行方案；优化模型

当下出国旅游需求的增长促使国际旅客列车向运输与旅游综合体的方向发展。因此，研究建立一套结合运输和旅游的国际旅游列车开行方案设计方法，对于填补我国铁路在这方面的空白、服务国家“一带一路”战略具有重要的意义。国外旅游列车发展时间较早，如日本“七星”列车、俄罗斯“金鹰西伯利亚”快车、非洲之傲等，基本形成了一套集吃、住、行、游、娱等于一体的铁路客运产品，但这些列车也存在开行班次较少、时间不固定、时长较短(多为2～4 d)、价格昂贵等问题。本文的国际旅游列车是以中欧线路为背景，夜间行驶，白天到站游客下车游玩，提供吃、住、娱乐功能的兼顾开行径路、时间、停站方案等运输组织要素与旅游时间、内容等旅游要素的综合性列车，具有开行班次适中、时间固定、时长适度(多为8～15 d)等特点。鉴于此，本文需要研究的是国际列车开行方案(即旅游方案)设计优化问题。Moshe 等[1]认为旅游专列完成旅游点、景点、客运站形成“链条式”的运输服务。Jamie[2]详细论述了铁路政策和旅游交通的发展，并通过调研对游客的出行行为和偏好进行分析，探讨支线火车旅游的政策。이상재等[3]利用CVM法对铁路旅游线路进行盈利能力的评估，并量化了旅游列车乘客的满意度。熊伟丽[4]提炼出景点选择、创新、成本、老年游客等旅游专列产品的设计要点。刘昕宇[5]总结国外典型旅游列车产品在品牌、开行方案等方面的设计特点。针对旅客列车开行方案编制问题，Claessens等[6]建立了目标为开行费用最低的优化模型，并应用运筹学精确算法求解。YANG等[7]考虑铁路运营成本和乘客出行时空偏好，建立开行方案优化模型。唐洁等[8]构建高速铁路跨线列车开行方案优化模型，并从客流、区间能力等方面设计约束，利用遗传算法求解。龙品秀 等[9]以最大包络需求列车开行方案为备选列车集，建立不同需求日开行方案协同优化双层规划模型，利用遗传算法求解。针对旅游线路设计问题，LI 等[10]考虑时间、票价、游客偏好等约束，建立整数规划模型，求解成本最低旅行线路。伍雄斌等[11]通过定义旅游效用函数，建立旅游效用线路优化模型。综上所述，目前列车开行方案编制问题与旅游线路设计问题是独立研究的，实际运行线路与旅游线路一体化设计研究较少。本文针对这个问题，设计了线路节点备选集生成的流程，建立了运行线路与开行方案一体化设计优化模型，并进行案例求解，体现一体化优化的优势。

1 国际旅游列车运行线路与开行方案一体化优化问题描述

国际旅游列车运行线路的设计影响列车开行方案中的列车径路以及到发时刻的质量，列车开行径路选取影响旅游线路的成本及旅行时间。因此本文研究的主要问题是：给定起终点，在各国既有铁路线路的基础上，以旅游资源为导向，考虑旅客对列车到发时间、旅行时间、旅游成本等方面的的需求，寻找使得运输效用与旅游效用加权最大化的运行线路(即停站方案)。

1.1 线路方案的回程交通方式

由于国际旅游列车的去程旅游时间较长，考虑到游客有限的假期，旅客回程采用航空运输方式，这便涉及到回程机票票价问题，同时终点站也是游玩地之一，因此终点站的选择需综合返程票价与其他要素进行取舍。列车到达终点站后将在指定时间内在该节点等待客流集结，达到开行条件时，将沿原路返程。

1.2 节点备选集构建

本文中国际旅游列车的运行线路，同时也是旅游线路；构成运行线路的节点，同时也是旅游列车的停站。

运行线路节点(包括起终点)需要从节点备选集中选取。节点备选集的生成方法如下：

1) 选取中欧、中亚铁路通道沿线国家铁路网上的客运车站，构成各自国家的车站集合；2) 构建如图1所示节点优选指标体系(实线部分)，对每一个国家内部的客运车站进行指标计算，得出每个车站的选取数值；3) 依据选取数值，对每个国家所属车站进行聚类分析，进行级别划分；4) 选取一级节点作为每个国家的车站节点备选集；5) 在图1(实线部分)基础上，增加一个返程费用因素(虚线部分)，对各国备选集中拥有返回中国的国际机场的节点进行指标计算，筛选出各国最适合作为终点站的 节点。

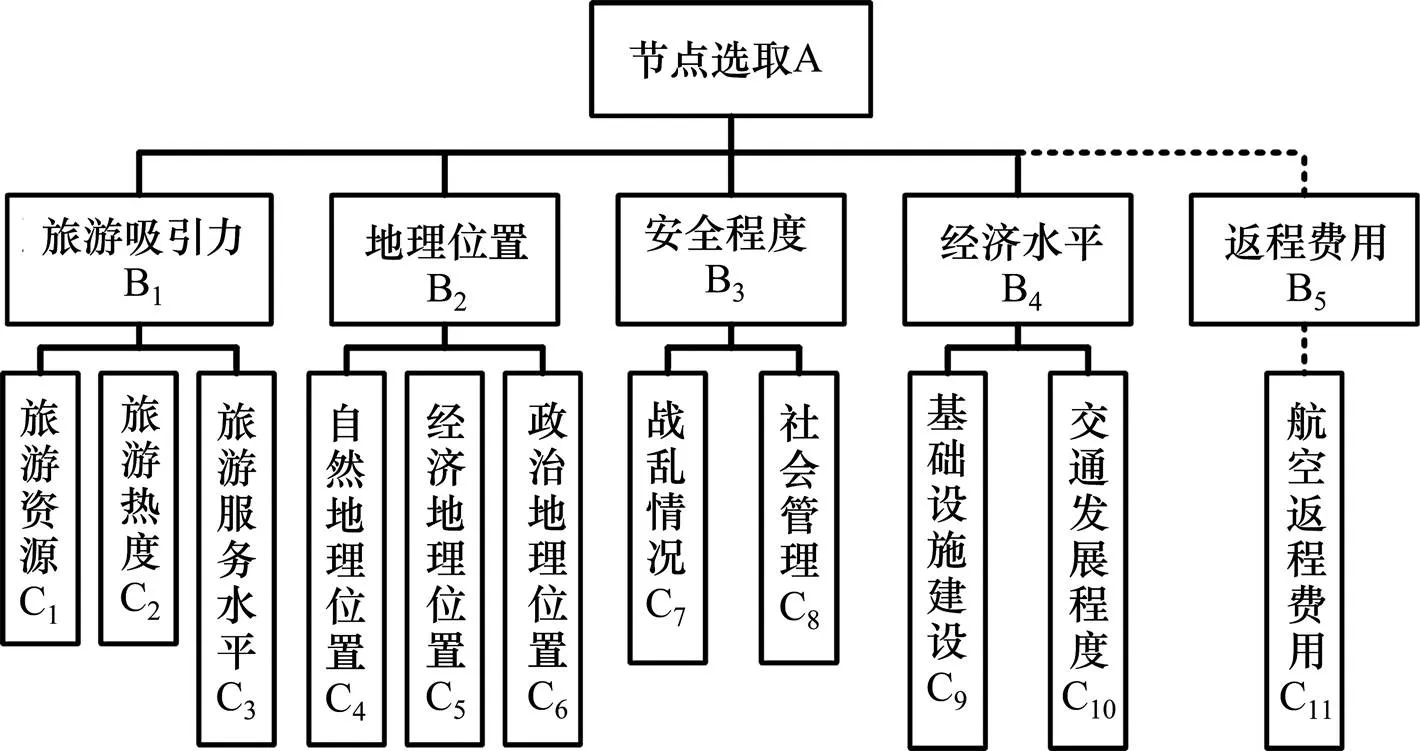
图1 节点优选指标体系

2 国际旅游列车运行线路与开行方案一体化设计优化模型

本章以旅游效用和运输效用最大化为目标，以时间、成本等为约束构建旅游列车运行线路与开行方案一体化优化模型。

2.1 模型假设

1) 各节点之间的铁路线路信息已知；

2) 各节点最佳旅游时间范围已知；

3) 列车旅速已知，取100 km/h；

4) 对各国线路能力影响不计；

5) 沿线各国车站有能力接发旅游列车；

6) 鉴于客流只在始发终到站，沿线无额外客流，因此不考虑客流量的影响。

2.2 模型参数及变量

2.2.1 参数

W(s)为运输效用，以到达时间和游客理想的到达时间区间相比较得出；

R为节点s的综合得分，表示节点旅游效用，是结合节点优选因素和问卷调查结果，从节点的核心竞争力、旅游影响度、游客偏好度、旅游主题特色、线路设施条件5个方面的综合得分，为保证与运输效用实现相同量纲，这里采用[0,1]之间的数进行标度，分度值为0.1；

为旅游与运输效用分权重之和；

t为列车从节点s到节点s的行驶时间，包含了列车起停车附加时分；

b为列车从城市节点s的出发时刻(包含日期)，统一转化为min；

e为列车到达城市节点s的时刻(包含日期)，统一转化为min；

T为在节点s期望游玩时间，由问卷调查获得，单位min，与R相关，综合得分大于0.8，游玩2 d，其余游玩1 d；

max为列车旅行全程时间上限，由问卷调查获得，取均值15 d；

t为节点s的换轨时间；

d为节点s到节点s的线路长度，单位km，线路长度取整数；

C为是否在节点s换轨，若列车在节点换轨，C=1，否则C=0；

为游客旅行全程所能接受的最大换轨次数，由问卷调查获得；

为缓冲时间的最大值，缓冲时间是指在每个城市避免行程安排过于紧密，提前确定的旅游时间可上浮的数值，这里取值720 min(12 h)；

1为游客理想的到达时间窗下限；

2为游客理想的到达时间窗上限；

为线路运行成本上界；

为停站数量；

1为旅游效用所占的权重；

2为运输效用所占的权重；

1为列车早于最佳到达区间到达产生的惩罚效用值；

2为列车晚于最佳到达区间到达产生的惩罚效用值；

1，2为列车出发时间下限和上限，与下一节点间距离有关；

2.2.2 变量

X为0-1变量，节点是否是节点的相邻的下一个节点，若是，则X=1，否则X=0；

2.3 目标函数

对于给定的线路主体方向上的各个国家城市节点备选集，每个节点包含综合得分R，游玩时间T，最佳到达时间区间[1,2]等属性。目标函数是要设计优化旅游与运输效用最大化的列车运行线路，构成线路的节点同时也是列车停站，因此停站方案也随之确定。目标函数由2部分组成：1) 起终点沿线所有停站综合得分的平均值，表示旅游效用； 2) 起终点沿线所有停站到达时间满意程度的平均值，表示运输效用。由于第1部分与第2部分重要程度不同，在进行列车开行方案优化时，需要对上述2部分赋予权重。

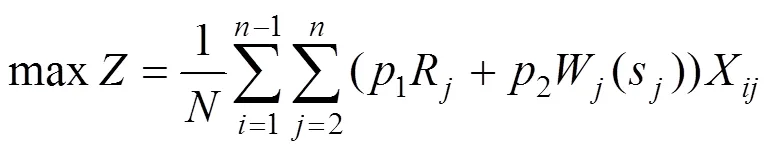
式中：W(s)的最大值为1，到达时间低于最佳区间下限时，每早到10 min效用值降低1；到达时间高于最佳区间上限时，每晚到10 min效用值降低2；到达时间位于最佳区间时，效用值为1。

2.4 模型约束

2.4.1 列车运行线路方向约束

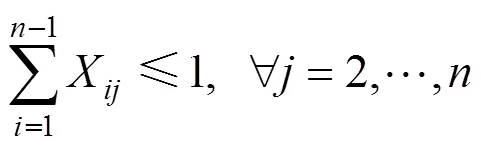
式(2)和式(3)保证了每个城市节点最多只能访问一次，且不能反向。

2.4.2 换轨次数约束

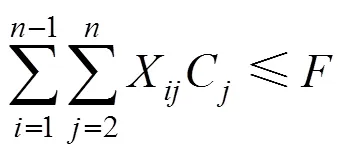
式(4)是对旅行全程游客所能接受的最大换轨次数约束。

2.4.3 相关时间约束

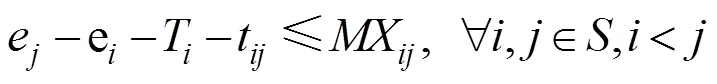
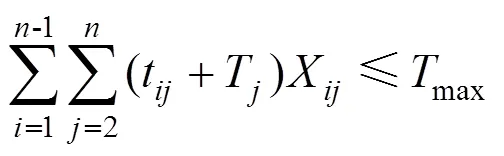
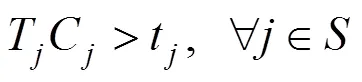
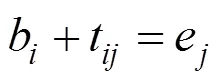
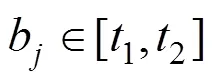
式(5)表示当X=1时，节点除了规定的游玩时间，还应具有因特殊情况需在节点增加的额外时间约束，保证时间的连通性；式(6)表示游客旅行全程所能接受的最大时间约束；式(7)为游客在有换轨需求的城市节点的游玩时间需要大于列车换轨时间约束；式(8)表示出发时间加上列车运行时间等于到达时间；式(9)表示开车时间范围(始发站不受约束)。

2.4.4 成本约束

式(10)表示列车运行的成本约束，考虑了线路等级、牵引方式、其他服务费用率等因素对成本的影响。

2.4.5 运输效用约束

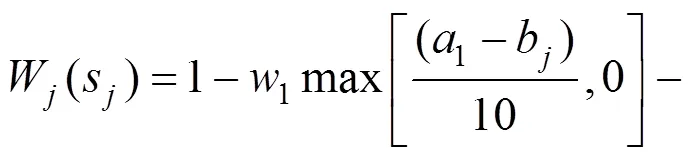
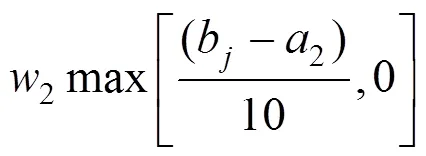
式(11)表示运输效用的计算约束，式中符号[]表示不超过的最大整数，max[,]表示不超过与之中的最大值的最大整数，W(s)大于等于0，利用式(11)求得值若为负数，默认值为0。

3 案例求解

3.1 参数获取及设置

为获取模型中关于游客旅游需求的参数值，设计《国际旅游列车调查问卷》。问卷包括4个部分：游客基本信息、旅游行为和消费特征、产品选择意愿、产品的需求，共计31个选项。问卷采取线上和线下发放形式，回收有效问卷2 105份。调查对象分布于不同年龄、职业、收入水平等，其中调查对象男性占51.3%，女性占48.7%，比例均衡，年龄以19～45岁的中青年为主，符合旅游市场特征。

问卷分析结果显示，旅客所能接受的最长旅游时间为15 d，平均每人每天花费上限1 000元。列车定员按200人计算，不妨设铁路最大成本占比5.5%。

虽然国际旅游列车为不占用白天旅游时间，一般以夕发朝至为主，但是中短距离不太合适，因此本文为列车出发时间范围制定了如下规则：d≥1 200，[1,2]=[20,21]；d∈[1 000,1 200]，[1,2]= [21,22]；d∈[500,1 000]，[1,2]=[22,23]；d∈[200,500]，[1,2]=[7,8]；d≤200，[1,2]=[8,9]余各参数具体取值如表1所示。

考虑列车国内始发，不再安排国内游玩，因此国内节点备选集只包含易于到达口岸站或本身是口岸站的城市。根据第1章中的节点备选集生成方法，生成以中欧、中亚、东欧为主，中东和中欧为辅的15个旅游国家的51个城市作为节点备选集，如表5所示，加粗部分为各国最适合作为终点站的节点。现指定线路起点为乌鲁木齐，终点为塔林。考虑到始发会经过换轨站，为方便旅客，指定列车始发时间为9:00。线路等级中，一类线路64元/列车公里，二类线路58元/列车公里，三类线路45元/列车公里；牵引方式中电力牵引50元/列车公里，内燃牵引60元/列车公里，其他服务费用率取值130元/列车公里。

表1 模型参数取值

3.2 运行线路与开行方案一体化设计优化结果及分析

本文所建模型通过Matlab求解。输出的运行线路(即停站方案)如图2所示，表2为优化后的列车开行方案及时刻表，表中(+1)表示停1 d，(+2)表示停2 d。该方案中共包含停站7个，运行区间8个，运行总里程6 941 km，深度游玩城市6个，旅游总时间14 d。

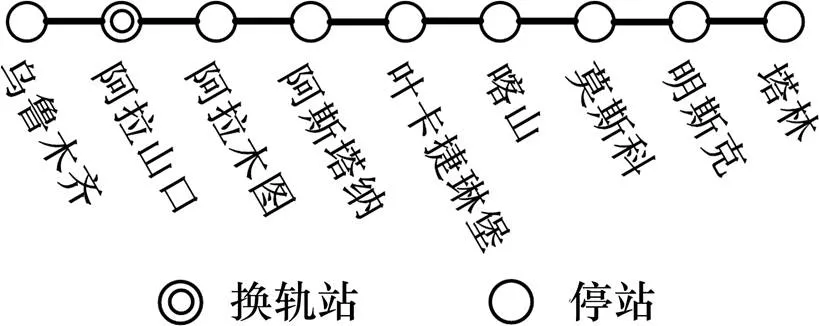
图2 最优运行线路(停站方案)

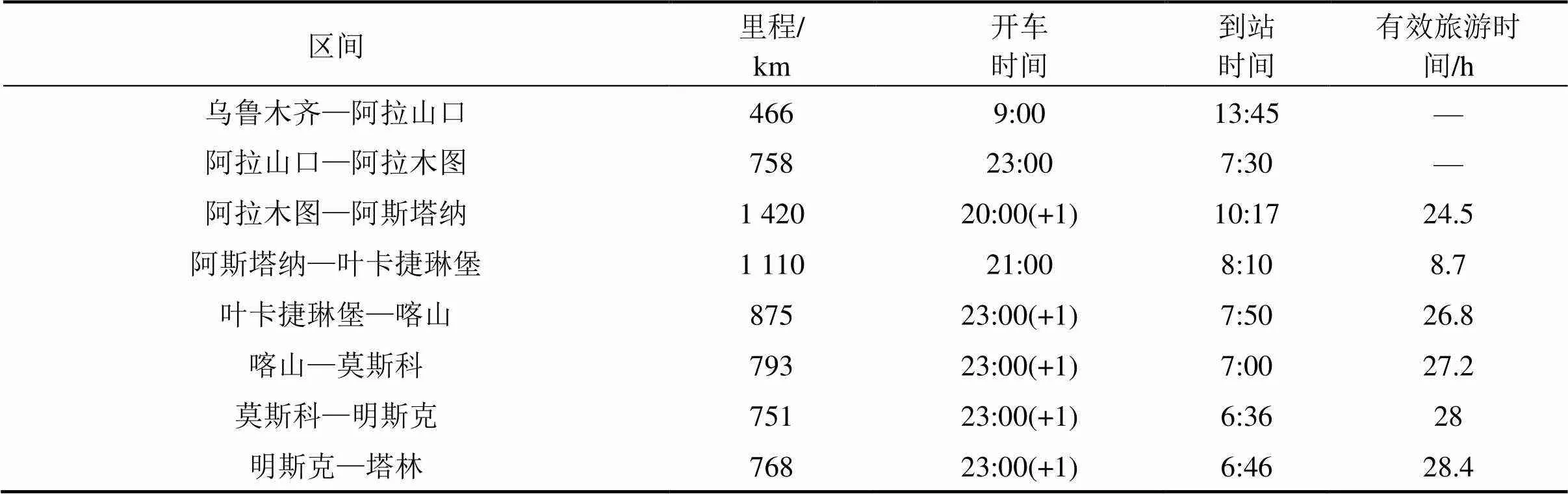
表2 优化后的列车开行方案

由于目前无此大范围的国际旅游列车，为体现一体化优化的效果，现在起终点不变的情况下，寻找另一条可行的运行线路，形成的开行方案(即优化前的开行方案)如表3所示。

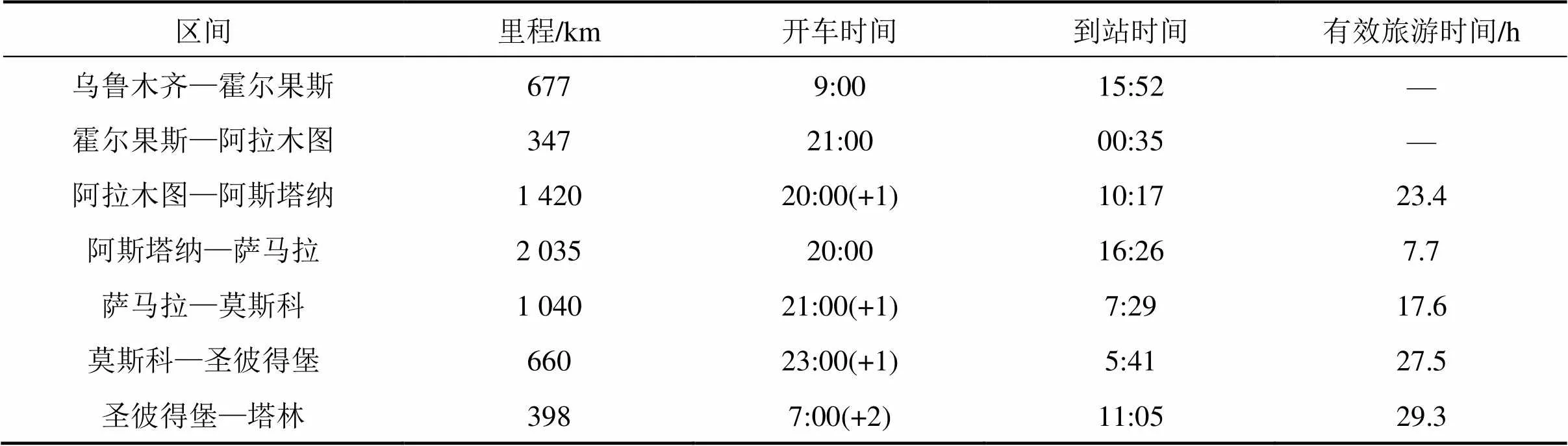
表3 优化前的列车开行方案

一体化优化后的列车开行方案与优化前开行方案的效果评价指标对比见表4。与优化前的开行方案相比，除去国内始发的2个非旅游节点，经计算，列车停站数增加1个，运行总里程增加5.53%，成本增加5.42%，旅游时间增加2 d。旅游效用值提高7.58%，运输效用值提高370.59%。在简单考虑1 d之中除去睡眠时间8 h，餐饮时间2 h后，平均每个城市有效旅游时间增加22.89%。

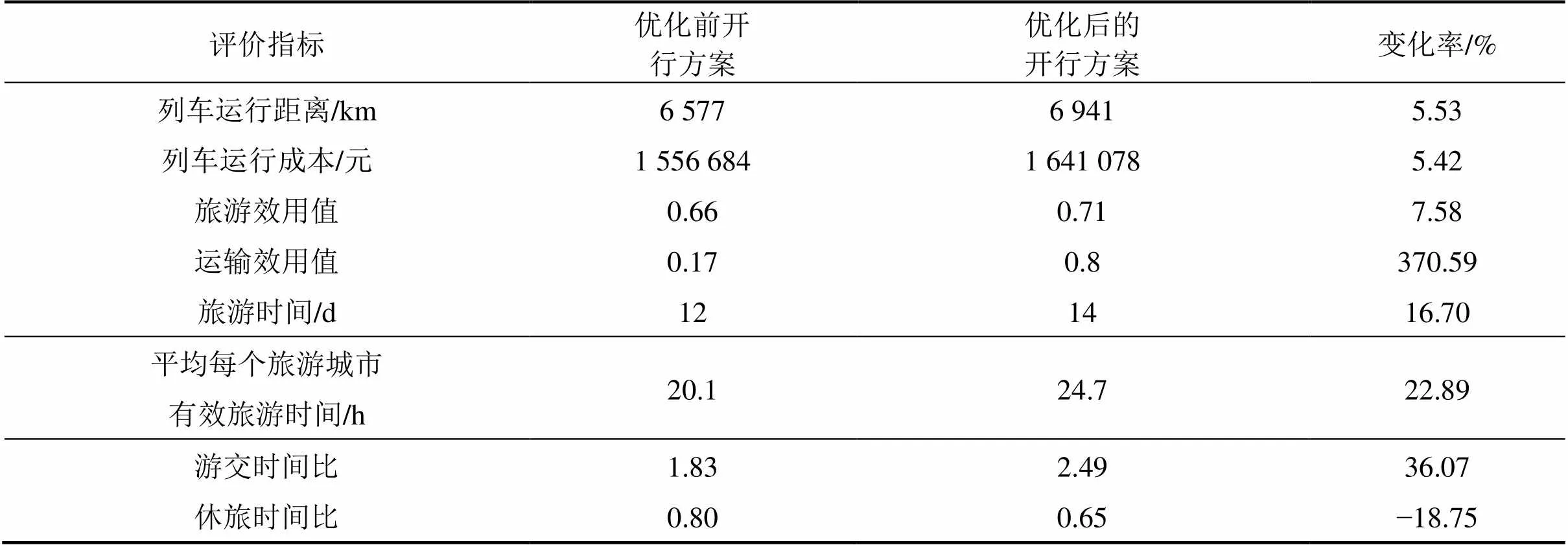
表4 列车开行方案效果指标对比

从旅游学角度，对比游交时间比(游玩时间与列车行驶时间的比)，优化后的开行方案提升了36.07%，减少了行车时间过长的情况，降低游客疲惫感；休旅时间比(夜间休息与白天游玩时间之比)方面，优化后的开行方案降低了18.75%，游客白天游玩时间变长，自主游玩时间相应增多。

综合来看，虽然优化后线路的成本提高，但优化后线路上减少了特色相近的节点，旅游效用值提升的同时，时刻表中到达时间点更为合理，满足游客需求的到达时间占比达到75%，运输效用值提升显著。优化结果一方面更加符合旅游列车夜间行车，白天到站游玩的原则，另一方面最大程度地满足了游客运输与旅游需求，减少了因运行时间过长导致到达时间点偏晚和运行时间过短导致到达时间偏早的情况，同时也说明了对于旅游列车来说最短路径或成本最低的路径并不一定是最优选择。

表5 国家及城市节点备选集

3.3 起终点不同线路之间的评价对比

现另指定集宁—鄂木斯克、乌鲁木齐—土库曼巴希、乌鲁木齐—索契等7个不同距离的OD对，在参数不变的情况下，利用一体化优化模型输出另外7条线路(线路8为上节优化的线路)。

为对比不同OD之间的线路，本文建立如图3所示的线路评价体系，基于熵权TOPSIS模型并利用模糊数学评价结果。详细步骤如下。

1) 构建加权评价矩阵：

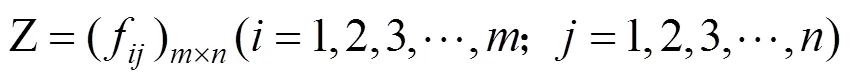
2) 确定评价指标的理想解：

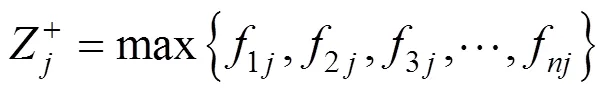
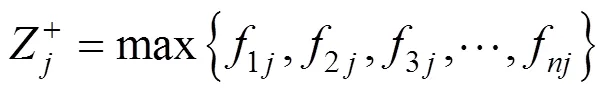
3) 计算各方案与正负理想解欧氏距离：

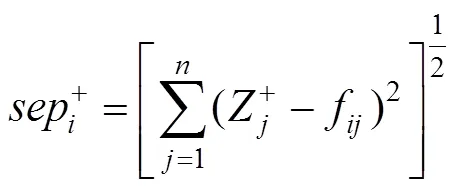
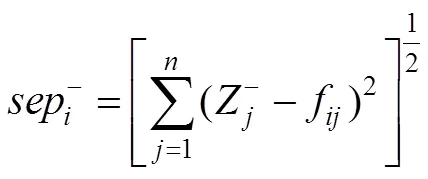
4) 计算方案与理想解的接近度指数C：

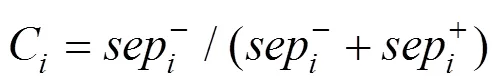
5) 模糊数学法评价结果的可靠性：

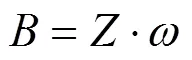
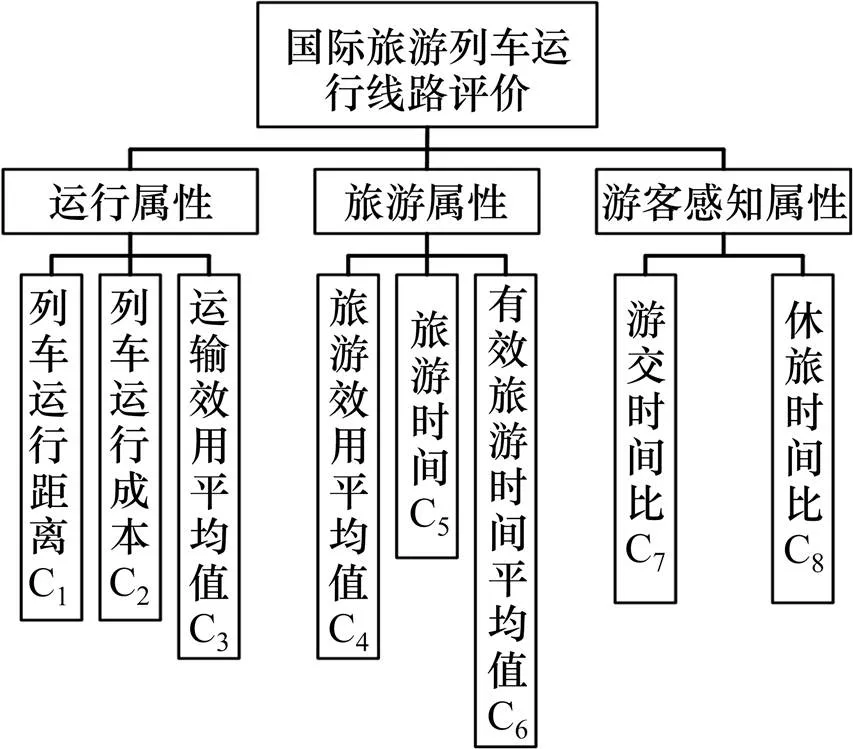
图3 国际旅游列车线路评价指标体系

根据式(12)～(18)计算出的评价结果如表6、表7所示。由表6可知，运行属性权重＞旅游属性权重＞游客感知属性权重。8个指标中，运输效用与旅游效用所占权重最大，侧面证明一体化优化模型中目标函数构建的合理性。

从表7来看，线路8指标优势明显，7，6和5指标相近，其次是线路1和4，最后是线路2和3。利用模糊数学法评价基于熵权法的结果可靠性高。铁路部门在实际规划运行线路时，应避免指标在0.1～0.2之间的线路，多规划指标在0.6以上的线路，同时着重提升运输效用。

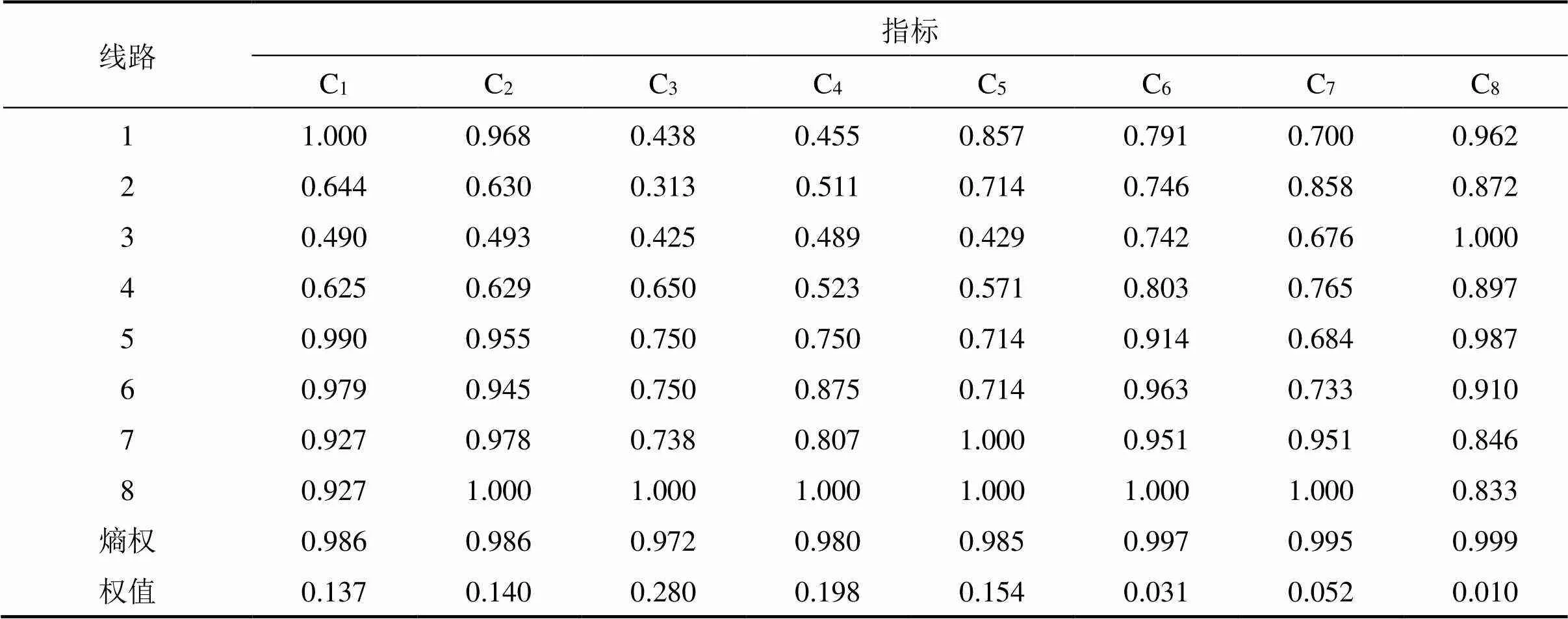
表6 评价指标标准化矩阵、熵值及权重

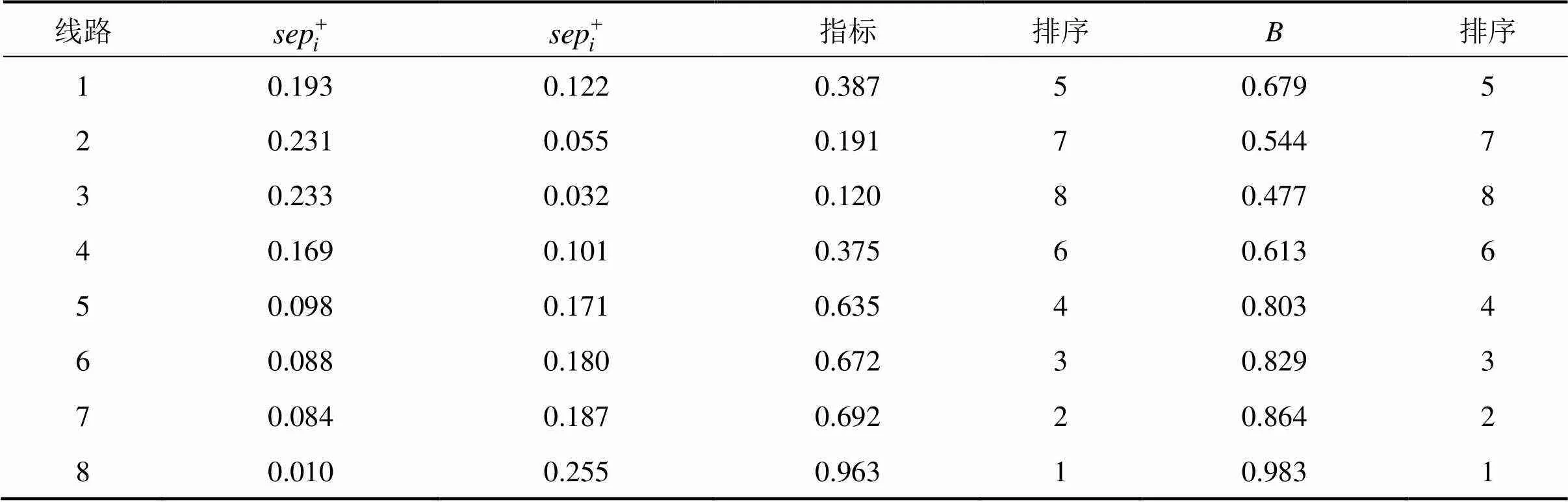
表7 国际旅游线路综合评价结果

4 结论

1) 针对国际旅游列车与普通列车在线路、节点方面的区别，设计了运行线路(旅游线路)节点(停站)备选集的生成方法。

2) 建立了运行线路与开行方案一体化设计优化模型，体现了节点选取影响列车径路和到发时刻质量，列车径路影响旅游线路成本与旅游时间，将旅游与运输效用最大化。

3) 优化后列车开行方案与非最优开行方案对比体现了一体化优化的优势，成本最小或路径最短并不一定是最佳选择，同时不同线路的评价对比体现了运输效用与旅游效用值是线路优劣的关键。本文研究为国际旅游列车运行线路及开行方案的制定优化提供了有益的参考，但文中某些参数的设置及获取方法仍有待深入研究。

[1] Moshe Givoni, Piet Rietveld. The access joumey to the railway station and its passengers’ satisfaction with rail travel[J]. Transport Policy, 2007(14): 357−365.

[2] Jamie Dallen. The challenges of diverse visitor perceptions: rail policy and sustainable transport at the resort destination[J]. Journal of Transport Geography, 2007, 15(2): 104−115.

[3] 이상재,김현구,안세영. Study to estimate the economic value of railway services using a contingent valuation method focusing on tourist train service in Korea[J]. Journal of the Korean society for railway, 2017, 20(1): 120−127.

[4] 熊伟丽. 铁路旅游专列产品的设计要点及市场展望[J].铁道经济研究, 2017(4): 37−39. XIONG Weili. The key factors and prospective of railway tourist train[J]. Railway Economics Research, 2017(4): 37−39.

[5] 刘昕宇. 国外典型旅游列车产品特点及对我国旅游列车发展的启示[J]. 铁道经济研究, 2019(1): 35−38. LIU Xinyu. Features of typical foreign tourist trains and the enlightenment to tourist train’s development in China[J]. Railway Economics Research, 2019(1): 35−38.

[6] Claessens M T, Van Dijk N M, Zwaneveld P J. Cost optimal allocation of rail passenger lines[J]. European J Oper Res, 1998, 110(3): 474−489.

[7] YANG Yuxiang, LI Jie, WEN Chao, et al. A bi-level passenger preference-oriented line planning model for high-speed railway operations[J]. Transportation Research Record, 2018, 2672(10): 224−235.

[8] 唐洁, 杨信丰, 申恒宇. 高速铁路跨线旅客列车开行方案优化研究[J]. 铁道科学与工程学报, 2019, 16(3): 596−604. TANG Jie, YANG Xinfeng, SHEN Hengyu. Optimization study on high-speed railway cross-line passenger train plan[J].Journal of Railway Science and Engineering, 2019, 16(3): 596−604.

[9] 龙品秀, 史峰, 胡心磊, 等. 不同需求日高铁列车开行方案协同优化方法[J]. 铁道科学与工程学报, 2019, 16(2): 310−318. LONG Pinxiu, SHI Feng, HU Xinlei, et al.The collaborative optimization of multi-day line plannings for high-speed railway[J]. Journal of Railway Science and Engineering, 2019, 16(2): 32019,

[10] LI Xiang, ZHOU Jiadong, ZHAO Xiande. Travel itinerary problem[J].Transportation Research Part B, 2016(91): 332−343.

[11] 伍雄斌, 关宏志, 韩艳. 多约束下基于游客体验的旅游路线优化模型[J]. 科学技术与工程, 2018, 18(13): 8−13.WU Xiongbin, GUAN Hongzhi, HAN Yan. Tour route optimization model based on tourist experience under multi-constraints[J]. Science Technology and Engineering, 2018, 18(13): 8−13.

Research on optimization of international tourist train operation plan

MA Zhenguo1, NIE Lei1, ZHANG Xin2, LI Cuiping1

(1. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China;2. Transportation and Economics Research Institute, China Academy of Railway Sciences Corporation Limited, Beijing 100081, China)

At present, the demand for outbound tourism in China is increasing, and the international tourism market is huge. The existing international passenger trains do not consider the transportation organization and tourism plan in a coordinated way, and the railway international tourism lacks semi-high-end products which is market competitive. In order to expand the railway international tourism market, it is urgent to design an international tourist train operation plan that integrates transportation organization optimization and tourism utility. This paper focused on three key technical issues: the generation of spare selection of nodes, the integration design optimization of running line and operation plan, and the comparative evaluation of lines. First, the first-level nodes of each country were selected as the backup set through the optimal index system and cluster analysis. Second, an integrated optimization model of operation line was established to maximize the utility of tourism and transportation. Finally, in the case study, the same line operation scheme was compared, and the entropy weight TOPSIS model was used to evaluate the goodness of different lines. This paper provides models and methods for the optimization of international tourist trains, which makes up for the lack of integrated transportation and tourism research. The research results can support the product design and development of the international railway tourism market.

railway transportation; international tourist train; running line; operation plan; optimization model

U293.32

A

1672 − 7029(2020)12 − 3208 − 08

10.19713/j.cnki.43−1423/u.T20200146

2020−02−25

国家重点研发计划资助项目(2016YFE0201700)

聂磊(1970−)，女，湖南长沙人，教授，博士，从事高速铁路运输组织研究；E−mail：lnie@bjtu.edu.cn

(编辑 蒋学东)