四旋翼无人机执行器可重构性量化评价方法研究

申富媛，李炜，*

（1.兰州理工大学 电气工程与信息工程学院，兰州730050；2.兰州理工大学 甘肃省工业过程先进控制重点实验室，兰州730050；3.兰州理工大学 电气与控制工程国家级实验教学示范中心，兰州730050）

近年来，在军用和民用领域有着大量应用的四旋翼无人机（quadrotors Unmanned Aerial Vehicle，quadrotor UAV）引起了学术界的广泛关注［1-2］。随着对系统安全性的要求越来越高，容错控制在各领域取得了大量可喜的研究成果［3-7］。Quadrotor UAV机体价格较便宜，但是随机携带的检测设备通常价格高昂，且无人机在执行任务时，尤其是航空、救援等领域，要求具有高可靠和安全性。一旦无人机的部件发生故障，不仅会使系统性能下降，还有可能带来不可预估的人员伤亡和经济损失［8］。1982年，美国航空航天局（NASA）提出了可重构性概念，描述了故障系统的自主恢复能力［9］。对于实际系统，并非任何故障都可以通过容错控制的方法得以补偿，如若故障后系统的可重构性已很低，还继续采用重构补偿的方式就可能错失最佳决策时间，引发灾难性事件的发生。因此，对于故障系统，若能够及时准确地对系统可重构性做出评价，不仅可降低重构失败和不可重构的概率，更重要的是能够提高系统安全性，避免故障下发生不可挽回的损失。

可重构性描述的是故障系统的自主恢复能力，可重构性评价则是利用理论判据和数学描述，判断系统重构能力的有无或大小。目前，对于系统可重构性评价的方法主要包括：基于系统固有特性的Gramian矩阵评价方法［10-12］、模态能控度评价方法［13］和状态范数能控度评价方法［14-15］。基于Gramian矩阵评价方法最关键的是Gramian矩阵计算。然而针对实际系统，其存在两方面的不足：①Gramian矩阵的计算要求建立系统精确的数学模型，实际系统不可避免地存在未建模动态和参数摄动；②Gramian矩阵是在系统投入运行之前离线计算，运行之后若系统发生故障，则此矩阵的计算会失去实际意义。基于模态能控度的评价方法通常假设系统特征根两两相异，对于实际系统而言，此假设条件并非均能满足，因此利用该方法进行可重构性评价存在很大的局限性。基于状态范数能控度的评价方法的本质是时间最优控制问题，但对于实际系统很难获得精确的恢复域。

上述研究成果主要还是针对线性系统。现实中，几乎所有的控制系统都或多或少的具有非线性特征。如前述的quadrotor UAV就具有高度非线性，而且具有强耦合、静不稳定等特性，常被建模为一种典型的非线性系统［16］。因此，以其为对象，开展非线性系统的可重构性评价具有重要的实际意义。尽管有学者采用循环小增益［17］、李导数［18］等方法进行了非线性系统可重构性研究，但这些方法都局限于某种特定的系统，通用性较差。

据统计［19］，50%以上的执行器和传感器故障是利用观测器生成的残差信号进行故障诊断与隔离，并进一步实现故障重构与容错控制，而容错的成败取决于冗余水平的高低，即系统的可重构性水平。但是，目前采用观测器估计状态进行可重构性评价的研究还少有。若以此为基础同时开展可重构性量化评价，无疑是极有意义的。而针对不同系统选择或设计满意的观测器，则是可重构性评价的关键条件。考虑到quadrotor UAV是一种典型的非线性强干扰系统，飞行过程中极易产生参数摄动或者引发执行器故障，本文为此设计了一种对于不确定性和故障兼具鲁棒性的双滑模面观测器。

相似性度量是对2个事物之间相近程度的一种综合评定。当2个事物越接近，它们的相似性度量也就越大，而2个事物越相异，相似性度量也就越小。系统亦是如此，正常运行时实际状态趋近于期望状态，故障时实际状态会偏离期望状态。显然，偏离程度越严重，系统自主恢复能力越弱甚至会瘫痪，因而，相似度的大小在一定程度上可以体现可重构的程度。对于相似性进行度量通常采用的方法就是计算样本距离，不同方法各有优劣。实际控制系统通常是多变量且不同量纲的，而马氏距离的优点是不受量纲影响，排除了变量之间相关性的影响。因此，本文将采用马氏距离对系统可重构性进行量化评价。

综上，针对具有执行器故障的quadrotor UAV，本文首先在建立系统模型的基础上，设计了一种双滑模面鲁棒观测器对受不确定性和故障影响的实际状态进行准确估计；其次综合考虑执行器饱和及状态误差指标约束，采用马氏距离对估计状态和期望状态进行基于相似性度量的可重构性量化评价；最后仿真验证了本文方法的有效性。

1 系统建模和描述

图1为quadrotor UAV结构，4个旋翼带动无人机工作，同一对称轴上的2个旋翼为一组。前后螺旋桨（T1，T2）按顺时针方向旋转，左右螺旋桨（T3，T4）按逆时针方向旋转。为了使quadrotor UAV沿着xe或ye方向移动，通常需要一个俯仰角θ或滚转角φ。然后，通过推力差产生的力矩直接稳定俯仰角和滚转角。

为了便于描述quadrotor UAV的运动状态，需先建立合理且科学的运动学模型，地面坐标系（oe，xe，ye，ze）和机体坐标系（ob，xb，yb，zb）。静态变换矩阵R定义为

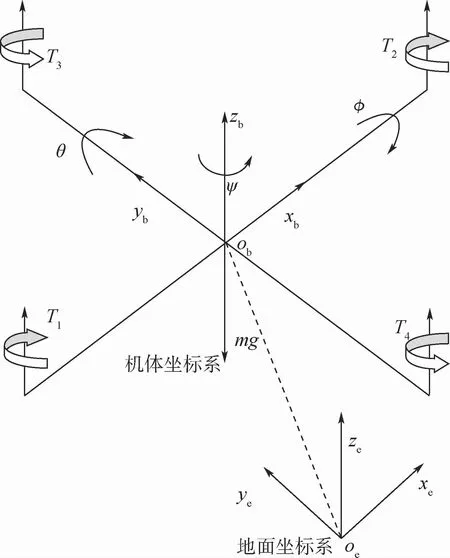
图1 quadrotor UAV结构Fig.1 Quadrotor UAV structure

2 双滑模面鲁棒观测器设计

基于观测器进行quadrotor UAV可重构性评价，其关键是要对系统的实际状态进行准确有效的估计。实际quadrotor UAV这一非线性系统在运行时不可避免地存在各种扰动和不确定性，若观测器不具备较强的鲁棒性，则估计的状态会受其影响，从而导致系统可重构性评价结果的不准确，最终影响重构或安全应急决策。因此，采用对扰动和不确定性具有鲁棒性的滑模观测器不失为一种好的选择。

若采用式（11）对quadrotor UAV进行状态估计，无故障时，较小不连续项v的引入即可对系统状态进行准确估计；一旦发生故障，由于鲁棒滑模观测器对故障具有灵敏性，则无法对故障quadrotor UAV的实际状态进行准确估计。若仍然按照上面的结果进行可重构性评价，评价结果会出现误报，失去指导意义。增大不连续项v的值，虽可以使得估计状态能够跟随实际状态，但是随着不连续项的增大，引入了抖动和高频干扰，进一步进行系统可重构性评价，致使评价出现偏差。

针对上述问题，本文将设计式（12）的基于2个不连续项的双滑模面鲁棒观测器，以期解决过分增大一个不连续项引起的抖动和高频干扰问题，使其同时对扰动和故障均具有鲁棒性。

注2 对于可建模为式（10），且满足条件1～条件5的任何系统，式（12）设计的双滑模面鲁棒观测器也适用。

3 可重构性量化评价

由于quadrotor UAV的实际状态（位置、姿态角及各自的变化率）不同量纲，最常使用的欧氏距离状态相似性度量方法不再适用，因此，本文采用基于马氏距离的相似性度量方法开展quadrotor UAV可重构性量化评价。

3.1 基于马氏距离的系统相似性度量

3.2 可重构性评价阈值选取

可重构性是指当系统发生故障后，系统的自主恢复能力，相似度的大小则反映了其可重构性

4 仿真验证

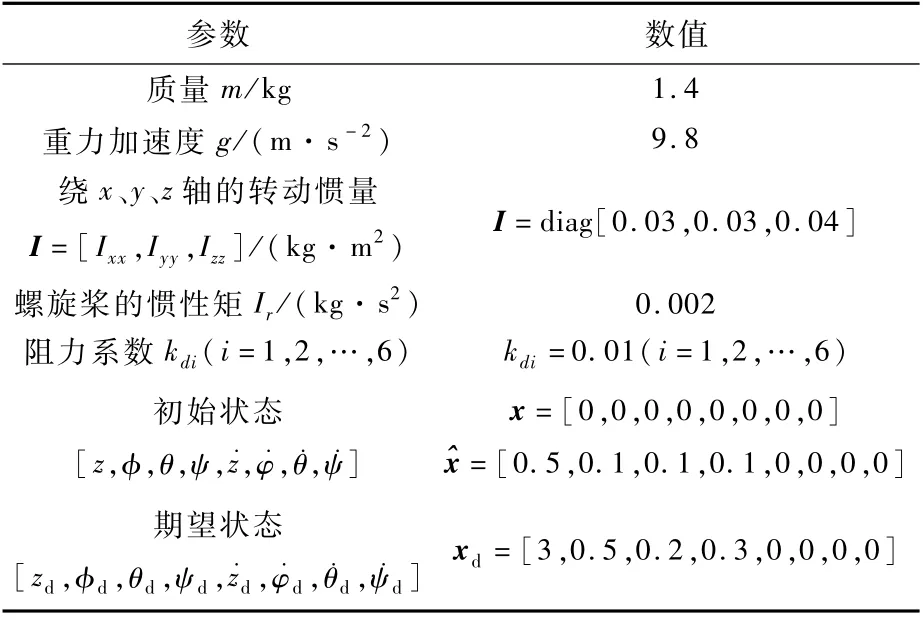
表1 quadrotor UAV物理参数Table 1 Physical parameters of quadrotor UAV

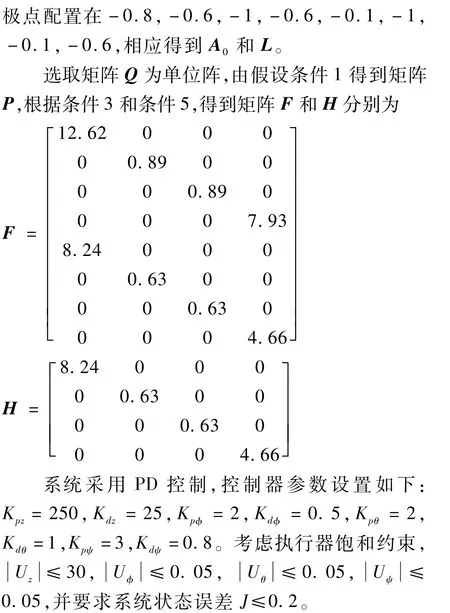
4.1 采用式（11）鲁棒观测器

图2 执行器无故障Fig.2 Failure-free actuator

假设t≥5 s时发生执行器故障，取κ=10，fa（x，u，t）=［15，0，0，0］。从图3可以看出，滑模观测器观测值发散，相应的残差信号也发散，若用此结果进行可重构性量化评价则会导致误报。

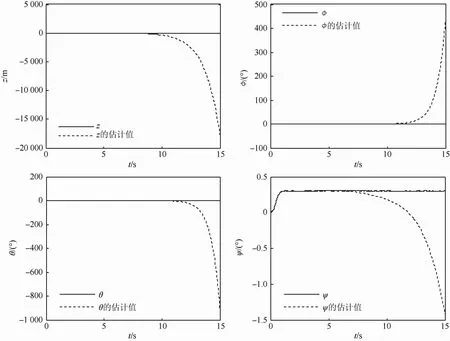
图3 执行器发生故障Fig.3 Actuator with failure

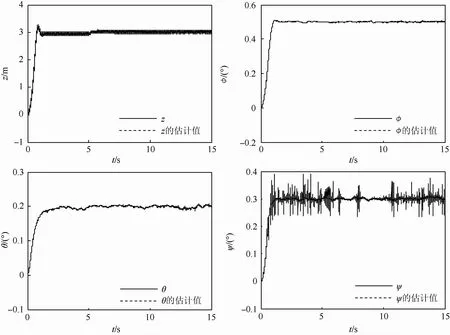
图4 调整不连续项Fig.4 Discontinuous term adjustment

4.2 采用双滑模面观测器

上述仿真结果是针对fa（x，u，t）=［15，0，0，0］故障情形，为了能够更好地验证本文方法的有效性，针对执行器单一和多故障情形，分别给出了可重构性评价结果，具体如表2所示。

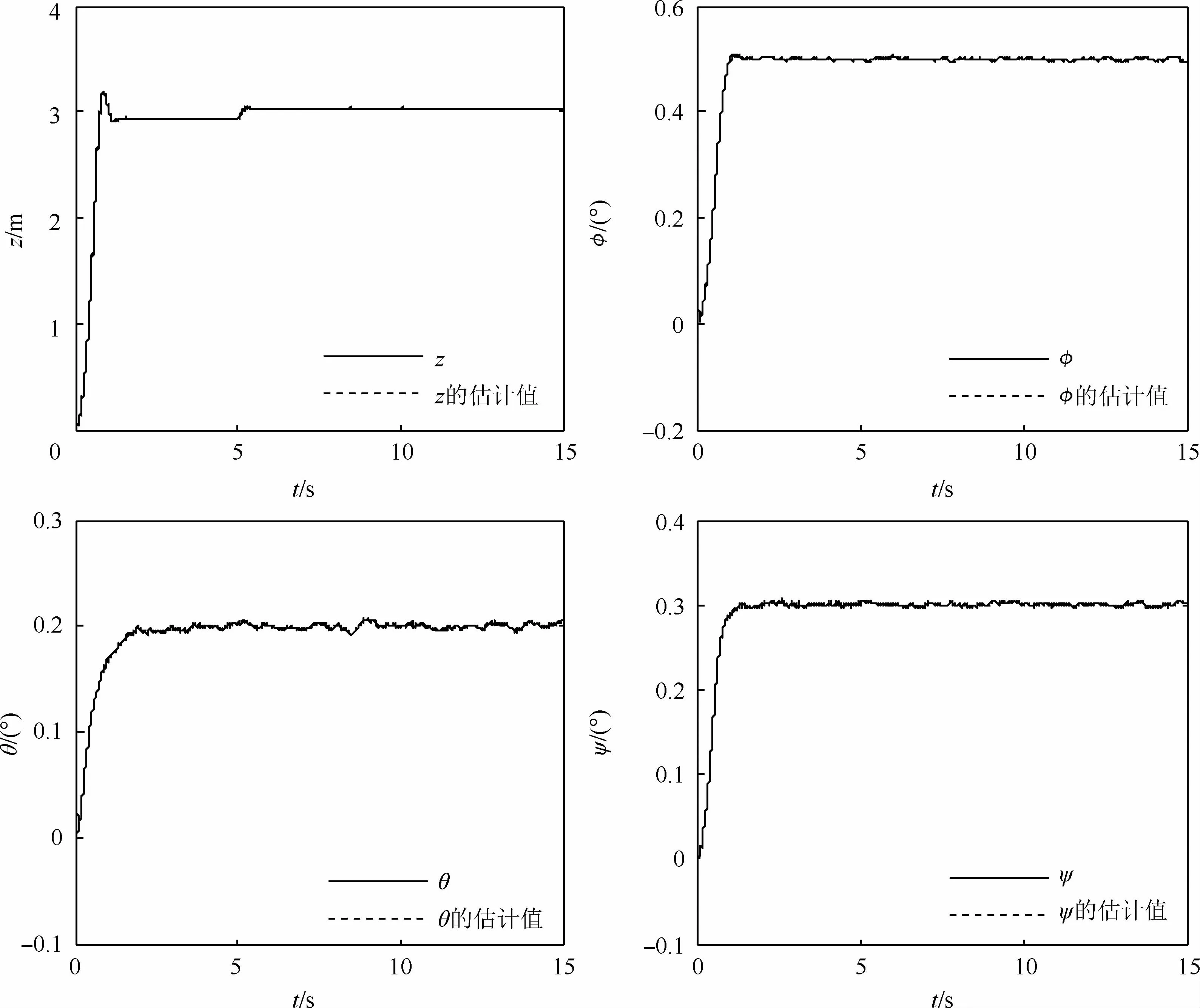
图5 双滑模面观测器Fig.5 Double sliding surface observer

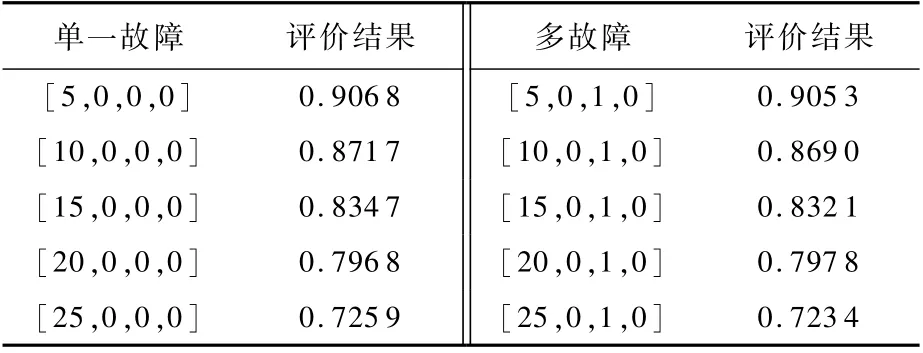
表2 执行器故障可重构性量化评价Table 2 Quantitative reconfigurability evaluation of actuator fault

由表2可知，从纵向来看，随着故障从小到大演变，可重构性评价结果亦逐渐变小；从横向来看，多故障情况下的可重构性较单一故障要小，结果符合一般的客观规律。

5 结束语

本文针对quadrotor UAV非线性系统设计了对故障和扰动均具有较强跟踪能力的双滑模面鲁棒观测器，在考虑执行器饱和及状态误差指标约束条件下，采用马氏距离相似度的方法对系统可重构性进行量化评价，并能自适应调整评价阈值，及时准确地对故障系统的可重构程度做出评估，确保系统的安全性。通过仿真验证了文中所述方法的正确性和有效性。由于建立的quadrotor UAV模型与一般的非线性系统描述一致，因此，该方法也适用于满足条件1～条件5的其他非线性对象。