无人机组合导航直接法与间接法滤波方式比较

王均晖，孙蕊，2，*，程琦，张文宇

（1.南京航空航天大学 民航学院，南京211106； 2.西安测绘研究所 地理信息工程国家重点实验室，西安710054）

精确的导航定位信息是实现无人机安全飞行的关键。惯性导航系统（INS）和全球导航卫星系统（GNSS）作为2种常用的导航系统，可以有效获取无人机实时导航定位信息，目前已经在无人机导航中被广泛应用。GNSS以全球定位系统（GPS）为代表，能够得到高精度的三维位置、速度；INS由计算机和惯性测量单元（IMU）组成，利用IMU提供的量测信息可以实现自主的导航解算。GPS/IMU通过滤波算法进行组合，算法通过对GPS和IMU数据进行估计、修正、融合，可以有效实现2个系统的互补更新，来解决GPS信号失锁引起的无法定位问题和IMU长时间积累误差引起的漂移问题，因此在无人机组合导航中具有非常重要的作用。

GPS/IMU组合导航根据滤波器的种类、输入传感器之间的耦合程度、滤波器的观测输入量的类型特征等因素可以进行多种分类。例如，以基于不同滤波器类别的组合导航方式可以分为：基于卡尔曼滤波系列的GPS/IMU组合导航［1-3］；基于粒子滤波的GPS/IMU组合导航［4-5］；以及基于多模态多联邦卡尔曼滤波的GPS/IMU组合导航等［6-8］。目前，已经有许多文献对基于不同类型滤波的组合导航进行了详细的对比分析研究。Georgy等分别利用卡尔曼滤波和粒子滤波将低成本INS与GPS进行组合，并在道路环境下测试这2种组合导航系统的性能［9］；陈坡等在仿真的飞机运动状态下，比较了自适应卡尔曼滤波和H∞滤波应用于GPS/IMU组合导航系统的可行性和有效性［10］；聂琦和高晓颖通过数值仿真，比较了使用不同等级的惯性传感器与GPS组合时sigma点卡尔曼滤波和扩展卡尔曼滤波（EKF）的优劣［11］。众多研究表明，滤波类型的不同对GPS/IMU组合导航的精度以及鲁棒性等方面有着重要的影响，在无人机高动态以及复杂环境的飞行情况下尤为显著。

基于GPS和IMU之间耦合程度不同可以分为松组合（位置、速度、姿态信息层面）、紧组合（观测量层面）和深组合（信号层面）。针对不同层面组合导航的比较分析较为成熟，仇立成等利用车载GPS/IMU组合导航的实测数据进行分析，发现紧组合较之松组合能获得更高的定位精度［12］；李妍妍比较分析了松、紧、深3种组合结构下的捕获跟踪和信息融合技术并进行了实例验证，从而更好地搭建组合导航数据处理平台［13］。其中，松组合具有结构简单、易于实现的优点；紧组合抗干扰能力强，可使系统快速收敛，从而达到较高导航精度，但结构相对复杂；深组合具有高精度、强抗干扰性，但系统复杂，实现难度大。

基于滤波器观测量特征不同的组合导航方式可以分为：基于直接法的组合导航方式和基于间接法的组合导航方式。其中，间接法以各导航子系统的误差量，也就是GPS和IMU输出的导航参数的误差作为滤波器的状态量从而进行滤波计算；直接法以各导航子系统的输出参数，即GPS和IMU输出的导航参数作为状态量来进行滤波估计。目前以直接法为组合导航方式的研究主要包括：李荣冰等设计了基于微型飞行器的GPS/IMU组合导航系统来验证sigma点直接式滤波方法的有效性和可靠性，仿真结果达到了5 m的定位精度［14］；逯峤等利用基于平方根中心差分卡尔曼滤波（SR-CDKF），解决了直接法滤波估计中姿态、速度和位置等导航参数的非线性问题，达到了分米级的定位精度［15］。文献［14-15］表明直接法建模的方式具有简单、直接的优点，并且在静态桥梁形变数据平滑、车辆运动估计等领域进行了有效的应用。同样，间接法也是一种常用的组合导航模式。徐田来等通过输入位置误差、速度误差以及姿态误差量，构建一种基于模糊自适应卡尔曼滤波的车载GPS/IMU组合导航系统，在仿真情况下将经纬度的误差控制在1″内［16］；吴富梅和杨元喜利用小波阈值消噪的自适应滤波削弱IMU误差的影响，有效地分离有用信号和噪声信号，提高了GPS/IMU组合导航系统的精度和可靠性，达到了0.6 m均方根误差（Root Mean Squared Error，RMSE）的定位精度［17］。

虽然间接法和直接法都在组合导航的工程实践中被广泛应用，针对这两者在不同场景条件下的比较分析却少有研究。李开龙等从系统模型、滤波算法以及应用等方面对组合导航的直接法和间接法进行了分析，通过车载实验，针对不同路况的数据评估各自导航性能，结果表明，高机动条件下可选择直接法，而静态和低速运动时应选择间接法，但是该结论并不适用于三维空间内无人机的飞行［18］。因此，为了进一步分析不同种建模方式，探索给定应用场景下2种建模方式的组合导航的性能差异，对算法的适用性有进一步的了解从而更好地服务于工程应用。本文在直接法和间接法的组合模式下，分别设计了基于EKF的GPS/IMU组合导航系统的算法，并基于仿真数据和实际数据对2种组合模式的算法精度进行详细地比较分析，为无人机在不同场景下的安全飞行提供有效的技术支撑。相对于载波相位的整周模糊度的难点，伪距法定位具有速度快、无多值性问题的优点，故本文利用伪距法对GPS进行定位解算。

1 基于EKF的组合导航模型构建

本节内容主要针对直接法和间接法组合模式，设计了基于EKF的GPS/IMU组合导航系统的算法。由于松组合结构简单、计算量相对较小，适用于对实时性要求较高的系统，因此将用松组合来比较分析无人机的组合导航系统在2种组合模式下的算法精度。

1.1 松组合直接法

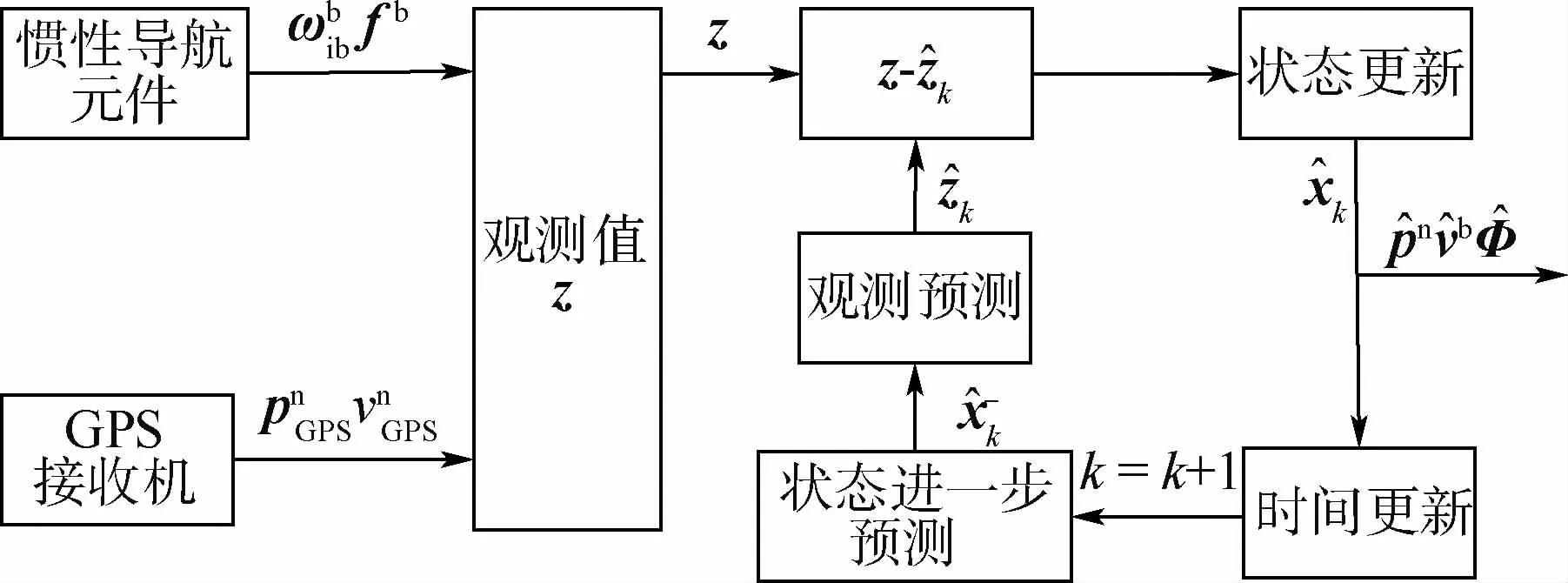
图1 直接法滤波Fig.1 Direct mode of filtering

1.2 松组合间接法

图2 间接法滤波Fig.2 Indirect mode of filtering

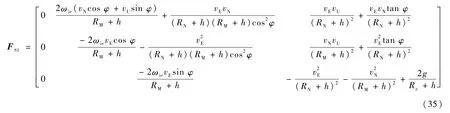
式中：ωie为地球自转角速度；h为大地高；f为加速度计输出的比力值；g为重力加速度；RM、RN和Re分别为地球的子午圈曲率半径、卯酉圈曲率半径和平均半径。

1.2.2 量测方程的建立

设vn=［vE，vN，vU］T为三维速度信息，下标E、N和U分别表示东向、北向和天向，上标I和G分别为该信息由INS和GPS输出，设λ，L和h分别为经度、纬度和高度，下标I和G分别为该信息由INS和GPS输出。间接法里所采用的量测方程将INS与GPS接收机给出的位置、速度信息的差值作为量测量。量测值为

2 实验仿真

本实验利用MATLAB构建仿真环境，生成无人机运动状态、GPS接收机输出以及惯性元件的测量值。无人机轨迹包含了上升、平飞、下降等多个航段，有利于本文全面地对直接法和间接法组合导航的定位精度进行评估。针对组合导航直接法和间接法的情形，分别利用EKF进行了仿真实验。其中，GPS的采样频率选取10 Hz，接收机误差包括热噪声、多路径以及电离层误差等，表1为INS的相关参数设置，频率选取100 Hz。

仿真实验中，导航信息的初始误差为：水平姿态误差20′，方位误差20′，位置误差1.5 m，速度误差2 m/s。初始航向角为90°，初始位置为北纬39°西经81°，海拔高度0 m。此外，为更好地评价组合导航系统的性能，本文设置无人机飞行过程中的丢星场景如表2、表3所示。图3为仿真无人机的三维飞行轨迹图，图4为仿真飞行轨迹的速度。

图5为丢星场景1下无人机的仿真飞行轨迹，包括参考轨迹、GPS接收机基于伪距解算得到的位置以及直接法和间接法滤波得到的轨迹。图6为组合导航系统在场景1下的位置误差。表4为场景1最大位置误差。结合图表可以看出，场景1下，直接法的位置误差可达上百米，尤其是转弯部分丢星的15 s，东向位置误差达到100 m，北向位置误差达80 m，天向位置误差达200 m；而间接法的位置误差，即使在丢星段，三维位置误差均控制在10 m内。

表1 惯性导航系统参数设置Table 1 Parameter setting of INS

表2 仿真环境下丢星场景1设置Table 2 Setting of lost star in Scenario 1 under simulation environment

表3 仿真环境下丢星场景2设置Table 3 Setting of lost star in Scenario 2 under simulation environment

场景1下，受丢星15 s影响，直接法和间接法位置误差的差距达到2个数量级，同时，第3节的真实数据验证部分，丢星均不超过5 s。因此，以下重点对场景2展开具体分析。

图7和图8分别为场景2下无人机的仿真飞行轨迹的平面图和高程图，包括参考轨迹、GPS接收机基于伪距解算得到的位置以及直接法和间接法滤波得到的轨迹。

图3 无人机的三维飞行轨迹Fig.3 3D flight trajectory of UAV

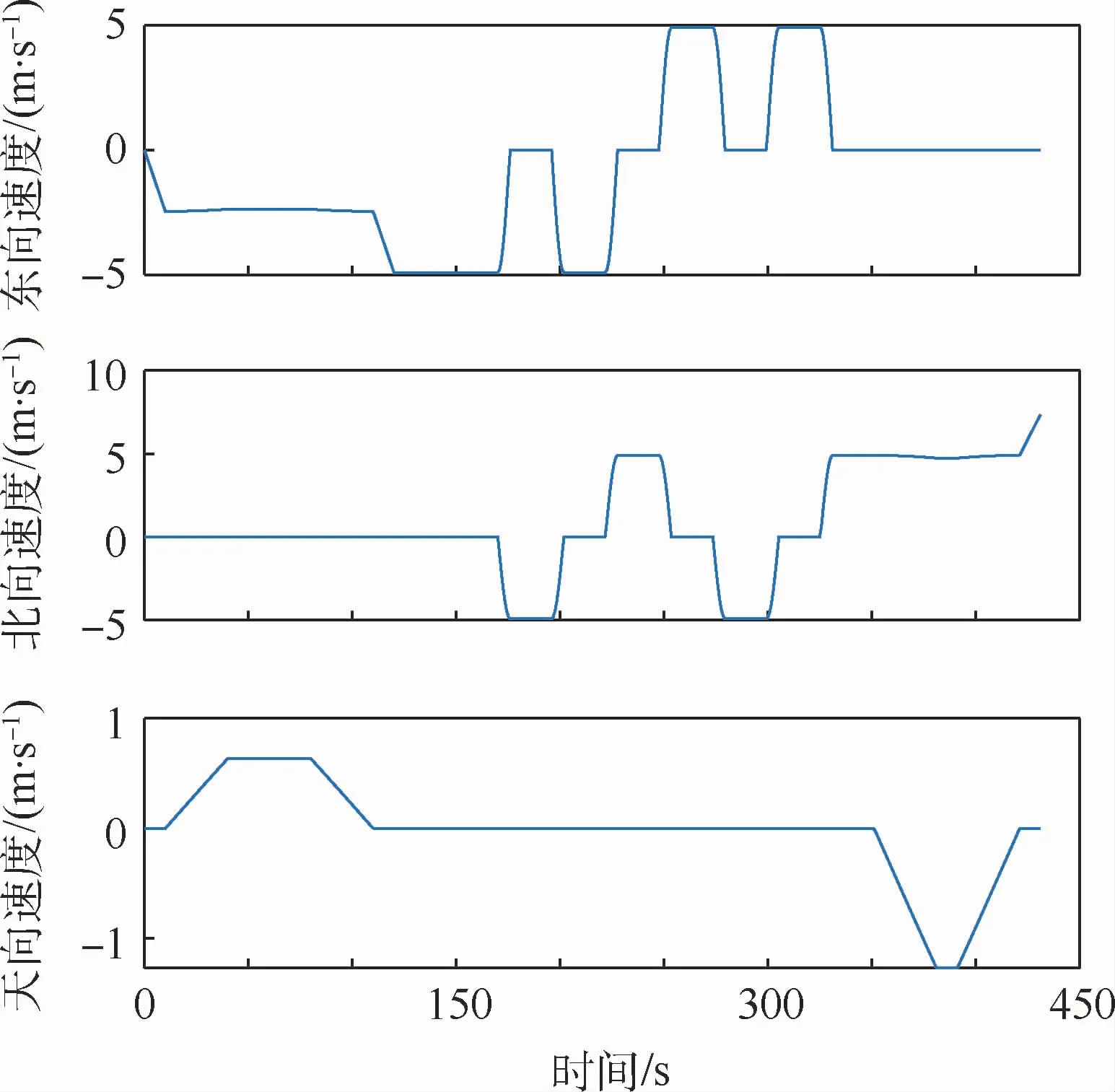
图4 仿真飞行轨迹的速度Fig.4 Velocity of simulated flight trajectory

图9为场景2下组合导航系统状态运动的位置误差，包括GPS位置相对于参考轨迹的差值、直接法和间接法滤波后各自的位置误差。图10和图11分别为组合导航系统在2种不同组合模式下的速度误差和姿态误差。

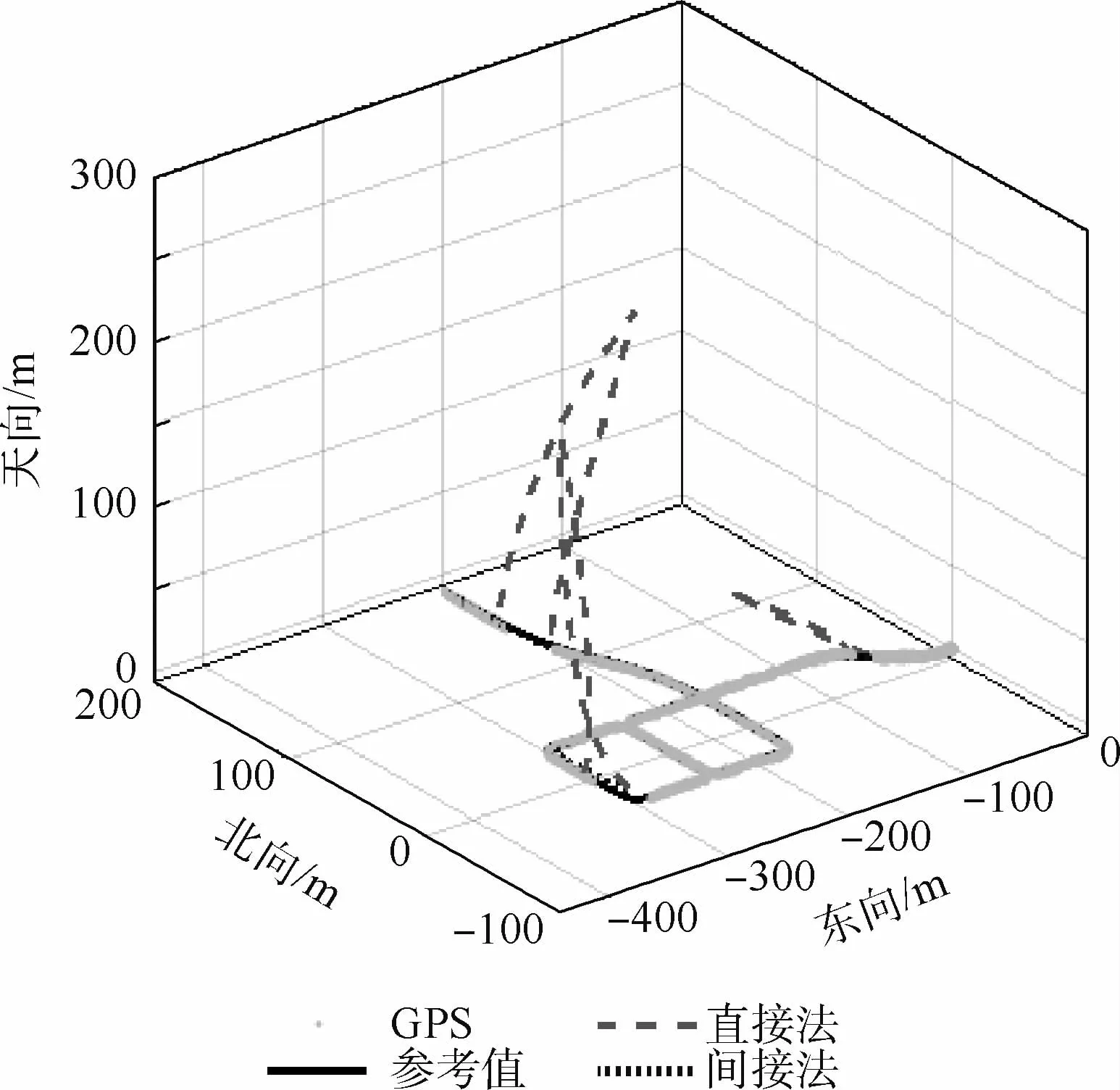
图5 场景1仿真飞行轨迹Fig.5 Simulated flight trajectory in Scenario 1

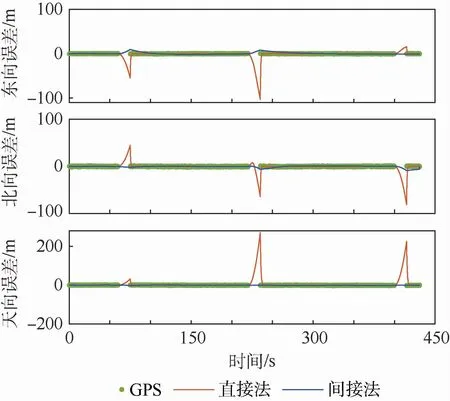
图6 场景1位置误差Fig.6 Position errors in Scenario 1

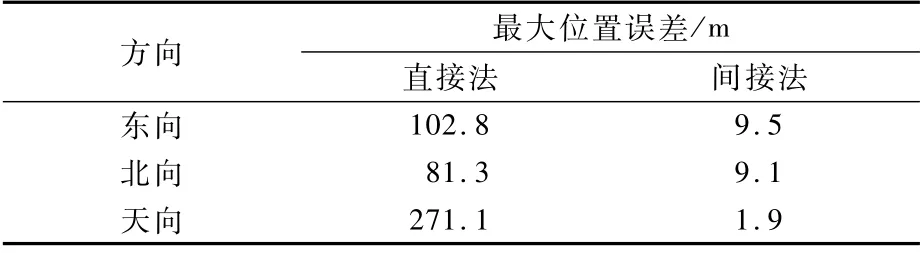
表4 场景1最大位置误差Table 4 Maximum position error in Scenario 1

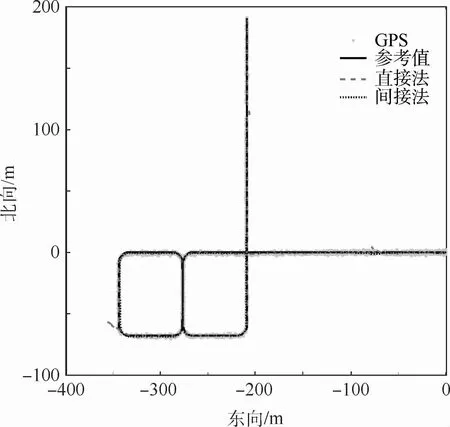
图7 场景2仿真飞行轨迹（水平维度）Fig.7 Simulated flight trajectory in Scenario 2（horizontal dimension）

图8 场景2仿真飞行轨迹（竖直维度）Fig.8 Simulated flight trajectory in Scenario 2（vertical dimension）

图9 场景2位置误差Fig.9 Position errors in Scenario 2

图10 场景2速度误差Fig.10 Velocity errors in Scenario 2

计算场景2下直接法、间接法和GPS的位置RMSE见表5。计算直接法和间接法的速度RMSE、姿态RMSE分别见表6、表7。仿真环境下直接法和间接法运行时间见表8。

图11 场景2姿态误差Fig.11 Attitude errors in Scenario 2

表5 场景2下直接法、间接法和GPS的位置RMSETable 5 Position RMSE of direct mode，indirect mode and GPS in Scenar io 2

表6 场景2下直接法和间接法的速度RMSETable 6 Velocity RMSE of direct mode and indirect mode in Scenario 2

表7 场景2下直接法和间接法的姿态RMSETable 7 Attitude RMSE of dir ect mode and indirect mode in Scenario 2

表8 场景2下直接法和间接法运行时间Table 8 Runtime of direct mode and indirect mode in Scenar io 2

总体来说，松组合直接法和间接法滤波分别达到了2.42 m和1.12 m的定位精度，速度误差分别为0.78 m/s和0.06 m/s，实验运行所需时间分别为10.38 s和24.30 s。若不考虑丢星部分，直接法的水平位置和垂直位置均方根误差值分别控制在0.55 m和0.85 m以内，间接法则控制在0.51 m和0.89 m。显然，在GPS不丢星的情况下，直接法和间接法对于定位精度的提高不分伯仲，这也验证了从本质上来说直接法和间接法同根同源，都是INS力学编排和卡尔曼滤波相结合的结果。然而，间接法在正式滤波之前需要进行惯导解算，直接法则将惯导解算的过程融入到了状态空间模型的建立中，滤波和解算合二为一，从而简化了计算步骤。因此，在仿真实验中松组合直接法的运行速率约为间接法的2.5倍。

在实际应用下，丢星是不可避免的。在本实验中设置的包含丢星的场景下，直接法和间接法的水平位置均方根误差值分别控制在1.24 m和0.71 m以内，垂直位置均方根误差值控制在2.08 m和0.87 m。直接法中，INS随时间推移位置误差不断累积，当GPS信号丢失，只能依靠单纯INS导航，位置、速度误差迅速增加；间接法在丢失GPS信号后，不断利用上一时刻估计的误差递推，修正惯导，丢星时间又较短，估计出的误差与实际累积误差相近，故精度下降有限。

丢星场景下，直接法滤波不稳定，轨迹偏移最大可达20 m；间接法滤波相对稳定，轨迹的偏移很小。此外，在上升段丢星的5 s内，直接法滤波的位置误差和速度误差分别控制在8 m和5 m/s以内，间接法轨迹便偏移在3 m内，这是由于无人机处于匀速上升段，姿态、速度均保持不变，丢星后间接法基本不变，直接法有偏移但可控；在平飞段的5 s丢星，无人机正在转弯，姿态、速度不断地变化，直接法三维位置误差和速度误差最大均超过20 m和5 m/s，间接法此时误差略大于上升段，但在5 m内；在下降段的5 s丢星，无人机处于减速下降阶段，需要不断调整姿态来保持飞行，但由于速度较小，故误差与平飞段的5 s丢星相近，直接法的东向和北向位置误差控制在10 m内，速度误差控制在10 m/s内，间接法的误差基本保持不变。此外，由于直接法的滤波方程中包含了位置、速度、姿态等不同数量级的物理量，而在滤波过程中优先考虑了位置和速度，随着时间的推移，对于姿态的滤波逐渐发散，如图11所示；间接法主要针对各个误差量进行滤波，数量级相近，故整体滤波效果优于直接法。最后，松组合直接法对于速度和姿态的滤波效果远比间接法差，姿态变化对于直接法滤波影响较大，滤波后的姿态相对于间接法非常不稳定，且在丢星时速度误差急剧增大，进而带来定位精度的降低。

仿真结果表明，松组合直接滤波法和间接滤波法在不丢星情况下对于导航系统的精度提高相差不大。考虑丢星，松组合间接法在精度和稳定性方面均优于直接法，但在滤波计算速度方面直接法优于间接法。

3 实例验证

本文的试验数据采用2018年2月25日于台湾南投采集的无人机飞行数据，飞行时间约20 min。所用无人机和试验环境如图12所示，试验场地和飞行轨迹如图13所示，表9为组合导航系统中各传感器的相关参数设置。

本文分别使用组合导航直接法和间接法2种建模方式进行滤波，如图14和图15所示，其中，GPS位置信息为基于C/A码伪距解算定位的结果。2种组合方式下的组合导航系统状态运动位置误差、速度误差和姿态误差分别如图16～图18所示。

图12 所用无人机和试验环境Fig.12 UAV used and test environment

图13 试验场地与飞行轨迹鸟瞰图Fig.13 Test site and aerial view of flight path

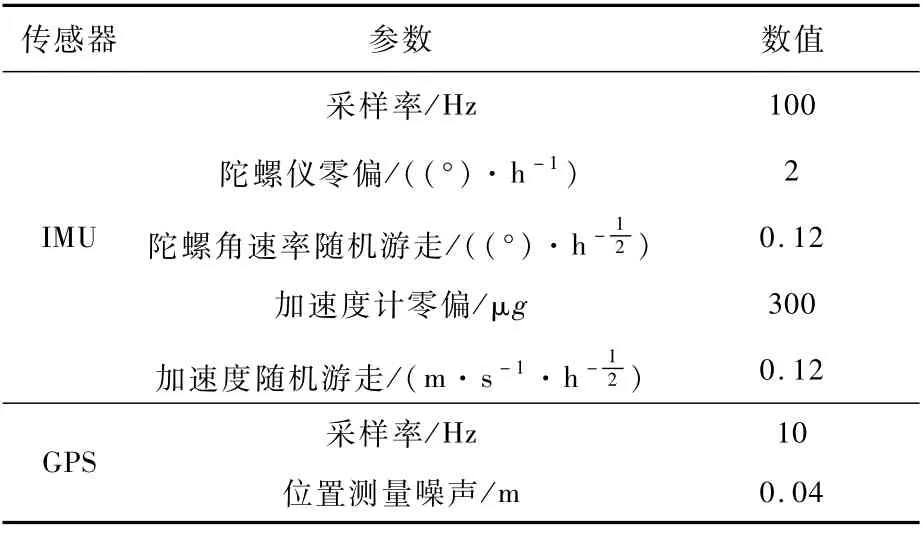
表9 组合导航系统测量精度Table 9 Measurement accuracy of integrated navigation system

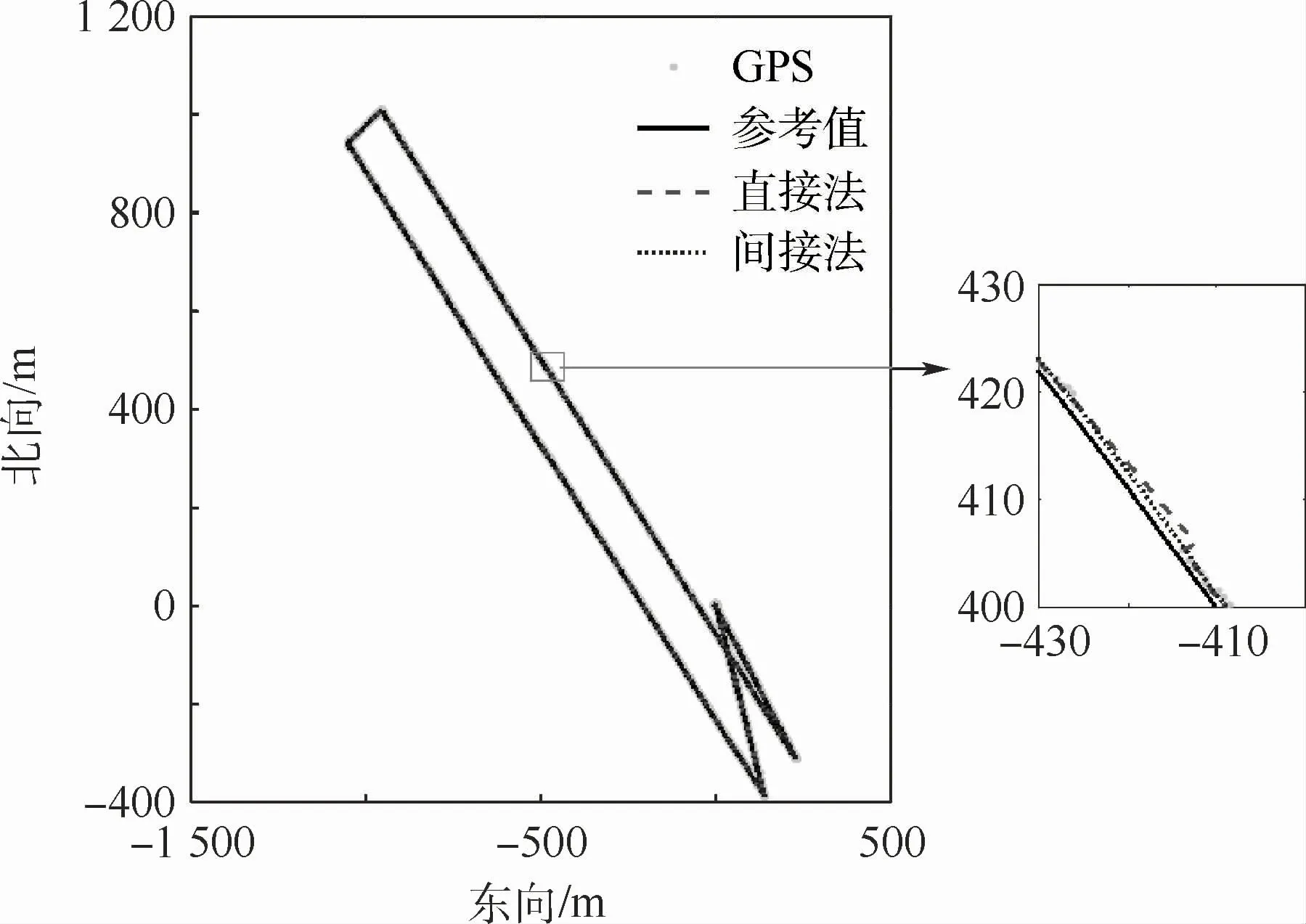
图14 试验飞行轨迹（水平维度）Fig.14 Test flight trajectory（horizontal dimension）

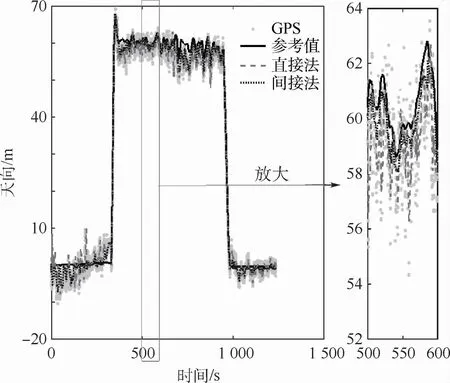
图15 试验飞行轨迹（竖直维度）Fig.15 Test flight trajectory（vertical dimension）

计算本试验中直接法、间接法和GPS的位置RMSE见表10。计算直接法和间接法的速度RMSE、姿态RMSE分别见表11、表12。直接法和间接法运行时间见表13。

图16 试验飞行轨迹的位置误差Fig.16 Position errors of test flight trajectory

图17 试验飞行轨迹的速度误差Fig.17 Velocity errors of test flight trajectory

图18 试验飞行轨迹的姿态误差Fig.18 Attitude errors of test flight trajectory

表10 直接法、间接法和GPS的位置RMSE（与Inertial Explorer相比）Table 10 Position RMSE of direct mode，indirect mode and GPS（compar ed to Iner tial Explor er）

表11 直接法和间接法的速度RMSETable 11 Velocity RMSE of direct mode and indirect mode

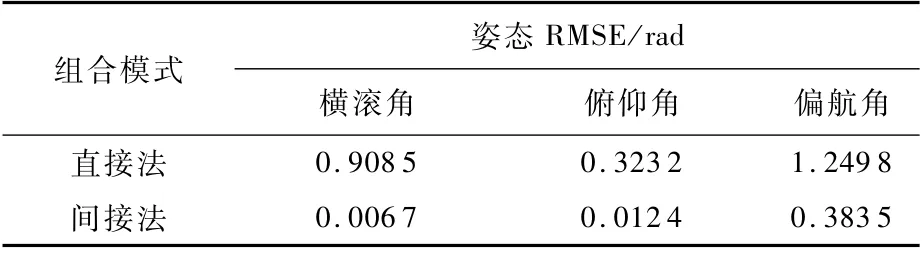
表12 直接法和间接法的姿态RMSETable 12 Attitude RMSE of direct mode and indirect mode

表13 直接法和间接法运行时间Table 13 Runtime of direct mode and indirect mode

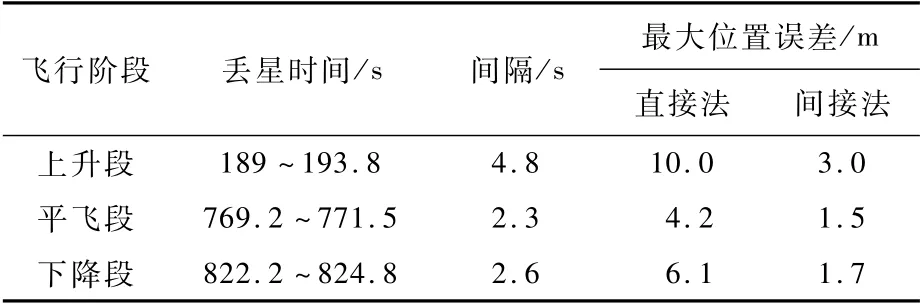
表14 各丢星部分最大位置误差Table 14 Maximum position error in lost-star parts

与仿真环境不同，无人机在实际飞行时，除了组合导航子系统的性能外，还受自身尺寸、性能、飞控系统等的影响。此外，外界复杂的气象条件和操纵人员的技术也对无人机的飞行具有一定的影响。本试验进行的实际环境中，受多种因素联合作用，无论是上升、平飞还是下降段，无人机的飞行状态一直处于高动态变化中，这一点可以从图14和图15直接看出，这些因素使得其真实位置、速度、姿态无规律波动，进一步加剧了直接法滤波的不稳定性，这是本试验中姿态发散相对于仿真环境下更快的原因。

试验结果表明，松组合直接滤波法和间接滤波法均能一定程度上提高导航系统的精度，且在精度和稳定性方面松组合间接法优于直接法，在滤波计算速度方面直接法优于间接法。这也进一步验证了仿真实验结果的合理性。

因此，直接法和间接法均能提高动态无人机的导航系统精度和稳定性，且间接法优于直接法，但间接法的滤波计算速率比直接法慢。

4 结 论

本文挖掘了高动态无人机导航中的状态估计问题，分析了GNSS/INS的组合导航系统在无人机中的应用，针对2种主要组合方式——直接法和间接法，分别设计了基于EKF的松组合导航算法。主要结论如下：

1）试验表明，理想的不丢星场景下，直接法和间接法的精度相当。真实情况中不可避免存在丢星问题，此时间接法在精度和稳定性方面优于直接法，且丢星情况越严重，间接法的优势越明显；而直接法在滤波计算速率方面优于间接法。

2）目前，系统计算性能的提升可以有效解决计算效率的问题。因此，在面向高精度、高可靠性需求的无人机应用中，建议选择间接法作为无人机导航的技术方案。针对精度要求不高、可靠性要求较低的应用，选择直接法作为无人机导航的技术方案可以在一定程度上降低系统的成本。

在未来的研究中，将进一步分析紧组合情况下的直接法和间接法的性能以及它们在不同场景下的无人机导航中的应用。