密封汽流激振下转子动力特性的时域分析

司和勇，曹丽华，*，郭帅，李盼

（1.东北电力大学 能源与动力工程学院，吉林132012； 2.吉林省电力科学研究院有限公司，长春130021）

高参数的蒸汽在汽轮机中流动受不均匀间隙的影响会对转子产生较大的压力偏差，进而产生汽流激振力，影响转子的稳定运行。Alford［1］对汽流激振力分析得出，当转子受力不平衡时会发生偏心，偏心后所形成不均的圆周间隙使得汽流对转子作用力不平衡，继续促使转子做偏心运动。为揭示汽流激振力的形成机理，许多学者采用了不同的密封计算模型进行研究［2-6］，转子汽流激振力计算模型也越来越完善。许多国内外学者通过CFD软件对转子的汽流激振力做出研究，结果表明影响汽流激振力的因素并不唯一［7-8］。丁学俊和Rhode［9-10］等对静偏心模型进行稳态计算发现，偏心距的增大使转子汽流激振力增加；而动力特性系数与偏心率呈非线性关系，随着进出口压差增大，转子的交叉刚度朝负方向增加而直接阻尼减小。随着入口正向预旋的增加，交叉刚度由负值逐渐增加到正值，使转子系统不稳定［11］。孙丹等［12］发现适宜的反向预旋有利于转子的稳定。基于该理论，由von Pragenau［13］提出的阻尼密封能够减少汽流在密封腔内的周向运动，从而减少周向运动导致的转子受力不平衡，降低了交叉刚度，提高转子稳定性。一些外国学者通过相对坐标系的方法模拟了转子涡动模型，并将不同软件的计算结果对比，结果表明，CFX-TASCflow可以较准确地计算转子动力系数［14］。Subramanian等［15］在考虑离心作用对径向力和切向力的影响后，认为在低转速时离心作用的增强导致径向力减小，这种影响随压比的增加更加明显，而切向力几乎不变。随着转速的升高，离心作用会使径向力和切向力在低压比条件下发生突变。Ma等［16］发现分岔转速随密封直径和长度的增加而增大。对于动力系数的求解，一般采用傅里叶变换，在频域上分析其变化特性，但动力系数的时域变化却少有人分析。

目前研究中多采用静偏心模型或相对坐标系模拟转子涡动，但该模型无法准确实现转子涡动，同时频域上的动力系数特性难以反映转子稳定性随时长的变化。为改善上述不足，本文基于隔板汽封结构建立三维转子计算模型，采用Fluent动网格技术对转子涡动进行真实模拟，并提出动力系数的时间差分求解方法。分别考虑转子转速、涡动半径、涡动速度等因素对转子动力特性的影响，求解转子的径向力和切向力，同时对交叉刚度、直接刚度、交叉阻尼、直接阻尼等动力系数进行深入的研究。

1 计算模型

1.1 建立物理模型

以某300 MW 汽轮机组高压缸第二级隔板汽封为例，建立三维全周转子涡动模型。采用ANSYSICEM划分非结构网格，基于Fluent压力求解器计算隔板汽封内部非稳态流场。具体结构参数如图1所示，设密封齿腔深为h、齿厚为t、凸台高度为d、密封齿顶间隙为Cr，偏心距为e，以偏心率η=e/Cr表示转子的偏心程度。以机组额定工况为基准，设定压力入口为10.7 MPa，温度为744.25K；压力出口为10.263 MPa，温度为734.25 K。结合标准的k-ε方程和SIMPLE算法三维求解迷宫密封流场的Navier-Stokes方程。采用动网格计算时，在保证初始网格质量合格的同时还要采用较好的网格更新技术，在静偏心下验证初始网格如图2所示，当网格数量达到400×104时，对模型的计算结果无影响。构建转子涡动模型如图3所示，假设径向力Fr以大间隙指向小间隙为正，切向力Ft以逆时针方向为正。

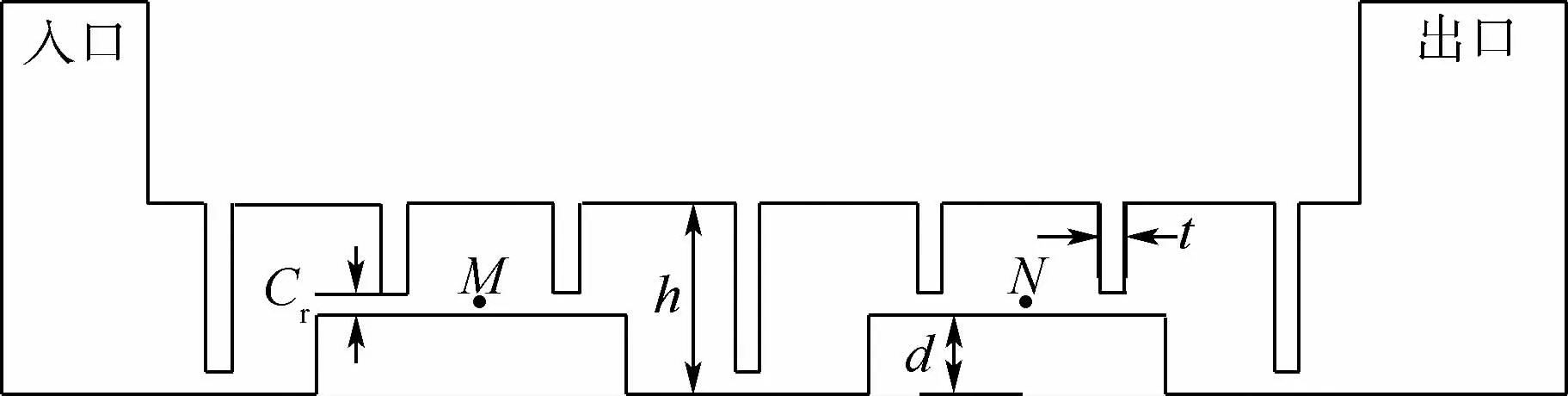
图1 迷宫密封结构参数Fig.1 Parameters of labyrinth seal structure

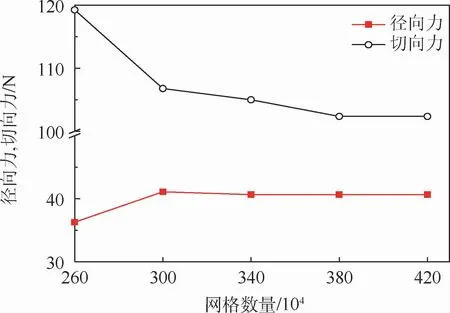
图2 网格数量对计算结果的影响Fig.2 Influence of grid quantity on calculation results

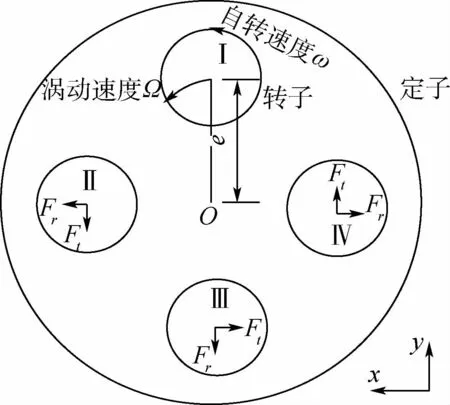
图3 转子涡动模型示意图Fig.3 Sketch map of rotor whirling motion model

1.2 动网格技术

在模拟转子真实的涡动时，由于转子是以刚体形式涡动从而使隔板汽封径向间隙不断发生变化，需要使物理模型中的转子按照定义的运动规律进行涡动，而这种运动会导致模型的边界发生改变。考虑到动网格可以定义边界的运动形式，以实现流体域因边界运动而变形的非稳态计算。模型采用用户自定义函数UDF实现三维转子涡动。湍流模型、涡动方程及网格验证部分详见文献［17］。

1.3 转子动力系数的时域计算

式（2）、式（3）所组成的方程组中含有4个未知数，若要求得固定解还需2个方程。本文中以时间为变量，假设转子做圆形的偏心涡动，将转子中心在定子内圆周方向选取均匀分布的8个点作为转子运动的监测点，其中4个位置如图3所示。与每个监测点相邻的上一时间步长和下一时间步长的转子运动状态也在研究范围之内，因此在任意一个监测点均可建立四元一次方程组，如下：

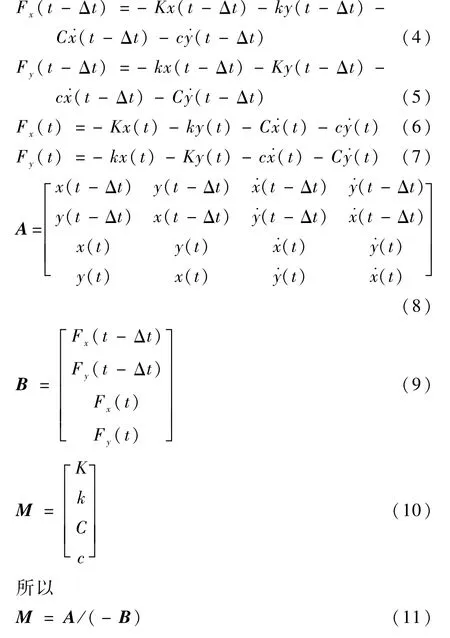
通过计算求解矩阵可求得动力特性系数的实数解。为保证计算结果的准确性，排除时间步长交叉对转子动力特性的影响，流场计算和差分求解的时间步长均为10-4s，即在时间上是点对点嵌合的。

2 数值模拟结果及分析

首先对间隙Cr为0.5 mm、η=10%的计算模型进行求解。在考虑机组长期运行过程中的磨损问题后，又对间隙Cr为1 mm、η=10%的模型进行计算。比较二者的径向力与切向力的变化趋势，可以发现在间隙Cr为1 mm时，转子的汽流激振力变化较为明显，如图4所示。为充分研究转子动力系数的变化特性，先以无偏心时隔板汽封间隙为1 mm、涡动速度为转子半转速即1 500 r/min为例，分别对偏心率η为10%、20%、30%、40%和50%的工况进行计算。

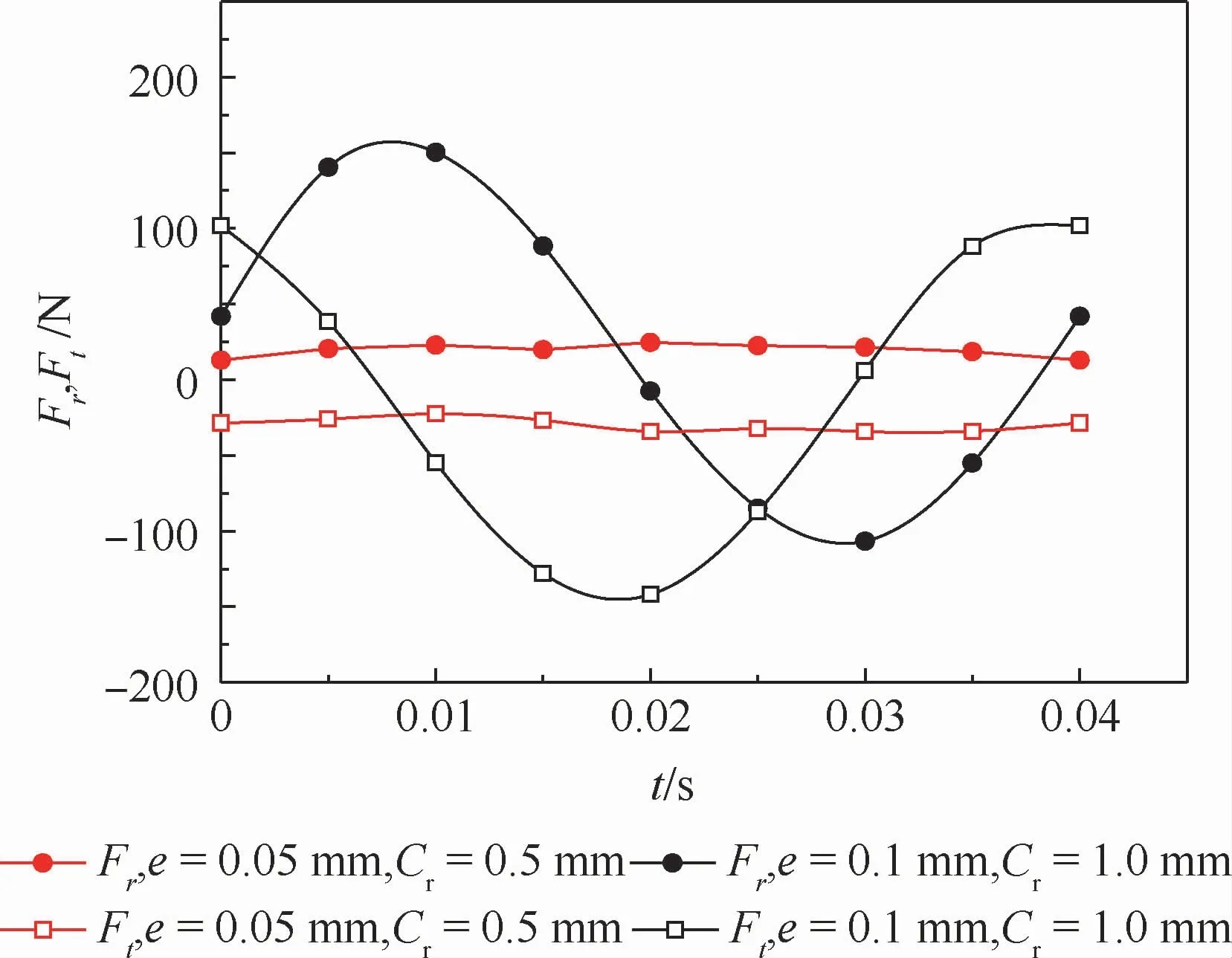
图4 偏心率为10%下不同间隙的汽流激振力变化Fig.4 Steam flow excited vibration force in different clearance under 10% eccentricity

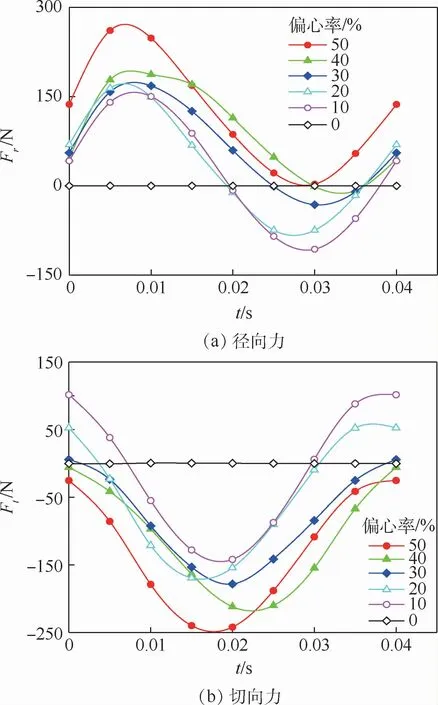
图5 不同偏心率下转子汽流激振力Fig.5 Rotor steam flow excited vibration force under different eccentricity

当间隙为1 mm、涡动速度为1 500 r/min时，得到径向力Fr和切向力Ft在转子涡动一周的过程中变化趋势如图5所示。转子的径向力Fr呈正弦曲线变化，切向力Ft呈余弦变化。两者在不同偏心距下涡动会存在不同的变化范围。由于大偏心下蒸汽的动压效应较强，蒸汽受压缩和膨胀的程度加剧，对转子作用较强，所以最大径向力和最大切向力的绝对值均出现在偏心率最大时的工况即η=50%。观察相同时间点的不同间隙下的汽流激振力可以发现，转子的径向力与切向力并不是严格地随着偏心的增加而增大。随着偏心距的增加，径向力向正方向增加，而切向力向负方向增加，即二者在图中总体分别呈上升和下降趋势。将二者对时间平均化，得出η每增加10%，径向力与切向力会增加约25～35 N。但在某一时间段内也会存在小间隙的汽流激振力大于大间隙下的汽流激振力。这是由于转子在涡动过程中会对流场产生附加的扰动，而这些扰动对转子产生不稳定的附加力，导致转子受力出现波动。在静偏心或相对坐标系的模型中，只能研究转子位于位置Ⅰ的工况，所以将非定常转子涡动模型简化为定常模型来计算是不完全准确的，因为定常计算中无法考虑转子涡动带来的附加影响。从图5（a）中还可以看出，在偏心率小于50%时，转子的切向力既有正值也有负值，由于在1.1节的叙述中已规定切向力的方向，这表明在涡动过程中径向力的方向是变化的，并不是只由小间隙指向大间隙或由大间隙指向小间隙。再一次表明定常计算转子涡动模型具有片面性。

通过对转子圆周上监测点的数据处理得到转子的动力系数，如图6所示。在一个运动周期内，直接刚度K呈正弦曲线变化；交叉刚度k与直接阻尼C近似呈余弦变化；而交叉阻尼c近似为正弦变化。在密封间隙和涡动速度不变的条件下，转子的偏心距越大，其动力特性系数变化范围越小。偏心率在10% ～20%时，转子动力特性系数变化较偏心率在30% ～50%范围内变化更为突出。偏心率为30%、40%、50%三者的动力特性曲线变化规律较差是因为超过20%的偏心率不满足小扰动线性理论，会产生较大的误差。而偏心率增大导致动力系数值的减小，则是由于偏心率增加时，位移与速度呈增加，但汽流激振力呈非线性增加，即汽流激振力增加的量要比速度和位移的增加量少。

在判别转子系统是否稳定时，要考虑转子动力系数的变化趋势。由图5可以发现，最大径向力Fr出现在0.01 s时刻左右，对应图3中的位置Ⅱ，此时Fr与Fx（t）相等，x（t）与˙y（t）达到最大值而y（t）与˙x（t）为零，通过式（2）分析可知，Fx（t）即径向力Fr的增大使转子系统产生较大的直接刚度；而最大切向力出现在0.02 s附近，对应图3中的位置Ⅲ，此时Ft=-Fx（t），x（t）为零，-y（t）为最大值，˙x（t）最大值，˙y（t）为零，同样参考式（2）发现，切向力Ft的增大使转子系统产生较大的交叉刚度。表明较大的径向力和切向力都能导致系统的不稳定，而当转子的位置不同时，引起失稳的主要汽流激振力也不同，径向力与切向力交替着起主导作用。

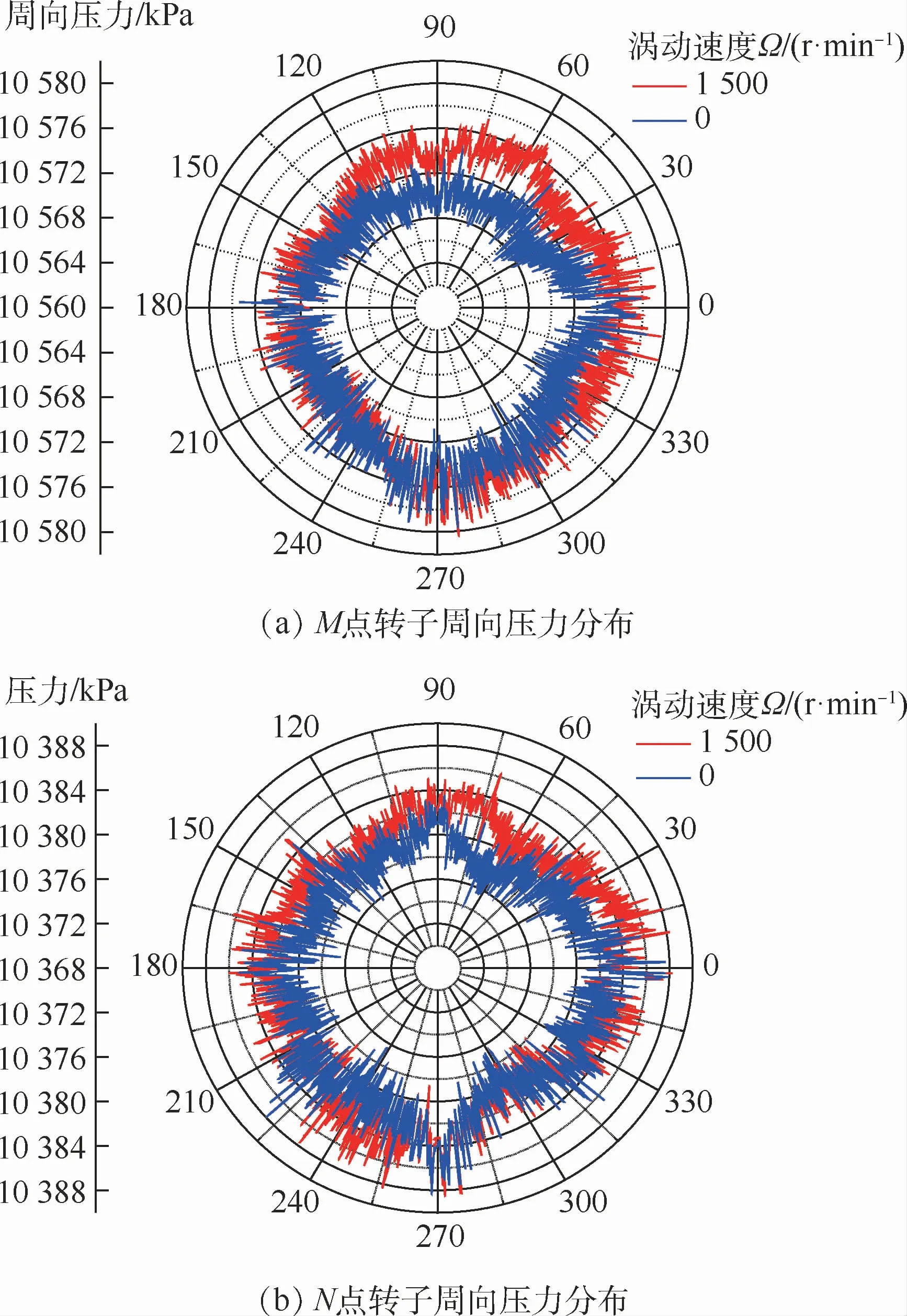
图7 不同涡动速度下转子周向压力分布Fig.7 Rotor circumferential pressure distribution under different whirling speeds

图7为间隙为1 mm，偏心率为10%时动偏心和静偏心的转子周向压力分布。参考图1中M、N两点，绕该两点作转子周向环线，得到转子表面的压力线。当转子在图3所示的位置Ⅰ时，对比二者的周向压力分布可以发现，转子表面的压力在一定范围内呈跳跃式分布，并非按照某一趋势平滑变化。动偏心时的压力线略高于静偏心的压力线，总平均压力相差1.5～2 k Pa。二者的变化曲线存在部分交叉，而非交叉部分则是由于转子涡动导致流场变化而引起的附加压力。尤其是在0～90°范围内，动偏心的压力明显高于静偏心，使得压力分布具有更高的非对称性。说明由涡动产生的附加压力具有不可忽略的作用。而且在M点的压力波动差要高于N点的压力波动。因此，转子在实际的涡动中，压力不均匀分布不仅受间隙不均的影响，还受涡动时流场变化的影响，从而导致汽流激振力的非线性变化；高压区因涡动引起的压力波动要比低压区的明显。这也解释了随着机组的参数越高，汽流激振力越大、越不稳定。

涡动速度不同时，转子运动一周的时间也不同，设时间比Φ=t/T，T为转子涡动一个周期的时间。当时间比Φ 相等时，任何涡动速度下的转子位置是相同的，以此建立图8来研究涡动速度对汽流激振力和转子稳定性的影响。观察图8（b），对比Ω在375～3 000 r/min的Ft变化曲线可知，在0时刻切向力随涡动速度的增加而减小（绝对值增大），该变化趋势与静偏心模型结论相同。而在整个时间域内，涡动速度差值较小的切向力依旧存在交叉，即切向力的增加不是严格的随涡动速度的增加而增加。只有涡动速度相差较大时，切向力变化越明显。对比图8（a）中的375 r/min和6 000 r/min发现，径向力Fr随涡动速度的增加变化很小。对比图8（a）、（b）可知，切向力随涡动速度变化的趋势要高于径向力。因此，涡动速度对汽流激振力的影响主要表现为使切向力发生变化，而对径向力影响较小。对涡动速度变化时的动力系数求解发现，直接刚度K和交叉刚度k基本不变化，在此未做展示；而直接阻尼C依旧呈余弦变化，且随着涡动速度的增加而减小，但正值所占据的范围在时间上有所增加。交叉阻尼呈正弦变化，其变化范围同样随涡动速度的增加而减小。

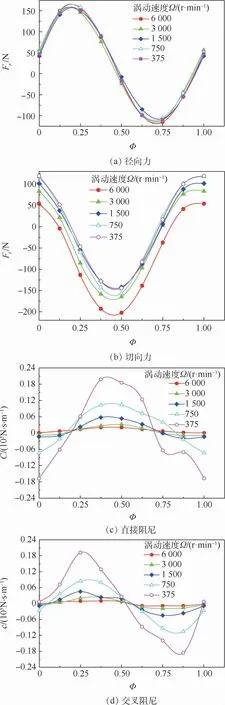
图8 涡动速度对汽流激振力和动力系数的影响Fig.8 Influence of whirling speed on steam flow excited vibration force and dynamic coefficients

涡动速度变化对流场特性有一定影响，取图3中位置Ⅰ的模型，过M 点建立隔板汽封轴向和径向的垂直交叉面，分别作流场迹线图和湍动能云图，如图9所示。随着涡动速度的增加，密封内湍动能的分布变化较小，但在密封齿顶出现较大的湍动能，这表明在涡动速度变化的过程中，蒸汽的动能耗散仍是密封作用的机理。不考虑入、出口边界条件的影响，中间齿的齿顶湍动能分布随涡动速度的增加而增加。涡动的增强使迹线变得紊乱，在涡动速度为3 000 r/min时迹线整齐的斜向延伸，这是由于自转速度与涡动速度相同，引起蒸汽的同步运动，加剧了对蒸汽的携带作用。而在涡动速度为6 000 r/min时，迹线又恢复到近似375 r/min的状态，表明自转与公转超出了彼此影响的频率。但涡动速度为6 000 r/min时，迹线在转子近壁面处的汇合层向上偏移，即迹线掺混位置远离了转子壁面。这是由于较大的涡动速度使转子壁面的绝对速度增加而引起的。

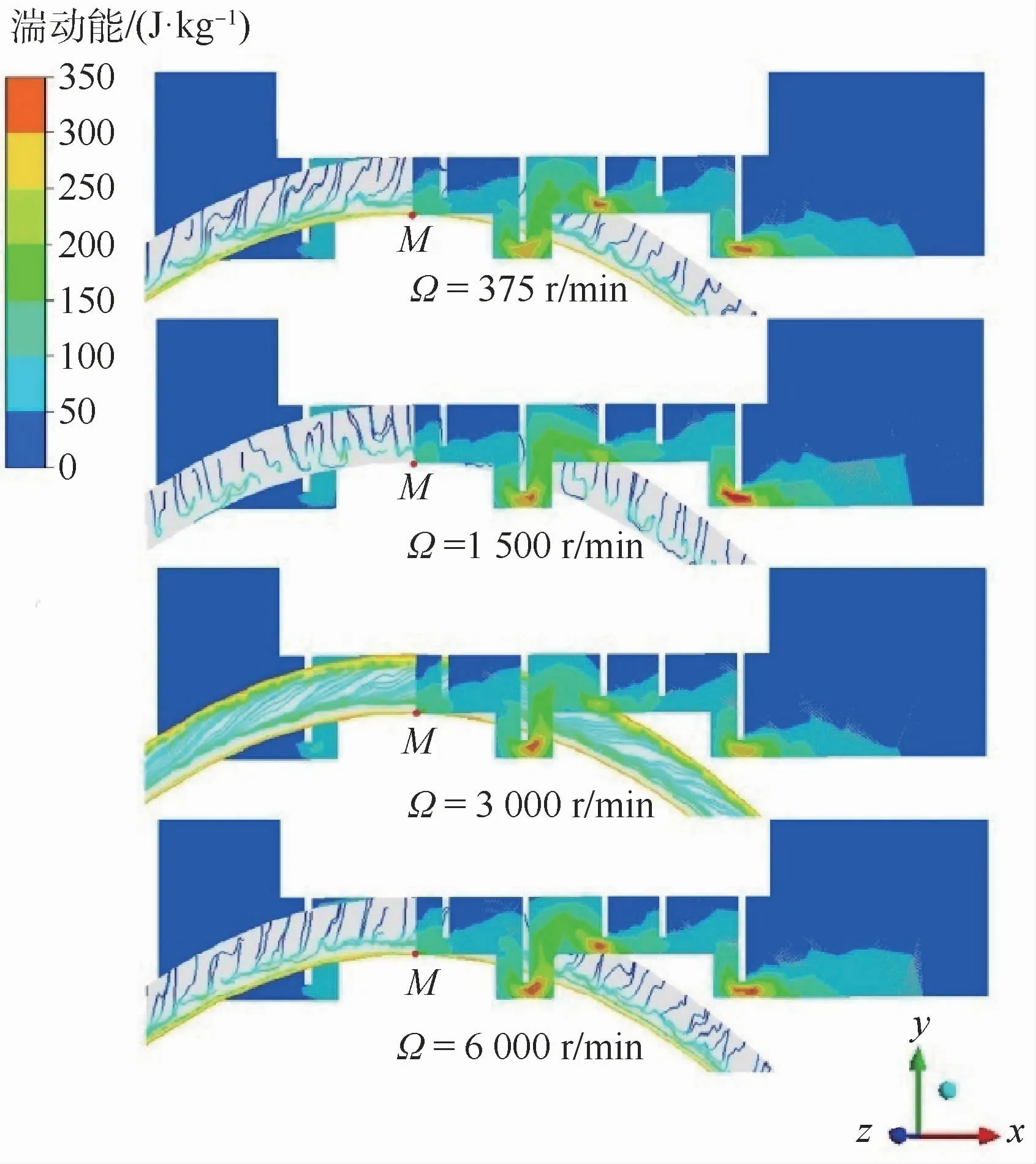
图9 流场迹线与湍动能云图Fig.9 Streamlines and turbulent kinetic energy contours of flow field

图10为转子涡动速度为1 500 r/min，在不同自转速度下测得的汽流激振力变化及求解的动力系数。可以发现，在375～3 000 r/min范围内，汽流激振力随转速变化较小。在0.01 s和0.03s时，径向力有明显的变化，在0.02 s和0.04 s时，切向力有明显的变化，而在其他时刻转子受力曲线几乎重合。其原因是转子涡动过程中转子位置发生变化，由偏心位置变化引起汽流激振力的变化起主导作用，当涡动速度不变，转子涡动规律相同，汽流激振力总体按某一规律变化。当转子位置只存在单方向变化时，即只在x或y方向存在位移和速度时，由自转引起的汽流激振力变化才显现出来；且随着转子自转速度的增加，汽流激振力的最大值逐渐减小。

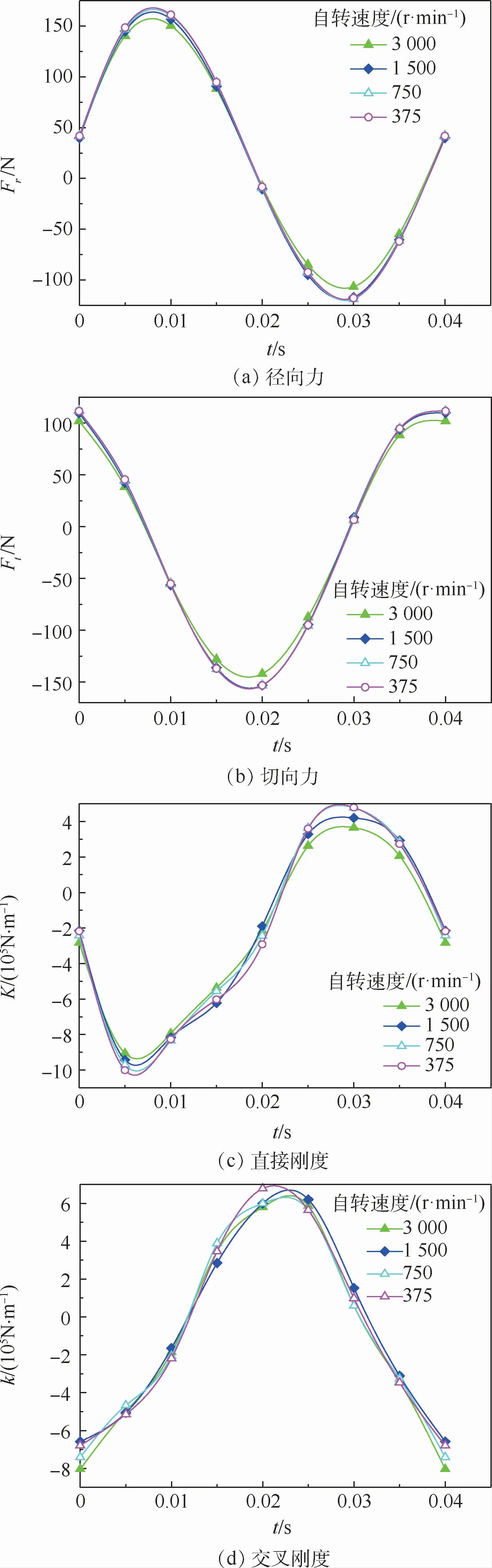
图10 自转速度对汽流激振力和动力系数的影响Fig.10 Influence of rotational speed on steam flow excited vibration force and dynamic coefficients

观察直接刚度K和交叉刚度k，在0.01 s和0.03 s时，直接刚度发生明显变化，其绝对值随着自转速度的升高而减小，与径向力变化一致；在0.02 s和0.04 s时，交叉刚度略有变化，随自转速度的升高有减小的趋势。0.02 s时切向力为负，其绝对值的减小使得交叉刚度减小，0.04 s时切向力为正，其数值的减小导致交叉刚度的负向增加。因此，在0.04 s（即图3中位置Ⅰ）时，交叉刚度的负向增长不利于转子稳定。

图11为以间隙1 mm，偏心率10%，涡动速度1 500 r/min工况下改变进出口压比得到的汽流激振力变化特性曲线。可以看出，径向力随压比的增大，朝正方向增加；切向力随压比的增大而减小，即朝负方向增加。上述变化均导致最大径向力和最大切向力的绝对值增加。而对转子动力系数研究发现，4项系数均无明显的变化规律，换言之，压比的增加使转子周围整体的流场发生变化，对所有的转子动力系数均有影响，但该影响在时域上是无规律的、杂乱的。

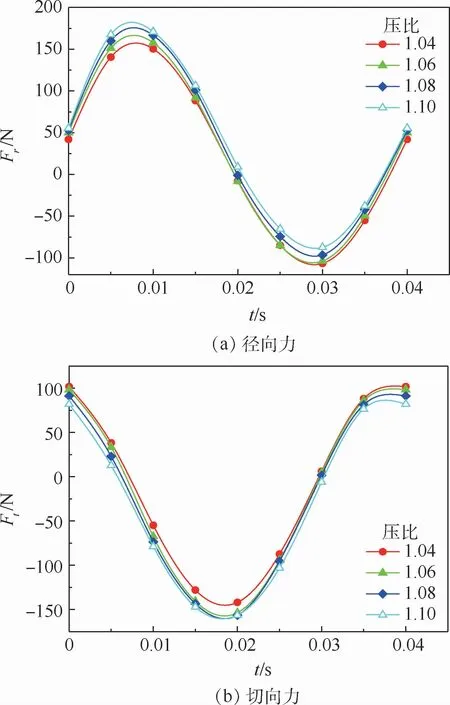
图11 汽流激振力随压比的变化趋势Fig.11 Change of steam flow excited vibration force with pressure ratio

3 结 论

1）当转子以圆形轨迹涡动时，汽流激振力随着转子中心位置的改变而变化。其径向力随时间呈正弦变化，切向力为余弦变化，二者均随偏心率的增加而增加。额定工况下，偏心率每增加10%，汽流激振力的平均值升高25～35 N。当偏心率小于50%时，径向力Fr在前半周期由大间隙指向小间隙，后半周期由小间隙指向大间隙。

2）直接刚度K近似为负正弦曲线，交叉刚度k与直接阻尼C近似为余弦，交叉阻尼c近似为正弦。当转子处于不同位置时，引起转子失稳的主要汽流激振力也不同，径向力与切向力交替成为引起转子失稳的主要原因。

3）涡动速度的增加对径向力影响较小，而对切向力影响较大。随着涡动速度的增加，切向力的绝对值增大，直接阻尼和交叉阻尼均减小，转子趋于不稳定状态。在一定的自转范围内，随着转子自转速度的增加，汽流激振力的最大值有较小的降低趋势。压比的增加导致径向力增大而切向力减小。