基于速度锁定器的桥梁抗震数值模拟方法及验证

李明鹏，赵凌冬

(重庆万桥交通科技发展有限公司，重庆 401336)

速度锁定器LUD(Lock-up Device)是液体粘滞阻尼器的一种特殊形式，二者有着相似的缸体结构及力学模型，但其工作原理与粘滞阻尼器不同[1]。粘滞阻尼器在有限元软件中一般采用Maxwell模型来模拟，但在有限元软件中采用Maxwell模型模拟速度锁定器鲜有报道。

速度锁定器是一种被动减震设备，是速度相关型锁定设备，在桥梁工程设计软件Midas Civil中尚没有模拟速度锁定器的功能[2]。目前，国内外学者对粘滞阻尼器和速度锁定器从多方面开展了研究工作。余小华等[3]提出在Midas Civil中采用粘滞阻尼器、弹性约束(一般)和弹性约束(折线型)等3种简化方式来模拟速度锁定器。郑晓龙等[4]对速度锁定支座进行了锁定性能测试并分析了其减震性能。刘恒龙等[5]基于Matlab建立了速度锁定器结构仿真模型并进行了动态特性测试。颜志华等[6]从设计参数选取和减震效果研究了速度锁定器在减震设计中的应用。Douglas P. Taylor[7]详细阐述了速度锁定器的工作原理并介绍了该设备在悉尼大桥上的应用。Warren M. Brown[8]介绍了速度锁定器在桥梁上的设计、安装和操作。Liang Jie[9]介绍了锁定器空隙参数的设计及其对慢速移动试验、快速移动试验和模拟动态试验的影响。蒋建军等[10]研究了在梁端设置非线性粘滞阻尼器，可减小大跨径连续刚构桥的顺桥向地震力和位移。综上可知，已有研究主要针对速度锁定器减震设计、性能试验及减震效果方面，但是对有限元模拟中参数如何选取未作出详细研究。

本文基于桥梁工程有限元软件Midas Civil，采用Maxwell模型构建速度锁定器恢复力模型，对速度锁定器的参数取值进行研究，通过算例对比理论解析解与数值模拟结果，验证参数模拟的可靠性。

1 LUD动力测试模拟

1.1 Maxwell模型

Midas Civil中边界非线性主要指结构中考虑附加的阻尼器和隔振器等装置的非线性属性，这类结构的单元不仅表现为非线性的属性，还可通过滞回曲线的定义考虑单元往复加载过程中的塑性发展和能量损耗特性。在一般连接中程序提供了多种边界条件模拟，粘弹性消能器同时拥有粘性和弹性，Midas Civil中提供了几种具有代表性的粘弹性消能器数学模型：Maxwell模型、Kelvin模型及Damper Brace Assembly模型[11]。

速度锁定器表现出强烈的频率依赖性，在Midas Civil中可用Maxwell模型的“阻尼器-刚度连续变化模型”来模拟，该模型中阻尼单元与弹簧单元串联[8]，如图1所示。

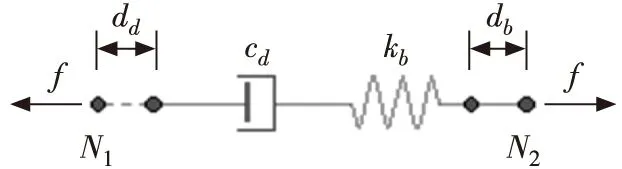
图1 Maxwell模型示意

Maxwell模型计算公式[12-15]可表示为：

(1)

d=dd+db

(2)

式中：Cd为消能器阻尼，kN；V0为参考速度，mm/s；s为速度指数，为常数；kb为连接弹簧刚度，kN/mm。

等效刚度kb可由下式确定：

kb=9F/D

(3)

kb=F/d

(4)

式中：F为速度锁定器承载力，kN；D为支座配套的位移，mm；d为速度锁定器锁定位移，mm。等效刚度kb取公式(3)和(4)计算的较大值。

1.2 有限元模型

采用有限元软件Midas Civil对速度锁定器动力测试进行模拟，如图2所示。速度锁定器2个节点采用一般连接的Maxwell模型，其中一个节点施以往复动力荷载，另一节点固定，荷载时间曲线与动力测试实际数据完全一致。

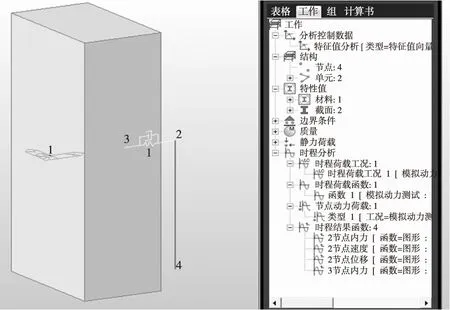
图2 动力测试模拟有限元模型

实验室中将速度锁定器一端固定于反力墙，另一端施以往复荷载。有限元中节点3固定，节点2施加节点动力荷载，节点2、3之间施加速度锁定器，边界条件采用Maxwell一般连接。实验室测得的速度锁定器承载力为1 000 kN，在Maxwell模型中结合公式(1)～(4)并多次试算，确定消能器阻尼Cd=1 000 kN，参考速度V0=1 mm/s，阻尼指数s=2，连接弹簧刚度根据公式(3)和(4)取两者之间的较大值kb=90 kN/mm,通过实验室试验数据和数值模拟结果对比来验证参数取值的正确性。

2 结果处理

实际动力测试下速度锁定器的出力及时间如图3所示，速度锁定器最大出力为1 000 kN。在Midas Civil 中通过节点动力时程施加同样的荷载-时间曲线，荷载周期4 s，加载时间10个循环共40 s，最大荷载为1 000 kN。

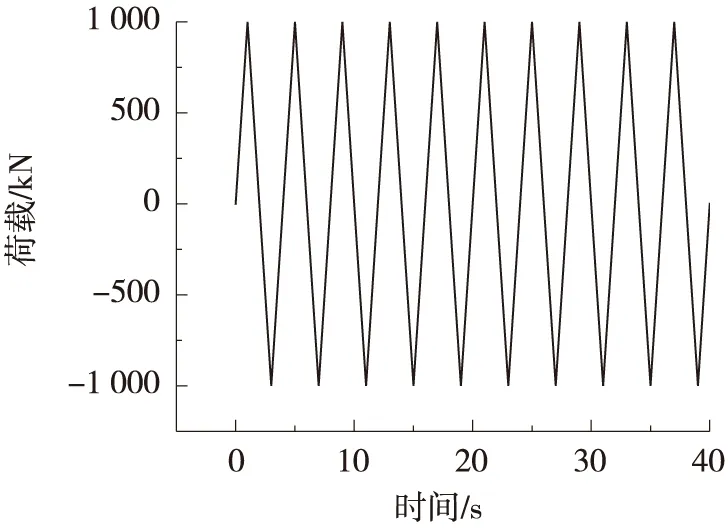
图3 荷载-时间曲线

速度锁定器力学模型中，锁定位移不大于12 mm。在Maxwell模型中对Cd、V0、kb值进行多次试算使锁定位移小于12 mm，并且数值模拟得出的滞回曲线与试验数据接近。数值模拟得出的节点2的位移随时间变化曲线如图4所示。由图4可知，锁定器锁定位移为11 mm，位移-时间曲线与动力测试荷载-时间曲线规律一致。速度锁定器实测及有限元分析的滞回曲线如图5所示。由图5可知，二者曲线很大程度上吻合，结合数值模拟与试验数据，一定程度上说明了速度锁定器采用该组Maxwell参数具有可靠性。

图4 节点2位移-时间曲线

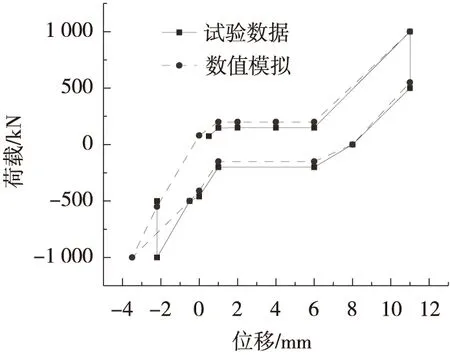
图5 节点2滞回曲线与试验数据曲线

3 实例验证

参照《桥梁抗震》第二版[16]某城市高架桥中的一联连续梁桥(3×22 m)为例进行验证，桥墩类型为实心矩形墩，墩高为11.7 m。主墩从左向右编号为1#、2#、3#、4#，其中2#墩为固定墩，1#、3#、4#为纵向活动墩，连续梁桥抗震计算有限元模型如图6所示。初步建立模型后，使得在1联3跨主梁恒载和二期恒载作用下，中墩和边墩支座反力与理论计算值完全一致。

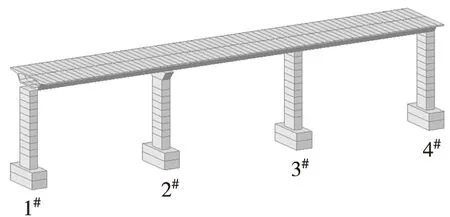
图6 3×22 m连续梁桥有限元模型

3.1 无速度锁定器工况

理论计算将连续梁在地震作用下的运动简化为单自由度模型，其质量中心位于固定墩支座顶部。对单自由度模型，在纵桥向E1地震和E2地震作用下，由反应谱法计算得到各个主墩墩顶的地震力和墩底弯矩，如表1所示。有限元模拟通过输入相应的地震加速度反应谱函数，得到连续梁各个主墩在E1地震和E2地震作用下的分析结果，如图7所示。

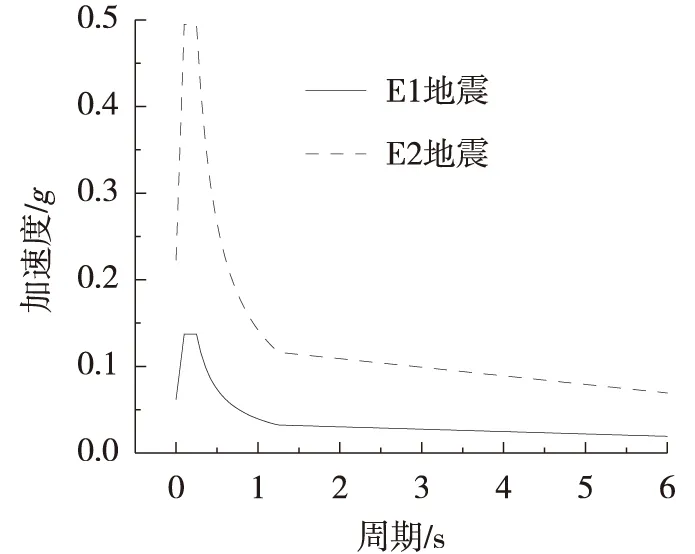
图7 E1、E2加速度反应谱

为减小地震动随机性导致的误差，理论计算采用的地震加速度反应谱与数值分析输入的加速度时程数据峰值加速度应接近。由表1可知，在E1地震和E2地震下，理论计算的连续梁桥周期、固定墩墩顶剪力、固定墩墩底弯矩较数值分析结果小，但总体上较相近且规律一致。这说明有限元模型可靠，可为施加速度锁定器工况模拟提供基础。

表1 3×22 m连续梁桥理论抗震计算与数值模拟结果

3.2 施加速度锁定器工况

分别在活动墩1#、3#、4#墩顶和主梁下部建立一般连接Maxwell模型，一般连接参数取值采用已验证的4个参数值。为减小地震波随机性的影响，采取3条罕遇地震波进行分析，罕遇地震下时程数据如图8所示。罕遇地震工况下，通过有限元分析得出1#～4#墩在设有速度锁定器下的墩顶剪力及墩底弯矩，并对比理论计算结果与数值分析结果。

E2地震工况下，速度锁定器瞬间锁定，最大出力达到设计值1 000 kN，此时活动墩1#、3#、4#在墩顶纵桥向相当于被刚性连杆连接，1#、3#、4#墩将与固定墩共同承受地震力，固定墩墩顶剪力和墩底弯矩将大幅度减小，活动墩承受剪力和弯矩增加，结果如表2所示。

图8 罕遇地震工况加速度时程数据

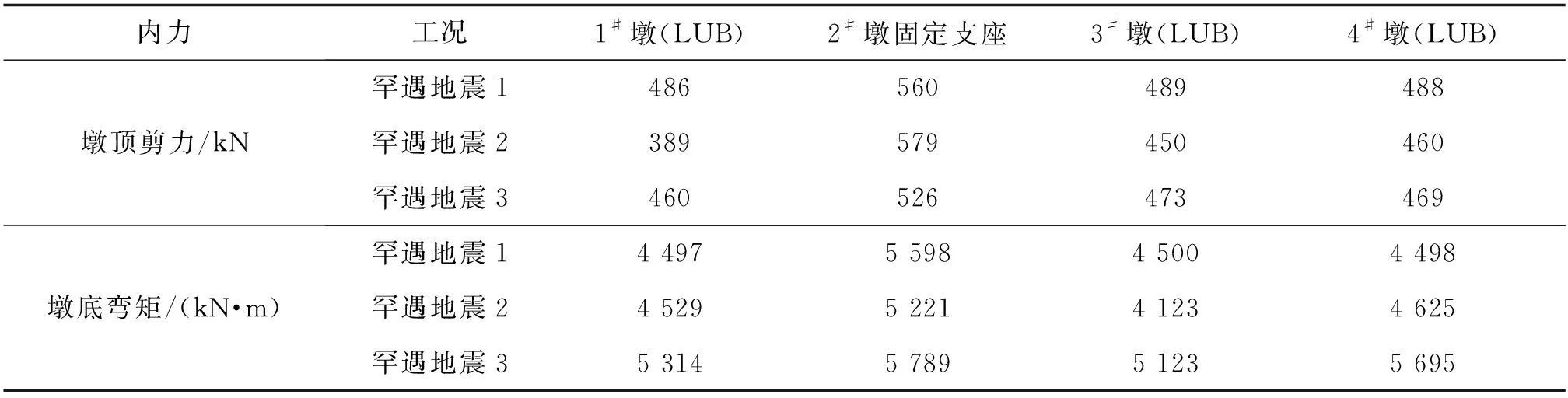
表2 安装速度锁定器后各墩最大内力

从前文分析可知，在罕遇地震下，速度锁定器发挥作用，锁定位移11 mm，最大出力1 000 kN；锁定后，2#固定墩墩顶剪力从理论1 612 kN减小到560 kN，墩底弯矩从理论18 900 kN·m减小到5 598 kN·m，活动墩锁定后变为固定墩共同受力，墩顶剪力由0增加到488 kN，活动墩墩底弯矩比固定墩的略小，通过连续梁桥地震作用下理论计算与数值分析，得出在有限元软件中采用Maxwell模型的参数模拟是可靠的。

4 结论

1) 速度锁定器在有限元软件Midas Civil中模拟时，可保守采用粘滞阻尼器来模拟，但用Maxwell模拟时相关参数应多次试算调整，其中弹簧连接刚度取值可以参照公式(4)，当模拟结果不够理想时，弹簧连接刚度取值可对公式(4)计算值微调。

2) 采用有限元软件模拟速度锁定器的动力测试，数值模拟结果与实测结果对比分析验证了Maxwell模型对速度锁定器参数取值具有一定的可靠性，对比结果显示速度锁定器最大位移11 mm，最大出力达1 000 kN，且试验和数值模拟得出的滞回曲线吻合。

3) 速度锁定器属于特殊的粘滞阻尼器，相同点是两者的力学模型基本相似，都是速度相关型，在有限元软件中均可采用Maxwell模型来模拟。不同点是速度锁定器由于在极小的速度下发生瞬间锁定，整个过程不发生能量的耗散，而粘滞阻尼器主要通过耗散地震能量来达到减震效果，二者的减震机理不同，本文通过实际算例验证了连续梁桥采用速度锁定器能达到良好的减震效果。