数控车削宏程序编程规律分析及应用

张 琳

数控车削宏程序编程规律分析及应用

张 琳

（沙洲职业工学院，江苏 张家港 215600）

从数控车削宏程序编程步骤入手，分析数控车削宏程序编程的方法和规律，总结出了较为通用的编程模板，为初学者提供借鉴和参考，可以使初学者较为快速地学习和掌握数控车削宏程序编程技巧。

数控车削；宏程序；编程模板

引言

随着现代制造技术的发展，数控加工技术在我国得到了广泛的应用，应用宏程序对可以用函数公式描述的工件轮廓或曲面进行数控加工，是现代数控系统一个重要的新功能和方法。然而在使用宏程序编程用于数控加工公式曲线时，需要具有一定的数学和高级语言基础，要快速熟练准确地掌握较为困难。事实上数控加工公式曲线的宏程序编制具有一定的规律性，本文以FANUC数控车削为例分析其编程规律及方法。

1 数控车削宏程序中的函数及定义

设D是给定的一个数集，若有两个变量X和Y，当变量X在D中取某个特定值时，变量Y依确定的关系f也有一个确定的值，则称Y是X的函数，f称为D上的一个函数关系，记为，X称为自变量，Y 称为因变量。当X取遍D中各数，对应的Y构成一数集R，D称为定义域或自变数域，R称为值域或因变数域。

由于数控车床使用XZ坐标系，则用Z、X分别代替X、Y，即数控车削加工公式曲线中曲线方程是变量X与Z的关系。其函数为，Z为自变量，X为因变量，若设起点A在Z轴上的坐标值为Za(自变量起点)，终点B在Z轴上的坐标值为Zb(自变量终点)，则D=[Za，Zb]为定义域，X是Z的函数，当Z取遍D中各数，对应的X构成的数集R为值域。当然也可以将进行函数变换得到表达式，即X为自变量，Z为因变量，Z是X的函数。

2 数控编程中公式曲线的数学处理

处理用数学方程描述的平面非圆曲线轮廓图形，常采用相互连接的直线逼近法或圆弧逼近法[1]。一般来说，由于直线法的插补节点均在曲线轮廓上，容易计算，编程也简便一些，所以常用直线法来逼近非圆曲线，其缺点是插补误差较大，但只要处理得当仍可以满足加工需要，关键在于插补段的长度及插补误差控制[2]。曲线的圆弧逼近有曲率圆法、三点圆法和相切圆法等方法。采用圆弧逼近法必须先用直线逼近方法求出各节点再求出各圆半径，计算较繁琐，应用较少[3]。

3 编制公式曲线加工宏程序的基本步骤

数控加工公式曲线的宏程序编制具有一定的规律性，可按如下步骤进行。

3.1 选择自变量

（1）公式曲线中的X坐标和Z坐标任意一个都可以被定义为自变量。

（2）一般选择变化范围大的一个作为自变量。数控车削加工时通常将Z坐标选定为自变量。

（4）变量的定义完全可根据个人习惯设定。例如：为了方便，可将与X坐标相关的变量设为#1、#11、#12等，将与Z坐标相关的变量设为#2、#21、#22等。

3.2 确定自变量的起止点坐标值

自变量的起止点坐标值（即自变量的定义域）是相对于公式曲线自身坐标系的坐标值，如：椭圆自身坐标原点为椭圆中心，抛物线自身坐标原点为其顶点。其中起点坐标为自变量的初始值，终点坐标为自变量的终止值。

3.3 确定因变量相对于自变量的表达式

进行函数变换，确定因变量相对于自变量的表达式。如图1所示椭圆曲线，S点为曲线加工起始点，T点为终止点。对曲线自身而言，起点S的Z坐标为Z10，终点T的Z坐标为Z-10。若选定Z坐标为自变量，则自变量的初始值为10，终止值为-10。

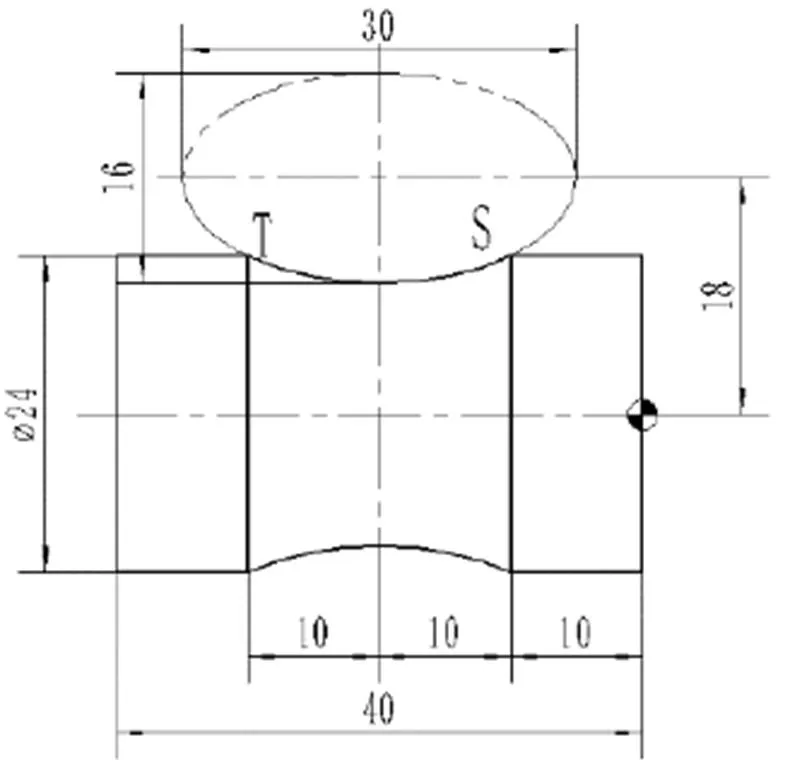
图1 含椭圆曲线的零件图

若用变量#1代表X，#2表示Z，则变量处理结果如表1。

表1 含椭圆曲线零件加工宏程序变量处理表

3.4 公式曲线宏程序编程模板

在编制公式曲线的加工宏程序时，编程的流程如图2和图3所示。

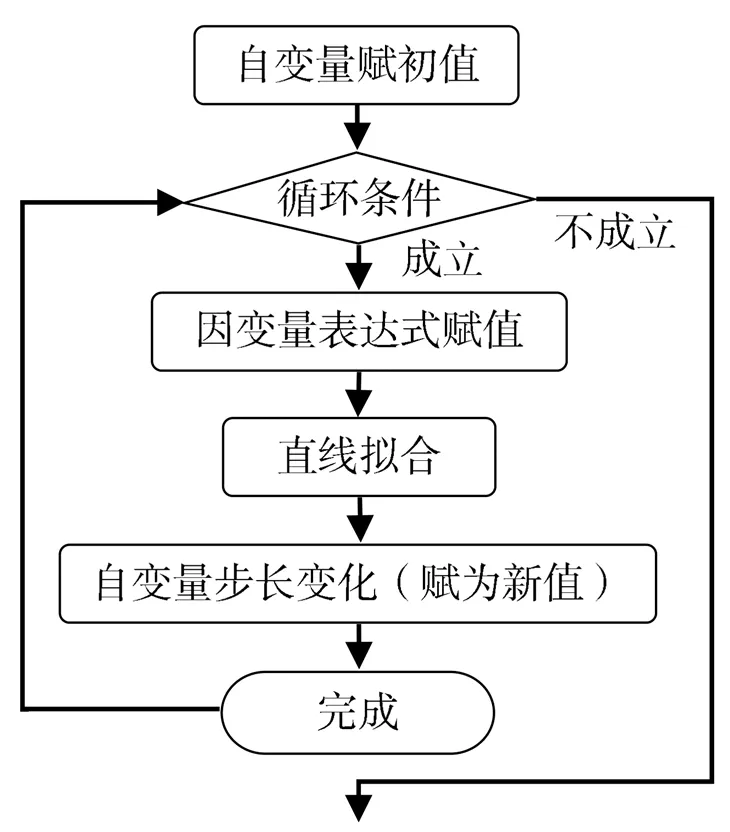
图2 公式曲线加工宏程序流程图(WHILE语句)

图3 公式曲线加工宏程序流程图(IF语句)

根据其流程可按如表2和表3所示进行编程，表中的6个步骤可当成编程模板套用。

例如，数控车削加工如图1所示椭圆曲线，加工刀具刀位点在起始点，要求完成该曲线的数控车削宏程序的编制。

解：设工件坐标原点在工件右端面与轴线的交点上，则椭圆中心(椭圆自身坐标原点)在工件坐标系中的坐标值为(36，-20)，选定Z坐标为自变量，则定义域为[10，-10]，参考公式曲线宏程序编程模板表2编制加工程序如下：

如采用IF语句编程，可参考表3所示的模板，参照上例自行完成。

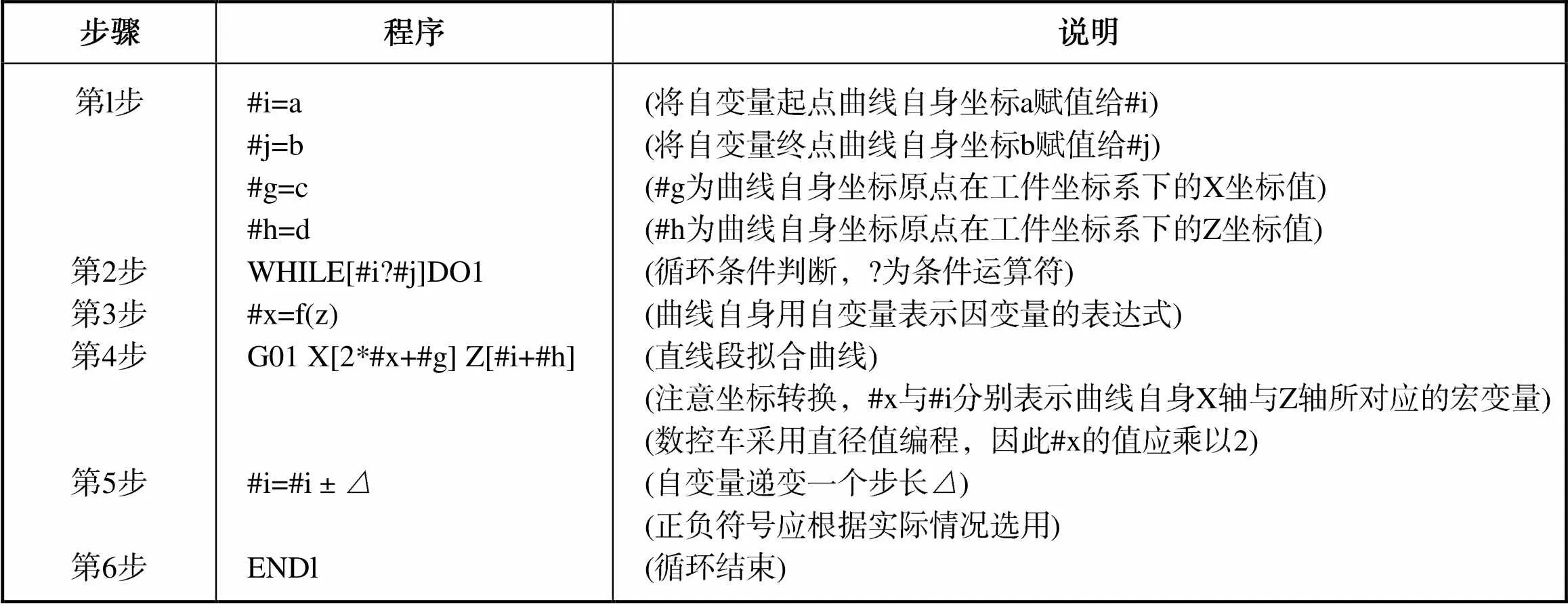
表2 公式曲线宏程序编程模板(WHILE语句)

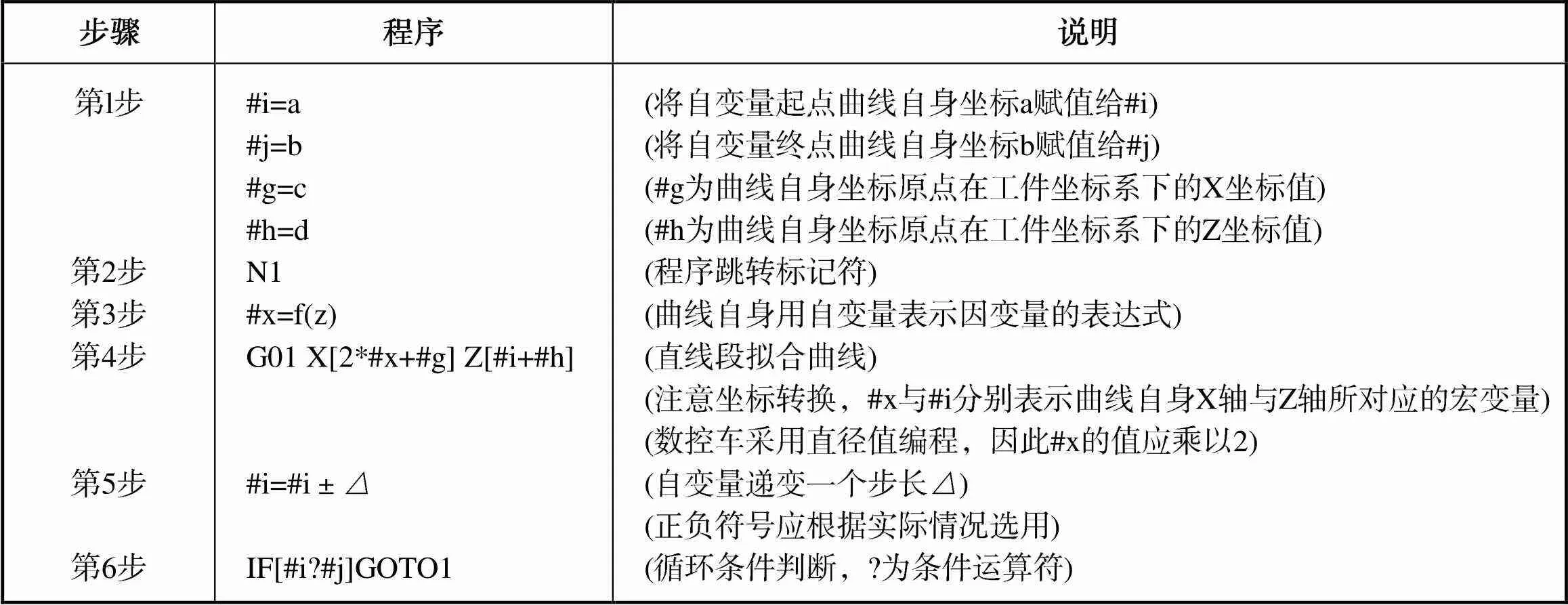
表3 公式曲线宏程序编程模板(IF语句)

4 结语

宏程序编程功能强大，使用方便但相对复杂，然而一旦掌握其规律，编程还是很容易快速实现的。需要强调的是：自变量的选择要使函数计算简单；正确地确定自变量的定义域，即自变量的起止点坐标值；正确地进行函数变换，即确定因变量相对于自变量的表达式。上述问题解决之后，便可参照编程模板进行套用编程，从而使宏程序编程变得不那么让人“望而生畏”。

[1] 刘蔡保. 数控车床编程与操作[M]. 北京: 化学工业出版社, 2019: 39-40.

[2] 刘衍益. 基于宏程序车削旋转椭圆的研究[J]. 机械工程师, 2019 (11): 153-155.

[3] 韦应琴. 宏程序在数控车床椭圆加工中的应用探究[J]. 冶金与材料, 2020 (1): 49-50.

Analysis and Application of the Rule of Macro Programming of NC Turning

Zhang Lin

Starting from the steps of macro program programming of NC turning, this paper analyzes the methods and rules of macro program programming of NC turning, summarizes a more general programming template, provides references for the beginners, and enables the beginners to learn and master the macro programming skills of NC turning more quickly.

NC turning; macro program; programming templates

TG519.1

A

1009－8429(2020)04－0010－04

2020-09-05

张琳（1968 -），男，沙洲职业工学院机电工程系副教授。