经历完整探究过程 关注思维发生发展
——《两位数乘两位数(不进位)笔算》教学实录与评析
执教/王 妍 评析/荆亚琴
【教学内容】
人教版三年级下册第46~48页。
【教学过程】
一、创设情境,整体感知
呈现主题图:每套书有14本,王老师买了12 套,一共买了多少本?
师:要求一共有多少本书?可以怎样思考?
生:可以根据数量关系,每套的本数×套数=购买的总本数,列出算式是14×12。(相机板书)
二、借助点子图,理解算理
1.初步估算,确定范围。
师:14×12,结果大约是多少?
生:把14 看成10,结果是120。
生:把12 看成10,结果是140。
师:通过估算,14×12 的结果大约是一百多。
2.借助点子图,探究方法。
师:这是点子图,一个点表示一本书。借助点子图,把你的想法记录下来。
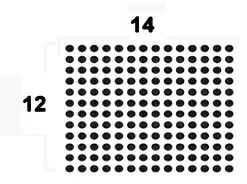
出示活动要求:

呈现三位同学的想法:
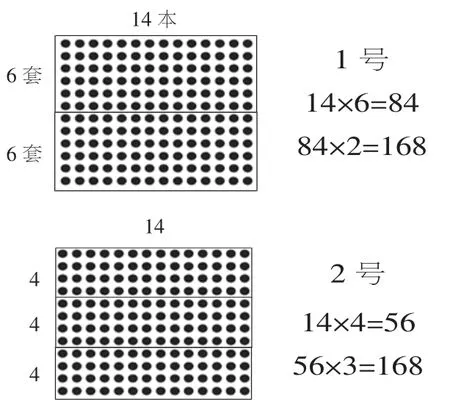
师:看明白他们的想法了吗?
生:1 号先算14×6=84,求出6 套的本数,再算84×2=168,求出12 套的本数。
生:2 号先算14×4=56,先求4 套的本数,再算56×3=168,求出12 套的本数。
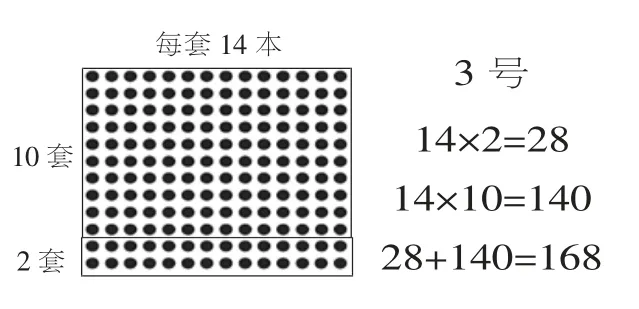
师:大家都想到了把12 拆分成两个一位数相乘,再分别计算。3 号同学的想法,看明白了吗?
生:他先算14×2=28,求出2套的本数;再算14×10=140,求出10 套的本数;最后把结果相加,求出12 套的总本数。
师:拆分的方法各不相同,有什么相同的地方?
生:他们都是通过拆分,变成了我们学过的知识来进行计算。
生:前面两位同学是两位数乘一位数计算,3 号同学则是变成两位数乘整十数、两位数乘一位数计算。
师:把14×12 拆分成两个部分来计算,数学上称为转化,这是一种很重要的数学方法。
3.变化情境,定向理解。
师:如果王老师买13 套书,每套11 本,你还会计算吗?把你的想法记录在《学习单》上。
生:把13 套分成10 套和3套,分别计算出本数再相加。
师:看来,拆分时,我们还要考虑到数据特点。把13 拆分成10 和3,再分别计算,这种拆分方法仍然适用,而第一种拆分方法,就有局限性了。
三、教学笔算,理解算法
1.对比感悟,丰富理解。
师:14×12,还可以笔算。今天,我们就来学习两位数乘两位数(不进位)笔算。(板书课题)
师:笔算,就是用竖式算,列竖式时首先要做到相同数位对齐。(板书竖式)
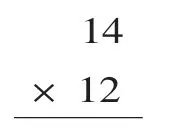
师:你能接着往下算吗?
呈现学生资源:
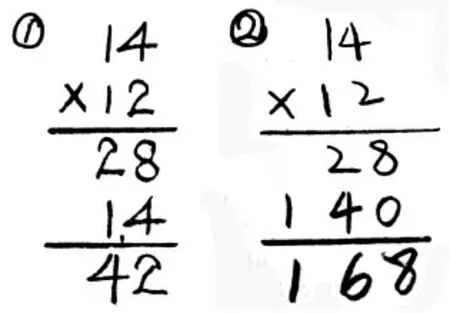
师:都正确吗?
生:①号不对。估算是100多,可笔算才42,所以是错的。
生:①号竖式中,第二个乘数十位上的1×14,结果是14 个十,现在是14 个一,所以不对。
生:②号是对的。先用2 乘14,得到28;再用10 乘14,得到140;最后把28 和140 加起来,得到168。
师:对,列竖式分步计算出每一层积后,积要做到正确对位。
2.示范竖式,明确算法。
师:(借助板演)笔算时,我们先用第二个乘数个位上的2 乘14,算出2 套书的本数是28 本,再用第二个乘数十位上的1 乘14,算出10 套书的本数是140本,4 要对着十位,1 要对着百位,个位上的0 可不写,更简洁。最后计算出168 是12 套书的本数。你能像这样试着说一说笔算过程吗?
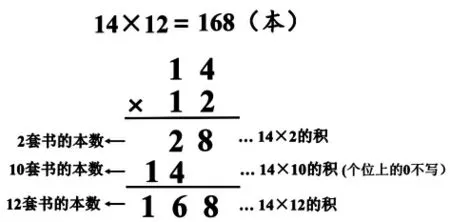
3.比较沟通,联系算理与算法。
师:比较这两种计算方法,你有什么发现?
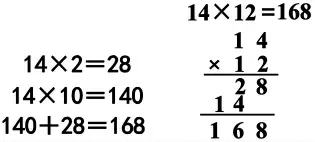
(学生提到竖式的计算过程和点子图表示的意思一样即可)
小结:计算时,两种方法都是先算2 套的本数是28,接着再算出10 套的本数是140,最后把它们相加是168。第一种方法,就是我们进行笔算时的思考过程。
四、巩固练习,内化提升
1.你会计算吗?
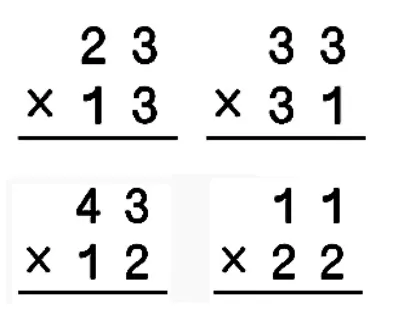
(教师巡视,学生独立计算)
重点交流33×31:
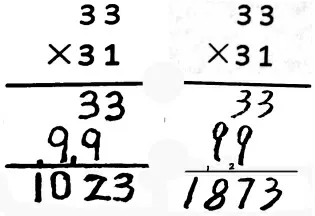
师:同样的计算,结果却不相同,为什么呢?
生:第二位同学肯定不对。33看成40,31 看成40,结果也只有1600,不可能是1873。
生:第二位同学的笔算,最后一步应该用33 加上990,而不是用进位的2 去乘9。
师:有的同学用估,有的同学观察计算过程,都发现了第二位同学计算错误,在分步计算后,最后一步是要把两层积加起来。
2.你会找联系吗?
师:下图一共有多少个鸡蛋?计算后你有什么发现?
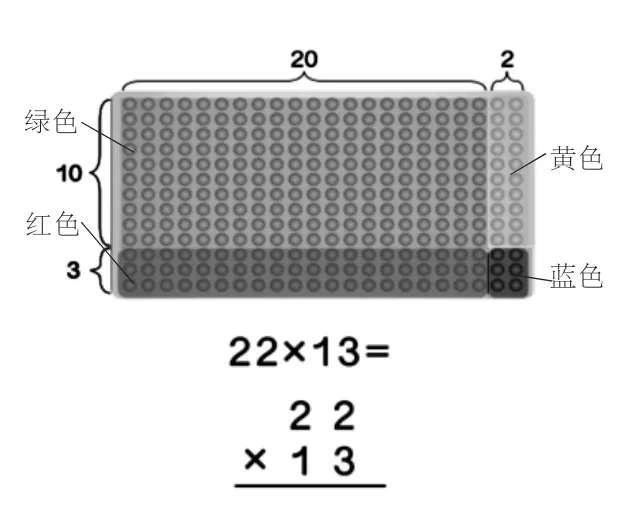
(学生自主计算,并用圈、画等方式表达自己的发现)
师:笔算中,第二个乘数个位上的3 分别乘第一个乘数个位、十位上的2,你能在图中找到表示的那一部分吗?
生:第二个乘数个位上的3,乘第一个乘数个位上的2,图中表示的是蓝色部分,表示3 个2;第二个乘数个位上的3 乘第一个乘数十位上的2,图中表示的是红色部分,表示3 个20。
师:看来,笔算中,虽然两次用到了“二三得六”,但表示的意思却不一样。
(指名说说图中绿色部分和黄色部分表示的意义)
3.你能改错吗?
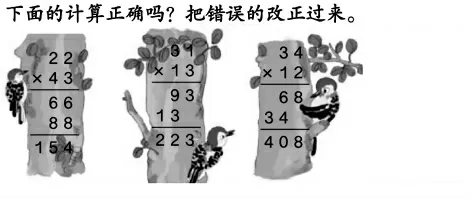
引导学生再次聚焦于第二层积的位置确定。
师:通过刚才的练习,想一想,两位数乘两位数笔算该怎样算?要注意些什么?
4.你会解决吗?
(1)一本书有300 页,如果每天读40 页,7 天能读完吗?如果每天读22 页,两周能读完吗?
(学生独立完成,教师巡视,指名回答)
(2)果园里有11 棵苹果树,平均每棵苹果树可以摘25 千克苹果。如果每5 千克苹果装一箱,一共需要多少个箱子?

(学生独立完成,集体交流)
生:第一位同学,先算出11棵苹果树摘的总千克数,再计算需要的箱子个数。
生:第二位同学,先算出1 棵苹果树的苹果需要5 个箱子,再计算需要的箱子总数。
师:这两种方法都可以计算出箱子的总个数。你更喜欢哪种?
生:我更喜欢第二种方法。计算更方便,只要口算就可以算出箱子的总数了。
师:在解决问题时,我们可以根据问题及数据特点选择合适的方法灵活计算。
五、课堂小结(略)
【评析】
计算教学在小学数学教学内容中占相当大的比例,不仅要处理好“理解算理”“掌握算法”,更需要在解决问题的过程中,注重培养学生判断与选择的意识和灵活敏捷的思维品质。
一、数形结合,理解算理
教材知识的呈现方式内隐着数学知识的认识背景、学生的认知方式、内化途径等。因此,透过教材看教学,我们要思考:“学生学什么?”“学生学习的思维路径是什么?”……正如《数学课程标准(2011年版)》提出的:课程内容的选择要贴近学生的实际,有利于学生体验与理解、思考与探索。
“两位数乘两位数(不进位)笔算”处于整数乘法笔算的断层处,它的难点在于“两层积的对位”和“两层积相加”。而这一内容的学习,将为后续如三位数乘两位数、小数乘法等笔算提供算理、算法支撑。对于这类处于知识转折点的教学内容,教师在教学时,就需要借助学生已有的生活经验(如例题中的数量关系)或是图文表征(如点子图),为学生理解笔算的算理提供思维的支持。正因此,王老师在教学中,充分发挥点子图的直观作用,学生借助点子图圈一圈尝试求解,这里的圈,如果脱去数量关系这层外衣,不仅可以横着圈,更可以竖着圈。这样,学生的思维空间随之打开,他们的每一种方法都真实地记录了自己的思维过程,而这,也为学生从直观视角理解拆、算的道理提供了认知保障。学生在圈一圈的过程中,很自然地就把直观操作与口算的过程、竖式的理解有机地联系起来,有助于学生实现算理与算法、直观与抽象、点子图与竖式等的沟通,让学生在自我建构中理解算理、掌握算法。
二、有效沟通,掌握算法
理解算理,学生才能进一步掌握算法,而算法的构造不是一蹴而就的。学生在借助点子图解决问题的过程中,不同学生的思维状态必定不同,这就需要教师有敏锐的学习资源捕捉意识。王老师已经有了资源的“类”意识,她通过并列呈现两位数乘一位数和两位数分别乘整十数、一位数的资源,组织学生比较多种算法的相同点,体会应用转化求解新问题的思路。在此基础上,王老师进一步提出“如果买13 套书,每套书11 本,你还会计算吗?”让学生在多元算法中进一步优化,认识到把两位数拆分成整十数和一位数,更具有普适性。在初步理解14×12 的笔算方法后,王老师及时把竖式与学生的生活经验、点子图进行横向沟通,让学生知其然,更知其所以然。练习阶段,王老师特别使用了数鸡蛋个数的实物模型。伴随着学生对点子图、两位数乘法笔算的进一步抽象,学生对乘法笔算的认识也逐步从特殊(口算)走向一般(笔算),由具体(点子图)走向抽象(笔算),学生头脑中笔算竖式的表象也越来越深刻。
三、问题解决,发展思维
本节课练习部分,王老师有意识地设计了指向于培养学生灵活、敏捷等思维品质的习题。根据问题情境及数据特点,灵活选择算法。如解决苹果包装的问题,受定向思维影响,学生往往会选择先计算出11 棵苹果树可以摘的总千克数,再计算需要的箱子个数。当多数学生选择第一种方法计算出正确答案后,王老师没有戛然而止,而是有意识地通过学生两种学习资源的对比,让学生进一步明白,在计算时我们可以根据数据特点,判断和选择恰当的方法进行灵活计算,从而帮助学生逐步建立数学敏感。
计算教学承载着丰富的育人价值,学生在学习计算的过程中,收获的不仅仅是计算方法,更重要的是在探索过程中领悟到的数学思想和方法,并且在这一过程中不断发展的判断与选择的自觉意识和灵活敏捷的思维品质。因此,教师在教学中,不仅要关注学生计算技能的习得,更要关注学生运算能力的提升,关注学生思维品质的发展。

