我国智能产业优惠政策对智能效率的影响效应实证研究——基于企业生产系统的微观视角

吴淑娟

(五邑大学经济管理学院，广东 江门 529020)

我国智能产业备受政策眷顾但非效率现象频发。这引发了智能政策效应如何的疑问。有关优惠政策效应的争议由来已久。政府可依据产业发展过程中成本与外部性变化，制定最优补贴强度，逐步降低政策扶持力度直至行业具备竞争力。最终有利于提高行业生产率。但信息不对称和受惠对象的选择成本等问题导致资源错配，扭曲企业行为，造成全要素生产率(TFP)损失。加上市场不完善或摩擦带来资源错配，影响企业的技术选择和市场决策，进一步恶化生产率损失[1]。因而出现了正效应论、税收优惠(简称“减税”)更佳论、政府补贴(简称“补贴”)中性论、两者无用论观点。

可见，扶持政策对效率的影响研究颇受重视。优惠政策对效率的效应因研究对象、考察期间、所选指标和样本等不同而迥异。现有研究的不足主要是大多研究忽略了智能知识产出，未能区分补贴和减税对智能知识产出的影响以及两种政策对两种产出的间接效应。扶持政策的交叉影响很可能扭转扶持政策的效应。因而本文从智能企业运作系统的微观视角出发，实证减税和补贴对智能效率的影响，最后根据实证结果提出对策启示，为政策调整提供参考。

1 构建模型

按企业运营过程的特点，把智能企业生产的大系统分成技术研发(简称“系统1”)和生产销售(简称“系统2”)两个子系统。我国智能补贴主要针对技术研发，减税主要针对增值税和所得税，两者对产出的影响有先后之别[2]。假设系统1的投入要素有研发资金投入和高层次人才，产出有非物化的智能技术专利等智能知识产出。系统2的投入要素有系统1的智能知识产出、低级劳动力和资金投入，产出是产品销售收入。

令智能企业自有研发资金投入为KRD，补贴为S，研发人员为HE，系统1的智能知识产出为IP。基于根据C-D函数，加入补贴变量S，对函数公式取对数，得补贴对系统1效率的短期影响模型为：

TFPit1=a10+a11lnHEit+a12lnKRDit+a13lnSit+a14lnIPit+εr1

(1)

其中a10为常数，a11、a12、a13、a14分别为系数，i代表企业，t代表年度。补贴对自有研发资金的挤出效应、信号作用和激励作用的综合影响在中期得以凸显。减税(PT)的间接作用也得到了体现。因减税的间接效应具有时滞性，加入减税滞后一期(PTt-1)，得补贴和减税对系统1效率的中长期影响函数：

TFPit2=a20+a21lnHEit+a22lnKRDit+a23lnSit+a24lnPTirt-1+a25lnIPit+εr2

(2)

令系统2劳动力投入为LE，营业成本为GK，产出为Y。构建系统2的短期生产函数，再对该函数取对数，得减税对系统2的短期影响模型：

TFPit3=a30+a31lnLEit+a32lnGKit+a33lnPTit+a34lnIPit+a35lnYit+εr3

(3)

又因长期效应的时滞性，减税和补贴对系统2效率的中长期影响模型为：

TFPit4=a40+a41lnLEit+a42lnGKit+a43lnSipnst-1+a44lnPTit+a44lnIPit+a45lnYit+εr4

(4)

其中S=Sr+Spns。Sr为科研子系统的补贴，Spns为间接转移至系统2的补贴。PT=PTr+PTpns。PTr为间接转移至科研子系统的减税，PTpns为系统2的减税。

综合模型(1)和(3)的分析，补贴和减税对大系统的短期影响模型为：

TFPit5=a50+a51lnLEit+a52lnBCit+a53lnHEit+a54lnKRDit+a55lnSit+a56lnPTit+a57lnYit+e5

(5)

补贴和减税分别对子系统均有直接或间接效应。减税对系统1的影响用PT与系统1的KRD的交叉项滞后一期表示。补贴对系统2的影响，用S与系统2的GK的交叉项滞后一期表示。优惠政策对大系统的中长期效应模型为：

TFPit6=a60+a61lnLEit+a62lnGKit+a63lnHEit+a64lnKRDit+a65lnSit+a66lnPTit+a67lnYit+a68lnSit-1×GKit-1+a69lnPTit-1×KRDit-1+e6

(6)

2 变量、数据和实证过程

2.1 变量指标的选择

智能效率采用智能TFP、技术效率TE、纯技术效率PE和规模效率SE代表。从证交所智能板块企业库中，剔除2011年及其后上市的企业样本，随机选择82家智能上市企业数据。用DEAP 12.0软件，运用DEA-Malmquist指数法，采用2011—2018年的上市企业数据，分别以高层次人才数量、智能研发资金为系统1的投入变量，以智能知识产出为系统1的产出变量，以低层次劳动力投入、经营成本为系统2的投入变量，以营业收入为系统2的产出变量，测算子系统和大系统的效率值。智能技术研发投入采用年度科技资金投入金额来代表。高层次人才投入采用本科及以上人才的数量来代表。低层次劳动力投入量采用生产工人数量指标代表。智能知识产出采用剔除了土地使用权以外的无形资产金额代表。经营资金投入采用经营总成本金额代表。总产出采用主营业务收益额来代表。补贴采用补贴金额来代表。减税采用应缴所得税率和实缴税率的差代表。

2.2 样本数据的选择和处理

2012—2018年间的数据，共574条数据样本。数据统计性描述见表1。对环境变量数据标准化处理，采用Stata 15.0软件进行运算。

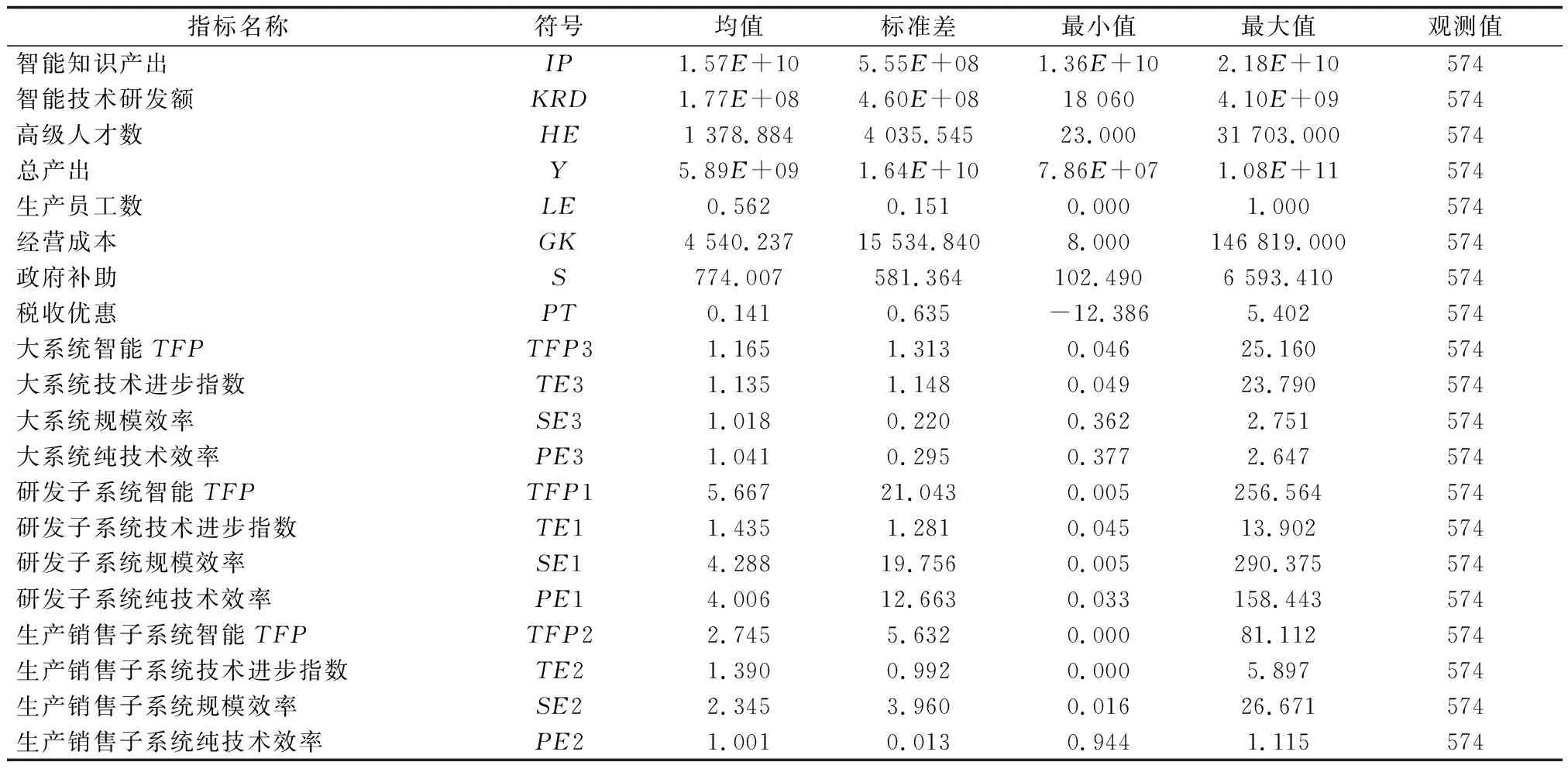
表1 数据统计性描述

2.3 实证过程

使用包括LLC、IPS、ADF-Fisher等方法进行平稳性检验，综合P值结果，变量均不支持含有单位根的原假设，符合平稳性的计量要求。采用Panel-rho-Statistic、PP-Statistic、ADF-Statistic和分组PP-Statistic、ADF-Statistic检验。结合F检验、LR检验和Hausman检验结果，变量基本上通过协整检验。

对智能企业的子系统和大系统数据分别进行固定效应面板线性回归和门槛回归。

3 实证结果及结果分析

表2和表3分别是线性回归和门槛回归结果。其他结果因篇幅有限，未能列出。

在系统1，补贴与TFP线性正相关。减税对系统1TFP有微弱正效应，其间接效应助推了补贴对系统1的TFP正效应。亦即补贴对自有研发资金的短期挤出效应弱于其信号作用和对研发活动的激励作用，因而对系统1效率有正作用；减税也影响自有研发资金投入，促进研发活动；智能政策有效提升系统1的效率。此发现与文献[3]的发现相符。该文认为政府支持对高技术产业技术创新效率有正效应。

在系统2，减税与TFP有非线性单门槛回归关系，亦即当减税大于11.1%之时，减税对智能TFP的影响从轻微负相关变成强烈且显著负相关。但补贴，使得减税对TFP的负效应稍有减缓。系统2的资金投入因减税和补贴的影响，对智能TFP的影响系数逐渐增强。补贴和减税对系统2的TFP有负效应，后者的负效应强烈。这进一步印证当前智能产业政策具有针对研发活动的专向性。

在大系统中，优惠政策对智能TFP基本上呈非线性关系。减税对大系统智能TFP有倒U型单门槛效应。但该门槛值畸高。补贴对减税的影响极其微弱。表明现实中，减税多为正效应。

补贴对大系统的智能TFP也有倒U型单门槛效应。根据门槛值，得拐点为补贴0.119万元。现实中，大多数智能企业享受的补贴能超越门槛值。减税的间接效应把补贴对大系统智能TFP的关系变成线性关系。在中长期呈现出轻微的负效应。最终，两种举措均对大系统智能TFP有负效应，其中补贴的负效应更为强烈且显著。两者与智能TFP的短期倒U型关系，很有可能是因为两种政策对企业自有研发资金的挤出效应滞后而致，也符合孟庆玺等关于产业政策能增加受惠企业的研发强度，且影响程度呈出“先升后降”的动态变化趋势的观点[4]。文献[5]的发现与本文不一致，可能是因为前者采用大系统的创新效率，与本文的指标有异。这印证了本文最初的观点，即有两种优惠政策对智能效率确实有直接和间接效应。政府优惠对不同子系统的效率的影响差异甚大，体现出智能优惠政策的智能效率效应的复杂性。仅以大系统效率为指标研究，往往难以作出全面的判断。

效应来源分析时因篇幅有限，未列出具体结果。

补贴对系统1的效率的正效应主要来自规模效率的贡献，其次是纯技术效率，而技术效率的贡献较弱。减税对系统1的间接效应加强了补贴对系统1智能TFP的正效应。减税对系统1智能TFP亦有微弱的正效应。

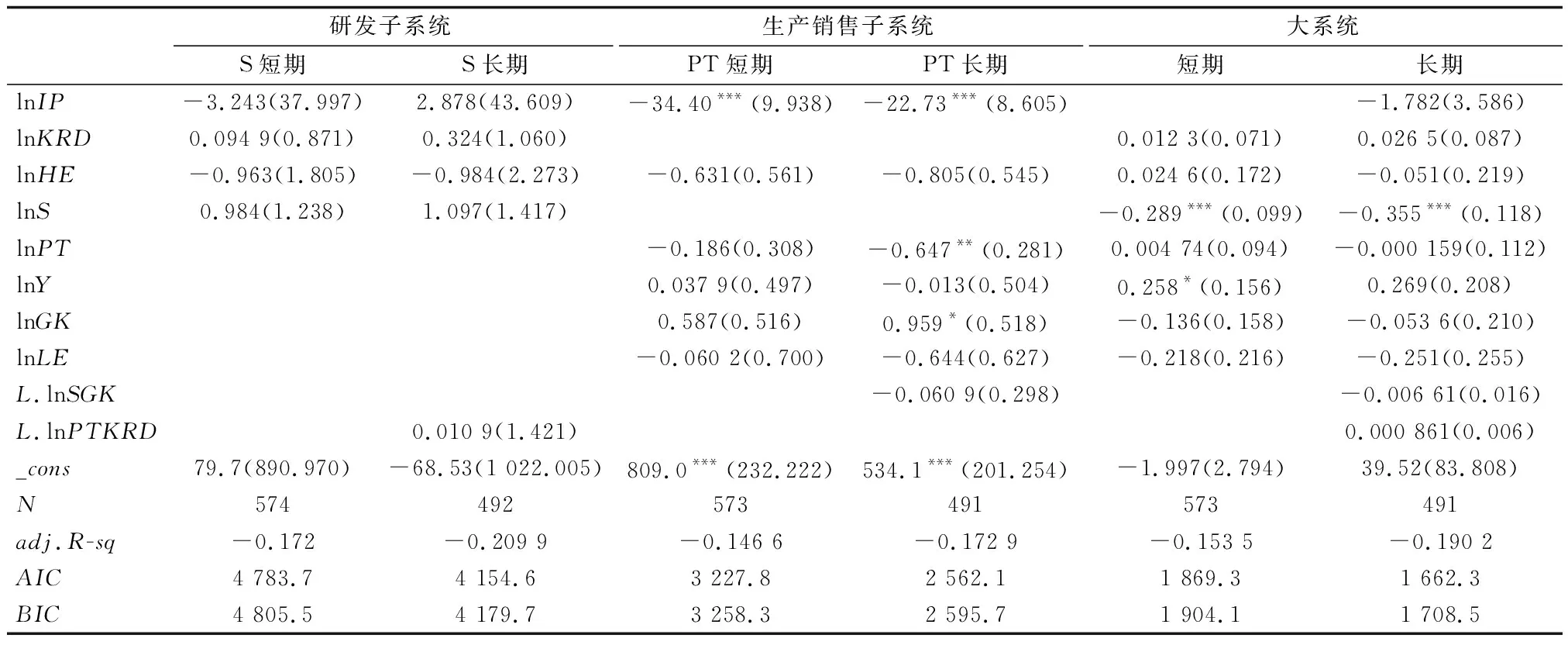
表2 TFP为因变量的固定效应回归结果

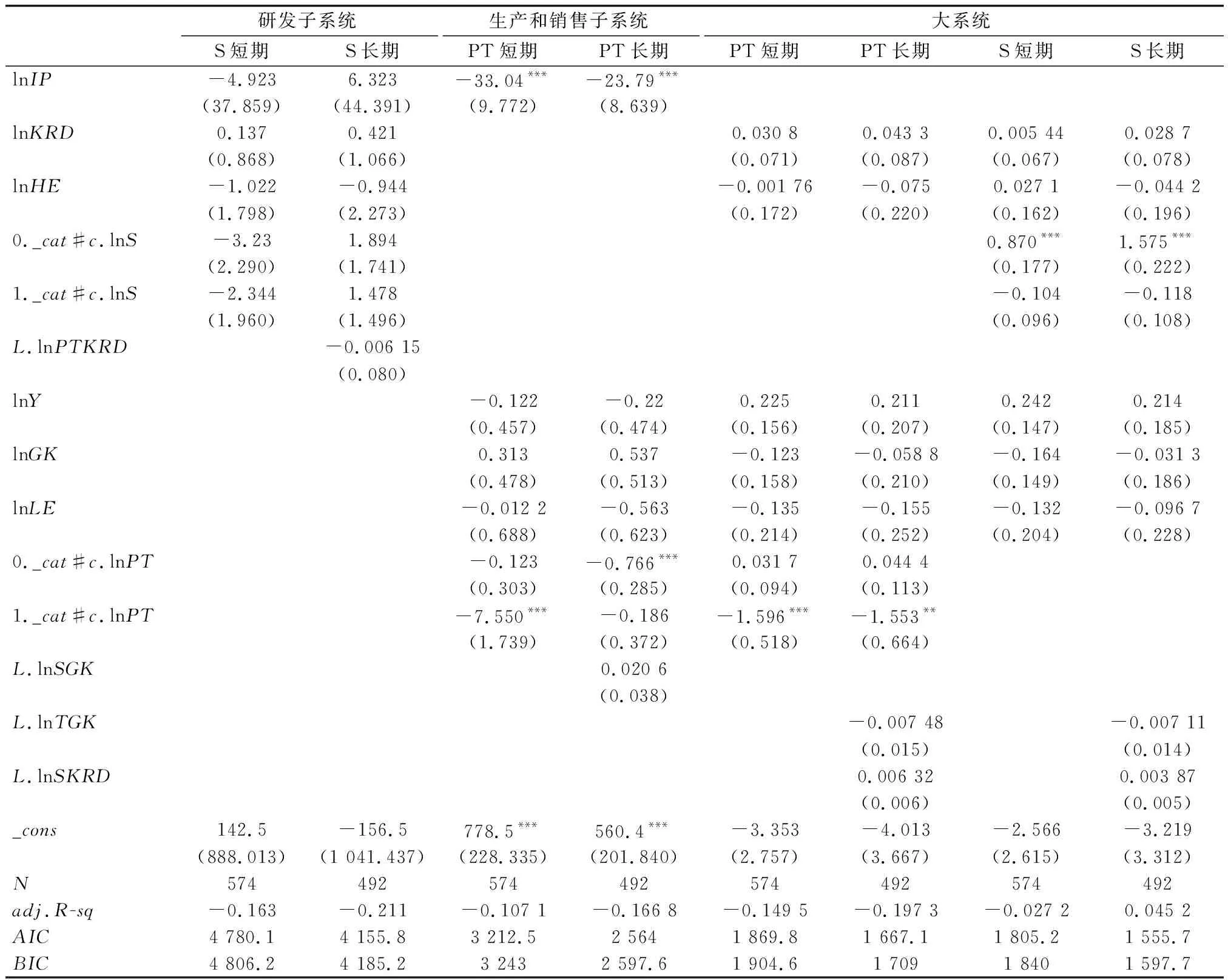
表3 门槛回归结果TFP为因变量

减税对系统2的效率的负效应主要来源于规模效率的负效应。减税对技术效率和纯技术效率的效应均较微弱。补贴对系统2的间接效应基本上恶化了减税对系统2的效率的效应。补贴与生产销售资金投入共同对系统2的智能效率形成负效应。

大系统方面，补贴对大系统智能TFP的强烈负效应；减税对大系统智能TFP的微弱的负效应。产业政策对企业研发强度的激励作用主要是通过补贴、减税等“资源效应”实现。“资源效应”容易导致资源配置的非效率、规模不经济，从而带来了纯技术效率、技术效率和规模效率的负效应。可见，规模效率是当前智能优惠政策对智能效率的效应的主要影响因素。吴淑娟等的研究也有类似的发现[6]。在系统1的正效应主要由规模效率带动，系统2的负效应主要由规模效率带动，也表明当前智能技术创新尚未成为效率增长的主要驱动力。

上游环节优惠政策与智能TFP的关系。上游环节优惠政策与智能TFP多为线性关系。补贴与系统1的TFP有正的线性关系。减税对智能TFP的正效应主要来源于纯技术效率和技术效率的正效应，规模效应的负效应非常强烈。

减税与系统2智能TFP有正相关线性关系。在补贴的影响下，减税与该系统的智能TFP存在单门槛回归关系，呈U型关系。

大系统方面，补贴和减税对大系统的智能TFP均有负效应。补贴的负效应强于减税。在两者的影响下，系数均稍有减弱。

中游环节优惠政策对智能效率的效应。中游环节优惠政策对智能效率的效应表现出较强的规律性。在系统1，补贴具有强的正效应，加上减税的间接作用，补贴的效应进一步增强且显著。减税对系统2的影响主要是非线性关系，呈倒U型关系。补贴的影响使得减税对智能效率有微弱的负效应。减税的负效应主要来自纯技术效率的负效应。大系统方面，在两种举措的交叉作用下，补贴和减税对智能TFP具有负效应。

下游环节优惠政策与智能效率的关系。下游环节的优惠政策与智能TFP以线性关系为主。在系统1，补贴与智能TFP正相关，而减税在系统1有负效应。在系统2，减税与智能TFP有显著的负效应，在补贴的负面影响下，减税的负效应加强。在大系统，政策扶持与智能效率以线性关系为主。其中补贴有显著的负效应。减税对智能TFP则有正效应。

4 结论与对策启示

实证结果表明，补贴和减税分别在两个子系统有不同的效应。总体上，补贴在全产业链和各环节的企业系统1均有正效应，但在大系统却表现出倒U型的非线性关系或线性负效应。全产业的减税在系统2的智能效率负效应，但在各环节的效应差异甚大；减税在大系统的倒U型效应也有异于各环节的效应。这体现出优惠政策对智能效率的影响的复杂性，仅从大系统的视角研究优惠政策的智能效率效应难免有片面性。

优惠政策之间交叉影响。补贴和减税相互之间存在影响。这种间接效应或缓释或加强另一种优惠政策的效应。补贴对全产业减税的间接效应则相对微弱，基本上未能从根本上扭转减税对智能效率的效应方向。

为此，应在以下方面多加注意：一是实行普惠性的补贴政策，降低补贴门槛。建议实行普惠性的补贴政策，降低享受补贴政策的门槛，提高享受补贴政策的便捷度。二是减税可以作为长期的优惠政策。建议以减税作为长期的优惠政策，特别是加大上游环节企业的减税幅度和受惠范围。三是发挥优惠政策的间接正作用。四是注重扩大产业规模。今后在扩大现有企业规模的同时，加快培育新企业。采取促进技术进步和市场扩大的举措，引导智能企业加强管理，以拓宽产品的开发和销售来促进企业规模扩大，进而促进行业规模扩大。培育有自主知识产权的科技型企业，加快智能高新技术产业的形成和发展。