基于三维悬垂模型和织物面密度的织物匹配
余志才, 钟跃崎,2, GONG R Hugh, 谢昊洋, HUSSAIN Azmat
(1. 东华大学 纺织学院, 上海 201620; 2. 东华大学 纺织面料技术教育部重点实验室, 上海 201620;3. 曼彻斯特大学 材料学院, 英国, 曼彻斯特 M139PL)
织物匹配是指从多种织物样本中锁定与给定织物性能相近的织物,这对于服装设计和面料优化都具有重要的意义。到目前为止,关于织物匹配的研究都是基于织物在平铺状态下的纹理图像[1-2],这些方法不能比较织物的内在力学性能。考虑到织物的悬垂形态是织物内在属性的最直观体现,因此本研究将织物的三维悬垂模型应用到织物的匹配中,探究基于织物悬垂模型实现织物快速匹配的可行性。到目前为止,关于织物悬垂性能的研究大部分集中在优化织物的结构参数、力学性能或后处理工艺来提高织物的悬垂性能和成衣性,而对织物的悬垂性能有针对性的比较分析还较少。随着三维扫描技术的发展,悬垂织物的研究对象也由传统的二维俯视图像扩展为三维的点云或网格模型。然而,关于悬垂织物三维模型的研究都集中在悬垂织物三维模型的获取,很少有学者对悬垂织物的三维点云或网格深入分析,例如:王寿兵等[3]通过识别全景光栅图像中的等高线信息,定位光栅条纹,得到光栅条纹所处空间高度,从而确定了悬垂织物三维模型;Mah等[4]用三维人体扫描仪扫描了悬垂织物的三维形态,统计了悬垂织物的截面轮廓线与支撑圆柱之间距离的分布;施祖平等[5]设计了织物悬垂三维形态测试系统,该系统能够建立试样悬垂形态的贝塞尔曲面数学模型。为简化三维重建的装置,胡堃等[7]提出了利用手机镜头采集图像序列进而实现重建三维悬垂模型的方法。以上文献均具有一个共性,即对获取得到的悬垂织物三维模型没有对比分析,对于织物悬垂模型不能有效地识别和区分。产生这种现象的原因在于三维的模型具有顶点密度和网格密度等属性。要比较分析不同的悬垂织物三维模型,必须将模型的顶点数目和网格拓扑结构统一,使不同的模型之间具有可比性。然而,到目前为止还没有关于悬垂织物三维模型网格统一化的报道。另外一个影响三维悬垂模型比较分析的原因是织物的悬垂变异性,Niwa等[8]测试了145种女性服装面料和138种男性面料,其结果表明在相同的实验条件下,相同的织物可以具有不同的悬垂系数,织物悬垂系数的变异系数与弯曲滞后力矩成正比,并且与织物面密度成反比;文献[9-11]也分别验证了织物悬垂的离散特性;虽然织物的悬垂结果具有离散特性,但是考虑到相同织物在多次悬垂实验中没有发生结构的破坏,由于结构决定性能[12],因此相同织物多次悬垂的结果一定存在共性。经过对比观察,本研究发现相同织物的多组悬垂模型在局部形变方面非常相似。因此可以用悬垂织物三维模型的曲率分布情况来表征织物的悬垂形态。
基于此,本文首先利用自主搭建的悬垂织物扫描装置扫描了悬垂织物的三维网格模型;采用局部线性嵌入算法将悬垂织物三维网格展平(降维),进而实现三维网格模型重采样;并提取悬垂织物三维网格的曲率统计直方图,以悬垂织物三维模型的曲率统计直方图和织物面密度为依据实现悬垂织物的匹配。
1 实验材料和方法
1.1 织物样本的准备
将从市场上采集的51种织物样本洗涤并熨烫处理,以除去织物表面的褶皱。其中51种织物包含10种棉织物、9种麻织物、9种丝织物、5种毛织物和18种化纤织物。将织物样本裁剪成半径为120 mm的圆形样本,标记中心点位置。将织物在恒温恒湿实验室(温度(23±2) ℃,湿度(65±2)%)调湿48 h。
1.2 扫描装置的搭建及相机标定
参照毋戈等[13]的方法利用4个深度相机搭建三维扫描装置,该装置的结构如图1所示。
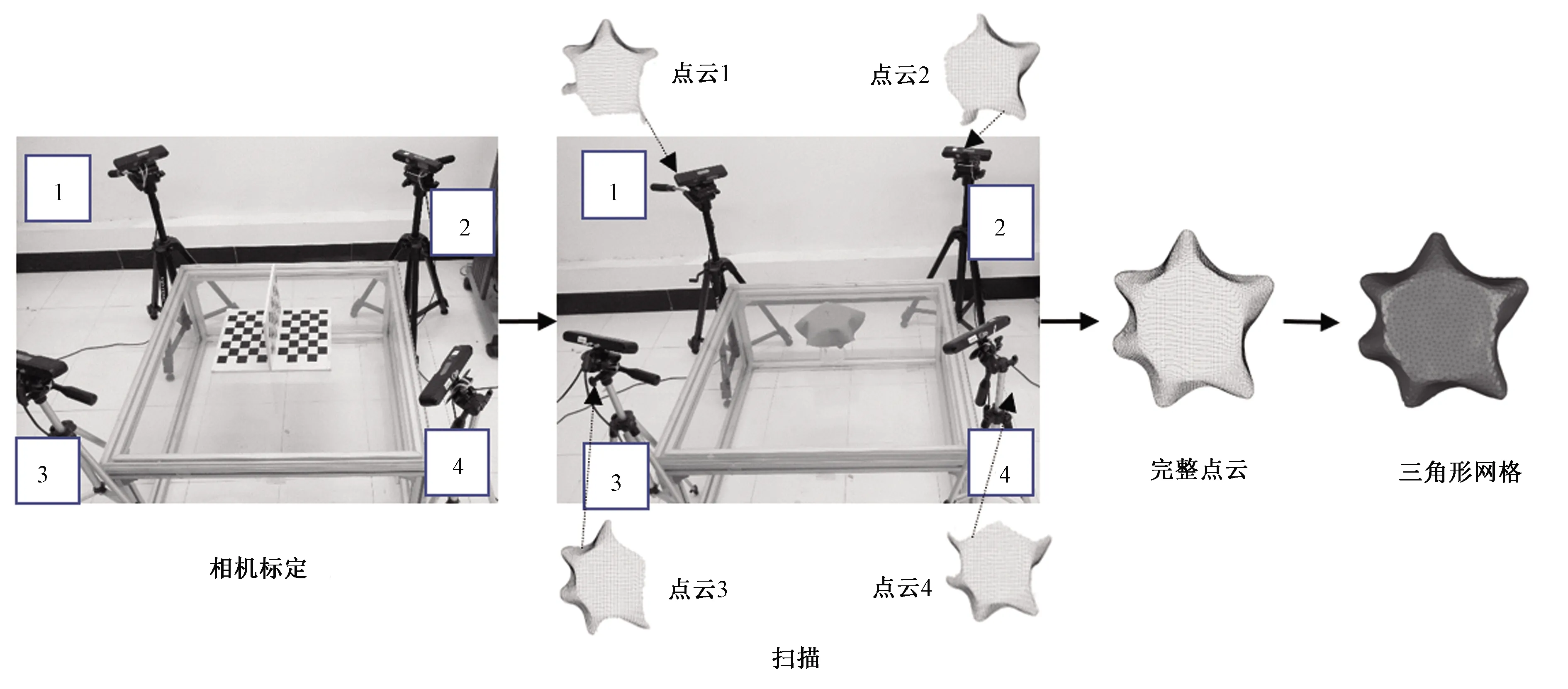
图1 悬垂织物三维模型扫描装置及流程Fig.1 Scanning device of draped fabric and pipeline of capturing drape model
与同一台计算机相连的4个RGB-深度摄像头分布到标定板的四周。为避免4个深度摄像头采集信息的过程中相机投射的红外斑相互干扰[14-15],在实验中控制4个摄像头依次扫描,获取悬垂织物不同方位的场景信息。为将各个方位的场景信息组成完整的场景信息,参照毋戈等[13]提出的基于T形标定板的张正友标定法对相机标定。相机标定完成后将织物样本悬垂到半径为60 mm的支撑圆盘上,二者圆心重合。将标定板换成支撑圆盘和待测织物,扫描获取完整的悬垂织物三维点云,在三维逆向工程软件“Geomagic”中将点云封装为三角形网格。对于实验中使用的51种织物,每种织物扫描3次,共计153个扫描模型。
1.3 以织物悬垂指标为特征实现织物匹配
在对比实验中使用悬垂织物的3个悬垂指标作为特征并结合织物面密度实现织物匹配。这是因为织物的悬垂指标之间都具有非常高的相关性,没有必要将悬垂织物的所有表征指标都串联起来作为织物匹配的依据[16]。其中表征织物悬垂能力方面选择悬垂系数,这是因为悬垂系数作为表征织物悬垂能力的指标得到了广泛的应用。在表征织物悬垂形态方面,Carrera等[17]证明织物的悬垂瓣角数目(N) 和织物的实心度(Rs)能够表征织物的悬垂形态,因此将这3个指标组合成为一个特征向量用于织物悬垂模型的匹配。
基于织物悬垂指标和织物面密度的织物匹配方法如下所示。计算给定织物对应的悬垂指标与待匹配织物对应的悬垂指标之间的欧式距离,然后对距离排序,得到待匹配织物与给定织物的悬垂模型相似度排序结果O1。排序越靠前,待匹配织物与给定织物的匹配织物的三维悬垂模型越相似。然后计算待匹配织物与给定织物的面密度之间的欧式距离,得到待匹配织物与给定织物的面密度相似度排序结果O2。然后根据下式计算每个待匹配织物与给定织物的相似度的综合排序O。
O=0.5×O1+0.5×O2
1.4 基于曲率统计直方图的织物匹配
为使得不同模型具有可比性,提出了基于局部线性嵌入的悬垂织物网格重采样方法,主要分为4步。
1)计算悬垂织物网格模型的三维边界线总长度L3D,然后将三维边界线上的离散点投影到周长为L3D的二维平面圆上,如图2所示。
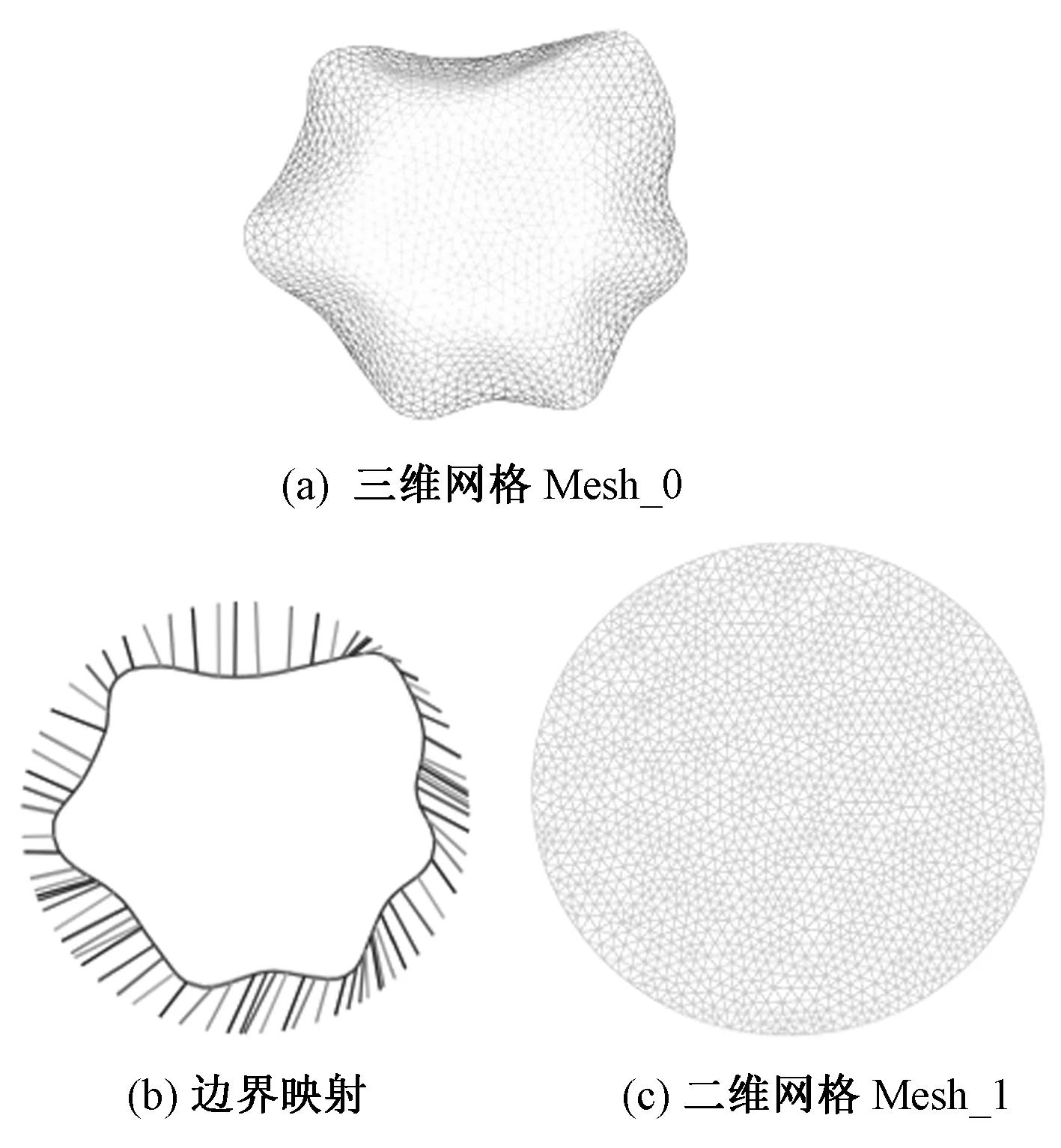
图2 悬垂织物三角形网格Fig.2 Triangle mesh of draped fabric. (a) 3-D triangular mesh (Mesh_0); (b) Mapping of 3-D boundary; (c)2-D triangular mesh (Mesh_1)
2)以投影后的二维平面圆上的点为约束点,对悬垂织物三维网格局部线性嵌入。该方法的优点在于降维后数据仍然能保持原有的拓扑结构,即降维前悬垂织物的网格模型(Mesh_0)与降维后悬垂织物的网格模型(Mesh_1)具有相同的三角形拓扑结构。
3)生成一系列同心圆,然后在同心圆上均匀采样,最终得到均匀的离散点,如图3(a)所示。其中同心圆的最大半径为120 mm;重叠图3(a)和图2(c), 即将图3(a)中点映射到Mesh_1中,结果见图3(b)。
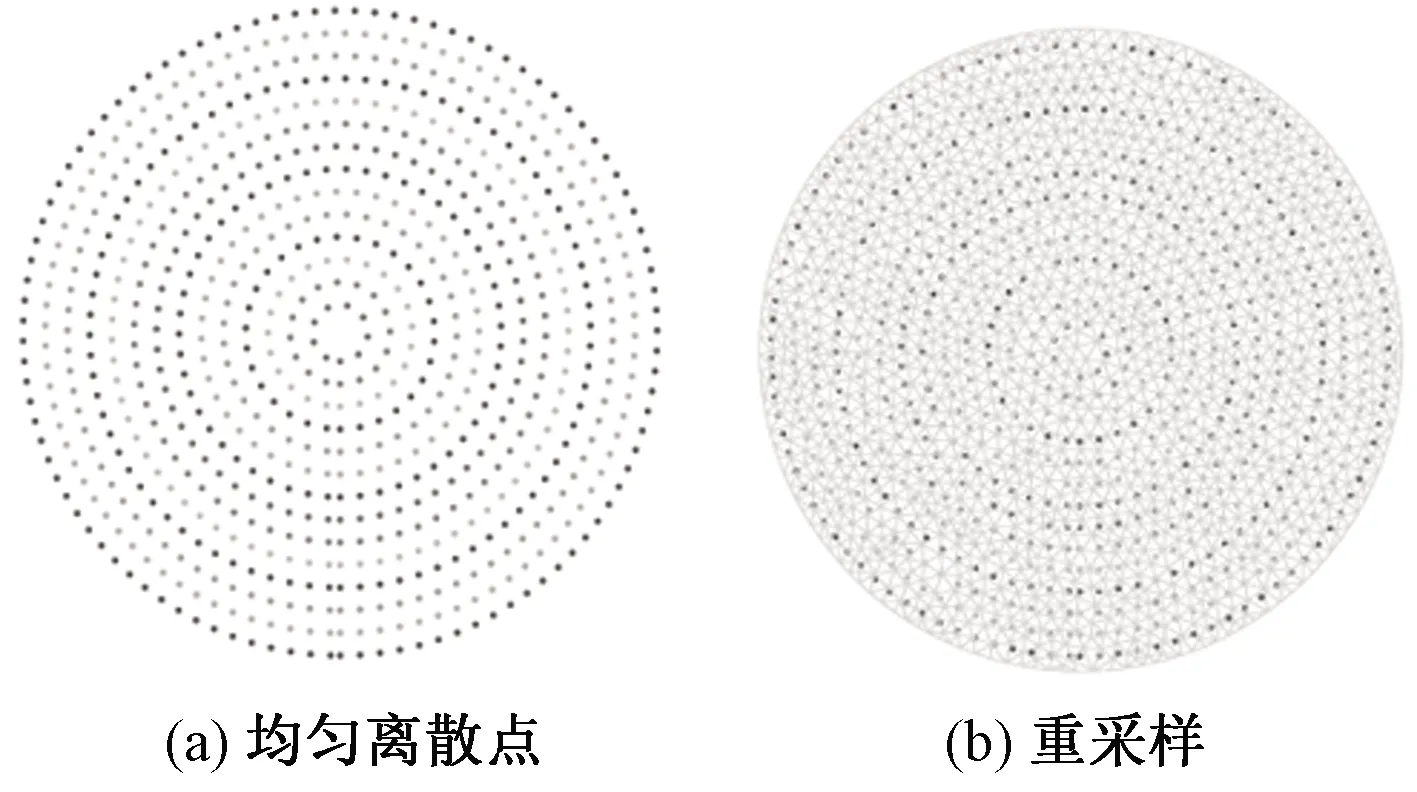
图3 均匀分布的离散点与重采样Fig.3 Points with uniformly distribution(a) and resampling triangular mesh (b)
Mesh_0中三角形与Mesh_1中对应三角形的关系如图4所示。
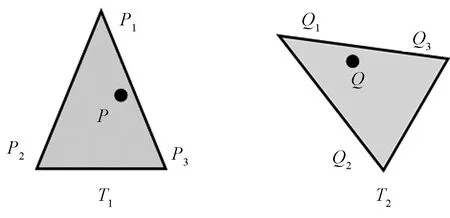
图4 空间三角形与其对应投影三角形示意图Fig.4 Schematic diagram of 3-D triangle and corresponding mapped triangle
T1是Mesh_1中的三角形,T2是Mesh_0中的三角形,且T1和T2具有相同的三角形索引。若离散点t是图3(a)中一点,其在图3(b)中的映射为P。则点P与顶点P1、P2、P3的关系如式1所示,
P=mP1+nP2+(1-m-n)P3
(1)
式中,m和n均是0~1之间的系数。Sez等[18]证明织物在悬垂过程中由拉伸引起的形变非常小,几乎可以忽略。因此三维模型降维后的模型类似于织物在未悬垂时的状态,而且降维前后模型的三角形拓扑结构保持不变,综合以上因素,离散点t在Mesh_0中的映射点Q可以根据点P的权重系数求出,即
Q=mQ1+nQ2+(1-m-n)Q3
(2)
4)计算重采样悬垂模型中每个顶点处的最大曲率值,并统计每个悬垂模型的曲率直方图。在本实验中每个重采样悬垂模型包含4 819个顶点和9 479 个三角形,参与曲率计算的邻域数为15,该条件下悬垂织物网格模型的曲率分布较为均匀,计算量相对较小。经验证本文最终确定了分组数为40的曲率统计直方图。
以悬垂模型曲率统计直方图结合织物面密度实现织物匹配的方法与1.3节所示方法相同,在此不做赘述。
1.5 基于力学特征的织物匹配
在织物匹配的评价方面,参考武松梅等[19]的模糊相似优先比矩阵法,本文提出用构造模糊相似矩阵的方法计算织物与待织物的匹配织物之间的距离,将利用该方法计算得到的结果作为织物匹配的评价依据。王新洲等[20]对现有的13种模糊相似矩阵构造方法全面比较,证明了绝对值倒数法最适合构造模糊相似矩阵,因此本文采用绝对值倒数法来构造模糊相似矩阵,
(3)
(4)
式中:rij为样本i与样本j的相似程度;rij的值越大表示样本i与样本j之间的相似度越大;c为常数;m为特征的长度;xik和xjk分别为样本i、j的特征分量。
本研究首先测试织物样本的面密度、弯曲刚度、弯曲滞后矩、剪切刚度、剪切滞后矩;以测得的5种指标作为样本的特征分量,构造模糊相似矩阵R;然后,对R的每一行元素从大到小排序,以该排序结果作为真值对1.3节和1.4节的织物匹配结果进行评价。
2 结果与讨论
2.1 悬垂织物的曲率统计直方图
3种性能各异的悬垂织物与曲率统计直方图如图5所示。其中3种织物的规格如表1所示。
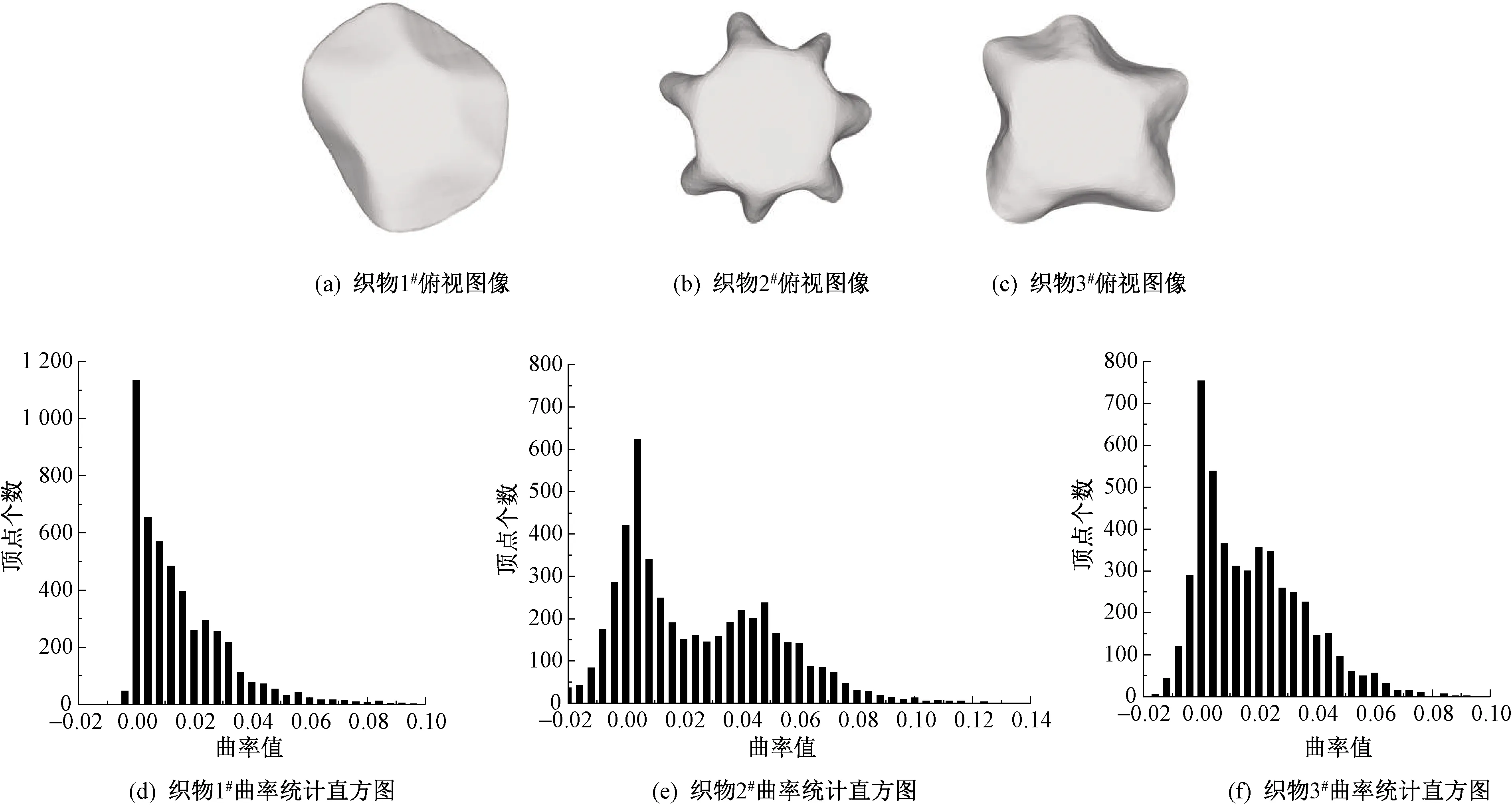
图5 悬垂织物俯视图像与对应的曲率统计直方图Fig.5 Top view images of fabric 1#(a), 2#(b), and 3#(c) and statistical histograms of curvatures of draped fabric 1#(d), 2#(e), and 3#(f)
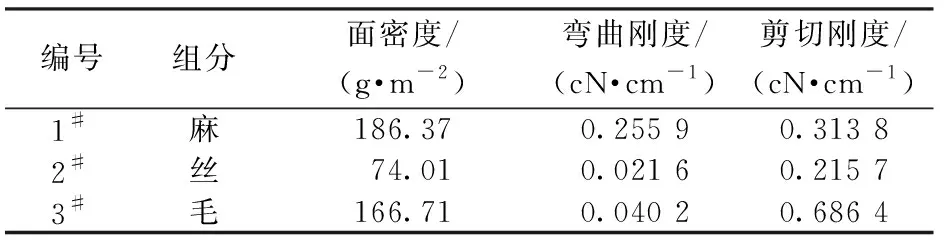
表1 3种织物规格参数Tab.1 Specification of three fabrics
由图可知,3种织物的曲率直方图的峰值均在横坐标的零刻度线上,这是由于织物与支撑圆盘接触部分始终保持平铺状态。织物1#具有较差的悬垂性能,不易变形,因此织物1#在稳定的织物悬垂状态下,悬垂织物三维模型的曲率均值较小;织物2#具有优美的悬垂形态,因此悬垂织物三维模型的曲率分布较为均匀;织物3#虽然也具有较好的悬垂性能,但是其比较挺阔,因此整个三维模型中变形程度较大的部分非常少,该结果与图5(f)中曲率值均小于0.9相互印证。另外,重采样悬垂模型具有相同的顶点数目,统计得到的曲率直方图具有可比性。这种将悬垂形态特征量化的方法为织物悬垂性能的对比分析提供了便利。
2.2 悬垂织物匹配结果
织物匹配结果如图6所示,其中编号1#、2#、3#、4#分别代表4种不同的给定织物,其规格如表2所示。

图6 织物匹配结果Fig.6 Results of fabric matching. (a) Given fabrics; (b) Matching results based on drape indicators; (c) Matching results based on statistical histogram of curvatures of draped fabric
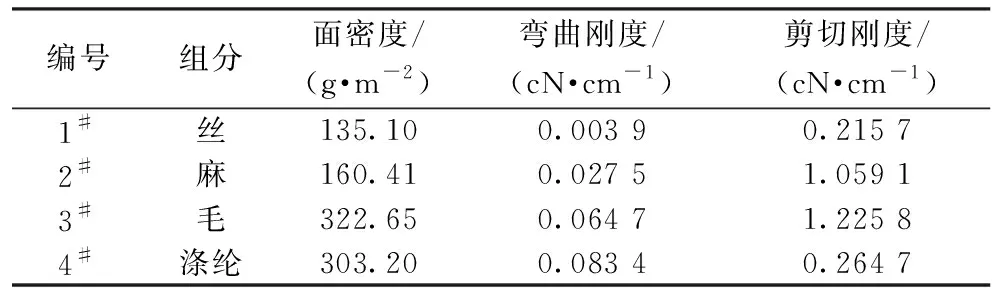
表2 4种织物规格参数Tab.2 Specification of four fabrics
由图6可知,2种情况下,最佳匹配结果与给定织物均具有相似的悬垂形态,不仅体现在织物悬垂轮廓,而且织物悬垂模型的局部弯曲情况也具有相近的分布。该结果说明本研究采用的2种基于悬垂织物三维模型的织物匹配方法均能够兼顾织物的面密度和织物的总体悬垂性能。
在客观评价方面,按照1.5节提出的评价方法,基于悬垂指标和织物面密度的织物匹配方法准确率为86.91%;基于悬垂模型曲率统计直方图和织物面密度的织物匹配方法准确率为93.79%。产生这种结果的原因是:3组悬垂指标和织物面密度的织物匹配方法,对悬垂织物的悬垂系数、波峰数目等指标严格要求,但悬垂织物的离散性使得同一种织物在相同的实验条件下多次悬垂实验结果不唯一,即同种织物可能具有多种悬垂形态,不同织物可能具有相同的悬垂形态。而且3组悬垂指标均是根据织物悬垂形态提取的高级抽象特征,离散的悬垂结果导致波动的悬垂指标;悬垂织物的曲率统计直方图是悬垂织物三维模型的表面变形程度统计结果,未经过抽象处理,而且悬垂模型局部变形是力学性能的直观体现。因此通过比较悬垂织物的局部变形程度可更加深刻地对比织物的力学属性。综上所述,基于曲率统计直方图和织物面密度的织物匹配方法能够从织物的综合悬垂性能方面对织物进行比较,具有一定的应用价值。
3 结 论
本文针对三维扫描采集的三维悬垂模型提出基于局部线性嵌入的悬垂织物三维网格重采样方法,将不同的悬垂织物三维模型用具有相同顶点数目和拓扑结构的三角形网格表示;同时提出了以悬垂织物的局部曲率统计直方图向量结合织物面密度实现织物匹配的方法。
1)本文提出的悬垂模型重采样方法能够将不同形态的三维悬垂模型采样,统一成相同顶点数目和三角形拓扑结构,这对于织物悬垂模型的对比分析具有非常重要的意义。
2)本文提出的基于悬垂模型和织物面密度的织物匹配方法能够从多个织物样本中找到与给定织物性能相近的织物;并且基于悬垂模型曲率统计直方图和织物面密度的织物匹配结果要优于基于悬垂模型和织物面密度的织物匹配结果。本文提出的织物匹配方法可以在不测量织物力学性能、不用手触摸织物的情况下找到与给定织物类似的面料样本,因此具有较高的应用价值,可以为服装设计师和面料设计从业者选择面料提供参考。

