柴油机多元信号自适应分解方法比较

顾程，乔新勇，靳莹，韩立军

(1.陆军装甲兵学院车辆工程系,北京 100072；2.武警工程大学乌鲁木齐校区,新疆 乌鲁木齐 830049)

柴油机作为我军现役装甲车辆的主要动力来源，其状态直接影响装备的作战性能[1]。目前，振动信号由于容易获取、可实现不解体检测等优点，被广泛用于诊断柴油机的技术状态[2-4]。然而特殊的工作性质导致装甲车辆柴油机工作条件艰苦、工作环境恶劣，常常出现几个故障并发的复合故障，仅利用单一通道故障信号无法准确、全面地描述故障特征。随着传感器技术的发展，多传感器多通道同步采集的方式逐步发展起来，多元信号自适应分解方法应运而生[5-7]。多元信号能够反映机械设备更多的信息，一定程度上消除信息的不确定性，能够有效提高信息的可靠性。

针对多元信号的处理，T. Tanka等[8]提出复数经验模态分解(Complex Empirical Mode Decomposition，CEMD)，实质上是对复数据的实部和虚部分别利用经验模态分解(EMD)进行分解；G. Rilling等[9]根据复数据实部和虚部的相关性提出二元经验模态分解(Bivariate Empirical Mode Decomposition，BEMD)，使分解得到的各层分量都具有实际的物理意义；2010年，Rehman等[10]提出三元经验模态分解(Trivariate Empirical Mode Decomposition，TEMD)，将EMD应用扩展到三维信号。随后，Rehman等将多元信号投影到多维空间超球面方向向量，提出多元经验模态分解(Multivariate Empirical Mode Decomposition，MEMD)，实现了多元数据联合分析、同步处理[11]。MEMD的提出解决了多通道本征模函数(IMF)在数量不匹配、在尺度上排列紊乱的问题，但与EMD相同，也存在端点效应、模态混叠等问题。Mandic等[12]提出噪声辅助多元经验模态分解(Noise Assisted Multivariate Empirical Mode Decomposition，NAMEMD)，通过添加高斯白噪声作为辅助信道，一定程度上减轻了模态混叠问题。

针对多元信号在分解过程中的不足，Rehman等[13]在2019年提出了多元变分模态分解(Multivariate Variational Mode Decomposition，MVMD)，通过构造变分优化问题，提取包含在多元信号中固有的多元调制振荡，有效抑制了端点效应、避免了模态混叠，且具有坚实的理论基础。

本研究将MVMD应用于柴油机多通道振动信号分析，通过构建多分量调制仿真信号，利用MEMD、NAMEMD以及MVMD对仿真信号进行分解，比较了三种信号分解效果和分解时间上的差异，并将MVMD应用于柴油机失火故障特征提取，结合支持向量机实现故障诊断。

1 多元变分模态分解

多元变分模态分解是基于变分模态分解(VMD)理论[14]提出的，实现了VMD从一维信号到多元信号扩展，本质上将多元非平稳信号分解成一系列本征模态分量组。

(1)

式中：ai(t)和φi(t)分别为第i个信号分量对应的振幅和相位函数。

对u(t)的每个分量进行Hilbert变换获得u(t)的解析：

(2)

因此，原始实信号向量为u+(t)的实部，即

u(t)=R{u+(t)}。

(3)

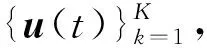
(4)

在上面的模型中有多个对应多元信号维数的线性等式约束，相应的增广拉格朗日表达式变成式(5)。

(5)

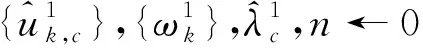
repeat

n←n+1

fork=1:Kdo

end for

end for

fork=1:Kdo 更新中心频率ωk:

end for

forc=1:Cdo 更新λc:

for allω≥0

end for

2 仿真试验分析

2.1 构建仿真信号

柴油机内部结构复杂、零部件众多，且激励源振动需要经过一定的路径到达传感器，通常采集到的振动信号都是非线性非平稳调制信号。柴油机故障会影响振动信号的频率分布，如何提取特征频率的变化是识别故障的关键。仿真试验中，在参考文献[16]的基础上，根据实际工况分别设置调幅信号x1、调频信号x2和谐波信号x3模拟柴油机原始信号，如式(6)～式(8)所示。其中，f1=15 Hz，f2=100 Hz，f3=80 Hz，f4=10 Hz，f5=50 Hz。

x1=[1+cos(2πf1t)]sin(2πf2t)，

(6)

x2=sin(2πf3t+cos(2πf4t))，

(7)

x3=cos(2πf5t)。

(8)

在实际采集过程中，考虑到不同位置传感器采集信号传递路径的差异和噪声的干扰，分别对三个原始信号加以不同幅值的权值，并通过添加白噪声模拟实际信号，其中三个通道的噪声为均值为0、标准差为0.1的随机高斯白噪声。多个传感器采集到的多元仿真信号如式(9)～式(11)所示。

s1(t)=0.6x1(t)+x2(t)+0.9x3(t)+n1，

(9)

s2(t)=x1(t)+x2(t)+0.7x3(t)+n2，

(10)

s3(t)=0.7x1(t)+1.2x2(t)+0.8x3(t)+n3。

(11)

仿真信号的时域和频域波形如图1所示。从图中可以看出，三个通道信号时域信号较为杂乱，无法找出内在规律，频域波形中出现多个峰值，仿真信号的特征频率成分均有所体现，但边频带幅值较高，特征频率不清晰。

图1 仿真信号时频域波形

2.2 性能对比

分别利用MEMD、NAMEMD和MVMD对仿真信号进行分解。其中，在NAMEMD中，将与原信号具有相同长度的2个信道高斯白噪声信号添加到仿真信号中参与分解，以期减轻模态混叠，突出特征频率；在MVMD中，分解层数设置为4，惩罚因子设置为2 000，进行分解。

MEMD分解得到12组IMF分量，通过频谱分析得出，特征频率主要分布在第4～6阶IMF组中，因此第4～6阶IMF组为特征IMF组，其时域、频域波形如图2所示。NAMEMD分解得到12组IMF分量，通过频谱分析得出，特征频率主要分布在第4～6阶IMF组中，因此第4～6阶IMF组为特征IMF组，其时域、频域波形如图3所示。MVMD分解得到4组IMF分量，通过频谱分析得出，特征频率主要分布在前3阶IMF组中，因此前3阶IMF组为特征IMF组，其时域、频域波形如图4所示。

从图2至图4的频域波形可以看出，MEMD、NAMEMD、MVMD均能对多元仿真信号进行自适应分解，得到能够反映特征频率的IMF分量，且不同信道的同一频率成分在同阶IMF中体现，即模式对齐。在MEMD分解得到的特征IMF组中，模态混叠现象较为严重，且边频带幅值较大，有明显的噪声成分。特征频率f3同时出现在第4、5阶特征IMF组中，特征频率f5同时出现在第5、6阶特征IMF组中，调幅信号x1、调频信号x2的边频带明显，且影响到谐波信号x3，在IMF6中出现35 Hz(f5-f1)频率成分。在NAMEMD分解得到的特征IMF组中，因添加了2个信道的噪声同时参与分解，噪声成分有所改善，削弱了分解过程中的模态混叠现象，特征频率较MEMD相对突出，但没有完全克服MEMD的不足。在MVMD分解得到的特征IMF组中，前3阶IMF组分别体现了x3、x2、x1的频率成分，特征频率的幅值更为清晰明显，克服了模态混叠现象，仅存在部分幅值较小的边频带成分，噪声信号基本消失。MEMD和NAMEMD在分解过程中均存在不同程度的模态混叠，导致特征频率并不明显，进而影响柴油机的故障识别，MVMD能够有效地克服上述情况，准确提取特征频率，实现故障诊断。目前故障诊断向着在线化、实时化的趋势发展，对比三种算法的计算时间得出，MVMD的计算时间更短，计算效率更高，能够实现在线诊断、实时监测，有效地提高诊断效率，也为实现柴油机早期故障及时预警提供技术支撑。

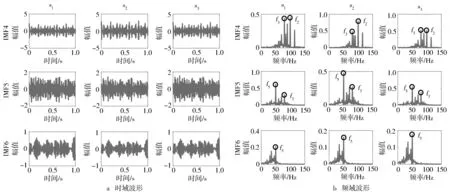
图3 NAMEMD分解后第4～6阶IMF组时频域波形

图4 MVMD分解后第1～3阶IMF组时频域波形

三种算法的计算时间如表1所示。

表1 三种算法分解时间对比

3 台架试验分析

在某型坦克柴油机台架上，通过断开高压油管与喷油器之间连接的方式模拟气缸失火故障。分别设置柴油机正常状态、单缸失火(左1缸失火)、多缸连续失火(左1缸和右6缸同时失火)和多缸间隔失火(左1缸和左4缸同时失火)四种状态。考虑到柴油机激励源及振动信号的传递路径，分别在柴油机两排缸的两端布置4个测点进行信号采集，即左1缸缸头、左6缸缸头、右1缸缸头和右6缸缸头，分别对应测点1至测点4(见图5)。试验时，柴油机运行工况为2 200 r/min、空载，采样频率为20 kHz，采样时间为0.5 s，每种状态采集44组振动信号。

图5 柴油机4个测点位置

以单缸失火故障为例，对四个通道的振动信号进行多元变分模态分解。在分解过程中，首先需要确定分解层数K，不同的K值对分解效果影响较大，取值过大或过小会造成信号欠分解或过分解的情况，影响后续分析。为确定合适的K值，K分别选取3，4，5，6，对44组信号进行分解，不同K值下44组样本中心频率分布如图6所示。从图中可以看出，当K<4时，属于欠分解情况，当K>4时，中心频率波形出现较为剧烈的振荡或分量间出现中心频率相近的现象，属于过分解情况，因此单缸失火故障时，选取分解层数K=4较为合适。柴油机单缸失火状态下，多通道振动信号在K=4时MVMD分解结果如图7所示。经分析，正常状态、多缸连续失火和多缸间断失火状态的最佳分解层数均为4。

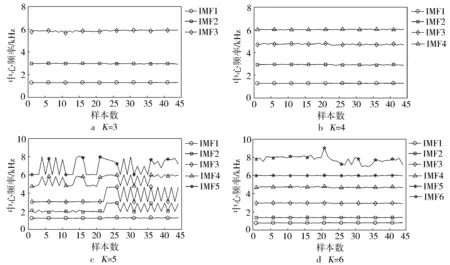
图6 不同K值下44组样本中心频率分布

图7 左1缸失火状态下，振动信号MVMD分解结果

柴油机出现失火故障时，由于激励源产生的激励发生改变，振动信号的能量也会发生变化，且不同失火故障对各测点不同频段的影响程度也不同。因此，考虑从能量角度出发，计算4个测点不同频段的能量作为特征参数，输入到支持向量机模型(SVM)中进行模式识别。

表2示出不同状态下各测点4个IMF分量的能量值。正常状态、单缸失火故障、多缸连续失火故障和多缸间隔失火故障的类别标签分别为1、2、3、4，从44组样本中随机选取20组为训练集，其他24组为测试集，将4个测点经MVMD分解后的4个IMF分量能量值作为特征参数输入到SVM中，选择RBF核函数进行故障诊断，训练结果和测试结果如图8所示。从图中可以看出，训练样本和测试样本的准确率都达到了100%。

表2 不同状态下各测点4个IMF分量的能量值

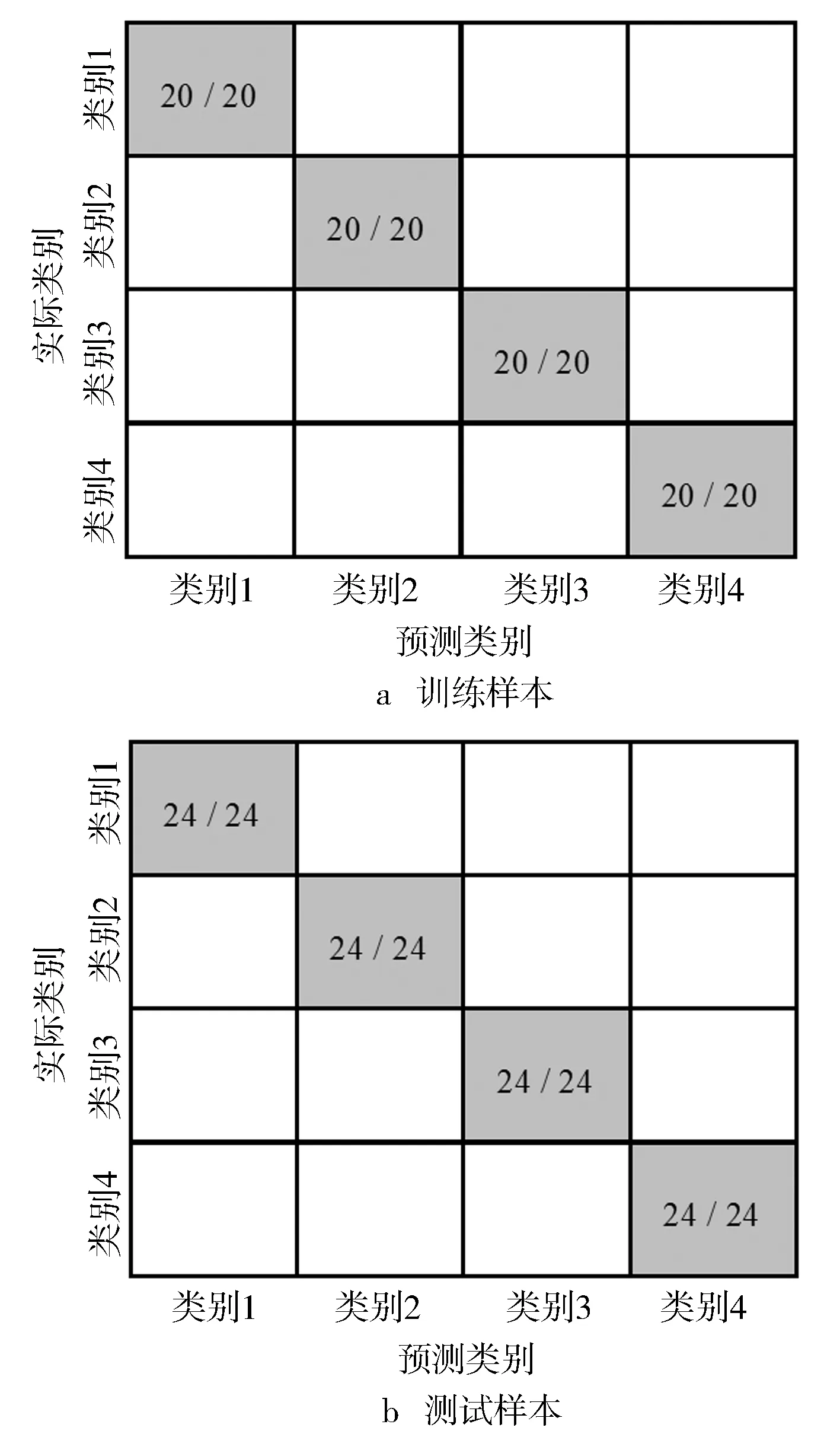
图8 SVM训练和测试结果

为体现MVMD算法的优越性，本研究同时利用MEMD和NAMEMD对实测振动信号进行自适应分解，其中为NAMEMD中添加两信道的高斯白噪声信号。分别提取4个测点中与原始振动信号相关系数较高的前4阶IMF分量，即IMF1～IMF4，计算其能量值作为特征参数，并输入到相同的分类器中进行故障识别。结果显示，利用MEMD算法训练样本和测试样本的准确率分别为95%和87.5%，利用NAMEMD算法训练样本和测试样本的准确率分别为100%和95.8%，准确率均低于MVMD算法，表明运用MVMD分解得到各分量的能量值可以作为故障特征参数，对不同类型失火故障能够实现有效的识别，在其他类型故障或者多类型耦合故障是否有效还需要进一步研究。

4 结论

本研究将MVMD引入到机械故障诊断领域，利用仿真试验和台架试验对MVMD自适应分解柴油机多元振动信号进行研究，得出如下结论：

a) MVMD能够有效提取多分量调制信号中的特征频率，在抑制模态混叠和端点效应方面表现突出，且分解效率较高，分解效果优于MEMD和NAMEMD；

b) 利用MVMD对4个通道柴油机振动信号进行分解，以每层分量能量分布作为故障特征输入到支持向量机进行故障识别，训练集和测试集的识别率均达到100%；

c) 不同位置激励的变化对多个测点的影响程度不同，多元信号包含的机械设备的信息更为全面，更适应于状态评估和故障诊断，多元信号自适应分解应用前景广泛。