在解析几何教学中渗透数学思想方法的策略研究

赵雪梅

(江苏省宜兴丁蜀高级中学 214221)

众所周知，解析几何是高中数学的重要分枝.解析几何部分蕴含着丰富的数学思想，该部分的主要知识点通过这些数学思想串联在一起，贯穿着整个解析几何的学习过程.如果说在解析几何教学中知识是载体的话，那么数学思想方法就是精髓和灵魂，只有让学生掌握了这些数学思想方法，学生才能够灵活应用解析几何知识来解决解析几何问题，才能够提高解析几何教学效果.

一、借助数学史，渗透数学思想方法

数学史浓缩了人类数学发展的主要过程，概括了数学知识的本质，提炼了重要的数学概念和数学思想，是学生乐于知晓尤感兴趣的话题，更是学生理解和掌握数学思想方法的重要源头.作为数学教师，我们可以通过引入数学史的方式来向学生渗透数学思想，使其为数学课堂教学服务.为此，我们可在解析几何知识的起始环节的教学中，适当引入笛卡尔有关直角坐标系的创立史，形象直观地让学生了解解析几何的相关发展背景，从而激起学生强烈的学习兴趣，为数学方法的学习奠定基础.例如，在学习解析几何之前，先设置一个导言课，通过讲座和师生交流的方式，来介绍解析几何课程内容和学科思想方法.我们可以从介绍笛卡尔入手，让学生置身笛卡尔当时所处的历史时代及创立解析几何的构思背景，在了解解析几何的创新历程和巨大的应用价值中，体会笛卡尔的精神、信念.在解析几何教学中引入数学史，并将其以“问题化”的形式展开教学，不仅使得数学史在解析几何课堂中的引入更加自然，还有助于学生去体会数学思想，培养学生的数学核心素养.

二、通过代数与几何之间的转化，体会数学思想

用解几处理问题的本质就是几何问题代数化，通过建立坐标系将几何问题转化为代数问题去求解，这是数形转化的绝佳平台.在现阶段的高中数学解析几何教学中，很多教师仅注重传授学生将几何问题转化为代数问题的方法，很少去引导学生探究代数结果背后的几何意义，这样的教学导致学生对数学思想方法的理解不到位.教师应该让学生明白，用解析几何思想处理研究具体问题，必须具备两种本领：一是化数为形，二是由形逆数.化数为形是指将代数问题转化为几何结构，这样兼顾了问题的直观性；由形逆数是指通过恰当建系将几何结构代数化，使几何问题更具微观概括性.让学生在数形转换的奥妙中去体会数学思想.例如：在椭圆部分的教学中，教师先出示椭圆的实物模型，帮助学生建立椭圆的直观感知，然后再利用代数表达式去揭示椭圆图形的几何性质，总结椭圆的定义.接着要积极引导学生探究椭圆的标准方程，和学过的什么曲线方程形式比较接近?让学生将之与圆的标准方程进行对比，它们有何异同?让学生体会数学思想方法的应用.互动过程如下：

不妨设M为椭圆上的任一点，M到两焦点F1和F2的距离之和用2a表示，同时设椭圆的焦距为2c(c>0)，如此一来，焦点F1(-c，0)、F2(c,0).

那么该椭圆就是集合P={M||MF1|+|MF2|=2a}.

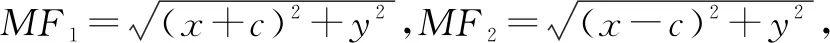
教师提出问题引导：通过观察圆的标准方程，两边开方，我们能够非常明显的发现它的几何意义：等式左边是表示某两点间距离，右边则是距离值.但我们再观察椭圆的标准方程，就会发现它的几何意义并不明显.通过椭圆的标准方程，我们很难发现“椭圆上的点到两定点的距离之和均等于2a”这一几何意义.接下来教师就要引导学生分析上述推导过程，寻找代数推理过程中的几何意义.

通过这样的课堂教学，学生不仅体会到了代数与几何间的相互转化，也感受到转化并非一帆风顺，有时是相当艰难，只有心中具备转化执念，熟悉不同距离的代数表达，勇于探索，敢于尝试，才能体会成功的快乐.

三、借助思维导图进行复习，帮助学生提炼数学思想方法

学生通过大量的知识学习，已经接触到了部分数学思想方法，教师要及时地组织学生进行复习，这样学生才不会遗忘，才能够将其内化成自己的思维方式.思维导图能够将学生所学知识之间的逻辑关系可视化，是引导学生高效复习的一种非常有效的手段.它能够将各个概念之间的关系直观地表达出来，能够调动学生的思维，促进学生将所学的知识联系起来形成知识体系，让他们由被动地接受知识转化为主动地去构建知识体系.

思维导图不仅能够辅助学生构建知识体系，提炼数学方法，还能够应用于解题当中，锻炼数学思维，如下图所示：

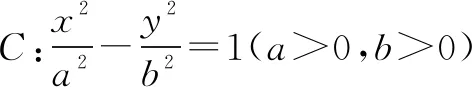
客观地说，解析几何的相关部分内容繁琐，运算量大，思维要求较高，既是教学的重点，也是教学的难点，更是高考的热点.由于其自身知识抽象性和综合性较强，也成为了很多学生学习的难点.数学思想作为贯穿整个解析几何教学的思想方法，它能够将这些零散繁琐的知识点串联起来，形成知识体系.我们在平时的教学中，要把这些数学思想自始至终地让学生感受体会，于润物细无声中提升学生思维能力.