绗缝机花样加工代码自动生成算法
李 亮, 倪俊芳
(苏州大学 机电工程学院, 江苏 苏州 215021)
花型样条加工代码通常是由花样设计者以直线、圆弧、样条曲线等基本线条通过移动、复制、镜像、旋转等操作绘制出图形轮廓,再通过逼近、插补等算法的转化,得到的可用于绗缝机或特定数控系统的加工代码[1-2],可直接用于床垫、床罩、棉被等织物的绗缝加工。花样描制算法[3]即通过上述操作对目标绗缝图像进行描摹绘制,从而使图像轮廓作为加工路径,将面料、填充料、底料缝制在一起,实现外层布料与填充料之间的相对固定,同时增加绗缝制品的立体感与美感。该方法可大大降低花样设计的难度,减少人工成本,且可保存花样以便后续使用;但其也存在因描制图样尺寸过大、形状不规则、花样过复杂的缺点,导致描制速度过慢,且受操作者的经验影响较大,常常难以加工出高质量花样。为了解决上述方法的不足,基于图形矢量化方法的花样自动生成算法应运而生,其核心思想是提取目标图像的图元,以基本线条进行分段拟合,从而得出相应花样及加工代码。Bezier、NURBS、B样条等复杂曲线被提出以精确表达高次曲线[4-5],然而目前大多数的数控系统仍不支持上述曲线插补,故绗缝加工系统仍采用将加工路径离散为微段直线和圆弧的插补方法[6-7]。
国内学者[8-9]研究了在保证图像不失真的条件下,提取图像基本图元进行曲线拟合,实现图形的矢量化,并取得了一定进展。其方法通常分为2类:1)先获取轮廓上的基元,即优先恢复的方法;2)先抽取基元间的分界点,即优先分割的方法。前者注重分割质量,但拟合速度慢;后者则更注重效率。分界点即角点,在保留图像重要特征的同时,可以有效地减少数据量,提高计算速度,使图像的实时处理成为可能,同时角点在加工时,可视为加工微段基元的起末端点。现有多种角点检测方法[10],如:基于曲率计算的方法,其计算量小,但易受到噪声影响,产生假角点;基于小波变换的角点检测方法,其抗干扰能力强,但计算量大且复杂;基于灰度图像的角点检测方法,如Harris角点检测方法,在检测时,设置阈值过大会导致伪角点的产生,阈值过小则导致遗失角点。为此,本文基于遗传算法(GA)[11],获取绗缝图像轮廓信息以生成对应二进制数组作为初始种群,其中每行二进制数列都是对加工路径的表达;设定微段基元上各坐标点的位移偏差之和为误差函数,并将拟合总误差和拟合段数作为每条加工路径的适应度函数的参量;通过选取合适的选择、交叉、变异算子,在初始种群的不断进化下得到最优染色体,即为角点的分布与角点间的微段基元属性,也即绗缝花样的最优加工路径;并将各微段基元直接转化为G代码,从而将采集的图像转化生成加工代码,加工出复杂花样,以满足绗缝领域的自动化加工需求。
1 绗缝图像轮廓追踪及优化
采集到的图像无法直接被用于遗传算法以进行轮廓拟合,因此,首先需要对图像进行轮廓追踪以获取关键信息。
在图像采集过程中,由于光照等因素影响会降低图像质量,即需要对所采集的图像进行预处理。将任选摄影类图像经过滤波、形态学操作和Canny算子处理后,得到边缘点阵图像,如图1所示。采用Freeman链码[12]的方法检索边缘轮廓,将其追踪为若干条携带坐标信息的有序数据点链,但其边缘轮廓存在孤立点、毛刺点、断点的问题(见图2),且在绗缝加工中,奇异点会被认作边界点,从而执行剪线和跳针操作,不但增加了加工的复杂性,同时影响产品的美观性,因而需要对细节及冗余信息处理以优化绗缝织物质量。
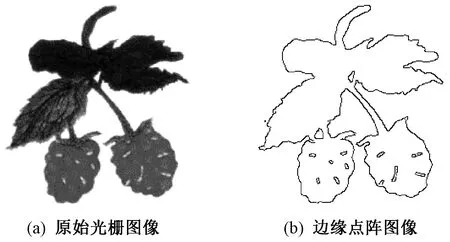
图1 图像预处理Fig.1 Image preprocessing
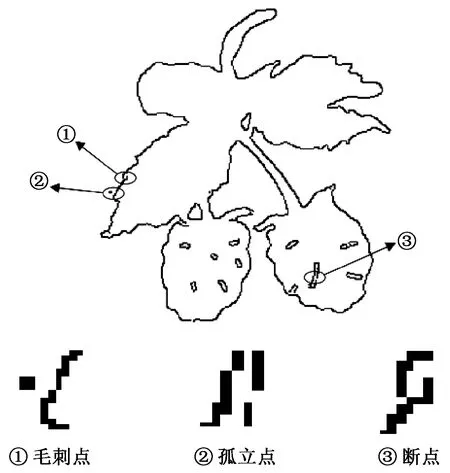
图2 奇异点Fig.2 Singular points
本文所改进的轮廓追踪算法是:被寻访过的点不会被立即取为背景色,而是在整条轮廓都被寻访到后执行,因而单个像素点可以被不止1次地访问。为避免如2个像素点间的来回寻访,规定下一次寻访方向是使得本次寻访点为最末寻访方向的相反方向,且使用的Freeman链码方法为8邻域方法。图3示出轮廓追4条点链:外闭合轮廓1、短分支轮廓2、长分支轮廓3和内闭合轮廓4,避免了因拓扑关系过复杂而造成的错误分割。算法流程图如图4所示。

图3 轮廓追踪算法实例Fig.3 Example of contour tracking algorithm.(a) Test bitmap image;(b) Segmentation results
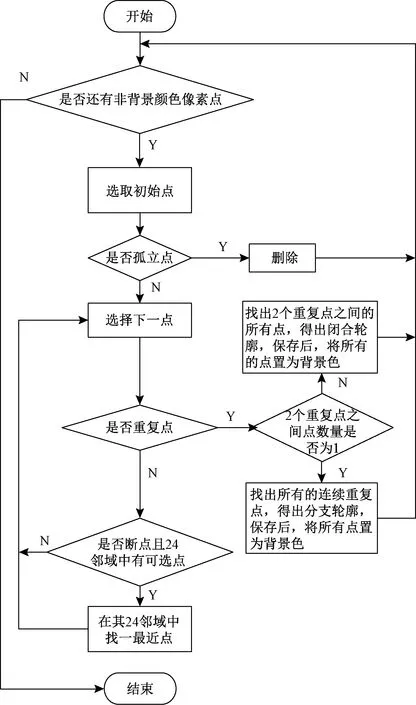
图4 轮廓追踪算法流程图Fig.4 Flow chart of contour tracking algorithm
2 基于GA以微段基元拟合绗缝轮廓
针对提取出的点链轮廓,以直线和圆弧作为微段加工基元进行拟合,确定遗传算法方案,通过进化的思想迭代出最优染色体,即为最优的绗缝花样曲线加工路径。
2.1 初始加工路径组的生成
设N为通过轮廓追踪算法从目标绗缝图像中得到的一条待拟合点链,并定义为
N={p1(x1,y1),p2(x2,y2),…,
pn-1(xn-1,yn-1),pn(xn,yn)}
其中(x1,y1),(x2,y2),…,(xn-1,yn-1),(xn,yn)是该绗缝图像上对应点的坐标。点链中的点可分为微段加工直线或加工圆弧的端点和端点之间的连续点2种,采用二进制编码表达染色体,当染色体基因为1时,该坐标点为微段基元端点;否则该点为端点间连续点。此时,每条二进制染色体数列就是对应加工路径的描述。
染色体长度L:染色体的长度为点链的长度n。种群规模M:取L/4作为加工路径总数。随机生成长度为L,宽度为M的二进制数组为初始加工路径组。
2.2 控制参数的确定
2.2.1 微段加工基元误差函数
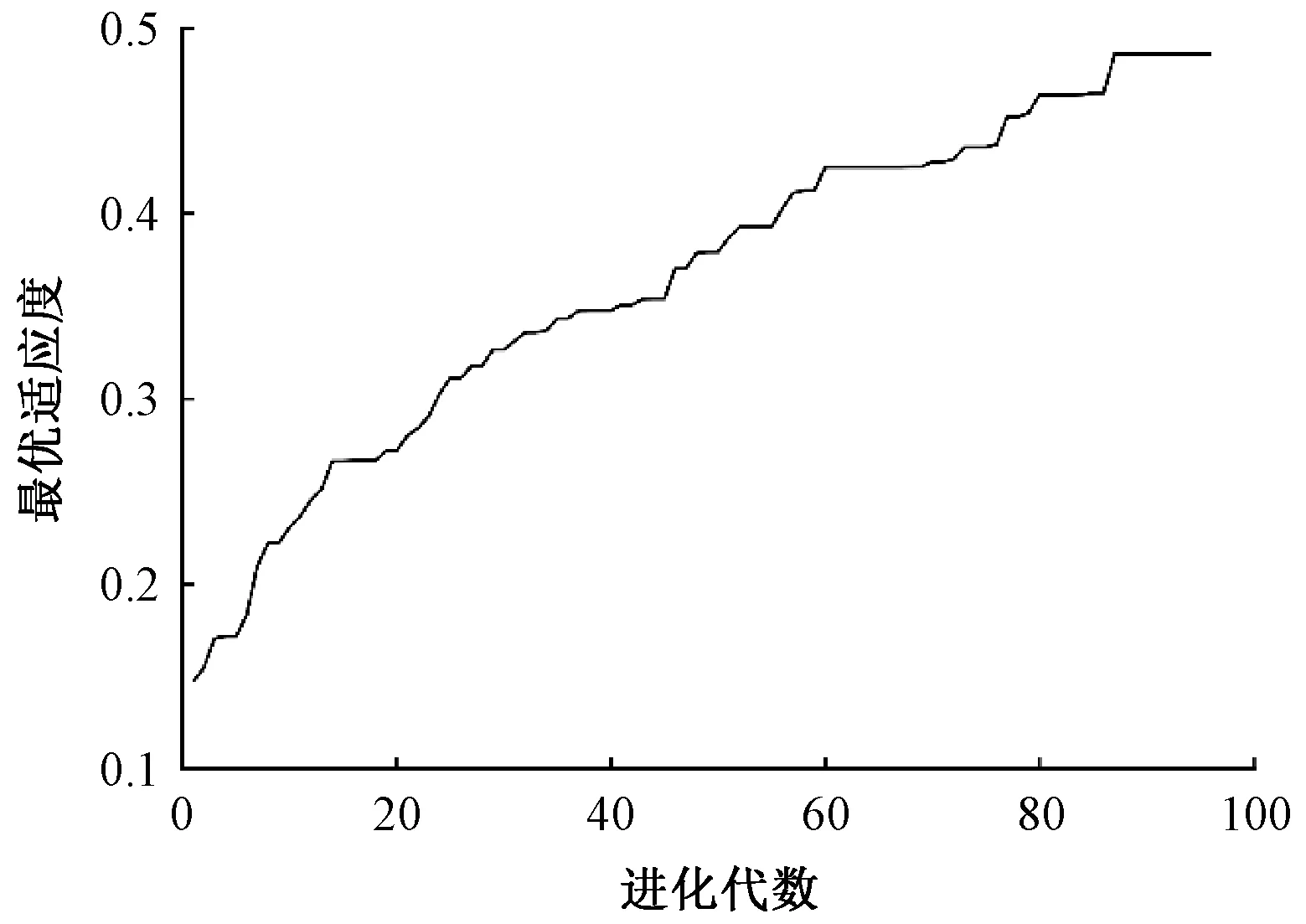
设Pi,Pm(1≤i 对于直线加工拟合,确定直线函数为 Y=kX+b (1) 式中,k和b为待求参数。 添加2个约束: (2) 式中,xi、yi,xm、ym分别为点pi,pm的横纵坐标。解出k,b,可得直线方程: (3) 则直线位移误差: (4) 式中,yj、Yj分别为拟合前、后点pj的纵坐标。 对于曲线加工拟合,确定误差函数Ec为 Ec=X2+Y2+AX+BY+C (5) 式中,A、B、C为待求参数。 添加2个约束: (6) 此时,求解圆弧加工位移误差的参数问题,变为了求解A、B、C的最优值的问题。化简后得到: (7) 其中,λ1和λ2为常数,从而可得A、B、C的值,并得出圆弧拟合的位移误差Ec。 比较El和aEc(其中a为经验参数,当a大于1时,趋向于拟合为直线;反之则趋向于拟合为圆弧,预设值为1.2),从而将最小误差作为该微段的最终位移误差S(i),并同时将线条属性state.flag和微段基元的其他相关属性保存。输入测试点链数据 [0,0;1,1;1,2;1,3;2,4;3,5;4,5;5,5],拟合结果如图5所示。 图5 微段加工基元拟合结果Fig.5 Base processing element fitting result 2.2.2 加工路径适应度函数 第i条加工路径的适应度值F(i),与加工路径中微段基元的总段数d及该路径的总误差T(i)成反比,则确定其适应度函数为 (8) (9) 式中,b为调整系数,预设值为1.5。 2.2.3 遗传算子 选择概率Ps:选择操作可以保证优秀的加工路径能被保留至子代中,则由轮盘赌的思想,第i条路径的选择概率Ps定义为 (10) 交叉概率Pc:交叉操作可以将2条不同的加工路径从某点交换,从而生产新的路径,取定值为0.3。 变异概率Pm:变异操作通过改变加工路径中部分微段加工基元属性从而保证多样性,取定值为0.1。 2.2.4 终止条件 最优适应度值连续10代不改变时,迭代结束。此时,适应度最高的个体即为最优染色体,也就是目标绗缝花样的最优加工路径。在最优染色体中,值为1的点对应为微段加工基元的端点,端点之间的微段为加工直线或加工圆弧,其具体类型由该微段的各点对应坐标信息决定。 基于MatLab平台编程,对改进轮廓追踪算法得出的图1(b)中的最外层轮廓图样使用遗传算法拟合验证。该轮廓共有1 431个像素点,一共运行到96代,运行时间为51 s,最优加工路径见图6,各代路径的最优适应度见图7。 图6 最优加工路径Fig.6 Optimal processing path 图7 各代最优适应度Fig.7 Optimal fitness of each generation 采用误差函数对对应点链处理后,将代表线条属性的state.flag输出,同时若判定该微段基元为圆弧时,将代表圆弧加工半径大小的state.R输出。根据已有信息,可将直线微段转化为相应的G代码,但仍不能判定圆弧加工的加工方向,即G02与G03的判定。 当起点、终点、圆弧加工半径已知时,圆弧加工的方向问题也即判定圆弧加工路径的优劣弧问题。获取微段基元中点pz(xz,yz),连接起点、中点、终点,通过矢量点积的方法求得矢量夹角,从而判定优劣弧,进而转化为G代码语句。 (11) 将G代码文件导入,采用绗缝机控制器进行模拟加工,加工路径如图8所示。结果表明,图像还原度高,质量高,加工效果好。 图8 绗缝机模拟加工Fig.8 Quilting machine simulation processing 花样自动生成算法相比花样描制算法具有智能化、自动化高的优点,是绗缝机花样制版领域的发展趋势。本文提出了将图像轮廓直接转化为绗缝加工路径的方法,有效地弥补了绗缝加工领域普遍存在的效率低、人工成本高、受经验影响大的不足;改进了轮廓追踪算法,减少了奇异点造成的影响,并将点阵图像分割为若干段有序点链轮廓;通过带约束的最小二乘法作为误差函数,确保了花样的一阶连续,避免了剪线和跳针的影响;使用遗传算法,在选择、交叉、变异算子的作用下,基于适应度函数的指导,经过96代迭代进化,最终代染色体所代表的绗缝加工路径适应度高,拟合段数少。文中对任选摄影类图像进行处理,结果较好,在处理卡通类图像时效果更佳,但处理部分复杂纹理图像时,所取经验参数仍需改进。该算法为图像实时转化为加工代码提供了参考,并在绗缝机上进行了相关实验,结果满足绗缝加工的要求,为刺绣机加工代码的生成提供了依据。

3 实例应用分析
3.1 实验验证

3.2 绗缝机控制器模拟加工

4 结 论

