纬编针织机织针自由状态下固有频率测试方法

戴 宁， 彭来湖， 胡旭东， 崔 英， 钟垚森， 王越峰

(浙江理工大学 浙江省现代纺织装备技术重点实验室， 浙江 杭州 310018)

织针作为纬编针织机重要的编织机构，其在退圈、集圈等高度位置的振动特性与纬编织物的品质密切相关，织针的振动主要来自织针与三角间的相互作用，当三角对织针的激励达到织针固有频率时，导致织针共振，将直接影响退圈、弯纱等工艺动作。近年来，针对织针与三角相关的研究也越来越多，浙江理工大学的张华[1]、武汉纺织大学张成俊[2]等对织针与三角间的相互作用进行了动力学建模并对织针与三角间的冲击和碰撞通过相应的实验进行了验证，但二者对织针的研究主要还停留在刚体运动层面，并未从振动层面对改善织针振动进行研究，而织针自由状态下固有频率测试方法是分析织针振动特性的前提。织针细长、扁平的几何特性可等效为两端自由梁，目前，采用压电陶瓷材料对梁固有频率测试的研究较多，如刘永春[3]、唐治[4]等采用压电陶瓷对悬臂梁固有频率测量及抑振进行了相关研究，但其研究对象结构简单、尺寸较大、且单端固定，而纬编针织机织针尺寸相对微小，对于其在自由状态下固有频率的有效测量具有一定难度。

本文借鉴压电陶瓷测振原理并结合织针自身的结构特点，采用将小矩形PZT薄片贴敷于织针针杆表面，形成PZT、织针黏合体结构。通过阻抗分析仪WK6500B对黏合体进行扫频激励，获取黏合体在宽频范围内复阻抗及相位角的响应特性，当扫频频率达到黏合体固有频率时，黏合体复阻抗及相位角响应曲线出现突变。采用ANSYS有限元仿真软件分析PZT薄片质量对织针固有频率测量误差的大小，并引入悬臂梁曲率理论，对PZT测振方法进行理论指导。本文提出的织针固有频率的测试方法对织针振动理论的研究具有一定意义。

1 研究方法概述

织针是纬编针织机成圈编织机构中重要的编织执行器件，而成圈编织机构性能的优劣直接影响纬编织物的品质。织针沿三角表面做受迫升降运动，纱线在织针上下运动过程中，弯曲成线圈，根据新旧线圈和织针针舌的相对位置，成圈过程可分为起针、退圈、垫纱、闭口、套圈、脱圈、弯纱、成圈以及牵拉阶段，新旧线圈相互串套形成织物[5-7]，纬编针织机编织过程织针运动简图如图1所示。

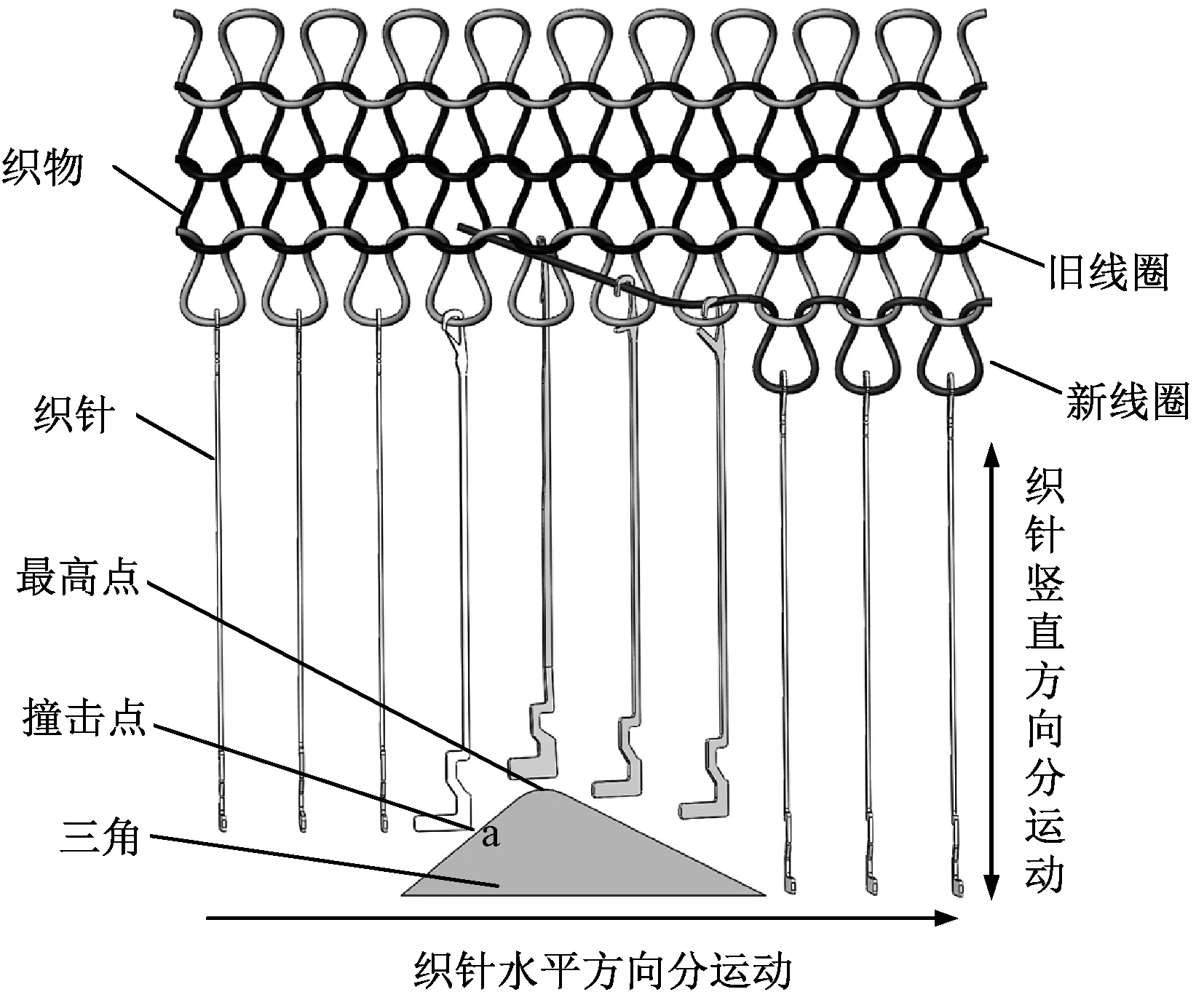
图1 纬编针织机成圈过程织针运动简图Fig.1 Simplified diagram of knitting needle movement during loop forming process of weft knitting machine

由图可知，织针随针筒运转，并与三角表面a点发生撞击后沿三角表面运动，此瞬态撞击过程将引起织针的振动，并且由于织针沿三角表面做受迫运动，三角本身的机械振动也会引起织针的随机振动[8-10]。当织针发生振动时，成圈过程中织针针舌竖直高度与新旧线圈的相对位置发生变化，直接影响织物的成圈效果，形成疵点。研究纬编针织机织针的振动特性对提高其性能的稳定性至关重要，而织针自由状态下的固有频率特性的测量是研究针织振动特性的前提。本文结合织针尺寸及外形特性，应用共振理论，设计了织针固有频率测试方式，并采用ANSYS有限元仿真软件进行分析，对织针固有频率测试方案进行验证，本文总体设计方法如图2所示。

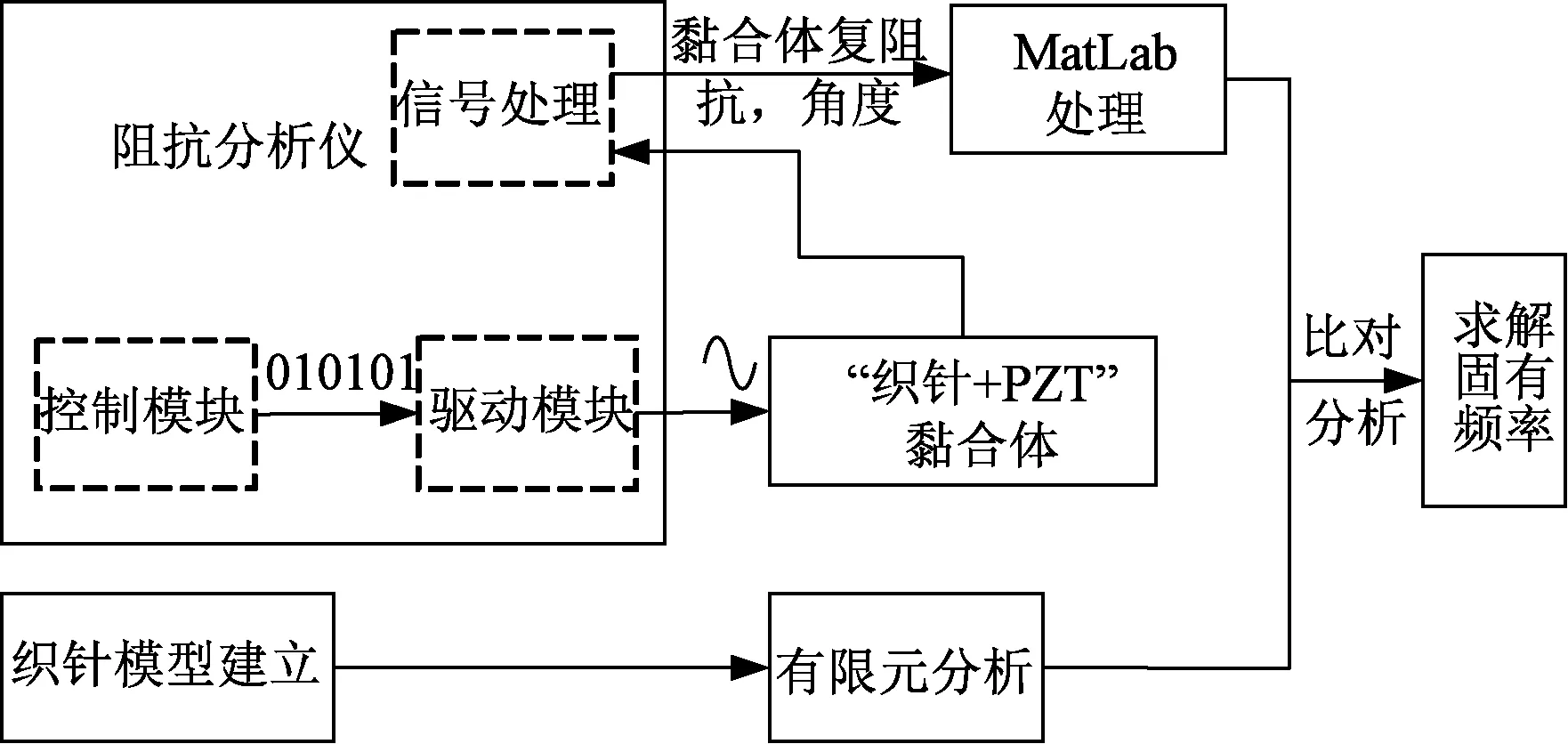
图2 织针固有频率总体设计方案简图Fig.2 Schematic diagram of overall design of the natural frequency of the knitting needle

图2示出织针固有频率总体设计简图，本方案采用将小尺寸PZT薄片粘贴于织针针杆表面形成织针、PZT黏合体，并采用阻抗分析仪内部控制模块设置扫频范围以及扫频信号电压幅值参数，内部驱动模块对扫频信号进行放大后加载于黏合体上，当扫频频率到达黏合体固有频率时，引起黏合体共振，导致黏合体阻抗畸变，PZT压电效应增强，阻抗分析仪对扫频范围内黏合体的阻抗特性变化信号进行处理，产生扫频范围内黏合体的复阻抗以及角度数据，并采用MatLab处理，形成复阻抗-频率，相位角-频率曲线。为了检测测试数据的准确性，采用SolidWorks软件建立织针三维模型，并采用ANSYS软件进行有限元处理，通过对比分析验证测试方案的准确性。

2 实验方法

本文采用阻抗分析仪测试黏合体的固有频率来近似确定织针的固有频率，PZT的额外引入将改变织针原有结构的质量与刚度，故实验要求PZT的质量小，贴敷面积小，贴敷厚度薄，贴敷层无杂质等要求。黏合体剖面结构图如图3所示。

图3 黏合体剖面结构图Fig.3 Cross-section structure of bonded body

采用英国稳科公司(Wayne Kerr)型号为WK6500B的阻抗分析仪对黏合体结构进行阻抗分析，将黏合体上的2条细直导线接入WK6500B阻抗分析仪，实验连接图如图4所示。

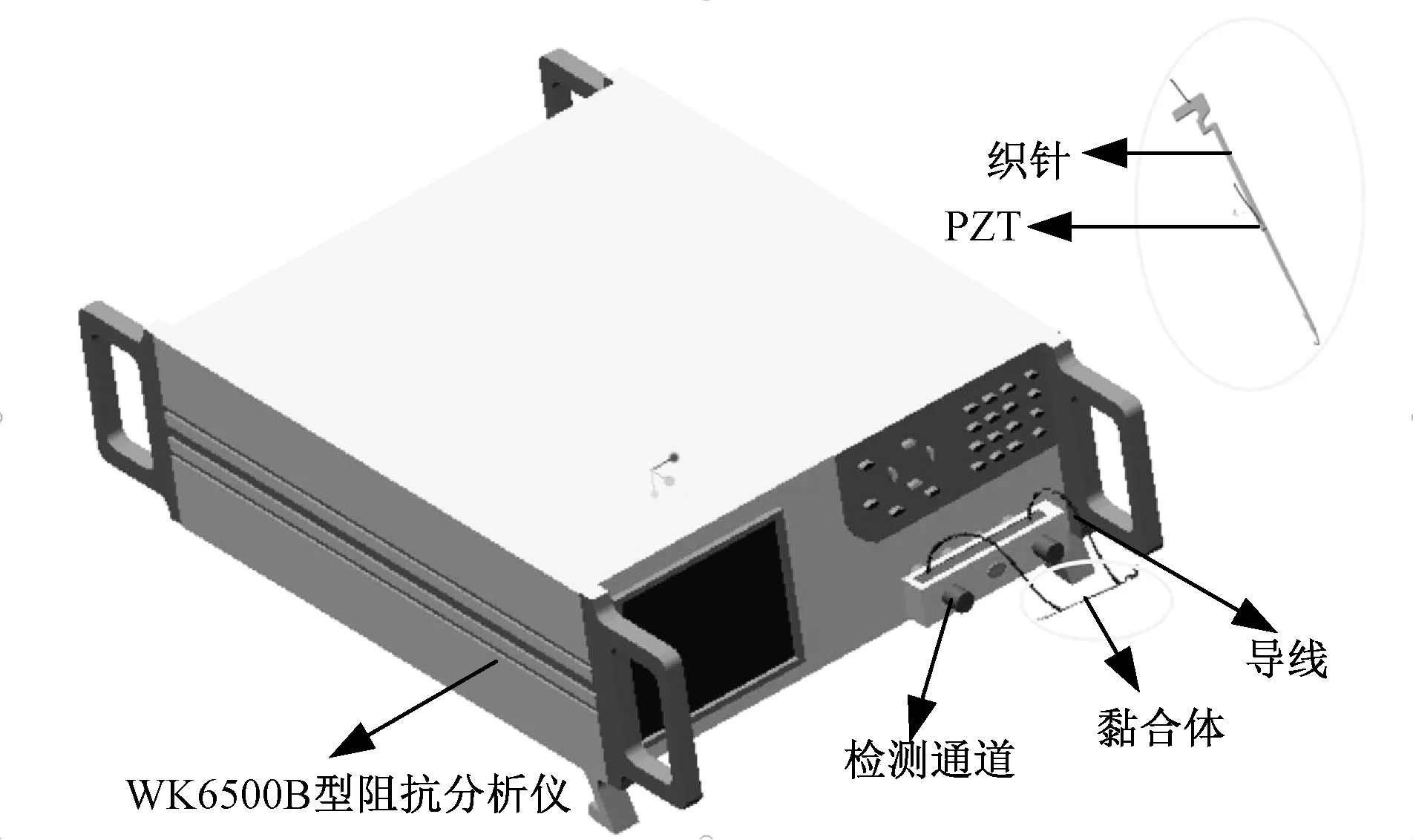
图4 实验连接图Fig.4 Diagram of experimental connection

当对黏合体表面施加交流电场时，由于逆压电效应，PZT产生与交流电场同频率的机械振动，此时与PZT黏合在一起的织针对PZT机械振动产生振动响应，并反作用于PZT。PZT由于正压电效应，使得PZT表面电信号发生变化，并等效为PZT电阻抗发生变化。当交流电频率达到织针固有频率时，织针振动幅度畸变引起PZT电阻抗发生突变，即黏合体复阻抗发生突变。对阻抗分析仪设置合适的扫频范围，进行阻抗分析，引起黏合体复阻抗突变点对应的频率即为黏合体的固有频率，当PZT的质量足够小时，可用黏合体的固有频率近似表示针织的固有频率。阻抗分析仪测量黏合体固有频率原理如图5表示。

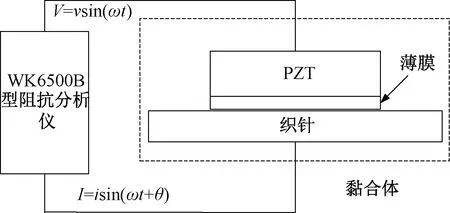
图5 阻抗分析仪测量黏合体固有频率原理Fig.5 Principle of measuring natural frequency of bonded body by impedance analyzer

如图5所示，PZT无间隙粘贴于织针表面形成黏合体，黏合体的机电耦合特性用PZT的机械阻抗Zp代替，其值大小为阻抗分析仪输出的电压V与流入阻抗分析仪的电流I的比值。织针机械阻抗Zn的大小为PZT激振力与织针振动响应速度的比值。黏合体的复阻抗表达式如式(1)所示。

(1)

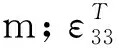
由式(1)可知，PZT与织针的结构特征及PZT的压电特性保持不变，故黏合体的复阻抗与阻抗分析仪交流激励电压的频率有关，当其达到黏合体固有频率时，PZT的机械阻抗Zp发生突变，由公式(1)可得，此时黏合体复阻抗发生突变。故采用阻抗分析仪可正确测量黏合体的固有频率。

设置合适的扫频频率范围以及电压幅值，对黏合体进行阻抗分析，采用MatLab绘制复阻抗-频率，角度-频率曲线并进行分析，如图6所示。

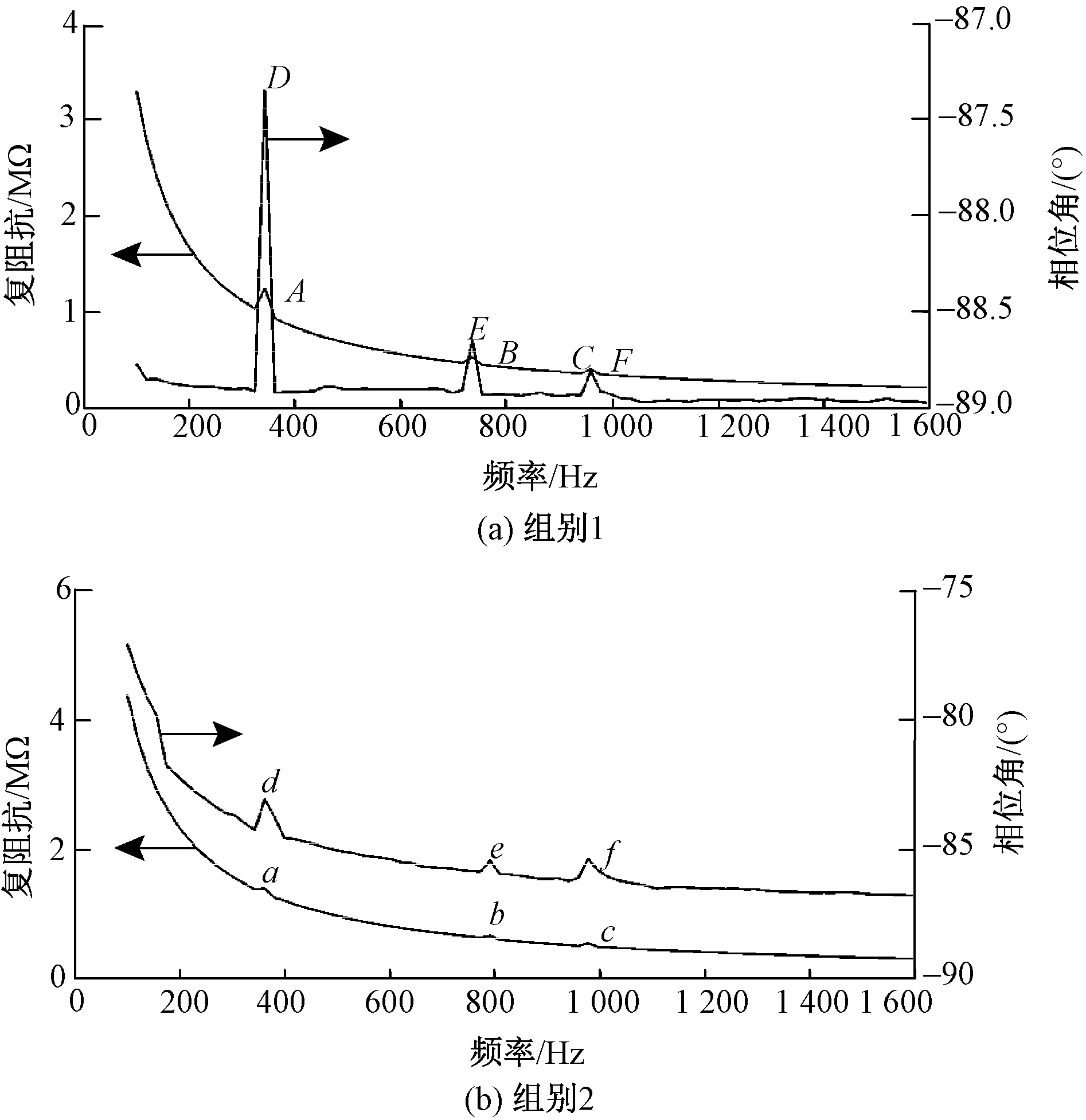
图6 复阻抗-频率与角度-频率曲线图Fig.6 Graph of complex impedance-frequency and angle-frequency. (a) Group 1; (b) Group 2

图6示出2组实验中黏合体的复阻抗-频率与相位角-频率曲线。图6(a)中A、B、C点为复阻抗曲线中3个尖峰点，其横坐标代表的频率值分别为342.4、734.0、957.8 Hz，D、E、F点为相位角曲线中3个尖峰点，其横坐标代表的频率值分别与A、B、C3点的横坐标值相等。图6(b)中a、b、c点为复阻抗曲线中3个尖峰点，其横坐标代表的频率值分别为361.1、790.0、976.5 Hz，d、e、f点为相位角曲线中3个尖峰点，其横坐标代表的频率值分别与a、b、c3点的横坐标值相等。单独分析其中任意一组实验可知，不同频率下的复阻抗以及相位角“尖峰值”存在差别，其值的大小反应了PZT压电特性的强弱程度。织针在不同模态下，同一位置的形变程度存在差异，具体体现在织针形变弯曲下的曲率存在差别，如图7所示。PZT贴于织针表面，PZT压电特性的强弱与织针表面弯曲时曲率值相关。

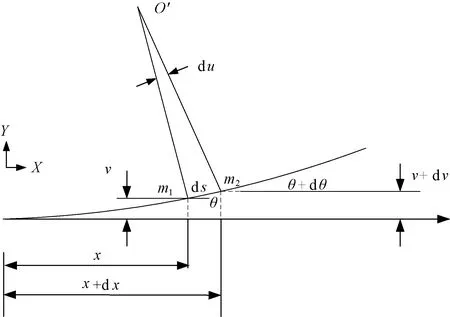
图7 弯曲时织针表面曲率示意图Fig.7 Schematic diagram of surface curvature of knitting needles during bending

图7示出织针表面的曲率示意图，O′表示曲率中心，点m1、点m2为位于织针弯曲面上2点。x、x+dx分别为点m1、点m2的横向位置，单位为m；θ、θ+dθ分别为点m1、点m2的旋转角度，单位为rad；v、v+dv分别为点m1、点m2的挠度，单位为m；ds为点m1、点m2间的弧长，单位为m。故可得曲率：

(2)

各阶模态响应下，织针同一位置处曲率K的大小存在差别，故贴于织针特定位置处的PZT在织针各阶模态响应时表现的压电特性存在差距。从而导致同一组试样下阻抗分析仪中不同频率下的复阻抗以及相位角存在差别。

对比试样1、试样2中各阶模态下的频率，并绘制表格，详细如表1所示。

表1 试样1,2前3阶频率统计表Tab.1 Statistical table of the first three order frequency of sample 1 and 2 Hz

对比表1中试样1、2可知，两组实验的黏合体为人工操作，故PZT的尺寸，织针与PZT黏合层的实际接触面积、厚度，黏合层内部的杂质浓度，织针与粘贴层的相对位置等均存在差异，进而导致两组实验的复阻抗、角度曲线以及各阶模态下的频率存在细微偏差。

3 ANSYS有限元仿真分析

采用ANSYS有限元仿真软件分析时，仿真对象的几何结构建模可以通过其内置的Design Modeler模块进行绘制，但用该模块绘制织针结构模型较为烦琐，故本文首先在SolidWorks软件中创建织针的三维几何模型，并将其转化为igs文件后导入ANSYS仿真软件中。完成导入后，在ANSYS仿真软件中对织针的材料属性进行设置，织针的材料为结构钢，定义弹性模量为2×1011Pa、泊松比为0.25、密度为7 850 kg/m3。材料属性定义设置后，完成织针的网格划分，并不设置织针任何约束条件，使织针处于完全自由状态下。在完成所有设置后，采用ANSYS仿真软件进行求解，织针1～3阶的模态分析结果如图8所示。前3阶段固有频率分别为383.1、896.7、1 019.0 Hz。将仿真结果与表1中实际测试值进行比较，比较结果如表2所示。

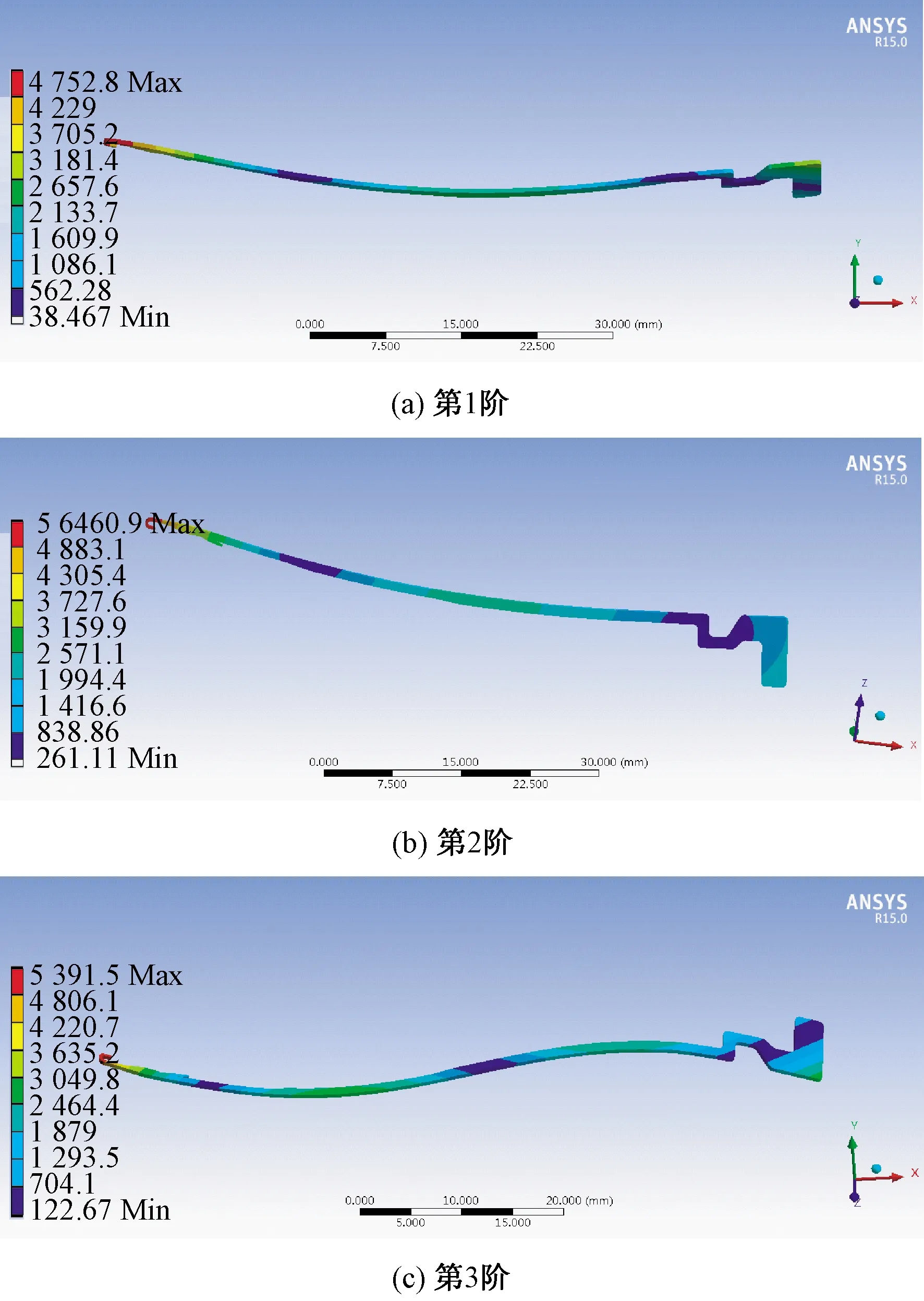
图8 织针前3阶模态分析结果图Fig.8 First 3 orders of modal analysis results of knitting needle. (a) Order 1; (b) Order 2; (c) Order 3

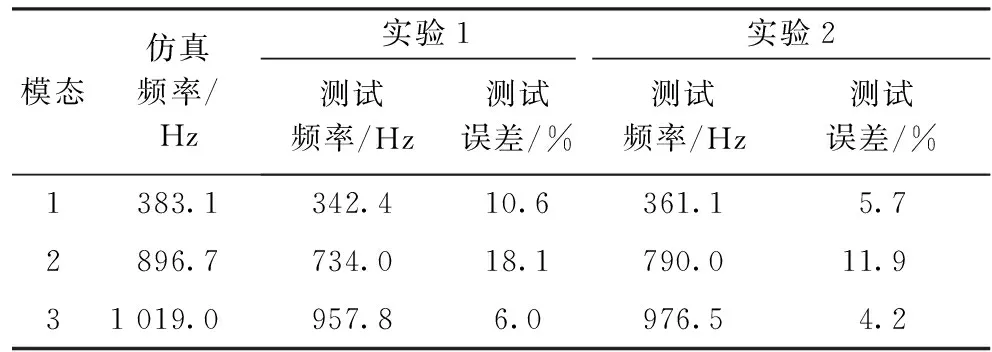
表2 织针仿真与测试结果误差结果汇总Tab.2 Summary of knitting needle simulation and test results error result

由表2所示数据可知，采用ANSYS仿真分析计算得出的固有频率值偏大。实验采用黏合体来代替织针进行固有频率的求解，额外引进的PZT、焊点、导线等物件增加了织针的质量，且对织针固有频率的测量产生了不可忽视的作用，织针固有频率与其质量的关系如式(3)所示：

(3)

式中，Δm为额外引进的物体导致的附加质量。

由式(3)可知，织针模态频率与质量的平方根成反比，通过在织针中部附加集中质量块Δm，改变了系统固有频率，且附加质量越大，织针模态频率越小。

为了更贴近实验中黏合体的实际结构模型，本文在原织针三维几何模型的基础上，加入PZT结构，形成黏合体几何模型，并对其进行ANSYS仿真分析，黏合体1～3阶的模态分析结果如图9所示。

图9示出黏合体做ANSYS仿真计算后第1～3阶的模态结果图，前3阶段固有频率分别为382.0、885.5、986.4 Hz。将仿真结果与表1中实际测试值进行比较，比较结果如表3所示。

相比于表2，其模态频率更接近实验值，证明了实验中额外引进的PZT等物质使得织针固有频率的测试值较仿真计算值要小。由表2、3所示数据可知，本文研究的纬编针织机织针自由状态下固有频率测试方法所得的第1阶，第3阶固有频率的测试值相对第2阶固有频率与计算值更为接近，这主要是PZT的额外引入，改变了织针的原有的质量与刚度，导致黏合体各阶的固有频率较织针各阶固有频率产生了偏差。另外，实验2的测试结果较实验1更接近计算值，这主要是两组实验的黏合体均为人工制造，黏合体的质量，刚度等参数均有细微偏差，故两组实验也存在一定的偏差。

本文研究的测试方法所得的固有频率值与织针计算值虽存在偏差，但偏差的范围是可接受的，特别是第1阶，第3阶固有频率的测试值，最小误差仅为4.2%。误差的引入主要是PZT的额外引入导致，选用尺寸更小但压电效应更强的PZT材料会减少测试数据与计算值的误差率。

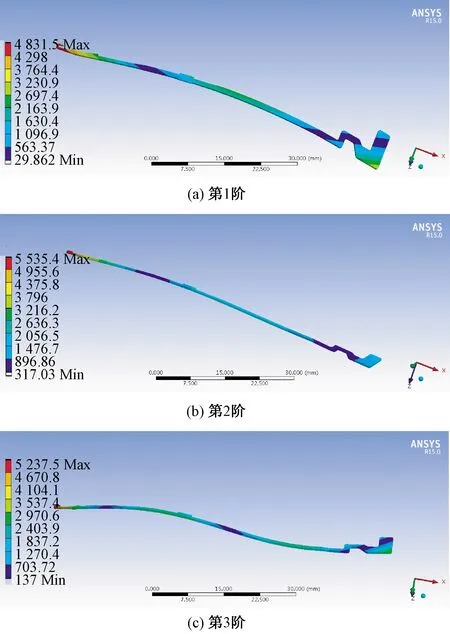
图9 黏合体前3阶模态分析结果图Fig.9 First 3 orders of modal analysis results of bonded body.(a) Level 1; (b) Level 2; (c) Level 3

4 结束语

纬编针织机编织过程中，织针是编织机构中重要的执行器件。织针编织过程中的振动特性直接影响织物的品质，而织针固有频率的有效测试是其振动特性研究的前提。本文针对纬编针织机织针结构尺寸微小、细长、横截面直径不定等特性，提出了一种黏合体结构，并采用阻抗分析仪对黏合体进行扫频测试，确定其固有频率，并以此测试频率近似估计织针的固有频率。通过2次实验的数据对比来验证本实验方法的可重复性，并对2组数据的不一致性进行了分析。

本文采用实验与仿真结合的方式，采用ANSYS软件对织针的固有频率进行计算，采用悬臂梁曲率、挠度理论对测振原理进行分析，从而验证实验的准确性。对比固有频率与实际计算值可知，虽存在PZT材料引入带来的误差，但本研究的测试方法总体实现了织针固有频率的有效测量。本文研究的针织固有频率的测试方法对织针固有频率的研究以及其他微小尺寸机构固有频率的测量具有一定借鉴意义。