初中数学辅助线添加技巧探究

郑爱萍

摘要：在初中数学几何问题解题过程中，辅助线发挥着桥梁作用。恰当的辅助线添加能够将复杂的几何问题简单化，所以掌握辅助线添加技巧十分关键。本文从辅助线的含义及作用着手，详细阐述了在初中数学学习过程中如何有效添加辅助线。

关键词：初中数学;辅助线;添加技巧

中图分类号：A 文献标识码：A

引言

在初中数学学习过程中，学生难免会遇到一些难以突破的几何问题。这时，添加辅助线无疑就成为数学几何难题解决的关键。不同的几何图形有着其自身独特的特点，辅助线可以将题目中的已知条件与隐藏条件加以串联，疏通解题者的思路。

一、辅助线的含义及作用

（一）辅助线的含义

辅助线是解决初中数学几何问题必不可少的解题手段，在初中阶段数学知识学习的过程中发挥着十分重要的作用。基于原图运用添加直线或者线段的方式，既可以将平面几何中相对分散的几何元素集中化，也可以使一些不规则的图形实现规则性转化。

（二）辅助线的作用

几何问题的解决是学生初中阶段遇到的一个全新的数学知识点，兼具多样性与严密逻辑性的几何知识在整个初中数学学习过程中占据着十分重要的地位。部分几何题的求解与证明，单纯依靠原图性进行分析和探究十分繁难，这就需要借助辅助线适当“补形”。原图基础上构建新的图形，为后续解题施以良好的铺垫。辅助线的添加并不会导致原有几何图形的性质发生改变，几何图形的形状及其与辅助线之间的边角关系均不会发生根本性的变化。并且添加辅助线之后，题目中一些隐藏的性质还会随之凸显，借助分隔或者延伸后得到的图形能够帮助学生快速找到问题解决的思路与方法，以便于高效解决初中数学中的几何问题。

二、初中数学辅助线添加技巧

（一）辅助线添加技巧

在几何问题解决过程中，图形不同、题目中呈现信息不同所画的辅助线类型也就不同，所以在解决几何问题时，需快速抓住题目中呈现或隐含的有效信息，并且掌握辅助线添加技巧。

1.仔细分析题目中隐含的信息

初中阶段，大多数几何问题题目中都隐含着一些条件信息，而准确把握这些信息也就成为解题的关键。但是由于所需证明的结论往往与题目中既定的条件之间缺乏清晰的逻辑关系，这时候就需要适当添加辅助线，为条件与结论之间架设“桥梁”，形成新的解题思路。在日常教学中，教师还需注重学生对几何题目中隐含信息敏感度的培养与提升，帮助学生在遇到几何问题时快速做出具有问题解决价值的辅助线。

2.以特殊点或线为问题解决的突破口

初中数学几何题目中通常会存在中点、角平分线或者三角形中线等一些特殊的点或者线段，在进行问题解决时可以以此作为突破口。解决问题时，首先需要学生熟练把握这些特殊点或线段的性质，由此着手进行辅助线的添加，帮助学生在建立逻辑关系的基础上有条理地分析复杂的几何图形，将繁难复杂的几何问题简单化。

3.从基本图形中发现辅助线

大多数人之所以觉得几何问题看上去十分困难，其实解题的关键就在于题目中那些被“故意省略”的条件，这时就需要借助辅助线化解难题。其实，在数学知识学习过程中所学的每一条几何定理都有与之相对应的基本几何图形。而添加辅助线的关键就在于学生一方面要对这些几何定理耳熟能详，另一方面还需要学生准确抓住这些基本图形，从中发现辅助线的身影。

（二）典型例题呈现--以等腰三角形为例

在初中数学几何问题中，等腰三角形是需要学生重点把握的特殊图形。等腰三角形本身具有诸多几何性质，它是轴对称图形，其顶角平分线与底边上的高及底边中线“三线合一”，并且等腰三角形的两底角大小相等。在进行关于三角形问题解决的几何题目中，就可以引导学生充分运用等腰三角形的几何性质为着眼点添加辅助线。

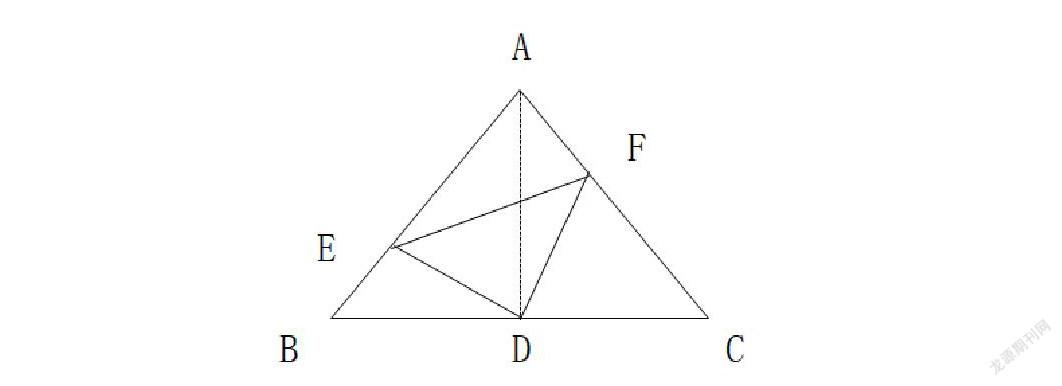
以下题为例：在△ABC中，∠A=90°，AB=AC，其中D点是BC边上的中点，点E和点F分别为三角形AB、AC边上的点，并且AF=BE。根据以上已知条件解决以下两个问题：（1）证明DE=DF;（2）证明DE⊥DF

分析：上述题目中，从题目给出的已知条件中分析可知，△ABC是一个等腰三角形，并且已知点D是该等腰三角形底边BC上的中点。依据等腰三角形“三线合一”的几何性质，可以将AD相连，绘制三角形底边中线，在借助相关数学定义加以反推，进而完成题目中所要证明的问题。

解：（1） ∵△ABC是等腰三角形，

∵ AB=AC ， D点为BC边中点，连接A点和D点得出線段AD

∵ 等腰三角形底边中线与底边上的高以及顶角平分线三线合一

∴ AD⊥BC，并且∠BAD=∠CAD

∵ ∠BAC=90°，

∴ ∠B=∠C=∠BAD=∠CAD=45°

∴ AD=BD

已知△AFD和△BED中，AF=BE，AD=BD，∠B=∠DAF

∴ △AFD ≌ △BED

∴ DE=DF

结语

总之，添加辅助线是学习数学几何知识的重要手段，它能够使原本不够清晰的解题思路变得更加直观明了。在初中数学几何知识教学过程中，教师首先需引导学生明确辅助线的含义及作用，在此基础上进一步引导学生熟练掌握辅助线添加的方法与技巧，从而利用新图形成功找出题目中几何图形之间的关系或隐藏的解题条件。

参考文献

[1]徐策. 平面几何常见添加辅助线的方法[J]. 中学教学参考，2020（2）：23-24.

[2]钟玉红.辅助线在初中几何解题中的应用[J].互动软件，2021（4）：2340.