基于扰动传播特征的随机Newell跟驰模型

张建波，朱远祺，孙建平

(1.北京交通发展研究院城市交通运行仿真与决策支持北京市重点实验室城市交通北京市国际科技合作基地，北京100073；2.深圳市城市交通规划设计研究中心股份有限公司，广东深圳518000)

0 引 言

机动车跟驰行为分析与建模是当前微观交通仿真的关键研究内容之一.一方面，跟驰行为随机特征是影响道路交通状态的重要因素，与交通状态演化规律密切相关.作为联系微观驾驶行为与宏观交通状态演化的关键参数，交通扰动传播特征在交通流陡降(Breakdown)、宽移动阻塞(Wide Moving Jam)和拥堵蔓延消散规律分析等方面均具有重要作用.但当前研究在跟驰行为随机特征(如车头时距的概率分布)，扰动传播速度和交通状态演化(如交通流陡降)三者间的量化联系方面仍比较匮乏.虽创造性地构建了车头时距与扰动传播特征的几何关系，但原始Newell 模型在刻画驾驶行为与扰动传播的随机特征关系方面能力明显不足.相关针对随机特征刻画能力的改进研究往往忽视车头时距与扰动传播速度的量化联系.另一方面，以北京为代表的国内城市道路交通具有典型的混合交通流特征，其驾驶行为易受各种因素影响.现有微观驾驶行为研究往往因为缺乏本地化的实测轨迹数据而产生模型参数不适用的问题，无法准确刻画国内道路环境下机动车驾驶行为特征[1].

近十余年，卫星定位技术、交通视频和驾驶模拟等数据采集方法不断完善，为微观驾驶行为研究带来了新机遇.美国联邦公路管理局开展了NGSIM(Next Generation Simulation)项目，通过在高空架设摄像机采集道路交通视频并提取车辆运行轨迹数据.Ossen 等[2]通过直升飞机从空中拍摄交通视频以获取机动车轨迹数据.以NGSIM 为代表的机动车轨迹数据不仅能反映运行车队中机动车的相互作用，还能体现真实交通环境对驾驶行为的影响，为机动车微观驾驶行为随机特征研究提供有力的数据支撑.Lochrane等[3]通过数据分析发现，不同的道路交通条件显著影响车头时距的分布特征.Wagner[4]利用多源数据分析了跟驰行为参数的随机特征，证明车头间距统计参数与速度的显著相关性.Ossen[5]将跟驰行为的随机性分为驾驶员外部异质性和内部随机性.Laval 等[6]将布朗运动引入跟驰模型刻画驾驶行为随机特征.

本文以北京市快速路为案例场景采集交通视频，并提取小汽车运行轨迹数据；以此为基础，分析本地化小汽车跟驰行为随机特征并建立概率分布模型；为改进原模型对驾驶行为与扰动传播随机关系的刻画能力，进一步提出基于扰动传播特征的随机Newell 跟驰模型，建立跟驰车头时距与扰动传播速度间的随机联系，以更好地支持交通状态演化规律(如交通流陡降、拥堵蔓延消散)的研究.

1 数据采集与处理

1.1 视频采集与轨迹提取

为获得反映本地化驾驶环境特征的机动车跟驰轨迹数据，本文通过拍摄交通视频提取车辆轨迹数据.视频采集自北京市四环快速路红领巾桥路段，在路侧高层建筑上架设高清摄像机拍摄得到工作日2 h交通流视频.视频主要包括快速路主路北向南4车道约300 m范围的交通流运行情况.如图1所示，单车道车辆速度时空图可以展现车队的运行特征及扰动传播过程(如图1(b)中箭头线所示).

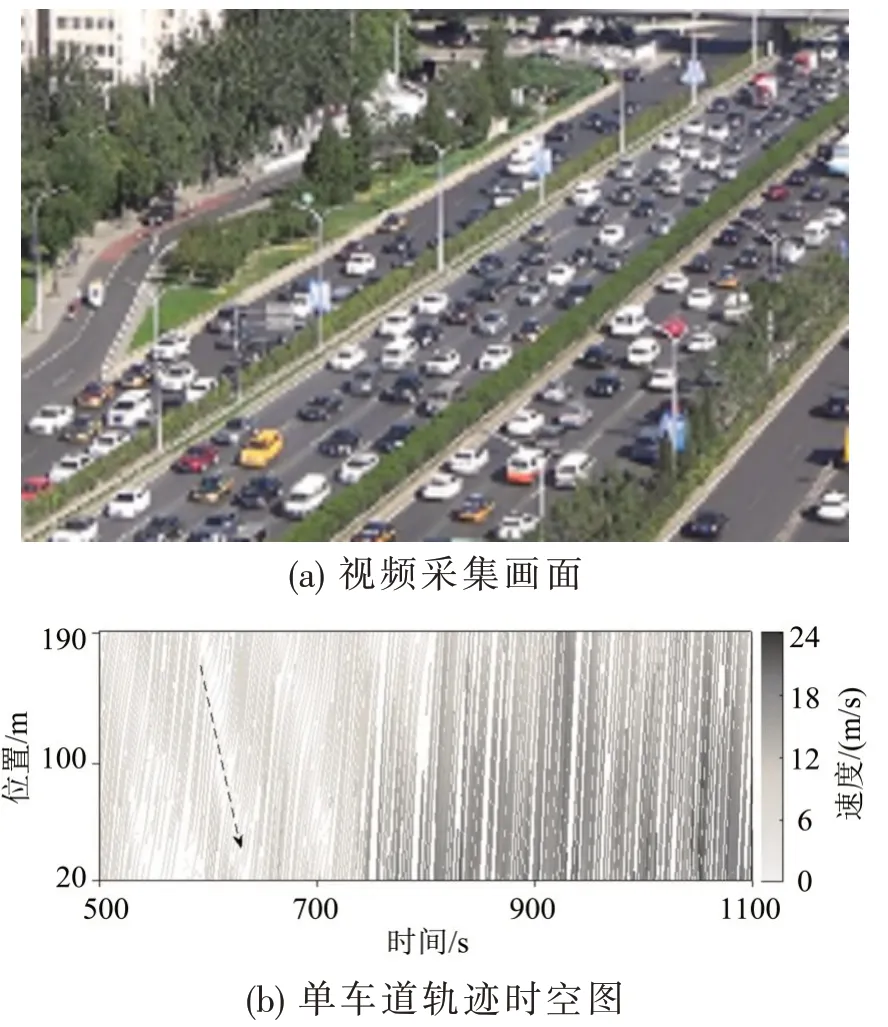
图1 视频采集与单车道的车辆轨迹时空图Fig.1 Video collection and spatial-temporal diagram of vehicle trajectories on single lane

车辆轨迹信息提取过程如下：首选，在视频中标注车辆信息，利用机器学习方法训练车辆识别模型，从而识别视频画面中的车辆；随后，以快速路为基准建立坐标系，依据实测距离建立不同位置像素的距离转换矩阵；最后，对视频逐帧处理以识别并追踪车辆的瞬时位置信息.如表1所示，最终获得近5 000 余辆机动车的原始车辆位置信息40余万条，时间粒度为0.2 s.通过差分方法获得车辆横向和纵向运动的瞬时速度和加速度等数据.

表1 车辆原始轨迹数据Table 1 Vehicle original trajectory data

1.2 轨迹数据质量控制

原始轨迹数据因存在随机噪声无法直接应用于驾驶行为的速度和加速度特征分析，需对原始数据进行清洗与滤波处理.本文以车队一致性和内部一致性约束为基本原则，先对少量数据极值进行差值替换；再采用对称指数平滑算法(Symmetric Exponential Moving Average Filter，SEMAF)[7]对轨迹数据进行滤波.对称指数平滑算法以指数作为平滑核的权重因子对轨迹序列进行平滑加权处理，以消除高解析度轨迹序列的扰动误差.

车辆n在ti时刻的位置数据点xn(ti) 位于平滑窗的中心，权重因子最大；其前后数据点的权重因子随离中心点的距离增大而逐渐减小.平滑后的坐标位置(ti)为

式中：i表示离散时间标记，i∈{1,2,…,NN} 为位置数据总条数；k为平滑窗内离散时间标记；Z为对称指数平滑的权重因子之和；T为平滑时长，即数据处理的时间长度，根据数据情况进行标定取值，本文经参数敏感性分析，确定横向和纵向位移的平滑时长T分别为1.2 s 和1.4 s；Δ为根据平滑时间长度和数据采集时间粒度计算得到的平滑核宽度，表示平滑和内的数据点范围；w为平滑窗宽度；Δt为轨迹提取的间隔时间.

如式(4)所示，设置平滑窗宽度w为平滑核宽度Δ的3倍，且平滑窗宽度在轨迹序列的前后边界逐渐缩短，以保证轨迹点数量不足的边界数据得到处理.

1.3 跟驰行为参数提取

通过轨迹数据筛选，提取有效小汽车跟驰行为数据约32 万条.从中提取跟驰行为的车头时距和反应时间等特征参数.

(1)车头间距/时距.

提取车头时距的同时，根据后车瞬时速度对车头时距进行分类，即

式中：dn(t)、hn(t)分别表示车辆n在时刻t与跟驰前车的瞬时车头间距(m)、车头时距(s)；yn(t)表示车辆n在时刻t的纵向位置(m)；vn(t)表示车辆n在时刻t的纵向速度(m/s)；v表示车辆瞬时速度(m/s)；round(⋅)函数表示四舍五入保留整数；V表示跟驰后车的瞬时速度区间.

(2)反应时间与扰动传播速度.

本文小汽车跟驰行为反应时间(Reaction Time)是指后车对前车扰动做出响应动作的延迟时间.相关研究普遍采用相关系数或回归分析从轨迹数据中提取跟驰行为反应时间.但其前提是假设个体车辆的反应时间为定值，不随交通状态或驾驶员状态变化.这与实际的跟驰行为特征存在差异.

本文采用文献[8]中动态时间规整算法(Dynamic Time Warping，DTW)从轨迹中提取小汽车跟驰行为的反应时间和扰动传播速度等特征参数.DTW算法是通过比较相似性将不同长度的两个时间序列进行匹配处理的一种时间序列匹配算法，该特点恰好符合反应时间动态变化的随机特征.设跟驰过程中前车速度、后车速度的时间序列分别为X={xm}、Y={yn}，其中，m=1,2,…,M，n=1,2,…,N分别表示前车、后车速度的离散时间编号(M和N分别表示前车、后车的轨迹数据条数).两车速度时间序列中任意两个时间点之间速度的费用函数为

则两个速度时间序列的累积费用函数表示为

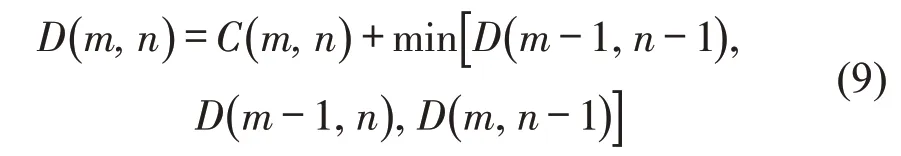
对应的感知反应时间τ和停车间距s可由匹配速度点的时间、纵向位置信息计算获得，即

式中：tn、tm分别为xn、xm的对应时间(s).

该方法可根据轨迹变化特征动态匹配前后车的“反应点”，跟驰轨迹匹配示意结果如图2所示.可以看到，后车对前车刺激的反应时间随前车速度变化显著变化.最后获得小汽车跟驰行为反应时间、停车间距与扰动传播速度等数据共4万余条.

图2 基于DTW 算法的轨迹匹配Fig.2 Trajectory matching based on DTW algorithm

2 跟驰行为随机特征分析

2.1 车头间距/时距

按式(7)以1 m/s为间隔划分速度区间，统计不同速度区间下跟驰行为车头间距特征.如图3(a)所示：随小汽车跟驰速度升高，车头间距平均值和标准差均逐渐增大；速度越高，跟驰中车头间距的波动性越大.图3(b)为部分速度区间下车头时距分布的拟合结果.分析结果表明，分速度区间的车头时距/间距分布可以用对数正态分布进行有效拟合，拟合参数如表2所示.

图3 不同速度区间下跟驰参数统计Fig.3 Statistics of car-following parameters under different speed intervals

2.2 反应时间与扰动传播速度

反应时间体现跟驰车辆对前车刺激的响应延迟，是影响驾驶行为特征和交通状态稳定的重要因素.图4中小汽车跟驰反应时间τ、扰动传播速度w和停车间距s均呈对数正态分布，其拟合结果为

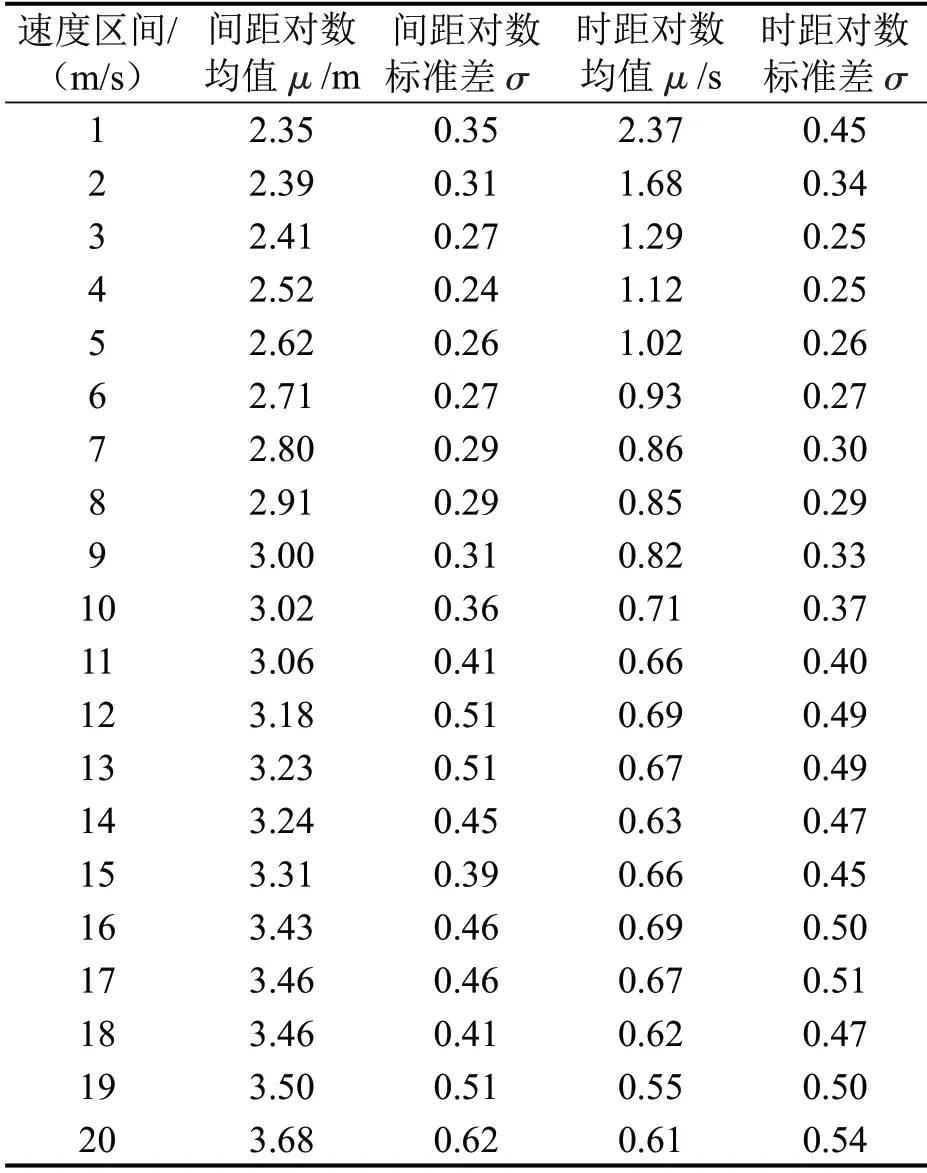
表2 不同速度区间下车头间距/时距的对数正态分布拟合参数Table 2 Fitting parameters of lognormal distribution of spacing/time headway under different speed intervals

图4 反应时间与扰动传播速度分布Fig.4 Distributions of reaction time and disturbance propagation speed

小汽车反应时间分布峰值与数学期望分别为1.0 s和1.57 s；扰动传播速度的分布峰值与数学期望分别为4.0 m/s和6.78 m/s；停车间距的分布峰值与数学期望分别为6.5 m和9.16 m.

3 基于扰动传播的随机Newell跟驰模型

构建基于扰动传播特征的随机Newell跟驰模型，并从交通扰动特征刻画与交通流参数特征等角度对模型效果进行分析.

3.1 改进的随机Newell跟驰模型

(1)Newell跟驰模型.

Newell 跟驰模型[9]因建立跟驰行为特征参数与扰动传播特征的量化联系，被广泛应用于驾驶行为和交通状态关系研究.Newell模型中车头间距为

式中：dn为车辆n与前车的车头间距(m)；vn为车辆n的速度(m/s)；τn为车辆n的反应时间(s)；sn为停车间距(m)；wn为扰动传播速度(m/s).

Newell跟驰模型假定车头间距d和车速v(不超过自由流速度vf)呈线性关系，如图5(a)所示.对于同一个后车，τ和d是固定常量.但数据表明，即使是同一驾驶员，其反应时间τ也是随时间不断动态变化的.如图5(b)所示，当前车发生时长为tr、速度为vr的扰动并恢复正常行驶后，会先后产生减速点D0和加速点A0，其扰动的减速和加速过程分别经历后车的减速反应时间τD和加速反应时间τA的延迟后向上游传播.反应时间的变化不仅影响跟驰车辆的车头时距变化，也影响扰动传播的速度特征.

(2)改进的随机Newell跟驰模型.

如图6所示，在前车扰动发生前、后速度v0、vr和后车到达时距h0确定的情况下，后车反应时间(τA和τB)越小，扰动的传播速度越快，对应速度变化后的车头时距(hA和hB)也越大.由几何关系可以推导反应时间τ和扰动发生前、后速度v0、vr，扰动发生前后车头时距h0、hr，及扰动传播速度w之间的量化关系为

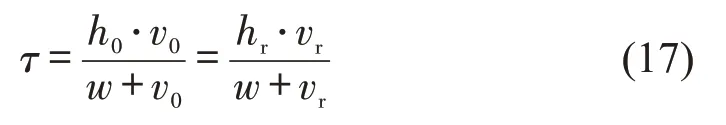
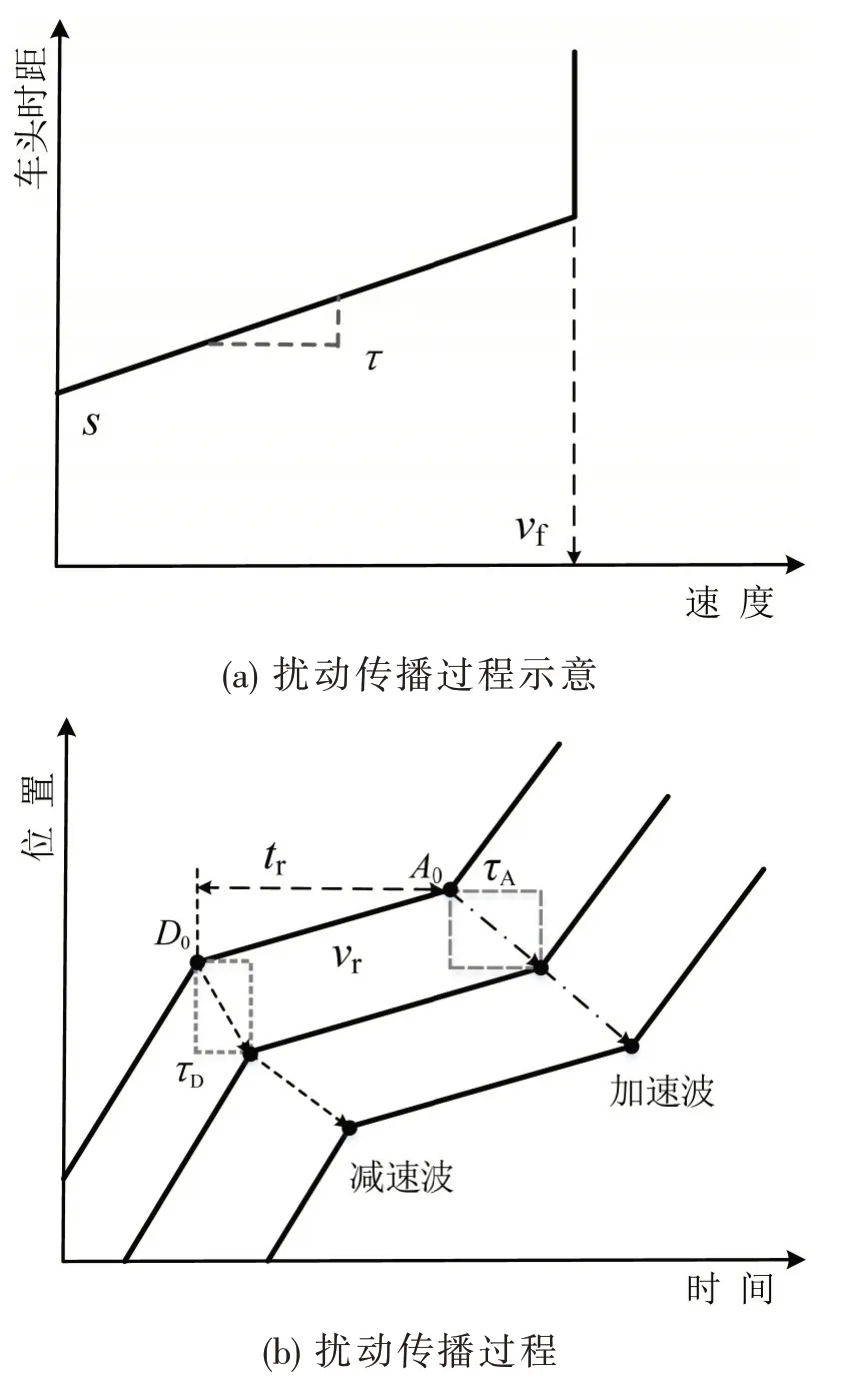
图5 Newell 跟驰模型与扰动传播过程Fig.5 Newell car-following model and disturbance propagation diagram

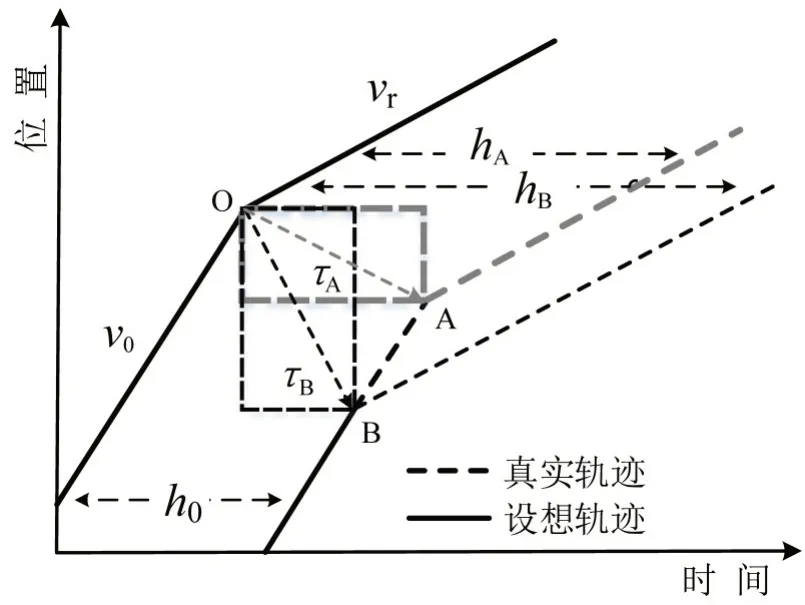
图6 反应时间、扰动传播速度和车头时距的关系Fig.6 Relationship among reaction time,disturbance propagation speed and time headway

基于上述关系，将式(17)和扰动传播速度随车速的变化特征引入Newell 跟驰模型框架中，得到能够刻画扰动随机特征的随机Newell 跟驰模型.此处省略时间参数t，新模型简写为

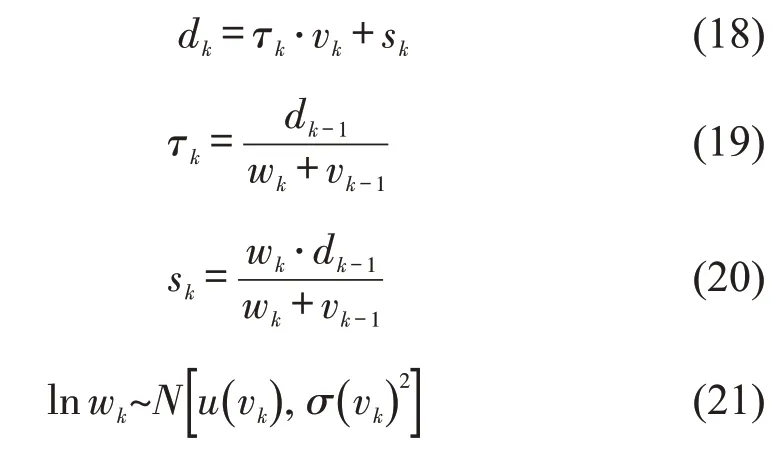
式中：dk、vk分别为跟驰车辆第k次速度扰动后的车头间距(m)、速度(m/s)；τk、sk、wk分别为跟驰车辆第k次扰动中的反应时间(s)、停车间距(m)、扰动传播速度(m/s)；dk-1、vk-1分别为跟驰车辆第k次速度扰动前的车头间距(m)、速度(m/s)；u(vk)、σ(vk)分别为速度vk下的交通扰动传播速度所服从的对数正态分布的均值、标准差参数.

针对自由驾驶阶段，假设驾驶员在自由行驶中所执行的自由流速度为vf，则改进Newell 跟驰模型的车辆位置为

式中：yn(t) 表示车辆n在时刻t的位置(m)；τk为车辆扰动的反应时间(s)；sk为车辆扰动的停车间距(m).式(22)第1 项为自由流状态的位置，第2 项为拥堵状态的车辆位置.

改进方法在保持反应时间、扰动传播速度与车头时距间量化关系的同时，保证反应时间τ始终大于0的同时小于速度扰动前后的车头时距，符合其物理约束.引入随车速变化的随机扰动传播速度w，不仅能更好地反映扰动与交通状态(速度)的联系；同时跟驰车辆的速度、反应时间和扰动后的车头时距的随机关系更为灵活.改进模型通过随机扰动传播速度量化确定了车头时距和反应时间的对应关系.

分速度区间标定扰动传播速度分布函数，结果如表3所示.如图7所示，在不同速度区间下扰动传播速度分布差异显著.速度区间越大，扰动传播速度的分布峰值越靠右，其期望均值和期望方差也更大.

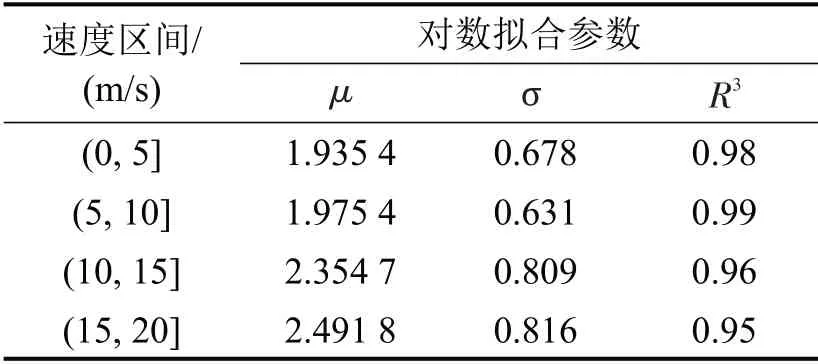
表3 随机Newell 模型参数标定结果Table 3 Parameters calibration results of stochastic Newell model

图7 分速度区间的扰动传播速度拟合Fig.7 Fitting curve of disturbance propagation speed under different speed intervals

3.2 模型效果验证与分析

针对改进Newell 模型，仿真分析改进模型在扰动传播特征刻画与交通流参数生成方面的效果.图8对比原始和改进Newell 跟驰模型对交通扰动的刻画效果.可以看出：改进模型更好地体现了交通震荡传播的随机性，扰动的加速波和减速波在向上游传播过程中表现出波动性，可以有效刻画扰动波的传播、放大与消散过程.

设计随机实验量化分析模型：以表2车头间距分布参数作为输入，均匀随机生成初始速度与扰动速度，应用改进Newell 模型生成速度扰动后的车头间距，并在相同速度区间下与实测车头间距分布情况进行对比，如图9所示.

由图9可知：在相同速度区间下，改进Newell跟驰模型生成的车头间距分布与实测轨迹获得的车头间距分布具有较高的一致性；实测车头间距分布相对更为离散，这是因为仿真未考虑换道等行为影响，仿真输出的车头时距相比实测的车头时距分布具有分布相对集中的趋势.统计发现，基于改进模型与实测数据获得的分速度区间车头间距分布的均方根误差(RMSE)在0.006～0.017之间，表明分速度区间的仿真与实测车头间距分布较为接近.

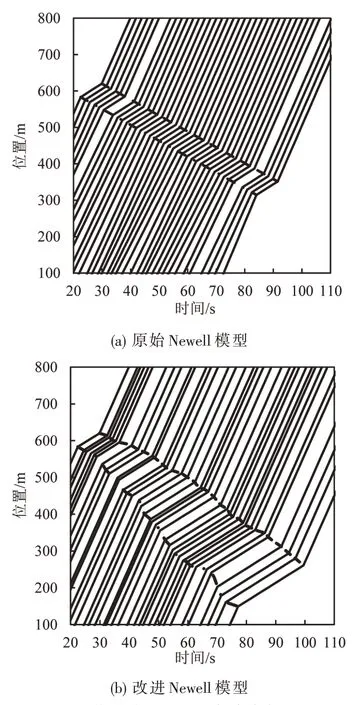
图8 扰动蔓延过程的仿真案例对比Fig.8 Simulation example comparison of a disturbance propagation process

以实测轨迹作为头车轨迹的输入参数，以改进Newell 模型仿真跟驰车队运行，生成流速密三参数关系如图10所示.改进Newell模型生成“倒三角”的密度—流量基本图.但仿真结果在反映拥堵的离散交通状态时存在一定不足.

图9 改进模型与实测数据车头间距分布对比Fig.9 Comparison of spacing headway distributions from improved model and measured data

图10 基于改进Newell 跟驰模型生成的交通流基本图Fig.10 Fundamental diagram of traffic flow generated by improved Newell model

4 结 论

本文提取北京快速路的车辆轨迹数据，应用DTW算法标定小汽车跟驰行为反应时间等特征参数；并建立考虑扰动传播特征的随机Newell 跟驰模型.基于DTW算法获得反应时间等跟驰特征参数具备随交通状态变化而变化的特性，更真实地反映了北京快速路的跟驰行为随机特征.改进的随机Newell跟驰模型建立以随机扰动传播速度为核心的车头时距与反应时间的定量关系，提高了Newell模型刻画微观驾驶行为与宏观交通状态演变之间关联关系的能力.

新模型能够更有效地支持交通流陡降、宽移动阻塞等交通演变现象的仿真再现，在微观交通仿真中具有丰富的应用场景.后续研究结合跟驰行为的不对称性特征，进一步完善模型对交通流松弛等现象的解释与再现能力.