城市区域物流无人机路径规划
张洪海,李 翰,刘 皞,许卫卫,邹依原
(南京航空航天大学民航学院,南京211106)
0 引 言
随着电商业务量的迅速增长,物流“末端一公里”配送面临的压力越来越大,无人机具有速度快、灵活性强的特点,无人机物流应运而生.在抗击新冠病毒疫情期间,武汉市运用物流无人机进行医疗物资配送,取得良好效果[1].可以预见,未来会有大量物流无人机在城市空域运行,因此,研究城市区域物流无人机路径规划方法具有现实意义.
目前,对物流无人机路径规划研究较少.文献[2]考虑无人机在人道救援方面的应用,提出在载荷和能耗约束下无人机运输成本最小的优化模型;文献[3]提出无人机运输整数线性规划模型并进行验证;文献[4]分析无人机物流运输过程的风险,设计配送系统进行仿真验证;文献[5]利用遗传算法和PSO算法,得出无人机在复杂环境的最优路径;文献[6]针对低空复杂环境,提出基于A*蚁群算法的路径规划方法并进行验证;文献[7]考虑低空空域环境和无人机运输任务等约束,建立多约束路径规划模型并进行验证.上述研究考虑的影响要素比较单一,缺乏在城市建筑物密集、规划空间复杂环境下进行路径规划的研究.
本文基于城市三维环境,考虑无人机性能条件,在满足无人机安全的前提下,构建航行总代价最小的无人机路径规划模型,设计基于栅格法的改进A*算法,以获得最佳配送路径.
1 问题建模
1.1 问题描述与假设
假设某城市区域存在物流需求点,位置已知,利用无人机从配送中心出发进行物流配送任务.无人机为可垂直起降的充电旋翼式无人机,存在性能限制,且在其出发后路径固定不变,不接受中途指派.为保证将货物安全快捷地配送到需求点,需要在飞行前进行路径规划.
1.2 环境建模
路径规划首先进行环境建模,采用栅格法表征飞行环境.设规划空间为OABC-O′A′B′C′的立方体区域,长、宽、高分别为Q、W、E,以O为原点建立3维直角坐标系.根据栅格大小lgrid,将规划空间划分为u×v×w个立体栅格,每个栅格的中心点作为待选路径点,其中,u=int(Q/lgrid),v=int(W/lgrid),w=int(E/lgrid),int()为取整函数.lgrid由地图分辨率和计算机性能决定.栅格法环境建模示意如图1所示,其中,灰色网格线将空域环境划分为一个个栅格,曲线表示在栅格中的飞行路径.
本文规划空间中所考虑障碍物为城市建筑物等静态障碍物,不考虑动态障碍物.传统赋值方法为0-1赋值法,即栅格存在障碍物赋值为1,否则为0,这种方法区分度小,容易丢失环境信息.本文运用[0,1]赋值法和栅格危险度[7]概念,赋值为1 的栅格不会被扩展为路径点,其他栅格可能被扩展但存在明显的危险度差异.栅格i的危险度di为

式中:Nobstacle(i)为栅格i周围障碍物数量;Nsurround(i)为栅格i周围栅格总数.

图1 栅格法环境建模示意Fig.1 Schematic diagram of grid environment modeling
1.3 路径规划模型
1.3.1 目标函数
设起始点S坐标为(x0,y0,z0),目标点G坐标为(xn,yn,zn),途经路径点Ci的坐标为(xi,yi,zi),其中i∈(1,2,…,n-1).考虑代价如下.
(1)航程代价.
定义无人机从S至G的航程代价为L,表达式为

(2)高度代价.
城市环境特点是建筑物高大且密集.定义无人机从S到G的高度代价为R,表达式为
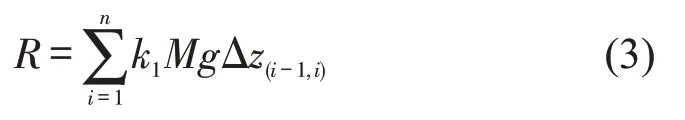
式中:k1为无人机高度变化惩罚系数;M为无人机总质量;g为重力加速度,取值为9.8 m/s2;Δz(i-1,i)为路径点Ci-1与Ci的高度差.
(3)危险度代价.
在城市进行物流配送必须考虑安全因素.定义无人机从S到G的危险度代价为D,表达式为

式中:k2为危险度惩罚系数.
综上,模型目标函数J为
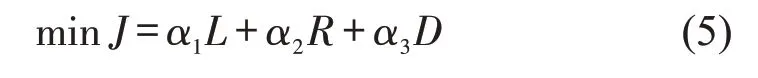
式中:α1、α2、α3分别为航程、高度和危险度代价的权重系数,满足:α1+α2+α3=1.
1.3.2 约束条件
(1)最小路径段长度.
相邻路径点距离不能小于最小路径段长度,约束为

式中:li为各路径段长度;lmin为最小路径段长度.无人机航程为各路径段长度之和.
(2)最大航程.
无人机配送距离必须小于其最大航程,约束为

式中:Lmax为无人机最大航程.
(3)转弯角和俯仰角.
无人机进行转弯或升降时,若zi-1=zi,无人机进行转弯操作,满足约束

式中:βmax为最大转弯角;βi为无人机在路径点Ci转弯角.
若zi-1≠zi,无人机进行升降操作,满足约束
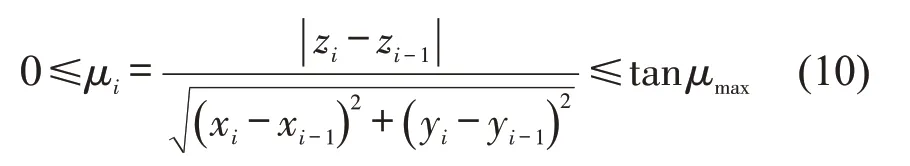
式中:μmax为最大俯仰角;μi为无人机在路径点Ci俯仰角.
(4)飞行高度.
无人机飞行高度的限制约束为

式中:Hmax、Hmin分别为最高、最低飞行高度,取决于无人机性能和空域政策.
(5)最大货物载重.
无人机载货上限约束为

式中:q为货物质量;qmax为最大载重;M′为无人机空重.
2 改进A*算法
2.1 传统A*算法原理
A*算法是常用的启发式算法,表达式为

式中:g(x)为起始点S至扩展路径点Cx的实际航程代价,称为实际代价函数;h(x)为扩展路径点Cx至目标点G的预估航程代价,称为启发函数.
2.2 改进A*算法设计方案
2.2.1 估价函数
(1)实际代价函数.
实际代价函数g(x)参照目标函数式(5),为

(2)启发函数.
合理的启发函数h(x)能有效提高搜索质量.传统启发函数采用单一航程计算方法,在有障碍物的环境中,采用欧氏距离作为启发函数会明显小于实际航程,而采用曼哈顿距离会明显大于实际航程,故本文采用欧氏距离和曼哈顿距离线性组合作为启发函数,表达式为

式中:ω1、ω2分别是欧氏距离、曼哈顿距离的权重系数,ω1+ω2=1.
2.2.2 双向搜索策略
为提高算法求解速度,本文采用双向搜索策略.设f1(x)=g1(x)+h1(x)和f2(x)=g2(x)+h2(x)分别为正向搜索和反向搜索的估价函数.首先,进行正向搜索,生成下一路径点后切换至反向搜索,反向搜索生成下一路径点后切换至正向搜索,如此交替进行.满足以下条件之一则停止搜索:①双向搜索在m点相遇,即在正向和反向搜索均搜索到某个路径点m,且被标记为代价值最小的路径点;②若双向搜索未能相遇,则对正向和反向搜索的2条路径进行比较,选取较短路径.
2.2.3 路径平滑处理
得到关键路径点组成的线段折角比较明显,需要进行平滑处理.本文采用B 样条法对初始路径进行优化,B 样条曲线具有曲率变化均匀的特点,能满足无人机飞行要求[8].
2.2.4 算法流程
算法流程如图2所示.具体步骤如下.
Step 1 获取起始点S和目标点G坐标,计算每个栅格的危险度.
Step 2 分别建立OPEN1、CLOSE1、OPEN2、CLOSE2列表,将S所在栅格加入OPEN1,将G所在栅格加入OPEN2.
Step 3 循环执行下述步骤.
Step 3.1 弹出OPEN1 和OPEN2 中代价值最小的正向路径点R和反向路径点T,把它们分别从OPEN1 和OPEN2 中删除,并分别放入CLOSE1和CLOSE2中.
Step 3.2 进行正向搜索,判断路径点R周围路径点R′.若为路径点G,则转向Step 4;否则,进行如下判断.
Step 3.2.1 若路径点R′在CLOSE2 中,说明双向搜索相遇,转向Step 4;否则,进入Step 3.3.2.
Step 3.2.2 计算f1(x),将拓展的子节点按顺序存入OPEN1.
Step 3.3 进行反向搜索,判断路径点T周围路径点T′.若为路径点S,则转向Step 5;否则,进行如下判断.
Step 3.3.1 若路径点T′在CLOSE1 中,说明双向搜索相遇,转向Step 5;否则,进入Step 3.3.2.
Step 3.3.2 计算f2(x),将拓展的子节点按顺序存入OPEN2.
Step 3.4 若OPEN1 或OPEN2 为空,则终止循环,进入Step 4;否则,返回Step 3.1.
Step 4 若为相遇,则从相遇点开始分别沿正向搜索和反向搜索的父节点上溯至各自起点,得到最优路径;若未相遇,则对搜索的路径进行比较,选取较短路径.
Step 5 采用B样条法对路径进行平滑处理得到最终路径,算法结束.
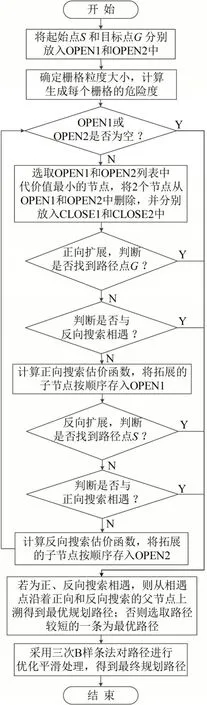
图2 算法流程Fig.2 Flow of algorithm
3 仿真与分析
3.1 仿真环境及参数设置
为验证方法的有效性,使用Visual Studio 和Matlab进行仿真实验.利用Google Earth获取香港太古城地理数据(地图分辨率为5 m).采用栅格法进行环境建模,作为无人机飞行环境.因缺乏实际案例数据,参照文献[7]设置参数值,如表1所示.
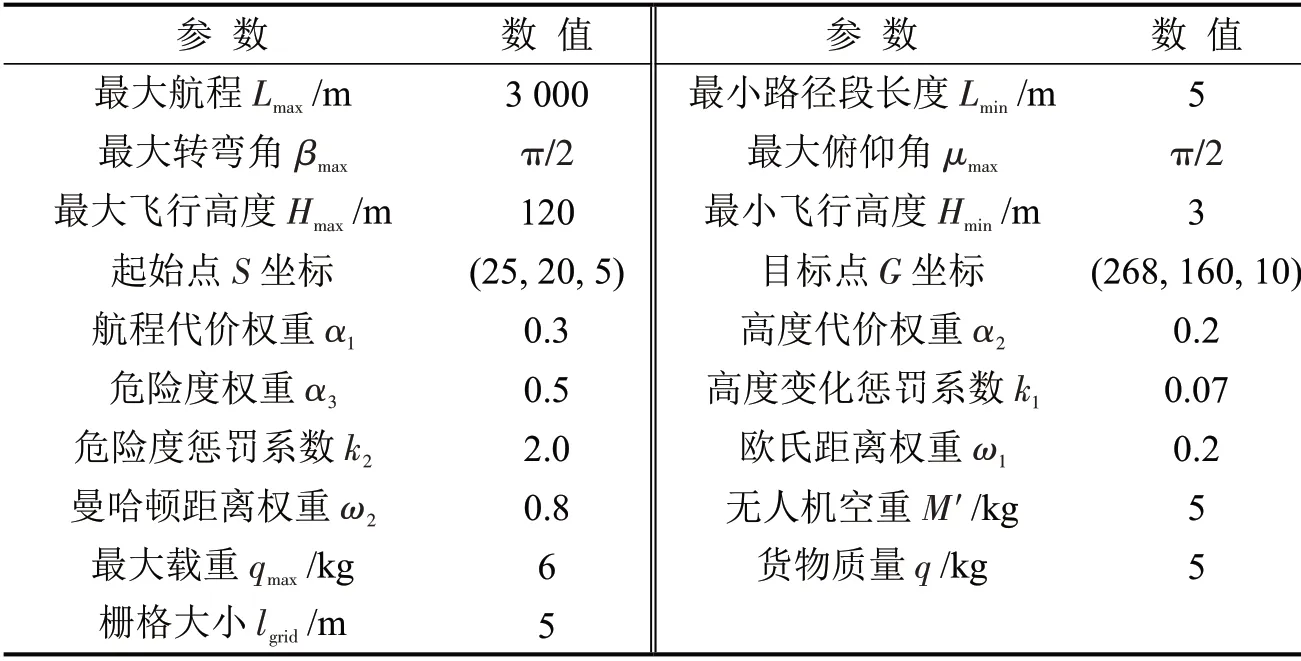
表1 参数设置Table 1 Parameter setting
3.2 仿真结果分析
仿真实验得到传统A*算法和改进A*算法路径规划,实验数据如表2所示,结果如图3所示.
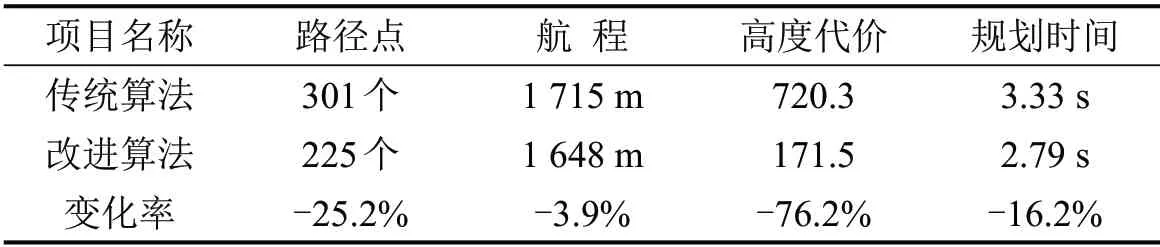
表2 传统和改进算法路径规划结果对比Table 2 Comparison of path planning results between traditional algorithm and improved algorithm

图3 物流无人机路径规划结果Fig.3 Results of logistics UAV's path planning
由表2和图3可知:2 种算法均能完成路径规划任务,改进算法的各项数据优于传统算法,尤其是高度代价比传统算法减少76.2%,优势显著.
为进一步分析算法性能,采用迪杰特斯拉算法进行路径规划,实验数据如表3所示,各算法规划结果如图4所示.
由表3可知,改进A*算法明显优于迪杰特斯拉算法,特别是高度代价和规划时间分别减少83.9%和98.7%.由图4可知,相较于其他算法,改进A*算法规划路径高度变化少,飞行稳定.因此,与传统A*算法和迪杰特斯拉算法相比,改进A*算法具有航程短,路径点少,高度变化少,求解速度快等优势,符合城市物流无人机飞行要求.

表3 迪杰特斯拉算法和改进A*算法路径规划结果对比Table 3 Comparison of path planning results between Dijkstra algorithm and improved A*algorithm
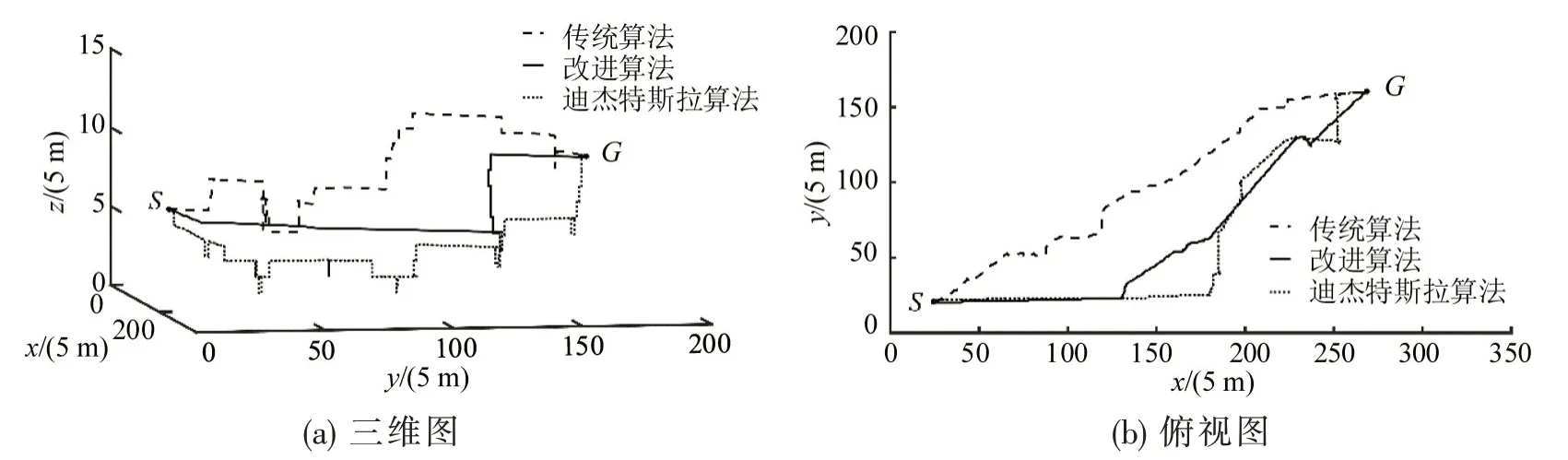
图4 不同算法路径规划对比Fig.4 Path planning results of each algorithm
3.3 参数设置分析
代价权重{α1,α2,α3} 和距离权重{ω1,ω2} 取值会对结果产生影响,故采用对照实验法对参数取值进行分析.
3.3.1 代价权重分析
城市物流配送首先要保证安全,因此,固定危险度权重α3=0.5 不变,分析α1、α2取值对结果的影响,进行21组对照实验.实验数据如表4所示.

表4 不同代价权重对规划结果的影响Table 4 Influence of different cost weight on path planning results
由表4可知,随着α1增大,航程呈现先增加后逐渐减少的趋势;高度代价前期比较稳定,从实验18 开始剧烈增加;危险度表现为先下降后稳定的趋势;规划时长在前8 组实验中波动较大,之后较为稳定.基于构建模型的目标函数并考虑算法时长,以实验17 所得结果为最佳,最优代价权重值为:α1=0.4,α2=0.1,α3=0.5.
3.3.2 距离权重分析
固定最优代价权重值不变,分析距离权重ω1、ω2的取值对结果的影响,进行21 组对照实验.实验数据如表5所示.

表5 不同距离权重对规划结果的影响Table 5 Influence of different distance weight on path planning results
由表5可知,随着ω1增大,航程为先减小后增大的趋势;高度代价和危险度先保持稳定后迅速增加;算法规划时长在波动中有增大趋势.基于构建模型的目标函数并考虑算法规划时长,以实验4所得结果为最佳规划路径,最优距离权重值为:ω1=0.15,ω2=0.85.
3.4 其他环境验证
为检验在其他环境下的性能,采用墨尔本地理数据进行仿真验证.起始点S坐标为(20,20,10),目标点G坐标为(230,230,8),其他参数保持不变,所得传统A*算法和改进A*算法路径规划,实验数据如表6所示,结果如图5所示.

表6 2 种算法路径规划结果对比Table 6 Comparison of path planning results of two algorithms

图5 其他环境下路径规划结果Fig.5 Path planning results in other environments
由表6和图5可知,在不同环境下本文算法依然有良好性能,除规划时间略长外,其他数据明显优于传统A*算法.而最佳参数需要根据规划要求,采用参数设置分析方法进行分析获得.
4 结 论
本文基于栅格法构建飞行环境,设计以航程、高度和危险度代价最小为目标函数的路径规划模型,有效实现多目标优化,贴合无人机在城市空域飞行实际.改进算法由欧氏距离和曼哈顿距离的线性组合作为启发函数,采用双向搜索策略搜索路径.仿真实验表明,改进算法较传统算法优势显著,说明改进算法具有合理性.本文方法可用于物流无人机路径规划,且规划结果受代价权重值、距离权重值影响.在不同环境和规划要求下,可采用本文参数设置分析方法得到最佳参数值.随着无人机技术的成熟,物流无人机在城市空域大规模运行为期不远,今后将会对多物流无人机协同路径规划开展研究.

