交叉口动态车道与交通信号协同优化方法

宋现敏，张亚南，马 林

(1.吉林大学交通学院，长春130022；2.中铁工程设计咨询集团有限公司郑州设计院，郑州450000)

0 引 言

城市道路网络交通需求波动导致交通拥堵日益频发，现有交通控制策略主要是信号配时优化控制冲突交通流的通行时间与通行顺序，在空间上无法应对交通流需求波动较大的情况.为提高信号交叉口时空资源利用率，研究人员开始关注车道分配的优化问题.Goldblatt[1-3]等为应对左转交通流造成的拥堵，提高左转车流通行效率，将左转车道和对向车道重新渠化，使左转车道在路段上通过连续流车道，穿过对向车道并进入对向车道外侧延伸出的新左转车道完成左转；Yiguang Xuan等[4-5]提出利用预信号引导转弯车辆提前进入交叉口等待区的组织形式，即阵列式交叉口(TI)，有效增加了各股车流释放效率；Wu Jiaming等[6]通过实验证明交叉口借道左转组织方式能够有效应对左转车流过大的情况.上述研究实现高峰时期交叉口空间资源的优化，但也存在应用上的不足，即重新渠化工程成本高，预信号设置导致额外延误，不能根据交通需求变化实时调整车道资源.因此，需要一种自适应的车道优化方法来应对交叉口不同流向交通需求分布不均衡的现象，故动态车道(Dynamic Lane Grouping，DLG)技术应运而生.周立平等[7]对可变导向车道长度和预信号配时进行研究，实验结果显示，可变导向车道的设置提高了交叉口的整体服务水平；李丽丽等[8-9]提出基于检测器数据的可变车道控制方法，通过实验证明可变导向车道功能和相位有效绿灯时间的最优组合能降低交叉口的车均延误和排队长度；Assi等[10]提出一种动态车道方案快速决策方法，降低了方案计算复杂度；曾滢等[11]构建车道功能与相位组合优化模型，并基于实际案例验证了模型的有效性；Alhajyaseen 等[12]建立交叉口车道优化与信号配时优化相结合的模型，通过仿真结果分析，该模型可以显著减少交叉口延误和排队长度.

以往车道功能优化大多在固定或预设的信号条件下进行，优化方案能够在一定程度提升交叉口空间利用率.但当交叉口整体交通需求增加时，只有充分利用交叉口的时间和空间资源才能有效提高交叉口的运行效率.因此，本文将研究动态车道和交通信号协同控制的优化效益情况；在此基础上，提出基于非线性整数规划的动态车道与交通信号协同优化模型；根据实时交通需求生成动态车道优化方案和信号配时方案，实现交叉口整体的时空资源优化.

1 动态车道与交通信号优化协同效益分析

动态车道的定义为交叉口进口道能够根据不同的交通需求动态地调整各进口道车道属性和分配方案.为验证动态车道与交通信号协同控制是否存在效益，在已有算法的基础上，对其进行效益分析.协同控制方案的步骤为：首先，确定进口道动态车道组合方案，以无掉头、信号控制采用左转保护相位的四车道进口道为例，单进口道的动态车道组合方案如图1所示；然后，基于实时检测的交通需求，以改进的韦伯斯特信号优化方法[13]生成交通信号配时方案；最后，以交叉口平均延误最小为目标选择最优动态车道组合方案和对应的信号优化方案.

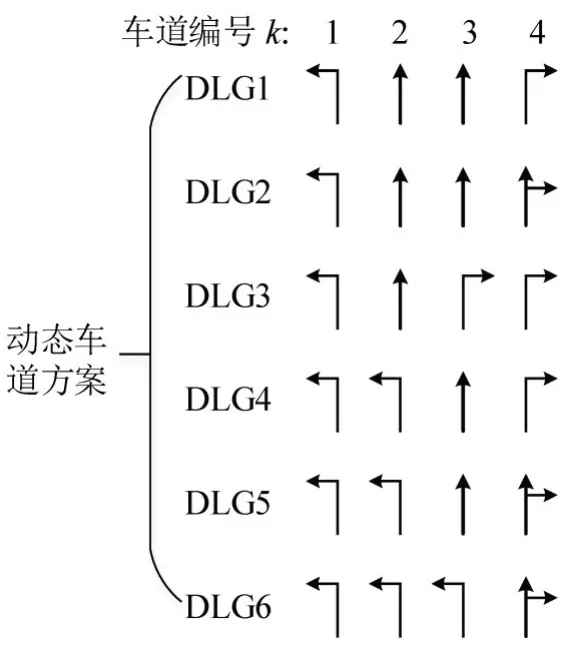
图1 动态车道组合方案Fig.1 Dynamic lane grouping scheme

本文以典型的十字交叉口作为研究对象，如图2所示，在初始信号控制条件下，车道属性固定设置为1 条左转车道，2 条直行车道和1 条右转车道的组合，4 个方向均为对称设置.信号控制方案中设置了保护相位配时方案.

图2 实验交叉口渠化及原始交通信号相位Fig.2 Intersection channelization and original traffic signal phase

为有效对比交通需求变化带来的效益差异，对初始交通需求条件进行限定，规定初始交叉口需求如表1所示.

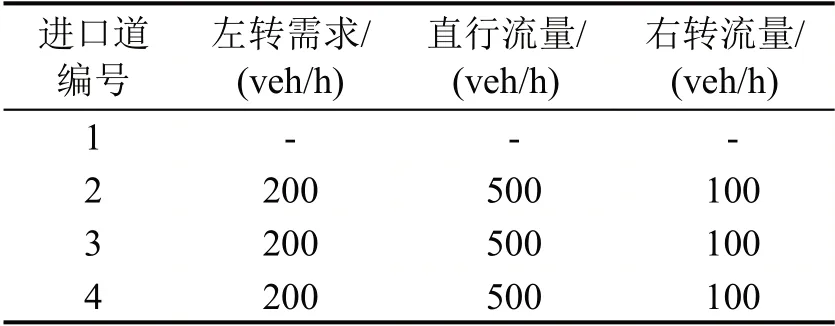
表1 各进口道转向交通需求Table 1 Traffic demand in different directions of each entrance

以进口道1的交通需求为变量，其他进口道交通需求为固定值.分析进口道1的总量交通需求波动和转向交通需求波动这两种场景下，协同优化控制方案与无车道优化的传统信号控制方案下交叉口的运行状况.

进口道的转向交通需求固定，总量交通需求变化时，两种方案的交叉口平均延误如图3所示，方案1 为无车道优化的传统信号控制方案，方案2 为动态车道与交通信号协同优化控制方案.图3(a)、(b)、(c)分别代表进口道1基准总量交通需求为600，1 200，1 400 veh/h，以及左转、直行、右转车辆比例为1∶2∶3 的情况.交通需求在基准值基础上变化代表其波动性，变化程度越大，其波动性也越大.在3 种基准总量交通需求下，方案1 的基准配时方案如图3(d)所示.由图3可知，总量交通需求波动越大，协同控制降低延误程度越明显.

当总量交通需求固定，转向交通需求变化时，两种控制方案的交叉口平均延误情况如图4所示，图4(a)、(b)、(c)分别代表进口道1 总量交通需求分别为400，800，1 200 veh/h 的情况，转向交通需求以基准需求为基础进行变化.由图4可知，转向交通需求波动越大，协同控制降低延误程度也越明显.

由效益分析可知，动态车道和交通信号协同控制无论在总量交通需求变化还是转向交通需求变化时，延误均处于最低值.

2 动态车道与交通信号协同优化模型

经验证，动态车道交通信号协同控制在交通需求越大，交通波动性越大或转向需求变化明显的情况下适用性越好.此外，应用方案交叉口的进口道车道数量至少有4条车道，与其上游交叉口保持足够距离，有信号机感应控制模块来实时获取交通需求数据.本文以单向四车道十字交叉口为研究对象，在不考虑直左右全混行车道，掉头交通流和行人与非机动车干扰的前提下，提出动态车道与交通信号协同优化控制模型.

图3 总量交通需求变化时控制方法效益对比Fig.3 Average intersection delay in four scenarios where traffic demand varies by total flow

图4 转向交通需求变化时控制方法效益对比Fig.4 Average intersection delay in four scenarios where traffic demand varies by turning proportion

2.1 参数说明

模型输入参数和变量如下：

i——交叉口方向序号，i=1,2,3,4 分别表示北、东、南、西方向；

ni——i方向进口道车道总数；

j——交通流转向编号，j=1,2,3 分别代表交通流左转、直行与右转；

k——车道编号，k=1,2,3,…,ni分别代表从路侧到路中的进口车道；

qi,k,j——i方向k车道j交通流转向的交通需求(veh/h)；

di,k——i方向k车道的控制延误(s)；

ci,k——i方向k车道的通行能力(veh/h)；

xi,k——i方向k车道的饱和度；

si,k——i方向k车道的饱和流量(veh/h)；

——i方向k车道上直行交通流的饱和流量(veh/h)；

ri,j,k——i方向k车道j流向交通流占比(当j=2 时，代表交通流为直行方向，此时ri,j,k=+∞)；

tp——稳定交通流的车头时距(s)；

tc——交通流从启动到稳定的时间(s)；

ts——清尾时间(s)；

T——分析持续时间(h)；

K——感应控制增量延误修正系数；

I——上游信号灯车辆换道、调节的增量延误修正系数.

δi——控制左转车道属性的变量，δi=1 表示i方向进口道的动态车道备选方案中使用单独左转车道，同时禁用直左混行车道，δi=0 时相反；

ψi——控制右转车道属性的变量，ψi=1 表示i方向进口道的动态车道备选方案中使用单独右转车道，同时禁用直右混行车道，ψi=0 时相反；

ni,LT/ni,LH/ni,TH/ni,RH/ni,RT——动态车道备选方案中i方向单独左转车道数量/直左混行车道数量/直行车道数量/直右混行车道数量/单独右转车道数量；

/——从i方向到达的左转交通流/右转交通流对应的驶离出口车道数量；

ηi,LT/ηi,LH/ηi,TH/ηi,RH/ηi,RT——动态车道优化方案中i方向单独左转车道数量/直左混行车道数量/直行车道数量/直右混行车道数量/单独右转车道数量；

gi,j——i方向j交通流的优化绿灯时间(s)，gi,j∈[gi,j,min,gi,j,max],gi,j,max与gi,j,min分别为方向i转向交通流j的最大和最小绿灯时间(s)；

Ls——交叉口总损失时间(s)；

C——优化周期时间(s)，C∈[Cmin,Cmax],Cmax为最大周期时间(s)，Cmin为最小周期时间(s)；

D——交叉口平均延误(s)；

λi,k——i方向k车道的绿信比(s)，是绿灯显示时间和信号周期的比值.

2.2 约束条件

动态车道与交通信号协同优化模型分为两部分：第1部分根据车道平衡输出可行的动态车道备选方案，并作为第2 部分的输入参数；第2 部分根据实时交通需求生成动态车道优化方案及信号优化方案.

(1)第1部分动态车道备选方案生成.

进口道车道总数ni应满足同时允许左转、直行及右转交通流占有车道，即

左转交通流占用进口车道数量必须大于等于驶离方向出口道的数量，即

其中，左转交通流驶离方向出口道必须满足

右转交通流占用进口车道数量必须大于等于驶离方向出口道数量，即

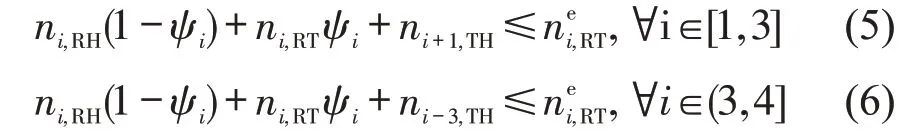
其中，右转交通流驶离方向出口道必须满足

动态车道的备选方案必须允许左转、直行及右转车流均占有行驶空间，故各方向车道需满足

对向左转信号相位(包括保护左转相位与许可左转相位)必须保持一致，故δi应满足

直左混行车道最多允许设置1条，右转混行车道同理，即

此外，车道数必须为非负整数，即

模型中变量的整数约束为

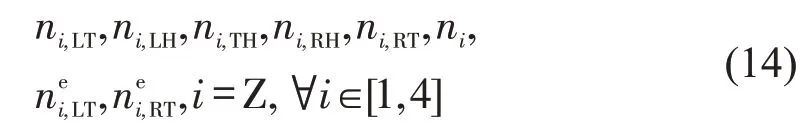
第1 部分模型的输出变量为：∀ni,LT,ni,LH,ni,TH,ni,RH,ni,RT,∀i∈[1,4].

(2)第2部分动态车道优化方案生成.

根据第1 部分输出数据，令∀ni,LT=Φi,LT，∀i∈[1,4]，∀ni,LH=Φi,LH，∀i∈[1,4]和 ∀ni,TH=Φi,TH，∀i∈[1,4].模型第2 部分的关键输入变量为交通需求矩阵，在信号配时中，各相位绿灯时间应满足对应的交通需求∀ni,LH=Φi,LH.

左转交通流占用车道应满足

直行交通流占用车道应满足

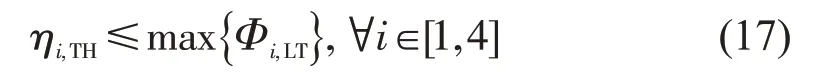
各转向优化车道数应为

对向相同相位的绿灯时间应保持一致，即

左转相位约束与第1部分一致，记为

各相位绿灯时间与周期的关系为

模型中变量的整数约束为

2.3 目标函数

在单车道延误模型基础上，以交叉口各进口道交通量及进口道转向交通流差异的交叉口平均延误为优化目标.其中，单车道控制延误公式为

动态车道与交通信号协同优化模型的目标函数为

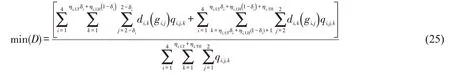
3 模型验证

3.1 方案切换条件

为保证交通流运行连续性，减少频繁切换方案造成额外延误，设置方案最小运行时间.在方案运行时间大于最小运行时间后，对方案进行效益判定.效益评价指标取交叉口平均延误的倒数，只有当新方案比原方案具有明显优势方可进行方案切换.协同优化方案切换判定流程如图5所示.

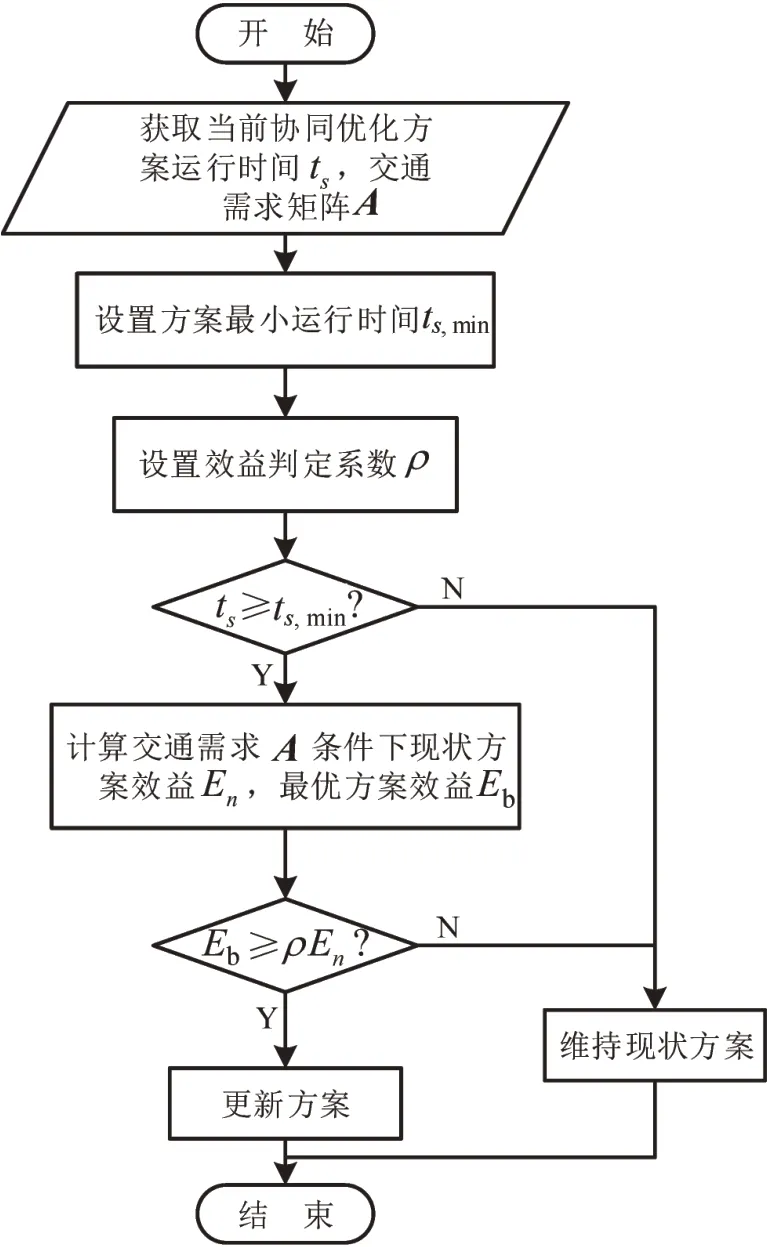
图5 协同优化方案切换判断流程Fig.5 Update flow of optimization method

3.2 模型求解和参数选择

模型为整数非线性规划，采用枚举法求解全局最优解.输入变量设置为：ni=4，δi=1，ψi=1或ψi=1,∀i∈[1,4]，各修正参数取I=1，K=0.5，T=0.25，ρ=1.1.

3.3 结果分析

(1)左转重交通流.

在左转重交通流下，交通需求及模型求解结果如表2所示.

由表2可知，在左转重交通流情况下，动态车道优化结果为该方向提供了更多左转车道，以适应交通需求的变化.

左转重交通流情况下动态车道对交叉口平均延误影响如图6所示.在单向左转、对称左转、相邻左转重交通流情况下，应用动态车道的交叉口平均延误均明显低于无动态车道的情况，分别降低了38.7%、50.1%和46.1%.此外，左转交通状况越复杂(左转、对称、相邻左转的交通状况复杂度依次增大)，协同优化的优化程度越明显.

(2)右转重交通流.

右转重交通流条件下动态车道方案如表2所示，右转重交通流实验采用右转车辆比例明显较高的情况.

由表3可知，在右转车辆比例较高情况下，动态车道优化方案为右转交通流分配多条右转车道.右转重交通流情况下动态车道对交叉口平均延误影响如图6所示，可知，应用动态车道的交叉口平均延误低于无动态车道的情况.在实际场景中，右转交通流往往波动较少，故该协同优化方法对右转交通流延误改善不大.

表2 左转重交通流场景下的动态车道优化方案Table 2 Solution of proposed model in case of heavy left-turn traffic flow

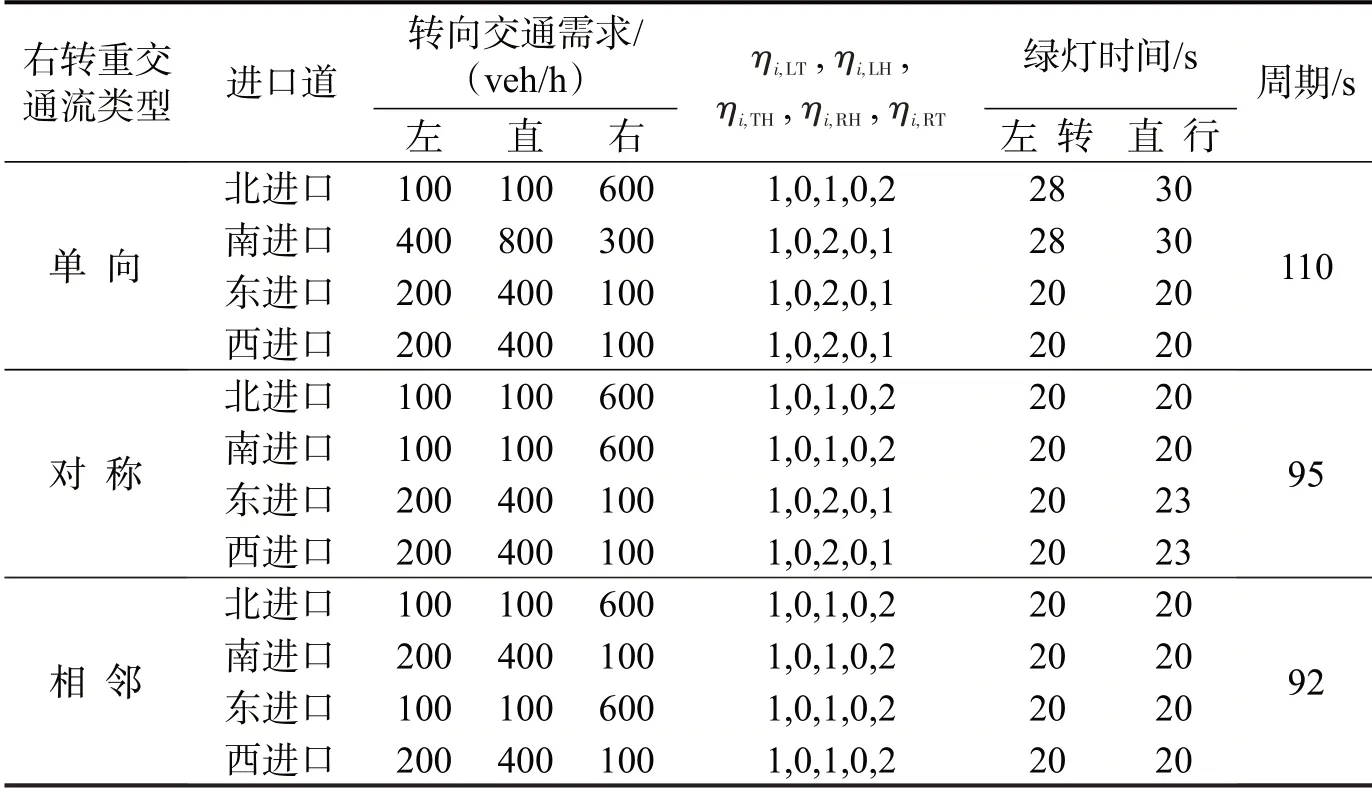
表3 右转重交通流场景下的动态车道优化方案Table 3 Solution of proposed model in case of heavy right-turn traffic flow

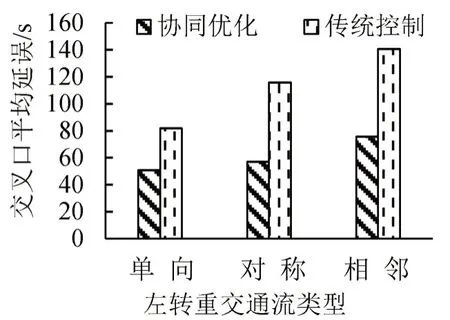
图6 左转重交通流情况下协同优化与传统方法延误对比Fig.6 Average intersection delay of optimization method and average intersection delay of traditional method in left-turn heavy traffic flow

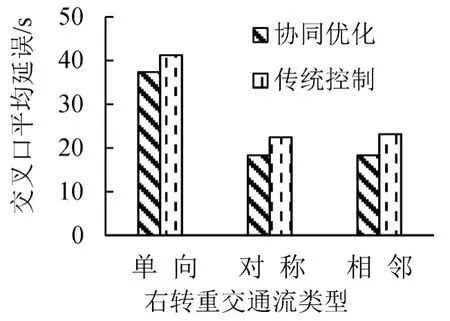
图7 右转重交通流情况下协同优化方法与传统方法延误对比Fig.7 Average intersection delay of optimization method and average intersection delay of traditional method in right-turn heavy traffic flow

4 结 论

本文构建基于非线性整数规划的动态车道与交通信号协同优化模型，模型求解方法简单可行，经实例验证，本文提出的优化方法动态车道与交通信号协同优化方法为重交通流方向提供了更多车道，且交叉口转向交通状况越复杂，协同优化效果越好.可以有效提高交叉口时空资源利用率，增加交叉口应对复杂交通需求条件的能力，为其在工程实践层面的应用提供了理论参考.未来可以进一步实现干线条件的动态车道时空资源优化方法.