再生混凝土梁抗剪承载力的可靠指标分析
陈秋宜,孙 畅,刘卫东
(上海理工大学 环境与建筑学院, 上海 200093)
再生混凝土作为一种绿色建材,主要是利用再生骨料部分或全部替代天然骨料配置而成的新型混凝土[1]。其中再生骨料是指由废弃混凝土经破碎加工而成的粒径小于40 mm的骨料。大量学者对再生混凝土材料性能以及再生混凝土结构性能进行了研究,包括再生混凝土梁、柱的承载力、抗震性能等[2-5]。相较于天然骨料,再生骨料的来源差异性较大,表面附着旧水泥浆体,生产过程中产生的损伤使其内部构造力差[6-7],故制成的再生混凝土呈现较大的离散性,导致各试验结论有很大的偏差。再生混凝土材料性能的差异性以及强度的离散性的增加在结构层面上会影响结构构件的安全可靠性,故再生混凝土结构的可靠指标能否满足《建筑结构可靠度设计统一标准》[8](GB 50068—2018)的要求需要进一步研究,这对于推广再生混凝土材料的使用是十分必要的。
对于再生混凝土构件的安全性可靠度评估上的研究,肖建庄等[9]分析再生混凝土梁受弯时在强度均值、标准值和设计值分别于普通混凝土相同的三种情况下再生混凝土材料分项系数的取值,并给出了建议数值。马辉等[10]利用蒙特卡罗法计算型钢再生混凝土柱的抗剪承载力计算公式的可靠指标,并给出了计算公式修正系数。但是由于试验中的构件数量有限,在再生混凝土的结构构件可靠性评估上各设计因素仍不够全面。为探究《混凝土结构设计规范》[11](GB 50010—2010)(以下简称《规范》)中抗剪承载力公式对于再生混凝土梁的适用性及可靠性,本文收集整理国内外大量再生混凝土梁的受剪试验数据,分析得到计算模式不定性系数,并采用验算点法进行可靠度分析,研究再生粗骨料取代率、剪跨比、配箍率等因素对再生混凝土梁抗剪承载力的影响,以期为再生混凝土梁的工程应用提供一定的参考。
1 再生混凝土梁抗剪承载力计算公式及不定性系数选用
1.1 再生混凝土梁抗剪承载力计算公式
对于梁的剪切破坏形态,再生混凝土梁与普通混凝土梁基本一致。由于工程中的梁基本上都配有箍筋,故本文主要研究再生混凝土有腹筋梁的抗剪承载力。韩定杰[12]、Li等[13]和Yanweerasak等[14]对不同再生骨料掺入量的再生混凝土梁进行加载试验,结果表明再生混凝土梁破坏模式主要表现为典型的剪压破坏形态,破坏时箍筋应变均达到钢筋屈服应变,且不随再生骨料掺入量改变。再生混凝土梁的抗剪承载力主要影响因素有再生粗骨料取代率、剪跨比、配箍率及混凝土强度等。Al-Zahraa等[15]、陈宗平等[16]和Liu等[17]研究结果表明再生骨料取代率对于梁抗剪承载力的影响相较于剪跨比、配箍率来说较小,抗剪承载力只是略有降低,降幅约控制在10%以内,同时廖一[18]发现再生粗骨料取代率在50%时抗剪承载力表现较好,最为接近普通混凝土。Rahal等[19]、Li等[20]、王亚梅[21]、Ignjatovic等[22]和杨卫闯[23]通过设计配合比研究再生混凝土有腹筋梁抗剪承载力的影响因素,其变化规律与普通混凝土梁一致,均随配箍率及混凝土强度的增大而增加,随剪跨比的增大而减小。
通过以往学者的研究,再生混凝土梁的剪切破坏形态及抗剪承载力的影响因素均与普通混凝土梁相近,故采用规范[11]中抗剪承载力计算公式分析再生混凝土梁可靠指标是可行的。规范[11]中混凝土有腹筋梁的抗剪承载力公式定义如下:
(1)
其中,对于再生混凝土的抗拉强度与立方体抗压强度之间换算关系选取肖建庄[24]提出的公式(2),考虑了再生粗骨料取代率对其抗拉强度的影响。
ft=(ar+0.24)fcu(2/3)
(2)
式中:λ为梁的剪跨比;ft为混凝土轴心抗拉强度;b、h0为梁的宽度和有效高度;fyv为箍筋强度设计值;Asv为箍筋截面面积;s为箍筋间距;ft为混凝土轴心抗拉强度;r为再生粗骨料取代率;fcu为混凝土立方体抗压强度;a值通过实验数据统计回归求得,a=-0.06。
1.2 计算模式不定性系数的确定
由于在进行再生混凝土梁抗剪承载力计算时所采用的基本假设与计算公式存在一定的误差,为讨论所用抗剪承载力计算公式的适用性,根据可靠度标准的规定,计算模式不定性系数需通过由计算模型得出的结果与由实际观测或者精确方法得出的结果进行比较,从而统计分析确定,用Xp表示。表1给出了五组二十二根再生混凝土梁的抗剪承载力的试验值与按式(1)、式(2)计算的计算值比值的结果,同时为了便于与再生混凝土梁的抗剪承载力进行比较,选取5根普通混凝土梁的抗剪承载力结果见表2。
根据表1和表2的试验值与计算值的比值,即可得出计算模式不确定性系数,将所得不确定性系数转换成图1和图2,以便直观分析再生混凝土梁与基准混凝土梁的Xp分布。从图1和图2中可以看出再生混凝土有腹筋梁及基准混凝土有腹筋梁的Xp均相对离散性较小,再生混凝土梁试验值与计算值的比值计算结果分布比较集中,其均值为1.411 838,标准差为0.173 865,普通混凝土梁虽然样本稍少,但得出的结果分布也较为集中,其均值为1.406 24,标准差为0.157 846。
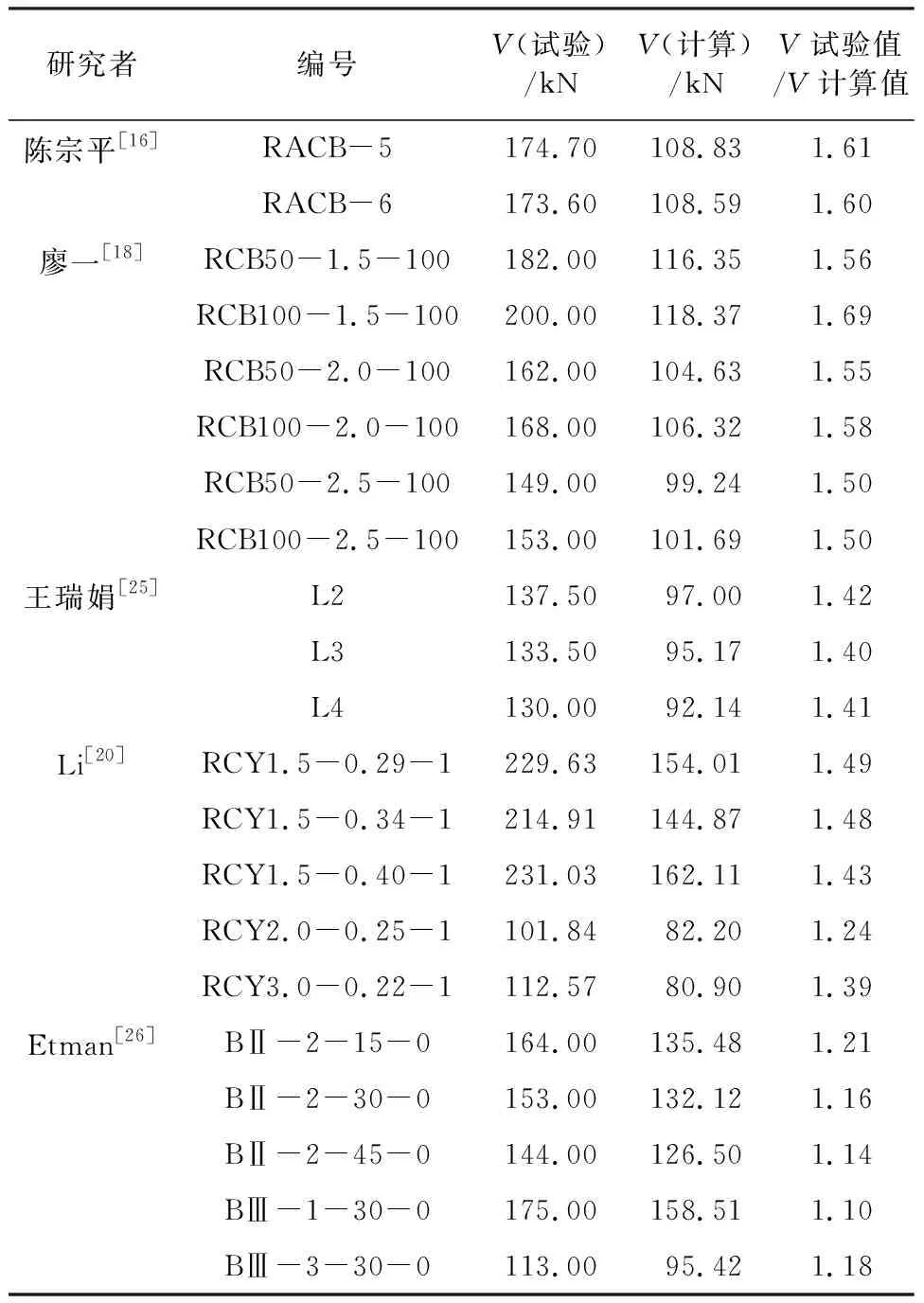
表1 再生混凝土梁抗剪承载力计算值与试验值的比较
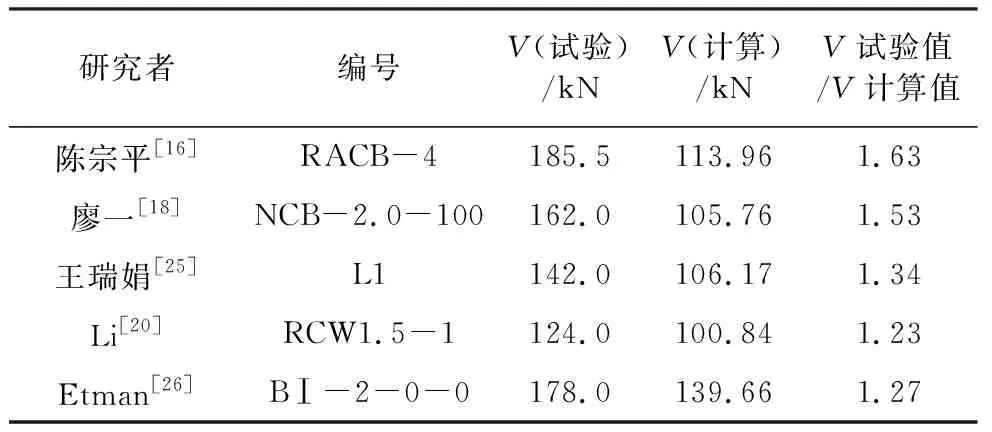
表2 基准有腹筋梁抗剪承载力计算值与试验值的比较
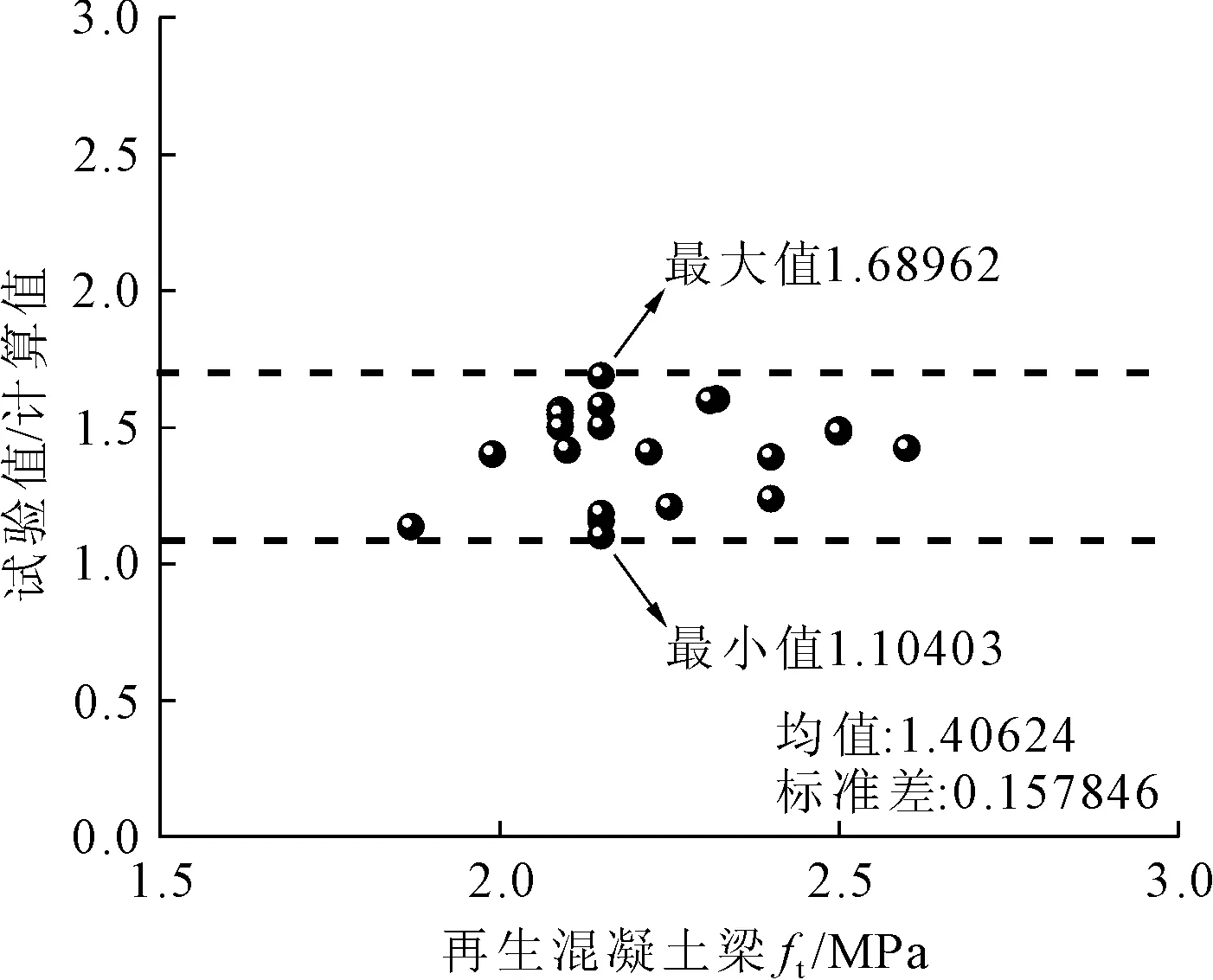
图1 再生混凝土有腹筋梁Xp分布
再生混凝土有腹筋梁与基准混凝土梁Xp的平均值与标准差对比如图3所示。从图中数据可看出,再生混凝土和基准混凝土梁的试验值均是大于计算值的,故根据规范[11]公式得出的再生混凝土和基准混凝土有腹筋梁都是安全的。再生混凝土梁Xp的均值小于基准混凝土梁,标准差大于基本混凝土梁,由于相差较小可忽略。
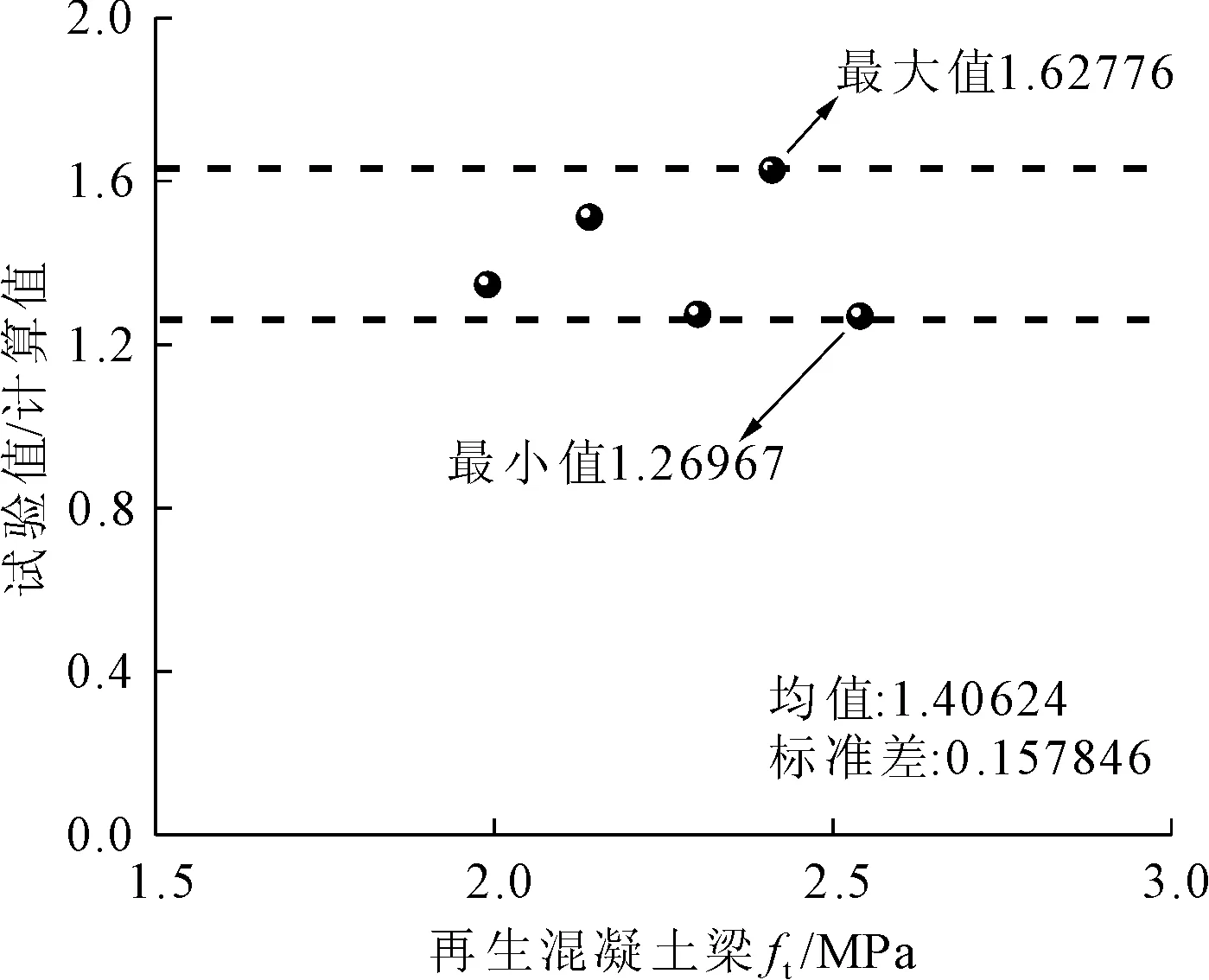
图2 基准混凝土有腹筋梁Xp分布
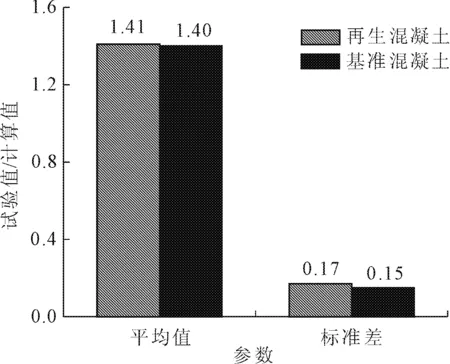
图3 再生混凝土有腹筋梁与基准混凝土有腹筋梁Xp的比较
由图3可以看出,再生混凝土有腹筋梁的计算模式不定性系数值与《再生混凝土》[24]书中的值相比偏小,这可能是由于所选取的试验数据中的ft和λ的取值比较集中,所以离散性较小。结合《再生混凝土》[24]一书,并由表1、表2可确定再生混凝土有腹筋梁抗剪承载力公式不定性系数的均值和标准差为1.41和0.17。基准混凝土有腹筋梁的抗剪承载力公式不定性系数的均值和标准差取为1.40和0.15。
2 再生混凝土梁抗剪承载力可靠指标计算理论及方法
2.1 功能函数的建立
对应于任意配筋率,梁的功能函数为:
Z=VR(fc,fy)-VS(G,Q)
(3)
式中:VR为截面抗力;VS为荷载效应。
对于截面抗力VR的计算,根据本文所选参考试验情况,所有梁均受集中荷载作用,先将规范[11]中有腹筋梁抗剪承载力公式即公式(1)进行转换后,转换后的公式如下:
(4)
式中:ρsv为配箍率。
考虑到由于抗力计算公式不精确引起的变异性,采用上节计算得到的计算模式不定性系数Xp,故再生混凝土梁的受剪抗力可表示为:
(5)
在结构分析时,只考虑荷载最大值,对于荷载效应VS,肖建庄[24]考虑了三种荷载类型的基本组合,分别是100%永久荷载、100%持久性楼面活荷载以及永久荷载与持久性楼面活荷载比例为1∶1情况下普通混凝土梁的抗剪可靠指标随配筋率的变化规律,结论表明在100%永久荷载下,梁的可靠指标最小,故本文仅考虑永久荷载作用下再生混凝土有腹筋梁的可靠指标。根据《建筑结构荷载规范》[27](GB 50009—2012),永久荷载G的均值系数为1.060,变异系数为0.070,服从正态分布。
基于极限状态设计时,首先根据荷载类型和截面承载力计算截面的抗剪承载力设计值VS,d,计算公式采用规范[11]中有腹筋梁抗剪承载力计算公式即式(4)。在100%永久荷载作用下,荷载效应VS,G的分布为:
(6)
VS,G的均值和标准差分别为:
(7)
(8)
式中:γG表示永久作用的分项系数,取γG=1.35。
此时再生混凝土梁抗剪的功能函数表达为:
(9)
2.2 再生混凝土梁抗剪承载力可靠指标参数统计
再生混凝土梁抗剪承载力可靠指标参数统计通常考虑梁的基本参数和抗力参数分布以及荷载效应的统计值。梁的截面尺寸选择与所收集试验数据中大多数梁一致,统一采用b=150,h=300。选用混凝土强度等级为C30, 纵筋使用HRB335热轧带肋钢筋,箍筋使用HPB235热轧光圆钢筋,其统计参数见表3。混凝土的强度假定服从正态分布,钢筋强度假定服从对数正态分布。
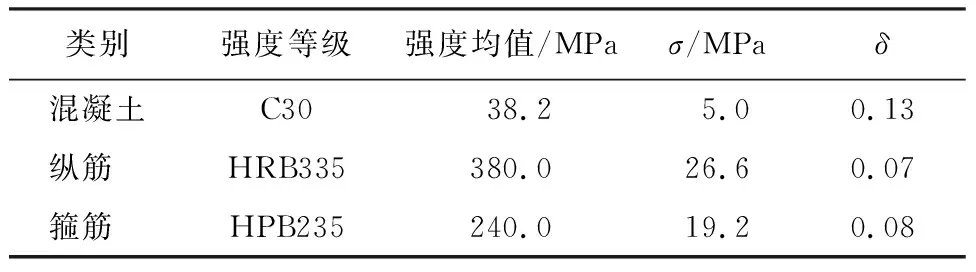
表3 混凝土及钢筋强度参数
结合表3中箍筋强度统计参数,再生混凝土梁及普通混凝土梁的所有统计参数汇总于表4、表5。其中再生混凝土梁抗拉强度由于考虑再生粗骨料的影响,其变异系数选用文献[24] 中的建议数值0.21,普通混凝土梁的数值则按照文献[11] 确定;截面尺寸的统计参数按照文献[30]确定。再生混凝土有腹筋梁的抗剪承载力公式不定性系数的均值和标准差采用上节的分析结果分别为1.41、0.17,普通混凝土梁则分别采用1.40、0.15。其中构件截面、恒载及计算模式不定性系数服从正态分布。

表4 再生混凝土梁参数汇总

表5 基准混凝土梁参数汇总
2.3 再生混凝土有腹筋梁抗剪承载力可靠指标计算方法
由于梁的剪切破坏属于脆性破坏,根据《建筑结构可靠性设计统一标准》[8](GB 50068—2018)中关于结构构件承载能力极限状态的可靠指标的规定,当安全等级为二级时,取β=3.7 作为可靠指标的判断依据。
3 再生混凝土有腹筋梁可靠指标计算及分析
结合文献[32]关于不同再生粗骨料取代率下的混凝土强度试验参数,取再生粗骨料取代率分别为30%、50%、70%、100%,剪跨比为1.5、2.0、3.0,配箍率为0.3%~2.5%,以此分析再生粗骨料取代率、剪跨比、配箍率对梁抗剪可靠指标的影响。
3.1 普通混凝土梁抗剪的可靠指标
荷载类型取100%永久荷载,不同剪跨比下普通混凝土梁的抗剪可靠指标结果如图4所示。
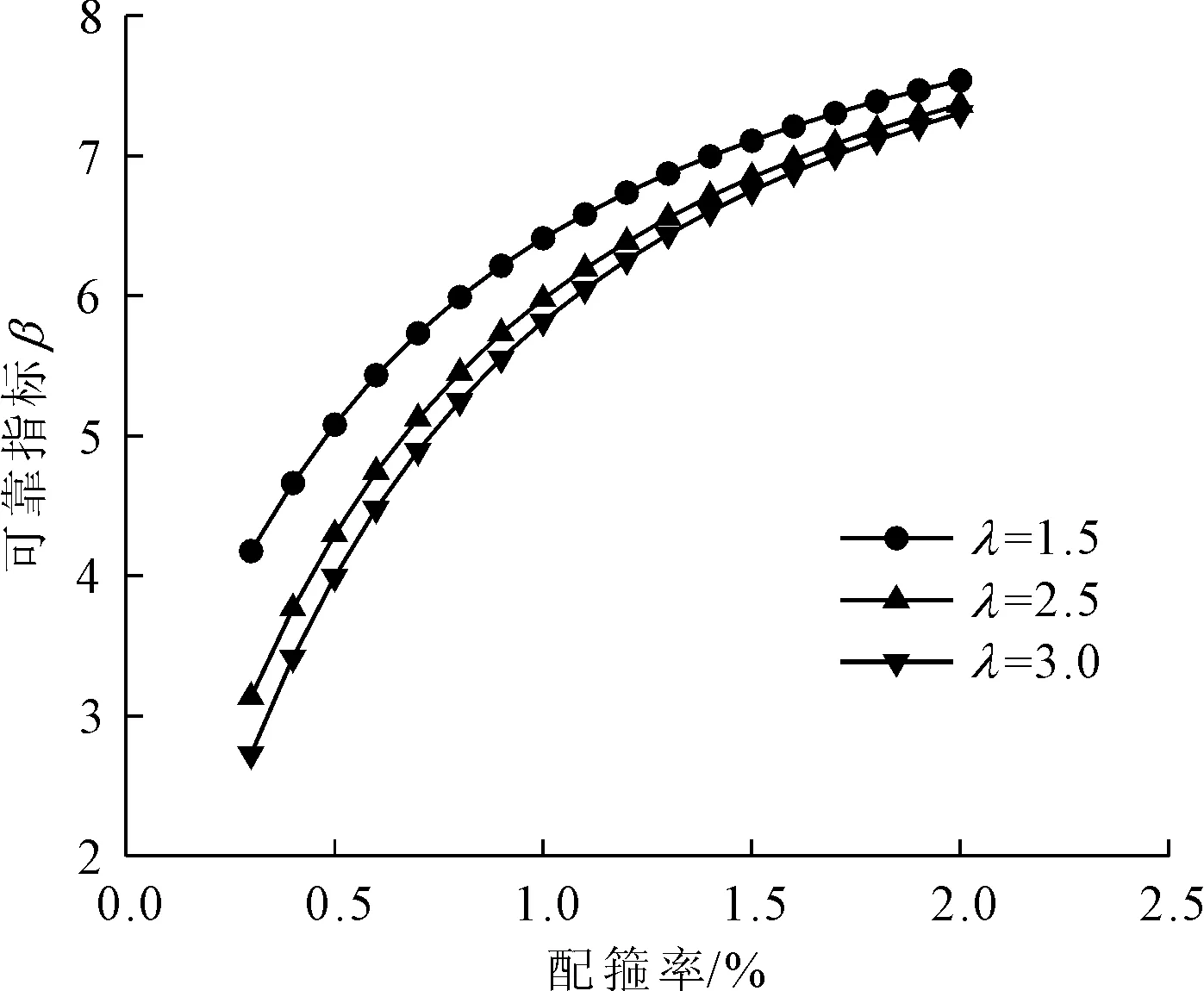
图4 剪跨比对普通混凝土梁可靠指标的影响
由图4可知随着配箍率的提高,梁抗剪可靠指标随着剪跨比的增大而增大,且各剪跨比之间的可靠指标差值逐渐减小;除了在配箍率ρsv=0.3%~0.4%,剪跨比λ=2.5、3时可靠指标不满足规范要求,其余均满足,可能原因是所采集的基准混凝土强度差异比较大,故变异性较大。鉴于λ为1.5时可靠指标最大,故下文对再生混凝土有腹筋梁的粗骨料取代率对可靠指标的影响情况分析时,取λ为1.5。
3.2 再生混凝土梁抗剪的可靠指标
3.2.1 再生粗骨料取代率对可靠指标的影响
对于再生混凝土梁,在配箍率为0.3%~2.5%的定区间下分别取再生粗骨料取代率为0%、30%、50%、70%、100%的五组数据进行分析,可靠指标在100%永久荷载作用下的可靠指标的变化情况如图5所示。由图5可以看出,再生混凝土梁的可靠指标随再生粗骨料取代率的增加而减小,其中当再生粗骨料取代率达到100%时可靠指标变化的幅度最大,随着配箍率的减小,可靠指标下降了60.1%;在再生粗骨料取代率为70%、100%时,再生混凝土有腹筋梁可靠指标在配箍率小于0.4%这个区间内小于规范要求,其余条件下均满足要求,故再生混凝土梁的取代率较高时,需适当增大配箍率使梁满足规范要求;掺入再生骨料后,可靠指标下降幅度较明显,下降幅度约在12.0%~33.9%之间,但不同再生混凝土梁取代率下可靠指标之间差异较小,且四者指标趋于一致,故再生粗骨料取代率的变化对于可靠指标的影响较小。主要原因在于再生粗骨料物理性质较差,颗粒整形使得骨料初始内部损伤增加,且表面附着的老砂浆使得混凝土在破坏时裂面展开情况更加复杂[33],从而导致再生混凝土梁在受剪时可靠指标下降。同时再生混凝土(不同取代率下)抗拉强度与普通混凝土相比下降明显,但不同取代率之间的再生混凝土抗拉强度差别不大,故在计算时各取代率下的再生混凝土梁可靠指标变化不大。
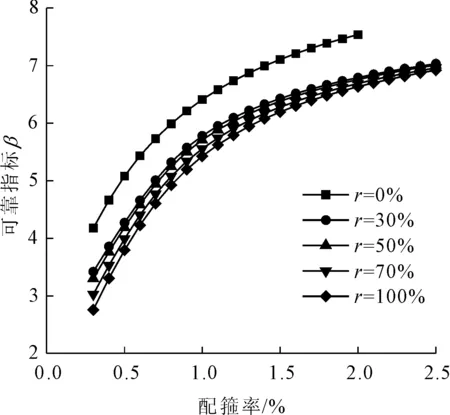
图5 不同粗骨料取代率下再生混凝土梁可靠指标的分布
3.2.2 剪跨比对可靠指标的影响
鉴于3.2.1节的分析结果,为了更符合工程实际,选取再生粗骨料取代率为30%,对于再生混凝土有腹筋梁,分别在配箍率为0.3%~2.5%的区间内取剪跨比为1.5、2.5、3.0的三组数据进行分析,三种不同剪跨在100%永久荷载作用下的可靠指标的变化情况如图6所示。从图中可以看出,当配箍率超过0.4%后,三种剪跨比下可靠指标均满足规范要求。随着配箍率的变化,再生混凝土梁的的可靠指标随剪跨比的减小而增大,可靠指标分别降低了63.8%、59.3%、51.3%。这是因为随着剪跨比的增大,再生混凝土梁的拱效应作用变弱,相对来说箍筋会比混凝土承担更多剪力,抑制斜裂缝开展的作用减弱,进而导致可靠指标降低[34]。当配箍率较小时,即在小于1.25%范围内,剪跨比λ取1.5时,可靠指标相较于λ取2.5、3.0时有了明显提升,最高达到25.7%,但随着配箍率的增大,剪跨比对可靠指标的提高作用减小,在配箍率达到2%以后,三种剪跨比对可靠指标的影响趋于一致。因此,当配箍率较低时可以适当减小剪跨比来满足可靠度要求。
为区别于图4普通混凝土梁在不同剪跨比下可靠指标的变化,图7表示在相同剪跨比下两种梁可靠指标之间的差异。从图中可以看出再生混凝土梁在同剪跨比下可靠指标小于普通混凝土梁,且随着配箍率的变大,两者之间可靠指标的差值也逐渐增大,剪跨比为1.5时再生混凝土梁相较于普通混凝土梁可靠指标的降低比剪跨比为2.5、3.0时明显,降幅在9.5%~18.0%之间,但大部分可靠指标也满足规范要求。
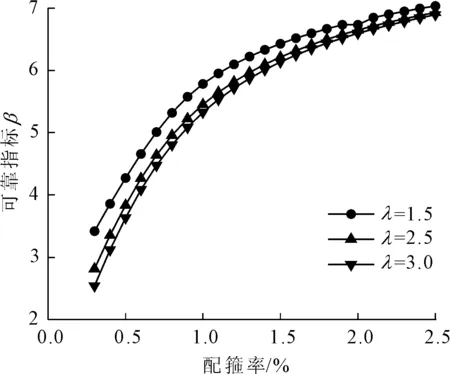
图6 不同剪跨比下再生混凝土梁可靠指标的分布
3.2.3 配箍率对可靠指标的影响
为使再生混凝土梁更好应用实际工程,选取再生粗骨料取代率为30%,剪跨比为1.5,分析不同配箍率再生混凝土梁可靠指标的分布情况,并对比普通混凝土梁,即图7(a)。由图7(a)可以看出不同配箍率下再生混凝土梁与普通混凝土梁整体变化趋势相同,且仅再生混凝土梁配箍率为0.3%时不满足可靠度要求,其余均符合规范标准。结合3.2.1节及3.2.2节的结果分析,再生混凝土梁的可靠指标在配箍率为0.3%~1.2%范围内增长幅度较大,增幅约43.9%,配箍率大于1.2%以后,对梁的可靠指标增长的贡献不明显,增幅约11.6%。且相比与再生混凝土取代率及剪跨比这些影响因素,配箍率对于混凝土梁的可靠指标的影响更大。其主要原因可能是箍筋在梁的受剪过程中承担了较多剪力,在抑制裂缝发展上发挥了较大作用[35]。
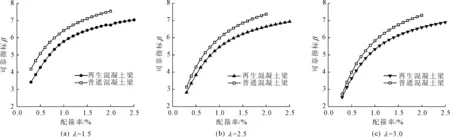
图7 相同剪跨比下两种不同混凝土梁可靠指标对比
4 结 论
(1) 再生混凝土梁的剪切破坏模式及抗剪承载力影响因素与普通混凝土梁一致,结合《混凝土结构设计规范》[11](GB 50010—2010),给出了考虑再生骨料取代率下的抗剪承载力公式,并确定再生混凝土梁承载力公式计算模式不定性系数的均值和方差分别为1.41和0.17。
(2) 在控制其他影响因素不变的情况下,再生混凝土梁的可靠指标随再生粗骨料取代率及剪跨比的增加而减小,随配箍率的增加而增加。但再生粗骨料取代率的变化对可靠指标影响较小,对于剪跨比而言,在配箍率小于1.25%的范围内减小剪跨比可以有效增大可靠指标。
(3) 利用验算点法与MATLAB相结合的方法,对再生混凝土梁抗剪承载力计算公式的可靠指标进行计算,大部分可靠指标满足规范对于梁剪切破坏时的可靠指标β不小于3.7的要求,表明在考虑再生粗骨料取代率影响因素下《混凝土结构设计规范》[11](GB 50010—2010)中普通混凝土梁抗剪承载力公式在实际再生混凝土结构工程中应用是可行的。

