直线三级倒立摆LQR控制稳定性的PSO-AFSA优化

武俊峰，郭旭飞

(1.黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022； 2.哈尔滨理工大学 自动化学院， 哈尔滨 150080)

0 引 言

倒立摆控制系统具有典型的快速性、不稳定性、多变性、强耦合性以及高阶次等特性[1]。通过倒立摆系统的控制研究可以有效解决譬如非线性、鲁棒性、随动性等问题，探究新型控制理论与智能算法的准确度及其在实践过程中的可行性，其中稳定性与抗干扰性是评估控制理论与控制方式是否有效的重要指标。作为经典的非线性控制系统，摆杆个数的增加致使倒立摆控制系统相对能控度的降低，直线二级倒立摆系统的相对能控度为0.008 2，而直线三级倒立摆系统的相对能控度则降低至0.004 6，相对能控度系数越小表明倒立摆系统各个变量之间的复杂程度越高，进而导致倒立摆系统越难控制[2]。近年来，众多学者对直线三级倒立摆控制系统进行了研究，提出了H_∞鲁棒控制、遗传神经网络控制、CGA优化改进型T-S模糊神经网络控制、RBF-ARX建模与云推理控制、模糊控制、参数自适应模糊PI控制等控制方法。LQR控制器作为现代控制理论中发展最早且相对更为成熟的状态空间设计方法，面对不同的控制系统都具备较强的鲁棒性以及较好的动态性能[3]。因此，笔者利用LQR控制算法原理对直线三级倒立摆控制系统设计LQR控制器，采用PSO-AFSA算法优化加权系数，通过系统模型仿真验证PSO-AFSA算法优化参数对于直线三级倒立摆系统动态稳定性以及抗干扰性的提升效果。

1 系统物理模型

为了简化直线三级倒立摆控制系统，忽略空气阻力与各种摩擦力的影响，将摆杆认定为刚体。直线三级倒立摆的结构模型如图1所示。小车质量mc为1.096 kg，摆杆m1质量为0.05 kg，摆杆2质量m2为0.06 kg，摆杆3质量m3为0.13 kg，摆杆1中心到转动中心的距离L1为0.077 5 m，摆杆2中心到转动中心的距离L2为0.10 m，摆杆3中心到转动中心的距离L3为0.25 m，摆杆1与竖直方向的夹角为θ1，摆杆2与竖直方向的夹角为θ2，摆杆3与竖直方向的夹角为θ3。

利用拉格朗日推导运动学方程，拉格朗日方程为

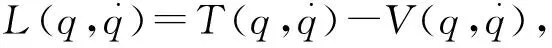
式中：L——拉格朗日算子；

Q——系统的广义坐标；

T——系统的动能；

V——系统的势能。

图1 直线三级倒立摆物理模型 Fig. 1 Physical model of Three-stage inverted pendulum

式中：Fi——系统在第i个广义坐标上的外力，i=1,2,3,…,n；

x、θ1、θ2、θ3——系统的广义坐标。

(1)

将式(1)在平衡位置附近进行泰勒级数展开，线性化得

式中，kij——Fi对其第j个变量的偏微分系数。

通过Mathematics程序运算可得系统的状态方程：

(2)

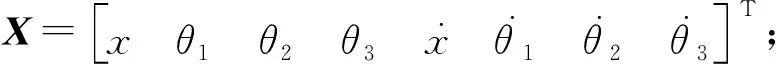
A=

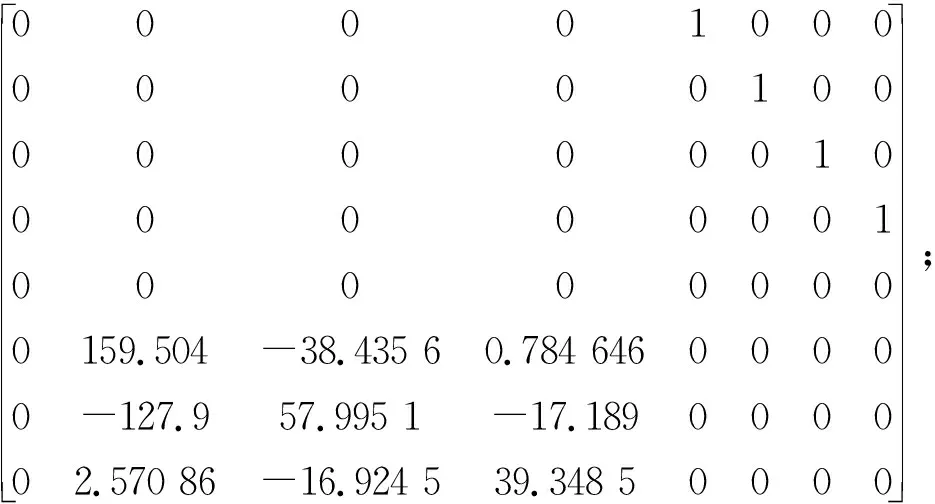
B=[0 0 0 0 1 6.649 04

-0.158 31 0.003 182 11]T；

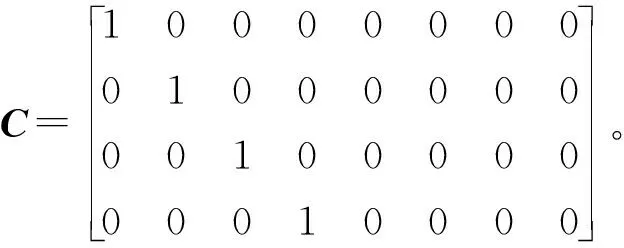
分析式(2)可以发现，作为自然不稳定系统的直线三级倒立摆，其状态与输出均是可控的，同时系统具有可观测性。但是直线三级倒立摆控制系统不具收敛性，需要设计控制器对系统进行稳定控制[3]。

2 LQR控制算法

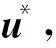
系统的性能指标J的表达式为

(3)

式中：Q——状态变量的加权矩阵；

R——输入变量的加权矩阵；

tf——终止时间；

t0——初始时间；

S——约束条件。

由式(3)可知，直线三级倒立摆控制系统有8个状态变量、1个输入变量。由于直线三级倒立摆控制系统是单输入系统，因此，R矩阵可以设定为1。LQR控制器中的Q矩阵对角线上各个权重系数分别表示控制系统中各项指标误差的相对重要性；R表示能量损耗的相对重要性，主要用于限制控制器的输出量，以防输出量过大造成系统无法得到有效控制。LQR控制器中Q矩阵的参数选取对于控制系统而言至为关键，对其控制性能影响最大。然而由于直线三级倒立摆控制系统的高阶次特性，导致无法通过对直线三级倒立摆控制系统的分析实现Q和R矩阵各个权重系数范围的初步确定。因此，需要根据仿真模型输出的动态响应曲线判断Q矩阵中各个权重系数大小对直线三级倒立摆控制系统的影响。

根据LQR控制器加权系数选取经验可知，通常情况下Q矩阵中各个主要控制变量对应的加权参数偏大，同时在一定限度内，Q矩阵中的权值越大，控制系统到达平衡状态所需时间越短。在直线三级倒立摆控制系统中，小车位移、摆杆1角度、摆杆2角度以及摆杆3角度为主控变量，因此，忽略Q矩阵中q5、q6、q7、q8等4个权重变量对直线三级倒立摆控制系统造成的影响，设置为0。选取不同的Q矩阵参数，经过多次仿真实验，通过直线三级倒立摆控制系统输出的动态响应曲线变化情况可以发现，q1和q2对直线三级倒立摆控制系统x、θ1、θ2、θ34个变量响应状态的影响远大于q3和q4对控制系统变量造成的影响，并且q3对于直线三级倒立摆控制系统的影响程度高于q4，其规律可以描述为q1,q2>q3>q4。按照上述规律，利用仿真试凑法，综合考虑多种影响因素，选取LQR控制器的Q为

运行程序得到直线三级倒立摆状态方程的状态反馈增益矩阵为

K=[-22.360 7 254.349 9 -363.089 3871.216 8 -31.477 0 12.990 4-21.923 6 137.756 1]。

3 PSO-AFSA算法

人工鱼群算法(AFSA)与粒子群算法(PSO)均属于群体智能算法。人工鱼群算法(AFSA)模拟鱼群的觅食、聚群、追尾、随机等主要行为，跳出局部极值的寻优能力强，但是迭代速度慢[5]。粒子群算法(PSO)模仿鸟群的觅食行为，快速收敛能力强且简单可行，但是算法后期跳出局部最优值的能力弱[6]。PSO-AFSA融合PSO与AFSA双方的优势，PSO粒子的飞行速度属性可以加快人工鱼群的收敛速度，PSO粒子的惯性权重属性能够增强人工鱼群承载速度的能力[7]。精英鱼群的设立能够有效融合PSO与AFSA算法的特性进而提升综合算法的收敛性。PSO-AFSA算法优化流程如图2所示。

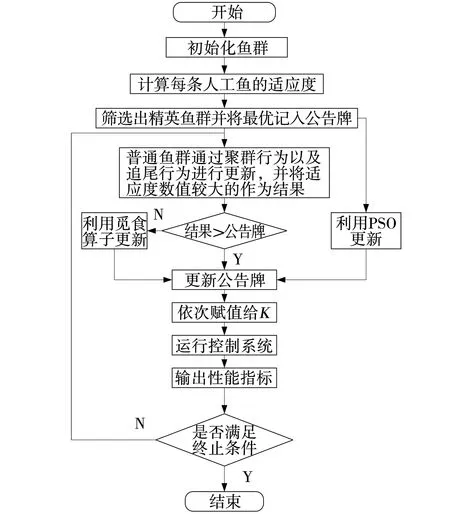
图2 PSO-AFSA算法优化流程Fig. 2 PSO-AFSA algorithm optimization flow

(1)随机初始化N条人工鱼，设置人工鱼群的视野V、步长S、拥挤度因子δ、最大尝试次数Nt、外部最大迭代次数Nmax等参数。

(2)通过运算得出每条人工鱼的适应度数值J，挑选出Ne个满足条件的人工鱼组成精英鱼群，其余人工鱼定义为普通鱼群Xn，筛选出适应度数值最大的J计入公告牌Jb。

(3)利用PSO算法更新Xe，在PSO内部进行nmax次循环寻优。

(4)利用AFSA中的聚群及追尾行为更新Xn，选取适应度数值较大的作为更新结果进行下一步操作。

(5)比较J以及Jb的数值大小，判定适应度数值J是否变化，若数值增大则更新Jb；若数值减小则利用觅食算子Fp更新Xn。

(6)计算更新后的Xe及Xn的所对应的适应度，并与公告牌Jb进行大小对比，如果数值增大，则将其数值赋给公告牌Jb。

(7)当所有的人工鱼更新完成，判定是否达到终止条件，若达到终止条件则输出最后确定的最优化适应度数值Jb，算法流程结束[8]。

适应度函数LQR的性能指标为

(4)

PSO-AFSA仿真过程中各个参数设置为：人工鱼数量100、最大迭代次数500、觅食最大尝试次数50、精英鱼群数量50、PSO内部循环次数10、惯性权重1.5、拥挤度因子0.618、移动步长0.2、飞行速度[-1，1]、视野1。通过PSO-AFSA算法优化后的加权矩阵Q为对角矩阵其值分别为1 792.56、1 153.55、976.95、695.16、13.53、7.27、35.84、22.37，加权矩阵R为1。

4 仿真实验

设置直线三级倒立摆控制系统各个状态量的初始值为

摆杆1的初始角度设置为0.05 rad，摆杆2的初始角度设置为-0.05 rad，摆杆3的初始角度设置为0.05 rad，仿真时间设置为10 s，仿真步长设置为0.02，运行直线三级倒立摆仿真模型获取小车位移仿真响应曲线如图3所示。

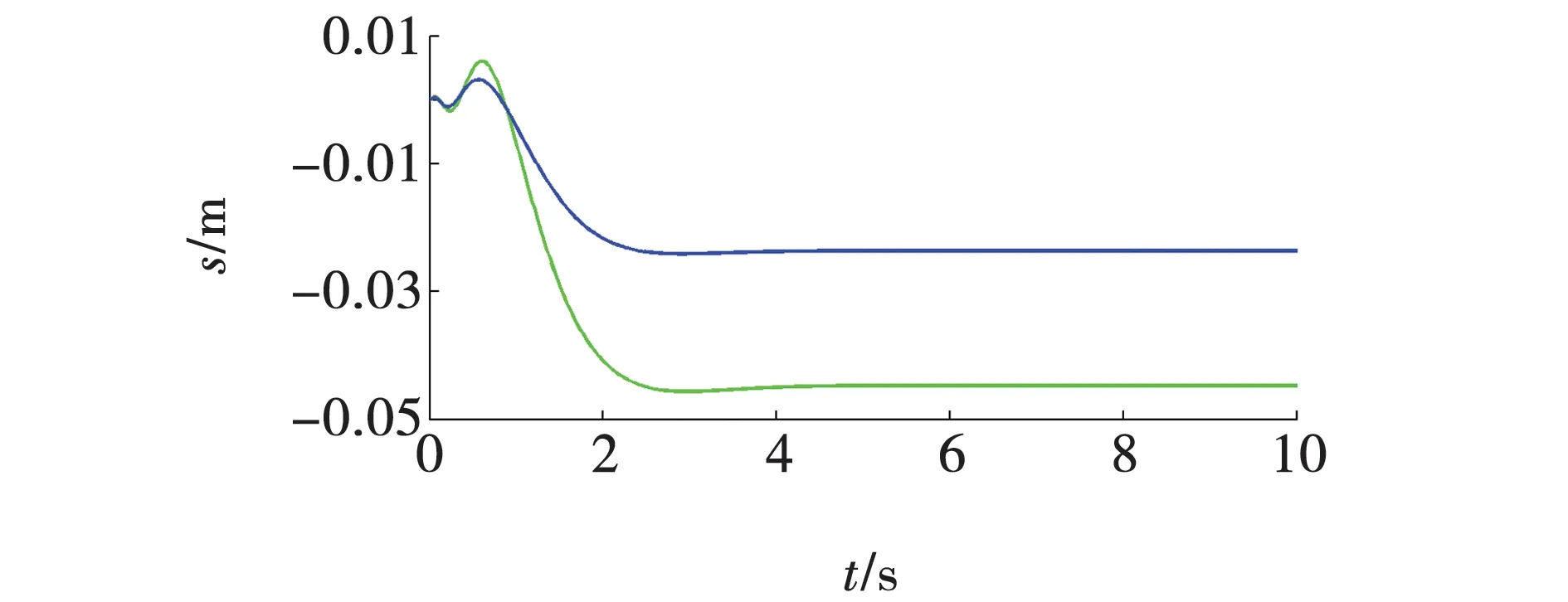
图3 PSO-AFSA优化前后小车位移仿真对比曲线Fig. 3 Comparison curve of carriage shift simulation before and after PSO-AFSA optimization

通过图3可以看出，PSO-AFSA算法优化后的直线三级倒立摆小车位移的超调量明显减少，表明系统平衡性增强。

摆杆1、2、3角度的仿真响应曲线如图4所示。

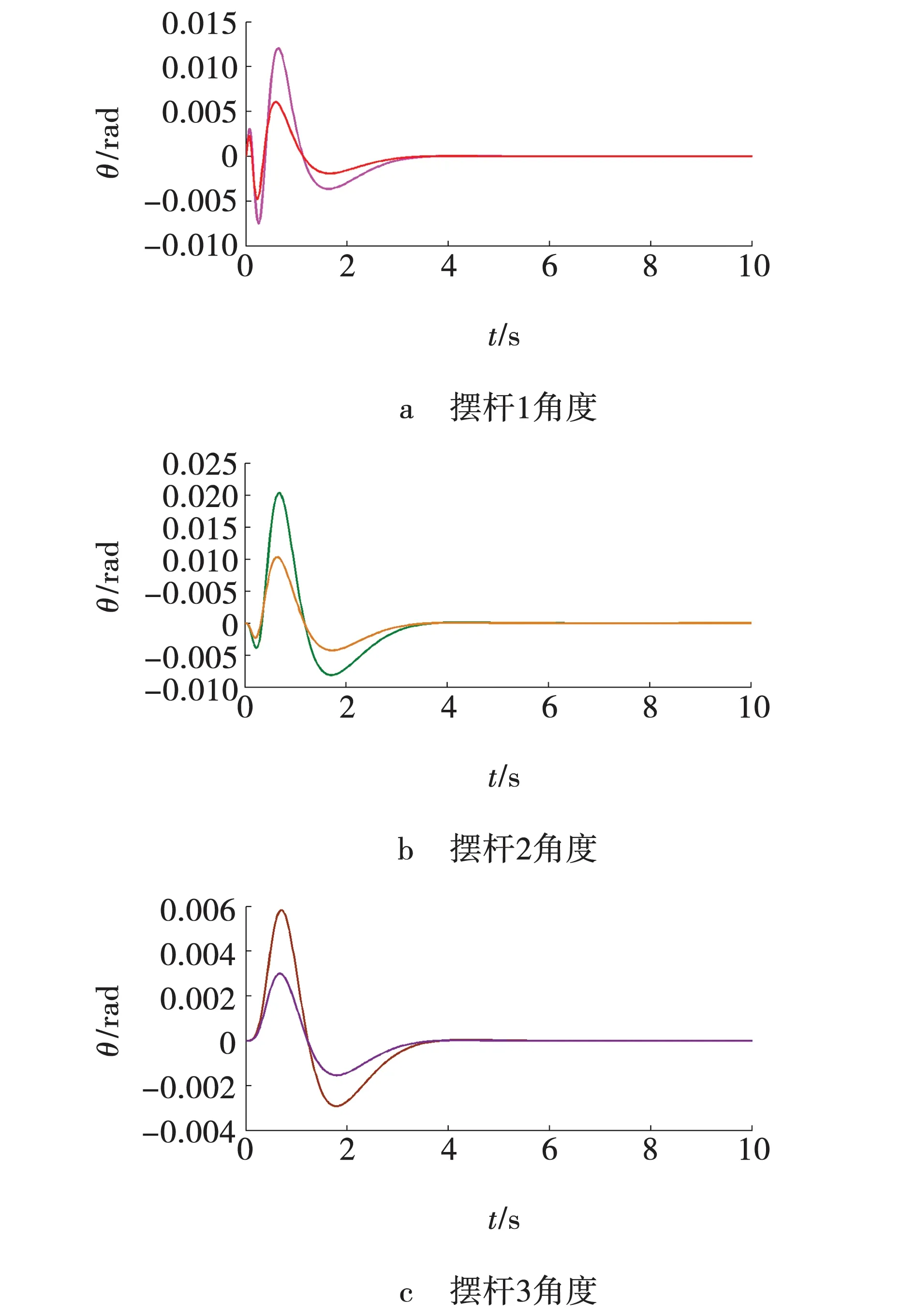
图4 PSO-AFSA优化前后摆杆1、2、3角度仿真对比曲线Fig. 4 Comparison curve of 1、2、3 angle simulation of PSO-AFSA optimized pendulum bar

由图4可以看出，PSO-AFSA算法优化后的直线三级倒立摆摆杆1、2、3角度的超调量明显减少，曲线更加平滑，系统稳定性增强。

综上所述，PSO-AFSA优化后的直线三级倒立摆控制系统中摆杆1、摆杆2和摆杆3的超调量明显减少，同时具有较好的稳定性；PSO-AFSA优化前系统到达平衡位置需要大约4.0 s的时间，PSO-AFSA优化后系统到达动态平衡位置约3.2 s，表明PSO-AFSA算法优化后的直线三级倒立摆控制系统受到干扰后，经过一定时间可以更快地达到动态平衡，抗干扰能力更强。

5 结束语

针对直线三级倒立摆系统设计的LQR控制器基本实现了对系统的有效控制。直线三级倒立摆控制系统中的小车位移、摆杆1、2、3角度等状态变量从不同的初始位置开始，经过约4.0 s时间的调节后趋向于动态稳定平衡，同时具有较强的抗干扰能力。而PSO-AFSA算法优化后的直线三级倒立摆控制系统的各个变量超调量明显减少，系统更加稳定，同时达到动态平衡的时间大约缩减为3.2 s，表明系统的稳定性以及抗干扰性更强。通过仿真验证了PSO-AFSA融合算法在优化直线三级倒立摆控制系统性能方面的可行性以及有效性。因此，可以在文中的基础上对直线三级倒立摆实物进行实时控制，检验智能算法优化高维度控制系统在实践方面的可行性以及有效性。