运动参数对碟盘刀具破碎煤岩载荷的影响

刘春生, 李鑫鹏，刘延婷

(1.黑龙江科技大学， 哈尔滨 150022； 2.黑龙江科技大学 机械工程学院，哈尔滨 150022； 3.黑龙江科技大学 安全工程学院， 哈尔滨 150022)

0 引 言

提高机械破碎煤岩的效率对矿山开采具有重大意义。国内外学者对破碎煤岩做了诸多研究。Su等[1]从理论、数值模拟和实验回归分析了截齿破岩切削力峰值均值，指出三者之间的强相关性。Loui等[2]对截齿破碎岩石进行数值模拟与实验，得出了切削深度、截齿磨损和岩石性质对切削力的影响。Van Wyk等[3]利用离散单元法对比分析了不同刀具切削岩石的理论、模拟和实验的切削力峰值均值，得出数值模拟应考虑切削深度和刀具磨损的影响。Ushakov等[4]提出了一种沿外摆线多点冲击破岩的新方法，建立了转速与冲击频率的运动方程，可保证载荷均匀分布。Prokopenko等[5]数值模拟了不同直径和长度截齿破岩，给出最优参数的截齿强度。程永亮[6]通过双滚刀切削岩石的数值模拟和实验，探究了贯入度对比能耗的影响。翟淑芳等[7]运用广义粒子动力学法(GPD法)数值模拟了TBM滚刀破岩，实验验证了GDP法的有效性，给出了节理和高围压对破岩的影响。祝效华等[8]通过模拟PDC切削齿动态破岩，给出切削厚度、温度和后倾角等与切削齿破岩效率的关系。刘春生等[9-12]通过单齿与碟盘刀具破碎煤岩的单因素和正交数值模拟，根据统计方法、小波能量熵和功效系数法等分析了其运动和结构参数对煤岩的破碎效果的影响。因此，笔者利用ABAQUS软件正交数值模拟不同运动参数下碟盘刀具破碎煤岩，通过方差分析法综合分析碟盘刀具3运动参数的影响作用，对进给速度、振动幅值和频率与载荷之间进行多元非线性拟合，优化碟盘刀具运动参数。

1 正交数值模拟

1.1 方案设计

利用ABAQUS软件建立碟盘刀具破碎煤岩模型[13]，碟盘刀具为刚性材料，半径150 mm，楔面角度45°，刀刃半径3 mm。煤岩采用Drucker-Prager塑性本构模型，其长宽高分别为420、280和120 mm，切削厚度18 mm，密度1.5×10-9t/mm3，弹性模量1 400 MPa，泊松比0.3，抗压强度30 MPa。基于碟盘刀具的进给速度v、振动幅值A和频率f设计3参数5水平25组正交数值模拟，其具体工况如表1所示。

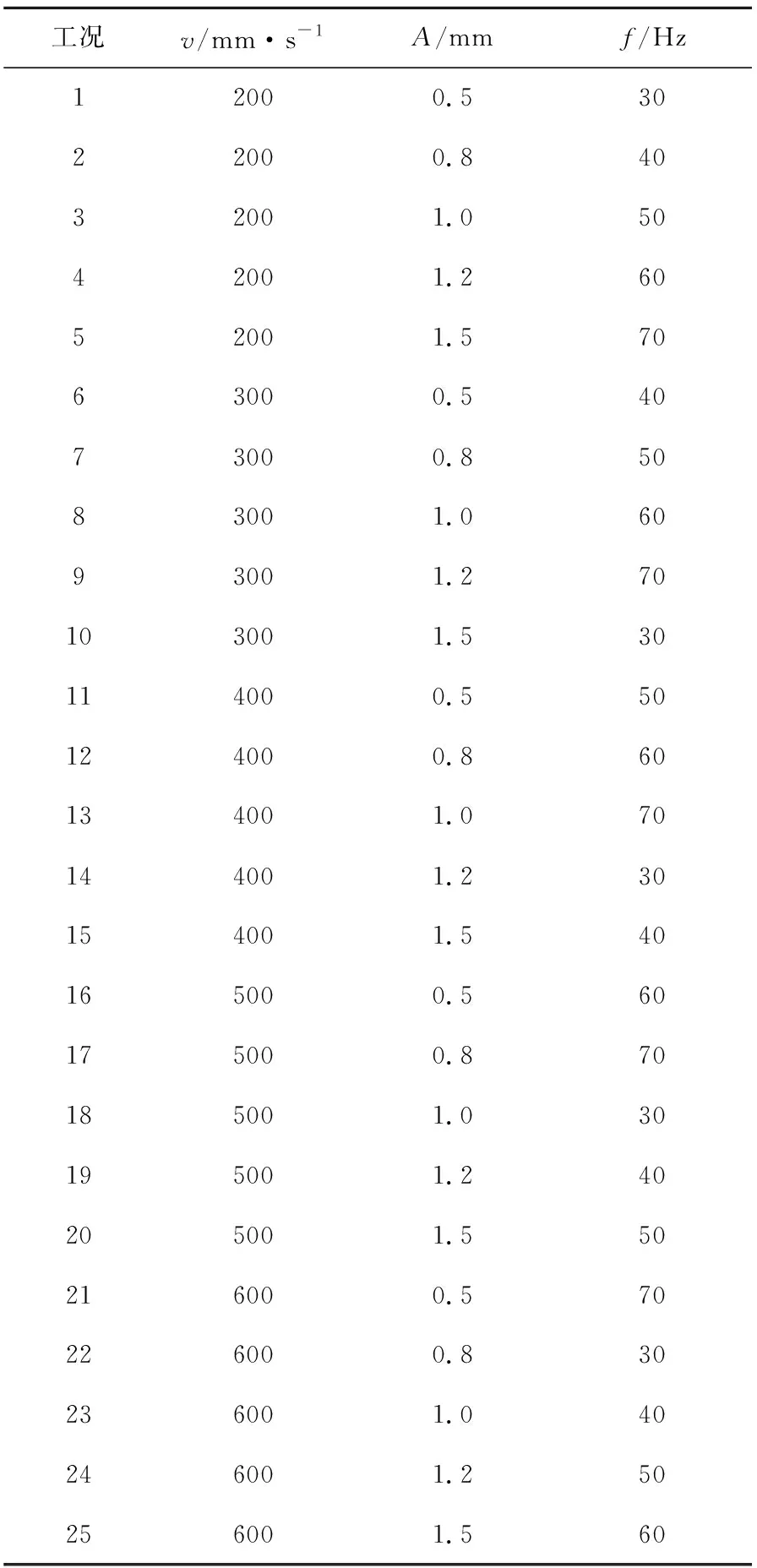
表1 25组工况具体参数

1.2 典型工况结果分析

碟盘刀具在典型工况5、10、15、20、25的数值模拟应力云图结果，如图1所示。由图1可知，复合运动破碎煤岩的应力分布，刀具向上运动时在同一位置节点处的Mises应力云图，碟盘刀具主要受力点在刀齿处和刀盘两侧，碟盘刀具进行破碎煤岩时其应力云图形成月牙状，应力损伤面积从中间向两侧逐渐减小，应力损伤面积受进给速度的影响较大，工况25时速度最大，应力损伤面积也最大。5种工况下碟盘刀具径向载荷与轴向载荷矢量叠加的总载荷，如图2所示。由图2可知，工况5时，由于进给速度相比于其他4种最小且频率最高，其总载荷明显小于另外4种工况，其他4种在振幅相同的情况，不同进给速度和频率相互组合后载荷大小差异较小。

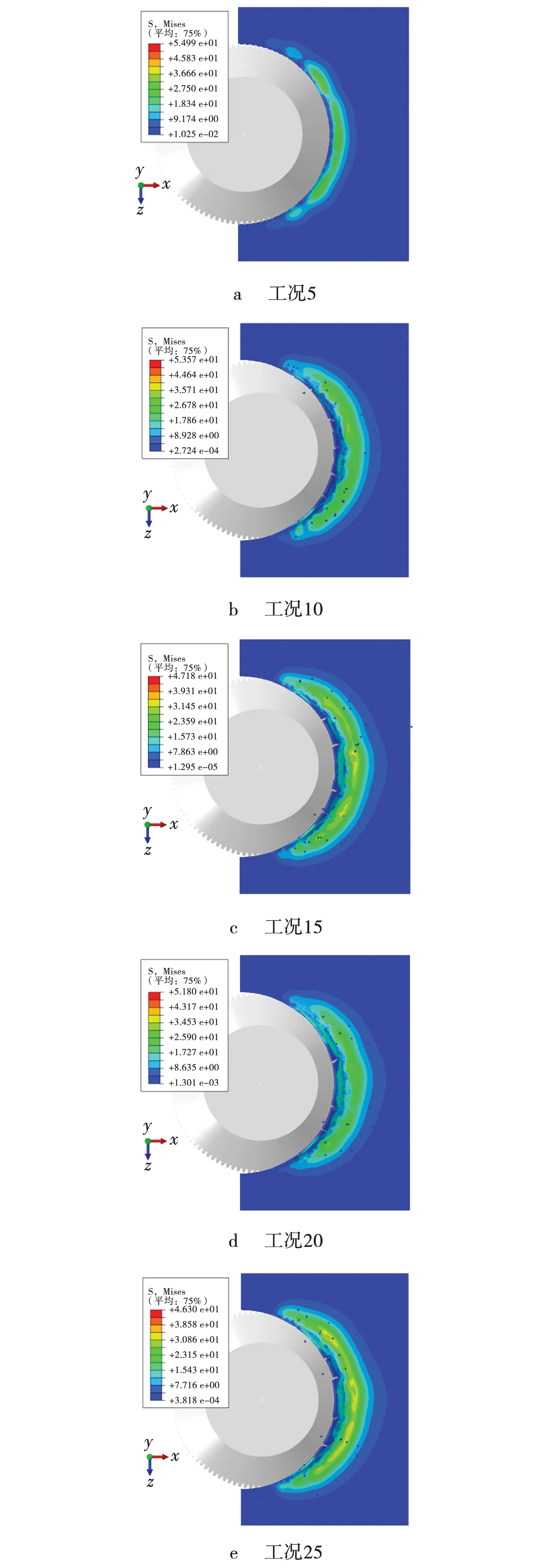
图1 典型工况的应力云图Fig. 1 Stress nephogram for typical operating conditions

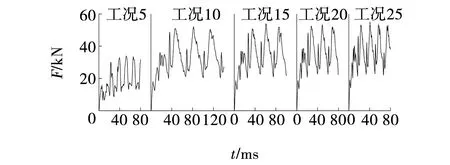
图2 典型工况的总载荷Fig. 2 Total load at typical operating conditions

2 破碎性能的方差分析

2.1 方差分析

方差分析法分为单因素方差分析法和多因素方差分析法。采用多因素方差分析法分析正交数值模拟结果。多因素方差分析法是研究两个及两个以上因素对评价指标的显著影响，该方法不仅能分析各因素的独立影响，还能分析多个因素交互作用下产生的显著影响，从而得到最优因素组合[14]。

根据差方和的加和性，总差方和Qz等于各因素的差方和与由随机误差引起的数值模拟误差的差方和Qe的总和，得

Qz=Q1+Q2+Q3+Qe，

(1)

(2)

Qz是25组数值模拟结果的总差方和，反映其结果的总体差异，数值越大，则各实验结果之间的差异越大。Qb是各因素的差方和，b等于1、2、3时，表示进给速度、振动幅值和频率的差方和。

(3)

(4)

式中，Yab——第b个因素的第a个水平的响应值之和。

(5)

式中：yac——第a个水平第c次实验的响应值；

m——单个因素的总水平数；

u——每个水平的数值模拟的总次数。

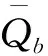
(6)

(7)

式(6)中的Tb与式(7)中的Te分别是各因素和数值模拟误差的自由度，为一组参数可自由取值的个数

Tz=mu-1，

(8)

Tb=m-1，

(9)

(10)

式中，Tz——数值模拟的总自由度。

为了反映各因素对评价指标的影响程度，用各因素的平均差分和与实验误差平均差分和之比I值衡量：

(11)

给定置信度h，从统计分布数值表的F分布中找到临界值Ih(Tb、Te)。将计算的I值与临界值比较，若I>Ih(Tb、Te)，则该因素对评价指标的影响显著，并且两者之间的差值越大，该因素的显著性越大。

2.2 计算结果

将文献[11]中的14组响应值分别代入其进行计算，得出14组响应值的方差分析I值，如表2所示。

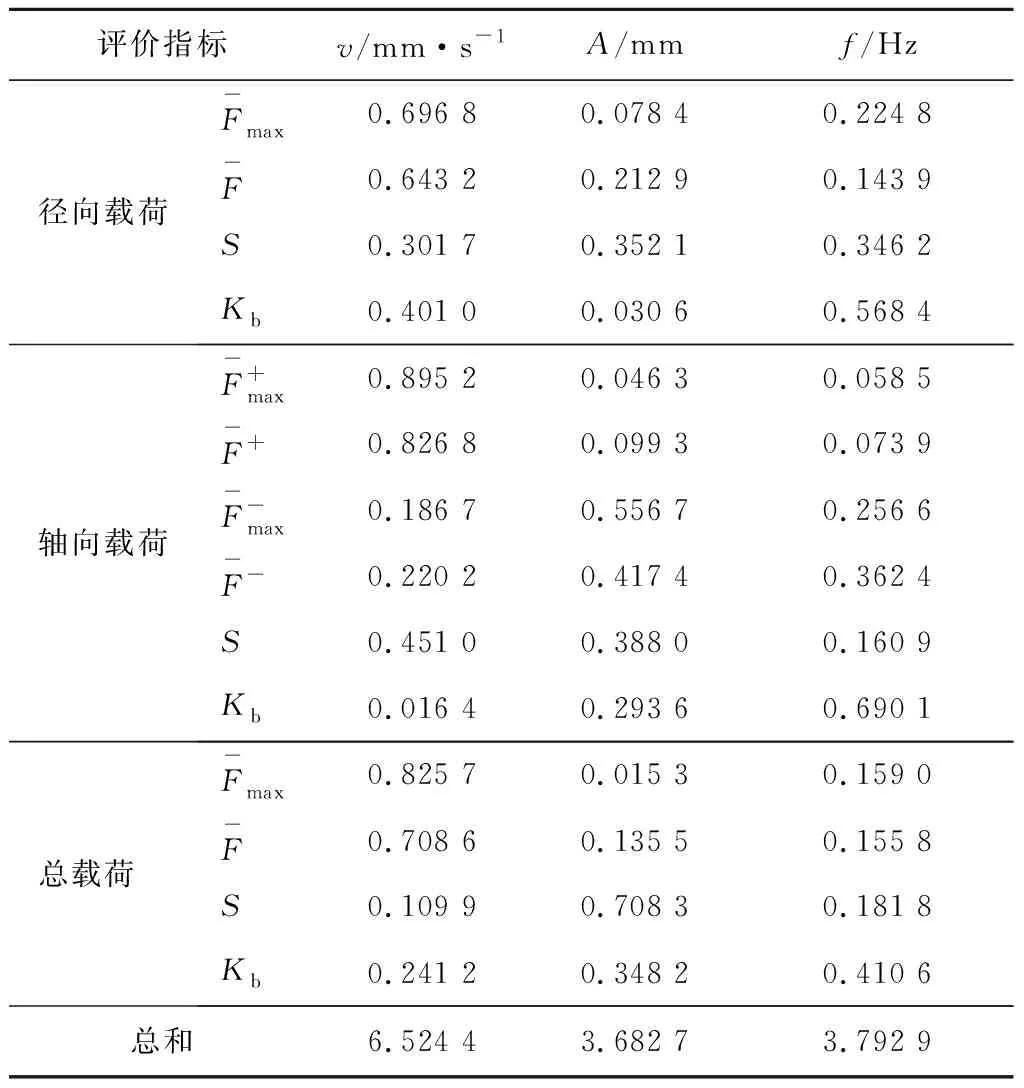
表2 各参数的影响程度

通过进给速度、振幅和频率对载荷影响程度结果分析对比，发现进给速度相比于振幅和频率对载荷的影响较显著，但振幅对负轴向载荷的影响略大；振幅和频率主要对载荷的小波能量熵S和盒维数Kb影响较大。据表2可知，3参数对碟盘刀具破碎煤岩性能的显著性影响占比不同，进给速度、振幅和频率分别占46.60%、26.31%和27.09%，故进给速度对碟盘刀具破碎性能的影响显著，其次是频率，最后是振幅，应优先控制进给速度大小。

3 载荷的多元非线性拟合模型

3.1 峰值均值

基于有限元数值模拟结果，得出了进给速度、振幅和频率三个运动参数对碟盘刀具破碎煤岩载荷的影响，将表1中的v、A和f作为自变量，将文献[11]中的径向载荷、轴向载荷及总载荷的稳定段峰值均值作为因变量，拟合数学关系式

(12)

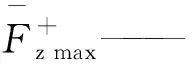
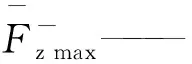
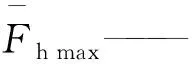
径向、轴向及总载荷峰值均值的数值模拟值与拟合值，如图3所示。通过对比分析拟合值和模拟值的结果，可发现径向、正轴向、负轴向和总载荷拟合值与模拟值之间的平均误差分别为2.66%、2.42%、13.22%和2.37%。不同工况下，径向、正轴向和总载荷的拟合值的变化趋势与其模拟值变化趋势基本一致，且平均误差低，负轴向载荷的平均误差受个别奇异点的影响相对较大，但模拟值与拟合值变化趋势也相似，具有较高的重合度，故载荷的峰值均值拟合公式能很好地反映不同工况载荷值。

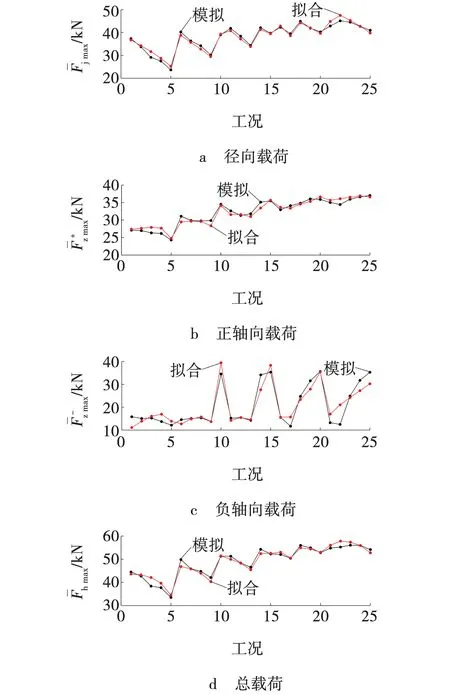
图3 数值模拟与多元拟合载荷峰值均值Fig. 3 Numerical simulation and multivariate fitting load peak mean value

振幅、频率和进给速度对总载荷峰值均值的影响，如图4所示。由图4a可知，当v=300 mm/s、f=30～70 Hz、A=0.5～1.5 mm时，随幅值和频率减小，总载荷峰值均值增大；由图4b可知，当v=200～600 mm/s、f=30～70 Hz、A=1.0 mm时，总载荷峰值均值随进给速度增大而增大，随频率增大而减小；由图4c可知，当v=200～600 mm/s、f=50 Hz、A=0.5～1.5 mm时，总载荷峰值均值随进给速度增大而增大。

当A=1.0 mm、f=50 Hz时，径向、正轴向、负轴向和总载荷峰值均值的拟合值均与进给速度呈正比，如图5a所示。当v=300 mm/s、f=50 Hz时，径向载荷峰值均值的拟合值与振幅呈反比，而正、负轴向载荷峰值均值的拟合值与振幅呈正比，总载荷拟合值随振幅增加而略微减小，如图5b所示。当v=300 mm/s、A=1.0 mm时，径向、正轴向、负轴向和总载荷峰值均值的拟合值均与频率呈反比，如图5c所示。

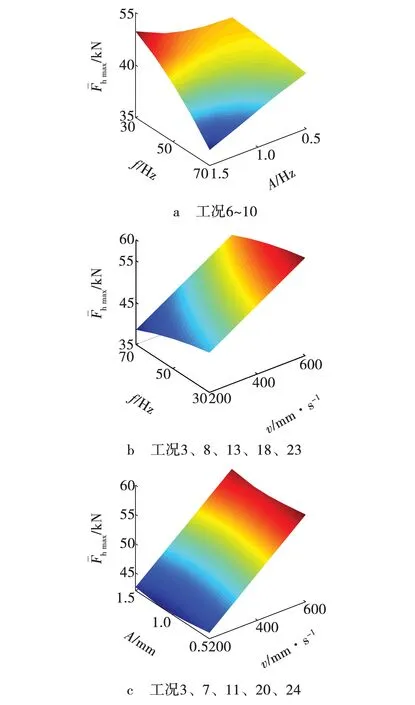
图4 振幅、频率和进给速度对总载荷峰值均值的影响 Fig. 4 Influence of amplitude and frequency on mean value of peak load

3.2 载荷谱均值

将表1中的v、A和f作为自变量，文献[11]的径向载荷、轴向载荷及总载荷曲线均值作为因变量，拟合数学关系式：

(13)

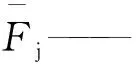
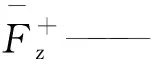
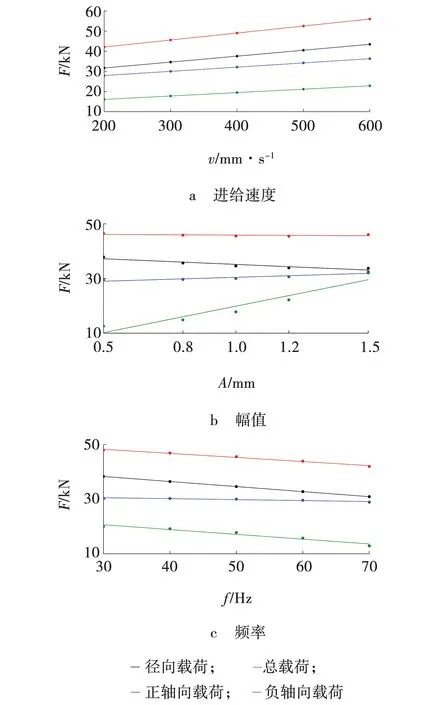
图5 单个参数对载荷峰值均值的影响Fig. 5 Influence of single parameter on mean value of peak load

径向载荷、正轴向载荷、负轴向载荷及总载荷谱均值的真实值与拟合值，如图6所示。通过对比分析载荷谱均值的拟合值与模拟值的结果，可发现径向、正轴向、负轴向和总载荷拟合值与模拟值之间的误差范围分别为3.36%、2.78%、13.12%和3.13%。不同工况下，三向载荷的拟合值的变化趋势与其模拟值变化趋势基本一致，且平均误差低，没有出现偏离度较大的数据点，具有较大的重合度，其曲线均值拟合公式能很好地反映载荷的变化趋势与大小。

振幅、频率和进给速度对总载荷谱均值的影响，如图7所示。由图7a可知，当v=300 mm/s、f=30～70 Hz、A=0.5～1.5 mm时，总载荷谱均值随频率减小而增大，随幅值减小而增大；由图7b可知，当v=200～600 mm/s、f=30～70 Hz、A=1.0 mm时，总载荷谱均值随进给速度增大而增大，随频率增大而减小；由图7c可知，当v=200～600 mm/s、f=50 Hz、A=0.5～1.5 mm时，总载荷谱均值随进给速度增大而增大，随振幅增大而减小。

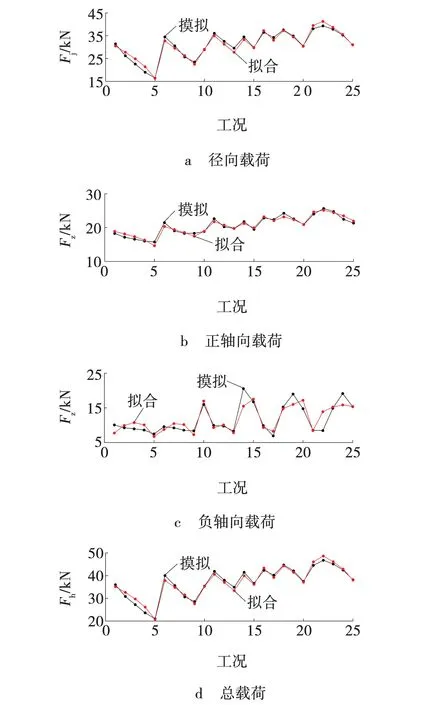
图6 数值模拟与多元拟合载荷曲线均值Fig. 6 Numerical simulation and multivariate fitting load curve mean value

当A=1.0 mm、f=50 Hz时，径向、轴向和总载荷谱均值的拟合值均随进给速度增大而增大，如图8a所示。当取定v=300 mm/s、f=50 Hz时，径向和正轴向载荷的载荷谱均值的拟合值随振幅增大而减小比，而负轴向载荷的载荷谱均值的拟合值与振幅呈正比，总载荷拟合值随振幅增加而略微减小，如图8b所示。当v=300 mm/s、A=1.0 mm时，径向、正轴向、负轴向和总载荷谱均值的拟合值均随频率增大而减小，如图8c所示。

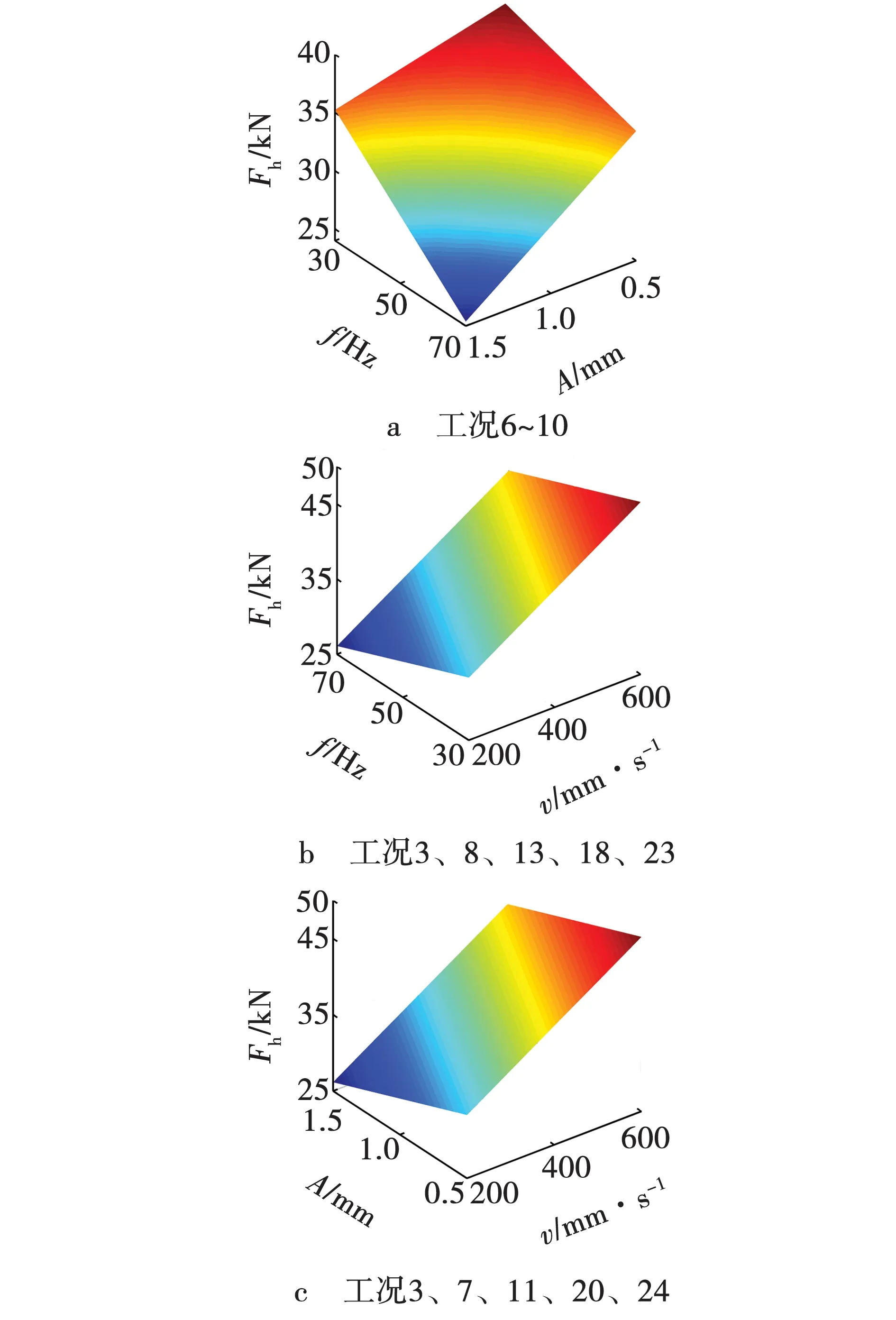
图7 振幅、频率和进给速度对总载荷谱均值的影响Fig. 7 Influence of amplitude frequency and feed velocity on mean value of total load spectrum

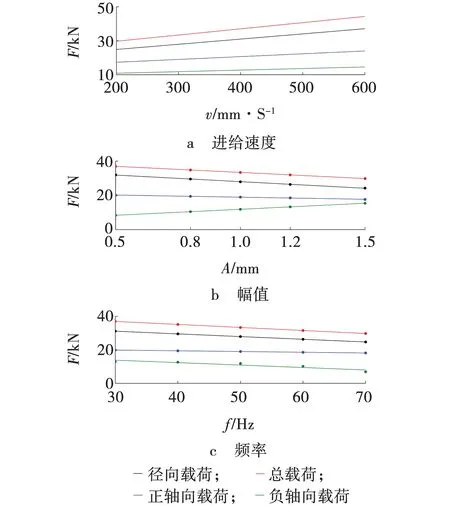
图8 单个参数对载荷峰值均值的影响 Fig. 8 Influence of single parameter on mean value of peak load

4 典型工况的能量分析

能量输出经常是ABAQUS分析的一个重要部分。煤岩崩落前发生最大的能量变化有内能和动能，其中内能为

Eu=EE+EP+ECD+EA，

(14)

式中：EE——可恢复弹性应变能;

EP——非弹性(如塑性)耗散能;

ECD——蠕变或者粘弹性耗散能;

EA——伪应变能。

典型工况下的输出能量进行如图9所示。由图9a可知，五种不同工况下的内能变化，可看出内能变化趋势相同，相同时间进给速度越大其内能越大；由图9b可知，五种不同工况下的动能的变化，随着频率的增大，动能的波动越来越大，在一定频率范围内，随着进给速度的增加，动能逐渐增加，但当频率超过一定范围后，动能的变化不仅受到进给速度的影响，还受到频率的影响，工况5下，进给速度为200 mm/s，由于70 Hz的高频率，使其动能会高于工况10和15下的动能。

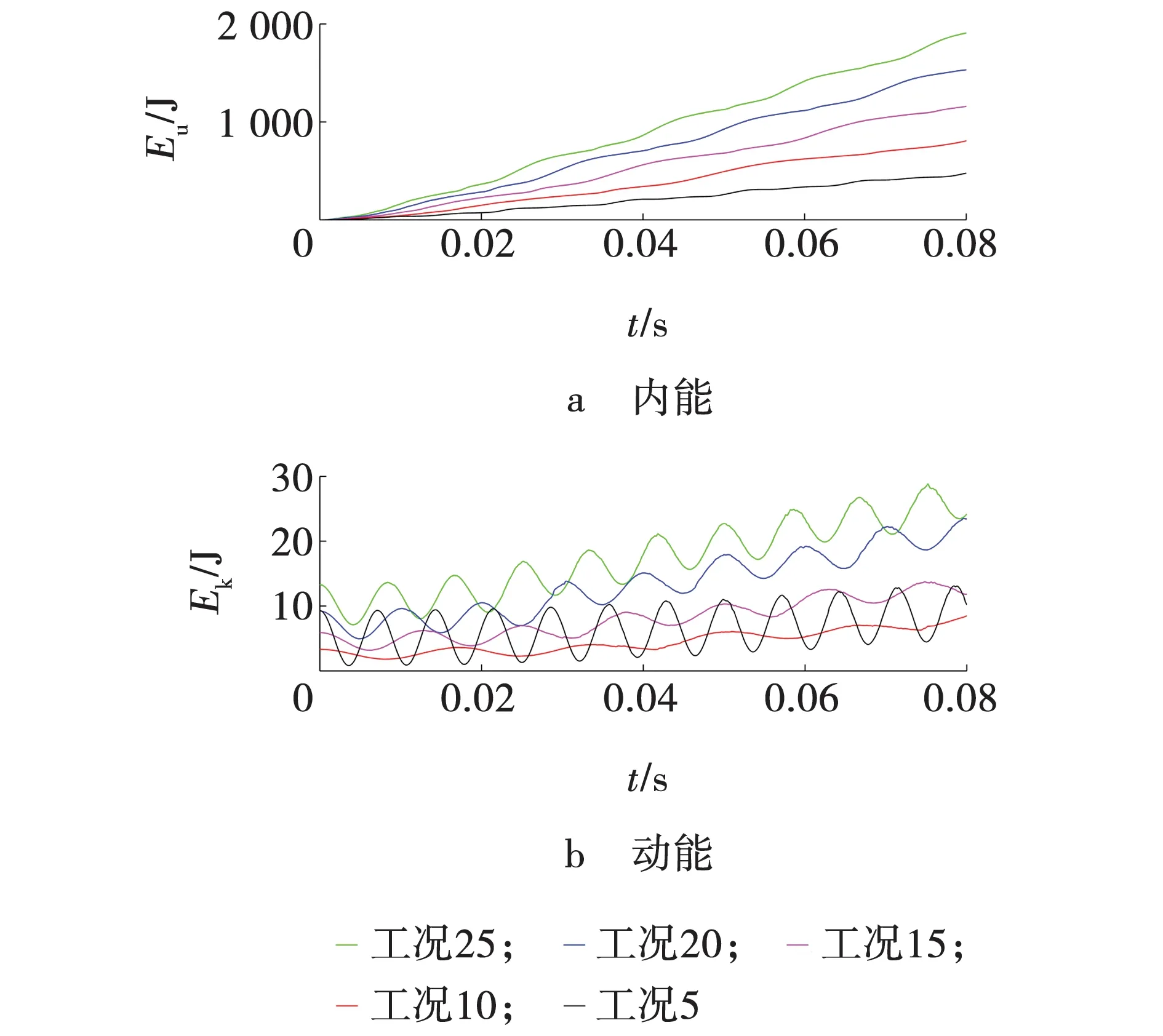
图9 典型工况下的输出能量Fig. 9 Output energy under typical working conditions

5 结 论

(1) 由3参数5水平的25组正交数值模拟结果的方差分析可得，进给速度、振动幅值和频率对碟盘刀具破碎性能影响占比分别为46.60%、26.31%和27.09%，若想提高碟盘刀具破碎性能，可依次调整进给速度、振动频率和幅值。

(2) 通过多元非线性拟合，建立碟盘刀具径向载荷、轴向载荷和总载荷与进给速度、振动幅值和频率之间的关系模型，其关系模型计算所得的拟合值与数值模拟值的误差均值均在15%以内，故拟合关系式能很好地给出不同工况下的载荷值。

(3) 给出了碟盘刀具载荷随运动参数变化的变化趋势，随进给速度增大，碟盘刀具总载荷增大；振幅增大，总载荷减小；频率增大，总载荷减小。

(4) 通过能量分析，给出了内能和动能随着运动参数变化的趋势，随着进给速度增大，内能逐渐增大，在幅值不变且频率在30～60 Hz的范围内，动能随着进给速度增大逐渐增大，当频率达到70 Hz时，动能会受到影响。