泛化神经网络算法的RC柱恢复力预测方法

王 涛，周天楠，孟丽岩

(黑龙江科技大学 建筑工程学院， 哈尔滨 150022)

0 引 言

模型更新技术是一种提高混合试验中非线性数值子结构模型精度的有效手段，主要包括基于模型的参数识别方法和不基于模型的神经网络方法。王涛[1]采用UKF算法对弹簧及防屈曲支撑构件进行了在线参数识别及构件层次模型更新，完成了一系列模型更新混合试验验证，有效提高了混合试验精度。陈永盛[2]和梅竹[3]分别针对截面恢复力模型和材料层次模型进行了在线参数识别，扩展了混合试验应用能力。参数识别精度不仅依赖于识别算法本身精度，也会依赖于假定数值模型的准确程度。

恢复力模型误差是不可避免的，发展不基于模型的预测算法将会是一种新的解决途径。神经网络算法因其无需预先知晓模型参数等优势而受到研究者们的青睐。Yang等[4]首次将神经网络应用于模型更新混合试验中。Elanwar等[5]利用离线的神经网络算法识别了两跨钢框架的双折线本构模型。王燕华等[6]提出了一种基于遗忘因子和 LMBP 神经网络的混合试验在线模型更新方法，并对一个两自由度非线性结构进行了模型更新混合试验数值模拟验证。Yun等[7-8]增补了神经网络的输入变量，将原来的三变量变为五变量，通过神经网络算法得到了循环荷载下结构材料层面的滞回性能，研究了梁柱节点的性质。王涛等[9-11]提出一种在线神经网络算法，并应用于结构混合试验中。

已有研究一般要求神经网络训练与预测具有相同的构件对象，如何预测具有不同性能参数的结构恢复力，是一个需要解决的难题。在不同轴压比、纵筋配筋率、体积配箍率及长细比情况下的RC柱具有不同的恢复力模型，笔者提出一种泛化神经网络算法，以预测不同参数RC柱恢复力，通过单参数变化和多参数变化情况下数值模拟验证算法的预测精度和泛化性能。

1 方法原理

图1 含有两个隐含层的泛化神经网络算法拓扑结构Fig. 1 Topological structure of generalized neural network algorithm with two hidden layers

K=1+fyhρs/σc，

(1)

式中：fyh——箍筋屈服强度；

ρs——试件的体积配箍率；

σc——为混凝土28 d圆柱体抗压强度，建议取混凝土轴心抗压强度。

分别考虑了单参数变化情况和由截面尺寸不同引起η、ρ、K和λ四参数变化的情况，

η=l0/b，

(2)

式中：l0——柱子的计算长度；

b——截面宽度b与截面高度h中的较小值。

ρ=∑niAi/(bh)，

(3)

式中：ni——纵向钢筋根数；

Ai——与ni对应的纵向钢筋截面面积。

ρsv=∑niliAsi/(Acs)，

(4)

式中：ni——箍筋的肢数；

Asi——单肢箍筋截面面积；

li——混凝土核心面积内的长度；

Ac——核心区混凝土面积，Ac=(b-2c)(h-2c)；

c——混凝土保护层厚度；

s——箍筋间距。

λ=N/(fcbh)，

(5)

式中，N——轴向力设计值。

可见，当仅改变截面尺寸b×h时，四个结构参数将同时发生改变。分别对神经网络进行训练和恢复力预测，以验证神经网络算法预测精度和所构造网络的泛化性能。网络输入样本为

(6)

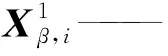
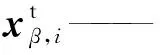
n——训练样本的批次数。

式(6)中等式右侧的第i列可以展开为

(7)

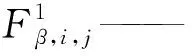
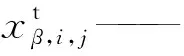
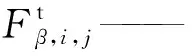
m——第i训练批次下样本个数，文中所有训练批次下样本个数均相同。

将所有训练批次下训练样本全部输入BP神经网络，进行一次性训练。该方法扩展了神经网络的输入变量的选取范围，可以使得算法能够预测同一构件不同结构参数下的恢复力，从而可以提高神经网络结构本身的泛化能力。

2 数值模拟

2.1 选取对象

为了验证所提出的泛化神经网络算法RC柱恢复力预测方法的有效性，以2011年钢筋混凝土整体框架拟静力倒塌试验盲测竞赛的中柱C作为研究对象[12]。约束混凝土强度增强系数K为1.3时柱子的尺寸及配筋形式示意图如图2所示。柱子所采用混凝土实测立方体抗压强度为30.1 MPa，纵向受力钢筋采用四种等级为HRB335的钢筋，直径分别为10、8、6、4 mm,对应的实测屈服强度分别为481、582、441、390 MPa。箍筋采用等级为HPB235的直径为6 mm的钢筋，其实测屈服强度为441 MPa。所采用的材料强度取值选自于2011年钢筋混凝土整体框架拟静力倒塌试验盲测竞赛[13-14]。采用OpenSees软件对中柱C进行建模，通过数值模拟生成多组训练样本，并通过利用所提出的泛化神经网络算法进行预测，从而获得RC柱的预测恢复力。

图2 K=1.3时构件尺寸及配筋形式示意Fig. 2 Schematic of component size and reinforcement form of K= 1.3

2.2 不同参数下恢复力预测

利用不同长细比，不同纵筋配筋率，不同体积配箍率，不同轴压比以及不同截面尺寸的柱子有限元模拟结果数据形成观测样本，并对BP神经网络进行离线训练。神经网络拓扑结构包含两个隐含层，每层各含有15个神经元，第一层的激活函数采用双曲正切函数tansig，第二层的激活函数采用双曲对数函数logsig。设置一个输出层，输出变量为下一步的恢复力，其中输出层的激活函数采用纯线性函数purelin。神经网络训练方法选用LM-BP算法，神经网络的训练参数为目标函数采用均方差，最大训练步数为50步，目标误差为10-4。

采用均方根误差指标评价RC柱恢复力预测精度，计算公式为

(8)

式中：ek——第k步的预测恢复力均方根误差；

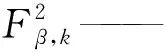
yβ,k——第k步柱恢复力预测值。

2.2.1 滞回曲线

长细比、纵筋配筋率、体积配箍率以及轴压比是四种影响RC柱恢复力的主要结构参数。为了验证所提出的算法预测RC柱恢复力的有效性，文中分别对仅考虑改变单一参数和考虑不同截面尺寸即四种结构参数同时改变情况下的RC柱恢复力进行预测。

为了验证不同长细比η时的恢复力预测精度，将长细比η为9.6、12.0、15.0、18.0、24.0时的柱位移和恢复力数据构成神经网络五变量输入变量，预测长细比η分别为9.0、9.6、15.0、21.0、27.0时柱恢复力，柱滞回曲线如图3所示。由图3a～e可以看出，所提出的神经网络算法在预测不同长细比下RC柱恢复力时，滞回曲线均具有较高的拟合程度。

为了验证不同纵筋配筋率ρ时的恢复力预测精度，将纵筋配筋率ρ为0.423 9%、0.518 1%、0.675 1%、0.753 6%、0.894 9%时的柱位移和恢复力数据构成神经网络五变量输入变量，预测纵筋配筋率ρ分别为0.376 8%、0.423 9%、0.533 8%、0.675 1%、1.177 5%时柱恢复力。柱滞回曲线如图4所示。由图4a～e可以看出，所提出的神经网络算法在预测不同纵筋配筋率下RC柱恢复力时，滞回曲线均具有较高的拟合程度。

为了验证不同约束混凝土强度增强系数K，即不同体积配箍率影响下时的恢复力预测精度，将系数K为1.3、1.4、1.6、1.7、1.8时的柱位移和恢复力数据构成神经网络五变量输入变量，预测系数K分别为1.2、1.3、1.5、1.7、1.9时柱恢复力。柱滞回曲线如图5所示。由图5a～e可以看出，所提出的神经网络算法在预测不同约束混凝土强度增强系数下RC柱恢复力时，滞回曲线均具有较高的拟合程度。

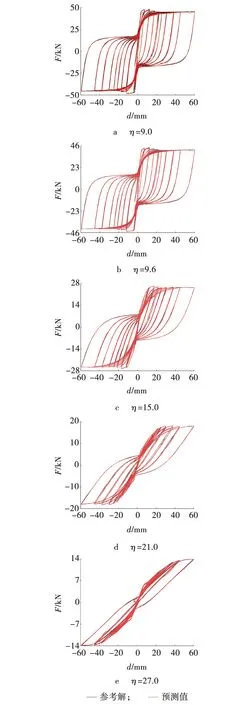
图3 不同长细比时预测所得滞回曲线 Fig. 3 Predicted hysteresis curves with different slenderness ratios

图4 不同纵筋配筋率时预测所得滞回曲线 Fig. 4 Predicted hysteresis curves with different reinforcement ratios

为了验证不同轴压比λ时的恢复力预测精度，将轴压比λ为0.02、0.03、0.04、0.06、0.07时的柱位移和恢复力数据构成神经网络五变量输入变量，预测轴压比λ分别为0.01、0.02、0.05、0.06、0.08时柱恢复力。柱滞回曲线如图6所示。由图6a～e可以看出，所提出的神经网络算法在预测不同轴压比下RC柱恢复力时，滞回曲线均具有较高的拟合程度。

为了验证不同截面尺寸时，即此时长细比η、纵筋配筋率ρ、约束混凝土强度增强系数K，即受体积配箍率影响、轴压比λ四个参数均同时发生变化时的恢复力预测精度。以b×h分别为200 mm×250 mm、200 mm×300 mm、200 mm×400 mm、250 mm×250 mm、200 mm×400 mm时的柱位移和恢复力数据构成神经网络五变量输入变量，预测b×h分别为200 mm×200 mm、200 mm×300 mm、200 mm×400 mm、250 mm×300 mm、300 mm×300 mm时柱恢复力。各截面尺寸下的四种结构参数值如表1所示。柱滞回曲线如图7所示。

由图7a～e可以看出，所提出的神经网络算法在预测不同截面尺寸下RC柱恢复力时，滞回曲线均具有较高的拟合程度。

随着长细比的不断增加，滞回曲线的面积不断减小，表明构件柱的延性变差，耗能能力降低；随着纵筋配筋率或体积配箍率的不断提高，滞回曲线的面积不断增加，表明构件柱的延性增加，耗能能力提高；随着轴压比的不断增大，滞回曲线的面积不断减小，表明构件柱的延性变差，耗能能力降低。

由以上分析可见，随着四种结构参数的改变，RC柱的滞回曲线均发生了不同程度的变化。采用所提出的算法在预测RC柱恢复力时能较完全的模拟出不同结构参数下滞回曲线的变化趋势，且所得预测值与参考解具有较好的拟合程度，说明该算法具有较高的预测精度和泛化能力。

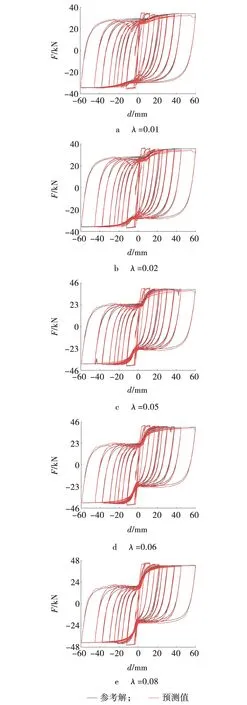
图6 不同轴压比时预测所得滞回曲线 Fig. 6 Predicted hysteresis curves with different axial compression ratios

图7 不同截面尺寸时预测所得滞回曲线 Fig. 7 Predicted hysteresis curves for different section sizes

2.2.2 误差分析

不同长细比下RC柱恢复力误差曲线如图8所示。由图8可知，1 000步以后均方根误差取值范围在0.01到0.05之间，误差较小。在1 000步以后的各均方根误差中，η=9.0时神经网络所预测的恢复力误差最大，其收敛时的均方根误差约为0.025 35。均方根误差最终收敛时的最小值出现在η=15.0时，此时的均方根误差约为0.010 24，说明预测结果具有一定的精度。对于不同的长细比，所构造的神经网络结构在预测长细比参数下的恢复力时体现出良好的泛化性能。

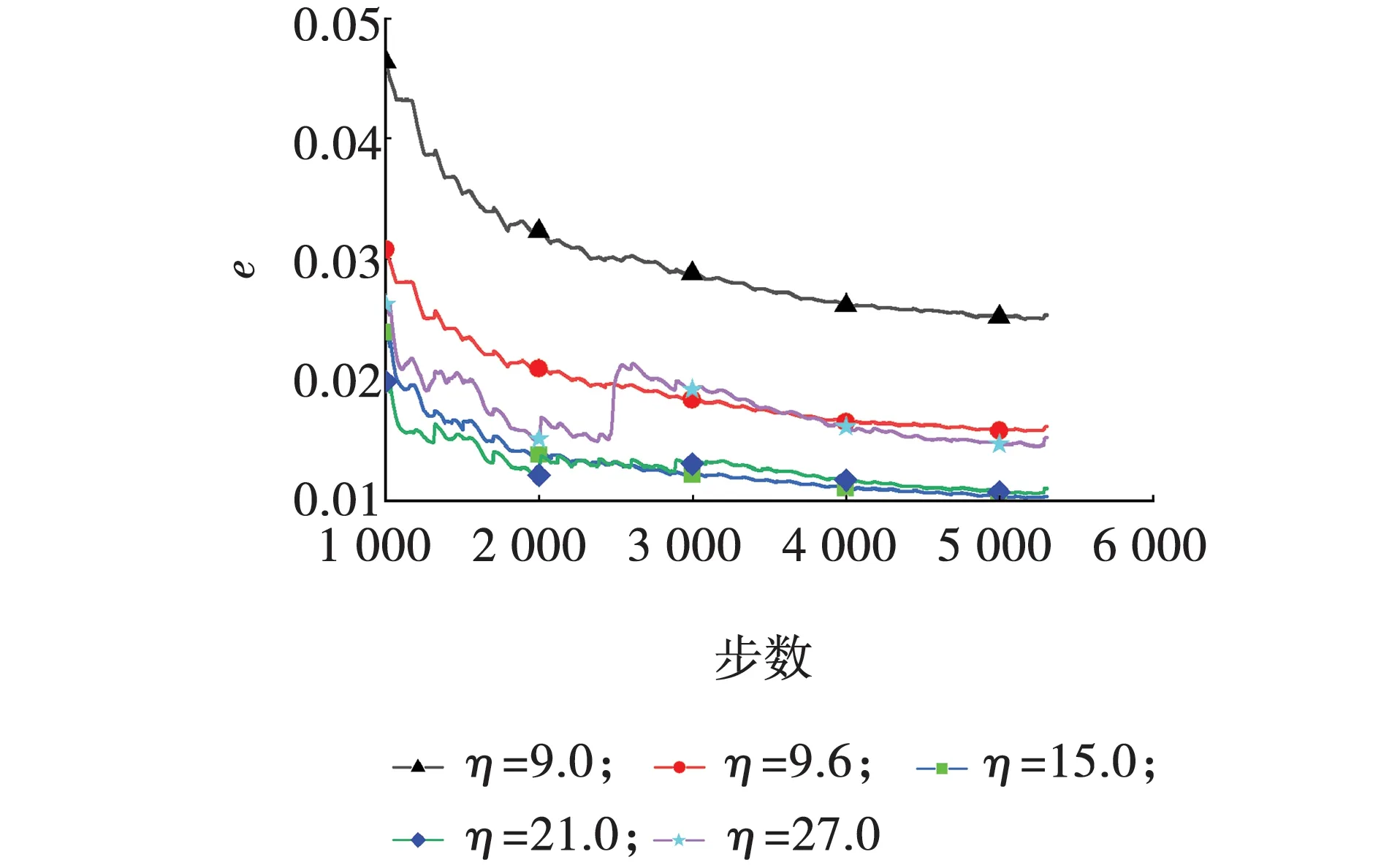
图8 不同长细比时误差对比Fig. 8 Error comparison of different slenderness ratios

不同纵筋配筋率下RC柱恢复力误差曲线如图9所示。

图9 不同纵筋配筋率时误差对比 Fig. 9 Error comparison of different longitudinal reinforcement ratio

由图9可知，1 000步以后均方根误差取值范围在0.006到0.016之间，误差较小。在1 000步以后的各均方根误差中，ρ=0.423 9%时神经网络所预测出的恢复力误差最大，其收敛时的均方根误差约为0.010 79。均方根误差最终收敛时的最小值出现在ρ=0.675 1%时，此时的均方根误差约为0.006 01，说明预测结果具有一定的精度。对于不同的纵筋配筋率，所构造的神经网络结构在预测纵筋配筋率参数下的恢复力时体现出良好的泛化性能。

不同约束混凝凝土强度增强系数下RC柱恢复力误差曲线如图10所示。由图10可知，1 000步以后均方根误差取值范围在0.012到0.020之间，误差较小。在1 000步以后的各均方根误差中，K=1.2时神经网络所预测出的恢复力误差最大，其收敛时的均方根误差约为0.015 97。均方根误差最终收敛时的最小值出现在K=1.5时，此时的均方根误差约为0.012 66，说明预测结果具有一定的精度。对于不同的约束混凝土增强系数，即不同的体积配箍率，所构造的神经网络在预测体积配箍率参数下的恢复力时体现出良好的泛化性能。

图10 不同约束混凝土强度增强系数时误差对比Fig. 10 Error comparison of different confined concrete strength enhancement coefficients

不同轴压比下RC柱恢复力误差曲线如图11所示。由图11可知，1 000步以后均方根误差取值范围在0.03到0.06之间，误差较小。在1 000步以后的各均方根误差中，λ=0.01时神经网络所预测出的恢复力误差始终最大，最终收敛时的均方根误差约为0.049 16。均方根误差最终收敛时的最小值出现在λ=0.05时，此时的均方根误差约为0.037 81。说明预测结果具有一定的精度。不同轴压比时恢复力的预测效果较好。对于不同轴压比，所构造的神经网络在预测轴压比参数下的恢复力时体现出良好的泛化性能。

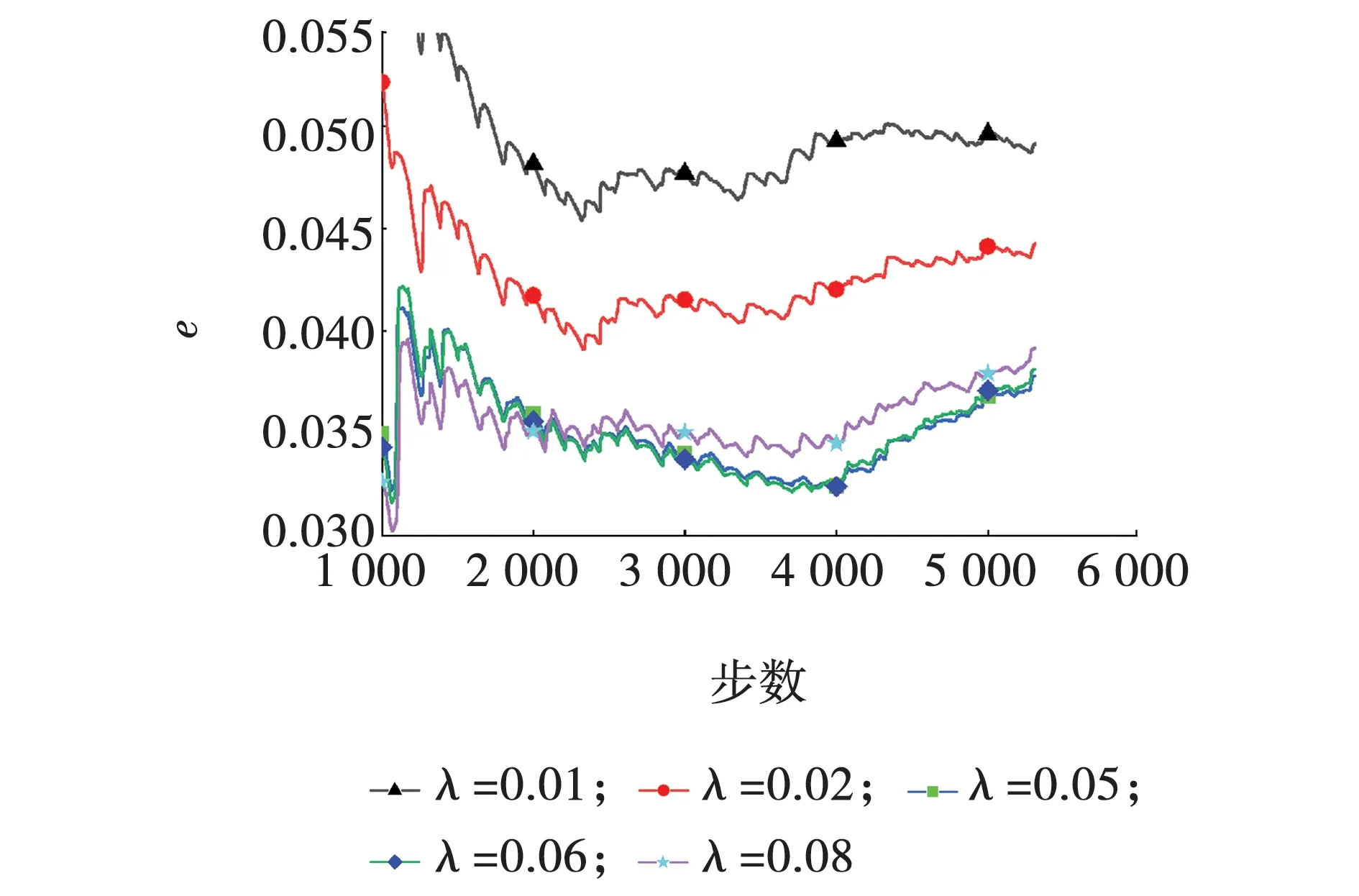
图11 不同轴压比时误差对比 Fig. 11 Error comparison of different axial compression ratios

不同截面尺寸下RC柱恢复力误差曲线如图12所示。由图12可知，1 000步以后均方根误差取值范围在0到0.035之间，误差较小。在1 000步以后的各均方根误差中，截面尺寸为250 mm×300 mm时神经网络所预测出的恢复力误差始终最大，最终收敛时的均方根误差约为0.023 47；均方根误差最终收敛时的最小值出现在截面尺寸为200 mm×300 mm时，此时的均方根误差约为0.008 52。说明在改变截面尺寸，即同时改变四个结构参数时，神经网络算法预测RC柱的预测结果仍具有较好的精度。所构造的神经网络在预测不同截面尺寸下的恢复力时体现出良好的泛化性能。

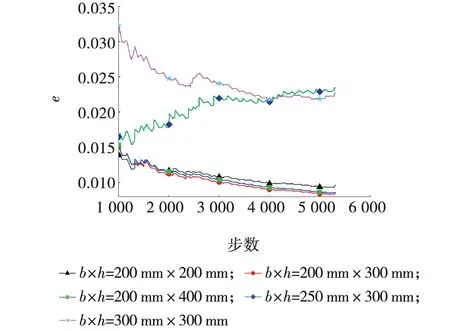
图12 不同截面尺寸时误差对比Fig. 12 Error comparison of different section sizes

由以上分析可知，以上预测结果虽然存在误差，但数据误差都很小，只有零点零几，甚至更小。因此，总体上恢复力的预测效果较好，精度较高。并且神经网络对不同结构参数下的恢复力的预测均具有良好的泛化性能。同时，考虑不同长细比时预测耗时约为14.79 s，考虑不同纵筋配筋率时预测耗时约为10.06 s，考虑不同体积配箍率时预测耗时约为9.97 s，考虑不同轴压比时预测耗时约为9.06 s，考虑不同截面尺寸时预测耗时约为10.31 s。由此可见，该方法计算效率较高。

3 结束语

为了预测不同构件的恢复力，提出了基于泛化神经网络算法预测RC柱恢复力方法，通过对RC柱的模拟仿真，验证了方法的有效性。与仅能预测同种构件恢复力的神经网络算法预测恢复力方法相比，所提出的方法可以预测不同结构参数下构件的恢复力。该方法具有较高的精度和较高的计算效率以及良好的泛化性能。