镐型截齿截割煤岩载荷的区间识别模型与解算方法

任春平，刘若涵，徐 鹏

(1.黑龙江科技大学 机械工程学院， 哈尔滨 150022； 2.黑龙江科技大学 招生与就业工作处， 哈尔滨 150022； 3.黑龙江科技大学 安全工程学院， 哈尔滨 150022)

0 引 言

镐型截齿截割煤岩载荷除与截齿的结构参数和工作参数有关外，还受煤质参数、地质条件等不确定性参量的影响，导致建立的载荷识别正向模型与真实载荷存在着不确定性，若继续利用确定性的技术处理，则得不到真实的有效载荷。对于不确定性的表达方式可分为概率方法、模糊方法和区间方法[1-3]。由于概率方法和模糊方法受条件的限制，较难获取有效的识别载荷[4-6]。对于截齿截割煤岩载荷这类工程问题，通常获取其边界应该是很容易的。

国内外学者在基于区间分析方法的载荷识别问题研究中取得了一些成果。Ahmari 等[7]采用区间分析方法，给出了煤岩参数的识别模型，有效识别其参数边界。Jiang等[8]建立了一种可以预测系统弹簧系数及质量范围的区间反演模型。Lee等[9]基于区间分析方法建立了适用于模态参数型修正问题的区间反演模型。Li等[10]应用区间分析方法研究了含有不确定参数的复合材料层合板材料参数识别问题，提出了一种用于不确定结构反演问题的区间方法。Au等[11]采用区间分析结合格林函数的技术，在时域中得到了待识别动载荷的区间估计界值。

区间理论分析方法对于不同研究对象其反演效果不同，没有形成统一的理论模型。在采掘机械领域其区间理论方法还处于探索研究阶段，尤其对镐型截齿载荷边界识别的研究国内外报道较少，由于镐型截齿的排列形式不同，目前对镐型截齿截割煤岩载荷边界的研究还不够成熟和完善。因此，在上述研究载荷识别基础上，笔者深入探求截齿载荷边界蕴含的信息，对研究滚筒载荷识别具有一定的参考。

1 载荷边界识别区间模型的建立

当煤岩截割参数中存在不确定参量时，截割煤岩响应参数卷积分[12-13]：

(1)

式中：p(τ,λ)——重构载荷；

λ——n维不确定性参数的向量;

g(t-τ,λ)——核函数。

由于式(1)的解不在是单一的解，而是一个解集，常规确定性方法很难直接来求解这类问题。因此，基于区间数学理论，探索截割煤岩载荷识别一种新的尝试。

区间数被定义为一对有序的实数：

AI=[AL,AR]={A|AL≤A≤AR,A∈R},

式中，I、L、R——区间、区间上界、区间下界。

对于煤岩参数存在不确定性参量得到的截割载荷，采用λI对不确定向量λ建模：

λ∈λI=[λI,λR],

(2)

λI为一个区间值，截割煤岩载荷也是一个区间值：

p(t,λ)∈pI(t)=[pL(t),pL(t)],

式中：pI(t)、pL(t)、pR(t)——时刻t的随机载荷区间、区间下界、区间上界。

根据区间数学理论，式(3)可以表示为

λI=[λI,λR],

λI=[λc-λw,λc+λw]=λc+[-1,1]λw,

(3)

式中，λc、λw——区间的中点和半径，

区间λI的不确定性水平被定义为

根据式(1)、(3)，不确定向量λ可以描述为

λ=λc+δλ,

对中点λw处进行一阶Taylor展开：

式中：p(t,λc)——区间中点值处的识别载荷；

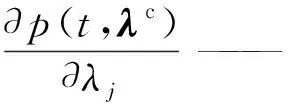
根据上述描述得：

p(t,λ)=p(t,λc+δλ)≈p(t,λc)+

(4)

因此，从式(4)计算得随机载荷识别区间模型，即载荷识别的上下界：

(5)

(6)

从式(5)、(6)可知，截割煤岩载荷边界不确定性识别可间接变成由确定性载荷进行识别。

2 区间模型解算方法

考虑噪声的影响，式(1)可以统一表达为

Ye=GPt+err，

将核函数矩阵G开展奇异值分解(SVD)，得

(7)

式中：U、V——由左奇异向量和右奇异向量构成的列正交矩阵；

∑——矩阵G的奇异值所构造的对角矩阵，∑=diag(σ1,σ2,…,σn)且σ1≥σ2≥…≥σn≥0。

因此，被识别载荷可以表示为

(8)

应用Tikhonov算法，可以得

(GTG+α2I)P=GTYerr，

式中，α——正则参数，可通过GCV或者L曲线方法获得。

结合式(7)、(8)得

利用上述方法求得不确定性参量中点值处的随机载荷p(t,λc)，而采用有限差分方法来计算不确定性参量的一阶偏导，这样识别两种确定性问题后，通过式(5)、(6)就可以识别最终的随机载荷的上下界。

3 应用算例

3.1 实验条件

利用自主研发的多截齿参数可调式旋转截割实验系统，开展煤岩截割测试研究，如图1所示[14-15]。实验条件：镐型截齿排列形式为棋盘式，截齿安装角为40°，轴向倾斜角为10°，二次旋转角为0°，最大切削厚度为20 mm，截割臂转速为40.8 r/min，牵引速度为0.82 m/min。测试得到的截齿轴向载荷如图2所示[11]。

图1 实验系统Fig. 1 Experimental system

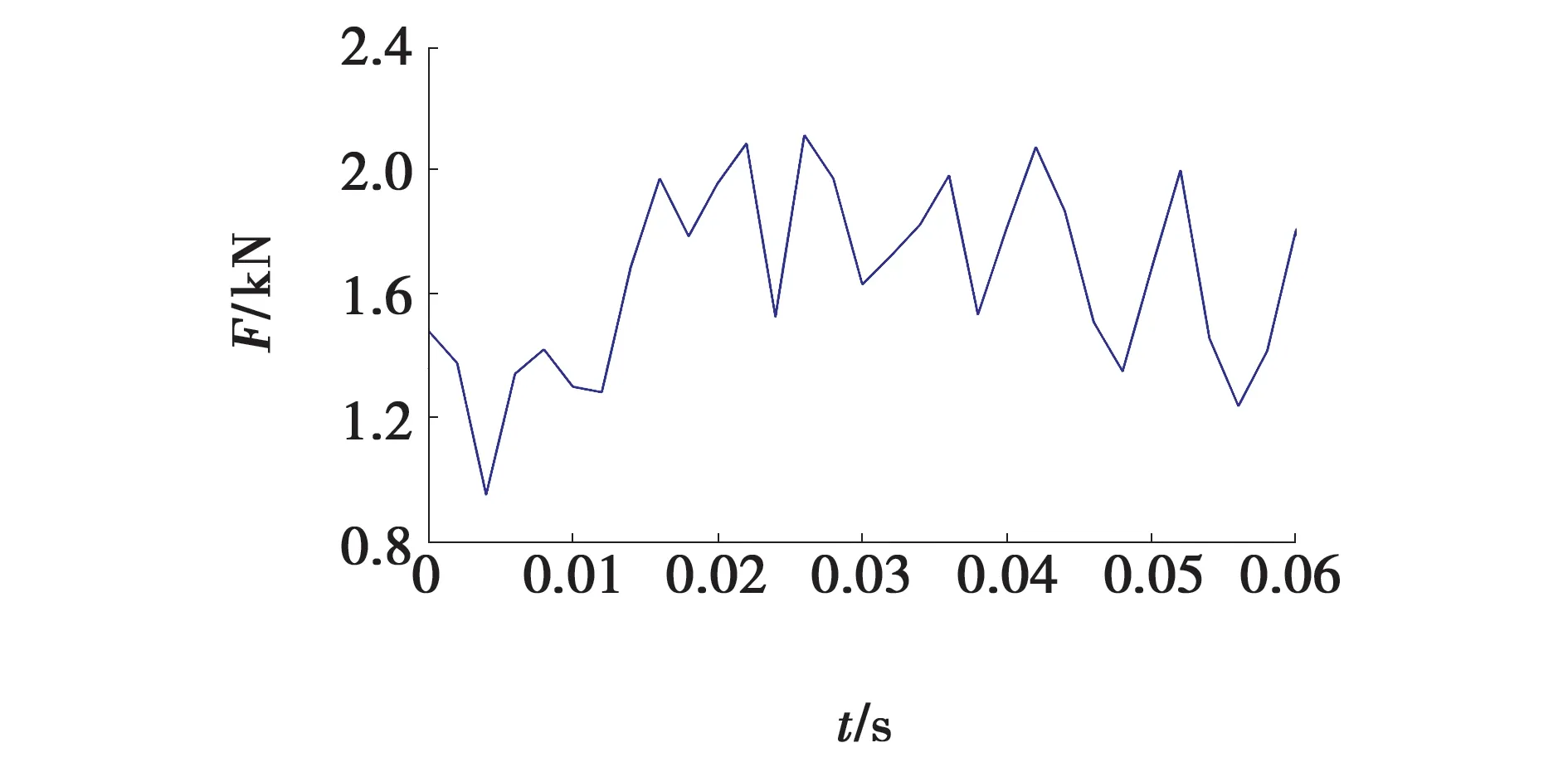
图2 截割载荷Fig. 2 Cutting load

3.2 识别结果

由于煤岩成因复杂，煤岩介质不均，呈各向异性，导致其煤岩密度的不确定性。因此，煤岩密度被视为不确定性参量，其中点值取为1 g/cm3，取2%、5%、7%、10%等不确定性水平，如表1所示。此外，为了有效地识别截割煤岩载荷边界，给出其评价指标：

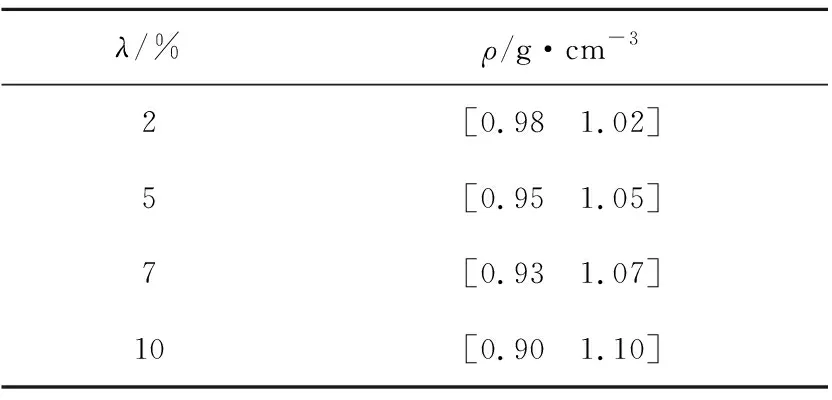
表1 不确定性参量的区间范围

首先，取不确定性参量的中点值，运用正则化载荷识别理论和方法，识别出参量中点处的截割载荷，如图3所示。

采用中心差分法，给出不确定性参量煤岩密度的敏感性曲线，如图4所示，其中η=∂p/∂ρ。

图3 区间中点处载荷识别曲线Fig. 3 Load identification curve at midpoint of interval

图4 载荷关于煤岩密度的敏感曲线Fig. 4 Sensitivity curve of load on coal rock density

在不确定性水平为2%、5%、7%、10%条件下，得到截割载荷边界的识别结果，如图5所示。从图5可知，截割煤岩载荷识别边界随着不确定水平的增大而增大。由图5a、b可见，在5%不确定性水平以内，区间分析法的识别结果都包含了实际的截割煤岩载荷。因此，采用区间分析法进行识别煤岩截割载荷边界中，在小不确定性水平条件下，可提高截割煤岩载荷边界的精度。

由图5c、d可见，在5%不确定性水平以上，载荷区间上下界随着不确定性水平的增加而扩张得比较越来越大。为了进一步评价不同不确定水平的载荷识别效果，给出了评价指标值，如表2所示。

表2 载荷识别评价指标

从表2可以看出，在2% 和 5% 的不确定性水平时，区间识别算法的识别截割载荷指标值分别为0.481 5和0.666 5。而在5%以上的不确定性时，当不确定性水平增大时，评价指标值也随之增大，尤其当不确定性水平为10%时，截割煤岩载荷边界识别结果远远偏离实际结果。

图5 不同不确定性水平的载荷识别结果 Fig. 5 Load identification results at different levels of uncertainty

综上所述，截割载荷在不确定性水平2%时识别载荷效果达到90%的理想程度。即能够充分说明区间理论分析法，在低不确定性水平时，其具有较好的识别效果和识别效率提高85%。同时，为研究滚筒载荷识别提供了理论参考依据。

4 结 论

(1)建立了截割煤岩载荷边界识别数学模型。将待识别煤岩截割载荷参量以区间描述和定量化，利用一阶Taylor的区间分析方法，将截割煤岩载荷识别转化为不确定参量中点处及其梯度识别的两类确定性问题。

(2)在2%和5%的不确定性水平时，所提出方法识别煤岩截割载荷指标值分别为0.481和0.666。而在5%以上的不确定性时，指标值随着不确定性水平的增加而增大，当不确定性水平为7%和10%时，与2%的指标值相差二倍。因此，在2%的不确定性水平时，煤岩截割载荷边界识别效果相对较理想。