一种柔性空间双臂机器人的协同控制和避障方法*

冯 钧，孔建寿，王 刚

0 引 言

近年来，随着航天事业的迅速发展和空间探索技术的深入，空间机器人在空间探索领域发挥着越来越重要的作用,对空间机器人的研究日渐受到学者们的重视.同时，随着仿生学和机器视觉的进展，越来越多的专家和学者注意到生物的柔性和灵活性，提出了柔性空间机器人的概念，使其成为未来机器人领域的一个新兴的研究分支.

柔性空间机器人因其具有高灵活性、可变形性和能量吸收性、较强的环境适应性等特点，使其在一些诸如大型空间站的在轨组装、搬运物体、姿态管理、辅助对接和装配工序等复杂的空间应用越来越频繁.因此，柔性空间机器人的运动学、动力学及控制问题研究具有重要的理论意义和实际价值.

目前，双臂空间机器人比单臂空间机器人具有更大的负载能力，更好的运动稳定性以及更高的灵活性，因此，关于双臂空间机器人的协同控制的研究引起越来越多学者的兴趣[1-5].

徐文福[6]等研究了双臂空间捕获目标的自主路径规划问题，提出了基座自由漂浮和姿态受控2种情况下的自主路径规划方法.洪昭斌[7]等研究了开链双臂空间机器人系统的自学习控制.王从庆[8]等研究了载体位置、姿态均不受控情况下闭链双臂空间机器人系统的鲁棒协调控制问题.Shan[9]等研究了双臂空间机器人捕获卫星过程中无反作用的最优路径规划策略.程靖[10]等研究了基于双臂机器人空间机器人系统的自适应模糊控制方案，但仅考虑了关节角及姿态镇定控制问题.

本文对空间双臂机器人协同控制的运动学问题展开研究，通过引入绝对位姿变量和相对位姿变量，获得对协同控制任务在运动学层面上的直观表述，并在此基础上进一步提出一种新的基于自运动特性的柔性空间双臂机器人协同控制和避障任务调度算法，有效解决在搬运任务执行过程中可能发生的机械双臂与其它物体之间的碰撞和接触问题，最后通过仿真试验和样机模拟验证算法的可靠性和有效性.

1 柔性空间机器人耦合动力学模型

在对双臂机械手协同操作任务的描述中，采用面向任务的控制方式，通过引入表示空间中的目标实际运动情况的绝对位姿和用于表示两个机械臂之间相对运动的相对位姿两个概念，来分析柔性空间双臂机器人的运动学特征[7].

1.1 空间绝对位姿

对于由两个机械臂组成的协同控制系统，以其中任意一机械臂为分析对象，令xi(i=1,2)表示该机械臂的末端位置向量，Ri(i=1,2)表示该机械臂的末端坐标的姿态矩阵.机械臂末端的角速度向量ωi(i=1,2)和姿态矩阵Ri(i=1,2)存在如下关系：

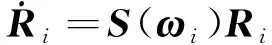
(1)

为了实现对协同控制任务的运动学描述，首先通过一组变量来指定控制目标在空间中的实际位姿.位置由固连在操作目标上的绝对坐标系的原点表示，设该点在基坐标系中的位置坐标为xa，则

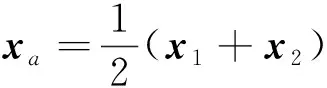
(2)

式(2)中，x1,x2分别表示双机械臂的末端坐标位置向量.如图1所示.

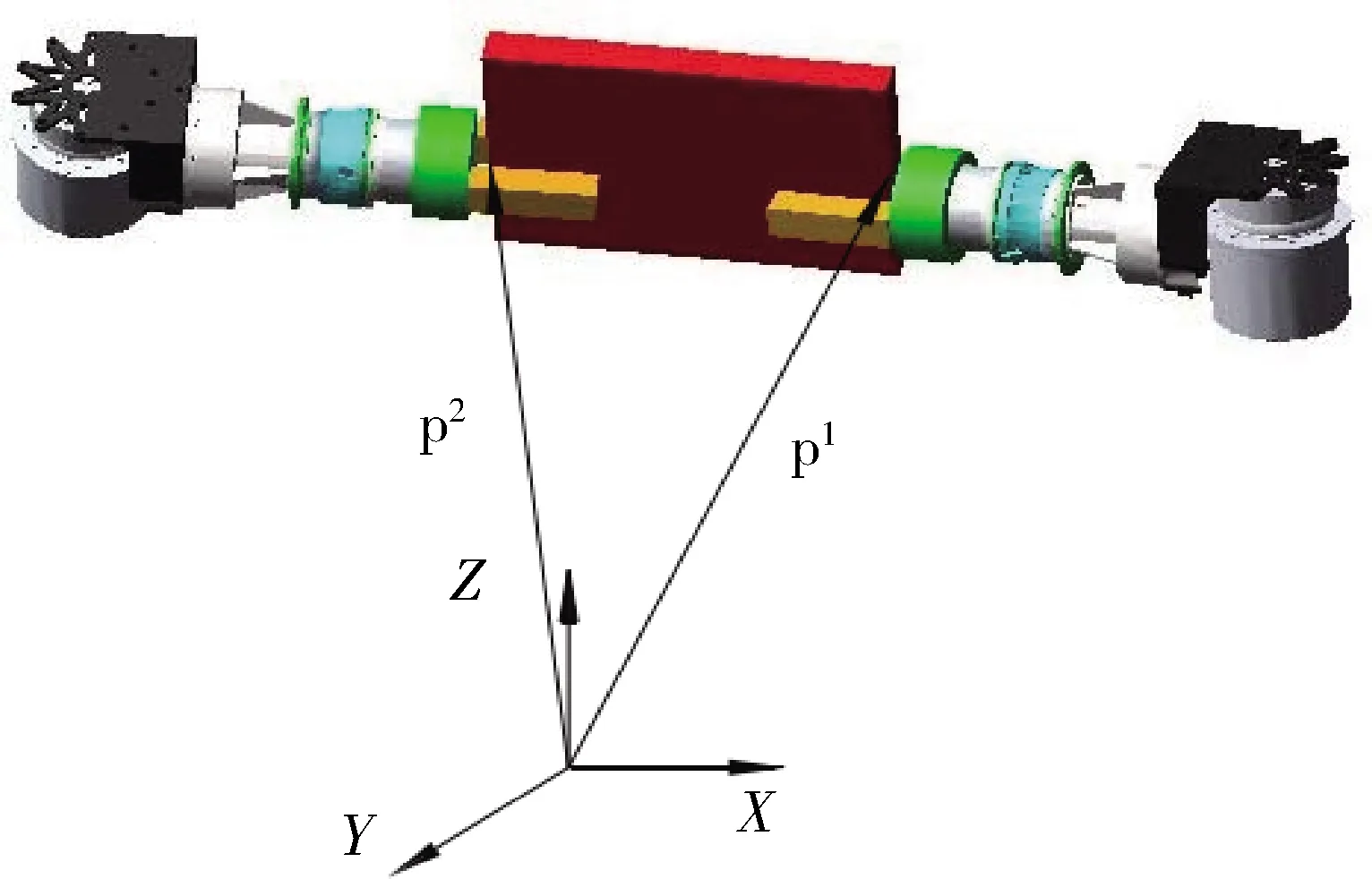
图1 机器人双臂末端图Fig.1 Schematic of double-arm cooperative system

为了有效表示控制目标在工作空间中的绝对位姿，引入矩阵算子Rk(v)的概念，用以表示以单位向量k为轴线转动角度v，则固定在操作目标上的绝对坐标系相对于基坐标系的姿态旋转矩阵可以表示为

(3)

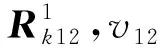
由式(2)对时间求导，可以得到绝对线速度

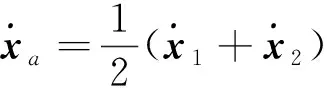
(4)

由式(3)对时间求导，可以得到绝对角速度

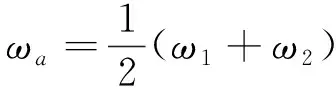
(5)

式(5)中，ωi(i=1,2)分别表示双机械臂的终端相对于基坐标系的角速度向量.

1.2 空间相对位姿

绝对位姿变量通过双机械臂的终端位姿的组合实现了对控制目标的运行状况的描述，但仅凭绝对位姿变量无法实现对整个协同控制的具体描述.在对协同控制和操作任务进行描述的过程中，还须考虑双机械臂之间的相对位置，因而再引入相对位姿变量来对双机械臂的协同控制情形进行描述.

双机械臂末端之间的相对位置即为

xr=x2-x1

(6)

双机械臂终端之间的相对姿态可以定义为双机械臂终端之间的相对旋转矩阵，即

(7)

由式(6)对时间求导，可得到相对线速度

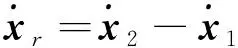
(8)

由式(7)对时间求导，并结合式(1)，可得到

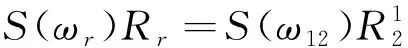
(9)

可得到相对角速度

ωr=ω2-ω1

(10)

1.3 运动学方程

不失一般性，考虑双臂空间机器人单机械手终端速度和关节速度间的关系为

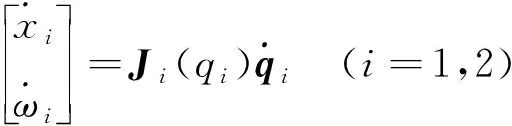
(11)

其中，J,q分别表示机械手的Jacobian矩阵和关节速度向量.

根据式(11)，结合式(4)、(5)得到

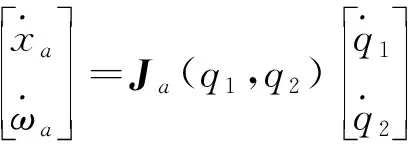
(12)

同理，结合式(8)、(10)可以得到

(13)

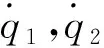
通过以上步骤，结合式(12)、(13)，得到空间双臂机器人系统整体动力学方程

(14)

其中：

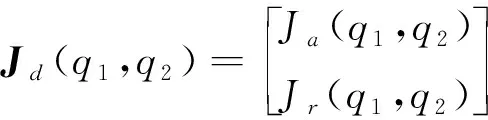
(15)

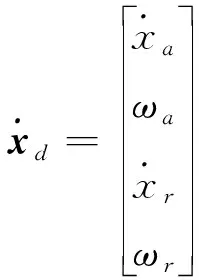
(16)

(17)

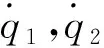
1.4 刚柔耦合系统动力学模型

采用多体动力学软件ADAMS建立柔性机械臂的动力学模型，基于拉格朗日法和假设模态法，机械臂的刚柔耦合动力学模型描述如下：

(18)

2 空间双臂机器人协同控制和避障任务调度算法

柔性空间双臂机器人的协调操作规划中，也存在着为了保障工作人员和机器人系统的安全而必须考虑的避障问题.基于目前已被广泛使用的最小距离的单臂冗余度机器人避障算法的基本原理[8]，本文提出柔性双臂机器人的协调控制和避障算法，使得冗余双臂机器人的能够同时完成末端的协调操作和避障任务.

2.1 柔性空间机器人的运动学逆解

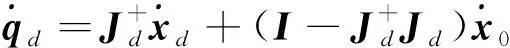
(19)

2.2 拟运动学解空间

柔性空间双臂机器人的协同控制和避障是通过双机械臂上的传感装置来持续地检测障碍物的位置信息，当发现障碍物和双机械臂之间的最小距离小于设定阈值时，开启避障功能.该方法的原理就是设定一个最小距离，并定义双机械臂上最靠近障碍的点为关键点.避障就是通过运动学求解，得到一个使关键点远离障碍的避障速度向量.

设di0为障碍上最近点指向机械臂i上的关键点的向量，其对应单位向量为

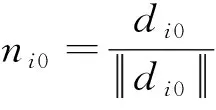
(20)

则关键点运动Jacobian矩阵为

(21)

其中：J0为关键点空间运动Jacobian矩阵.

2.3 柔性空间机器人双臂协同控制和避障任务调度算法

柔性空间双臂机器人的协同控制和避障规划问题，要求在机械臂执行任务时，既不与障碍发生碰撞的同时，又能够完成双机械臂终的协同控制任务.为了有效解决柔性空间机器人逆运动学解运算量大、实时性差的特点，可在式(14)的基础上，通过将逆运动学解空间看作一个光滑流形，对位置工作空间流形和自讨工作空间流形分别进行降维，通过算法改进得到新的面向柔性空间双臂机器人的相应优化逆解为

(22)

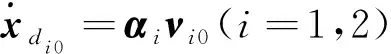
(23)

式(23)中：νi0为给定的关键点的避障速度初始值，αi为避障增益

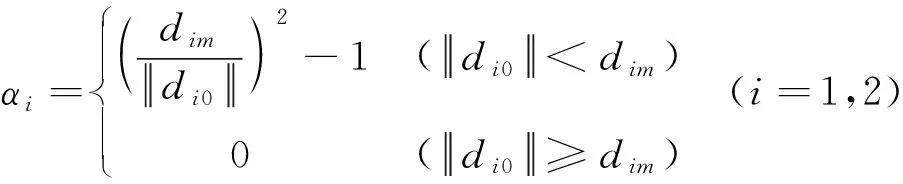
(24)

关节速度和关节角速度的关系为

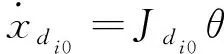
(25)

综上所述，由于双机械臂的控制行为运动都仅仅在零空间上进行，故不会对协同控制任务造成影响.因而可运用该算法同时实现双臂机器人的协同控制和避障规划.

3 仿真实验

3.1 仿真环境

为了验证本文提出的协同控制和避障算法的可行性，下面以某空间双臂机器人作为研究对象进行仿真试验，如图2所示.

图2 柔性空间双臂机器人Fig.2 Flexible space dual-arm robot

该机器人由高度模拟化的双机械臂组成，每个机械臂由七个旋转关节串接而成，如图3所示.

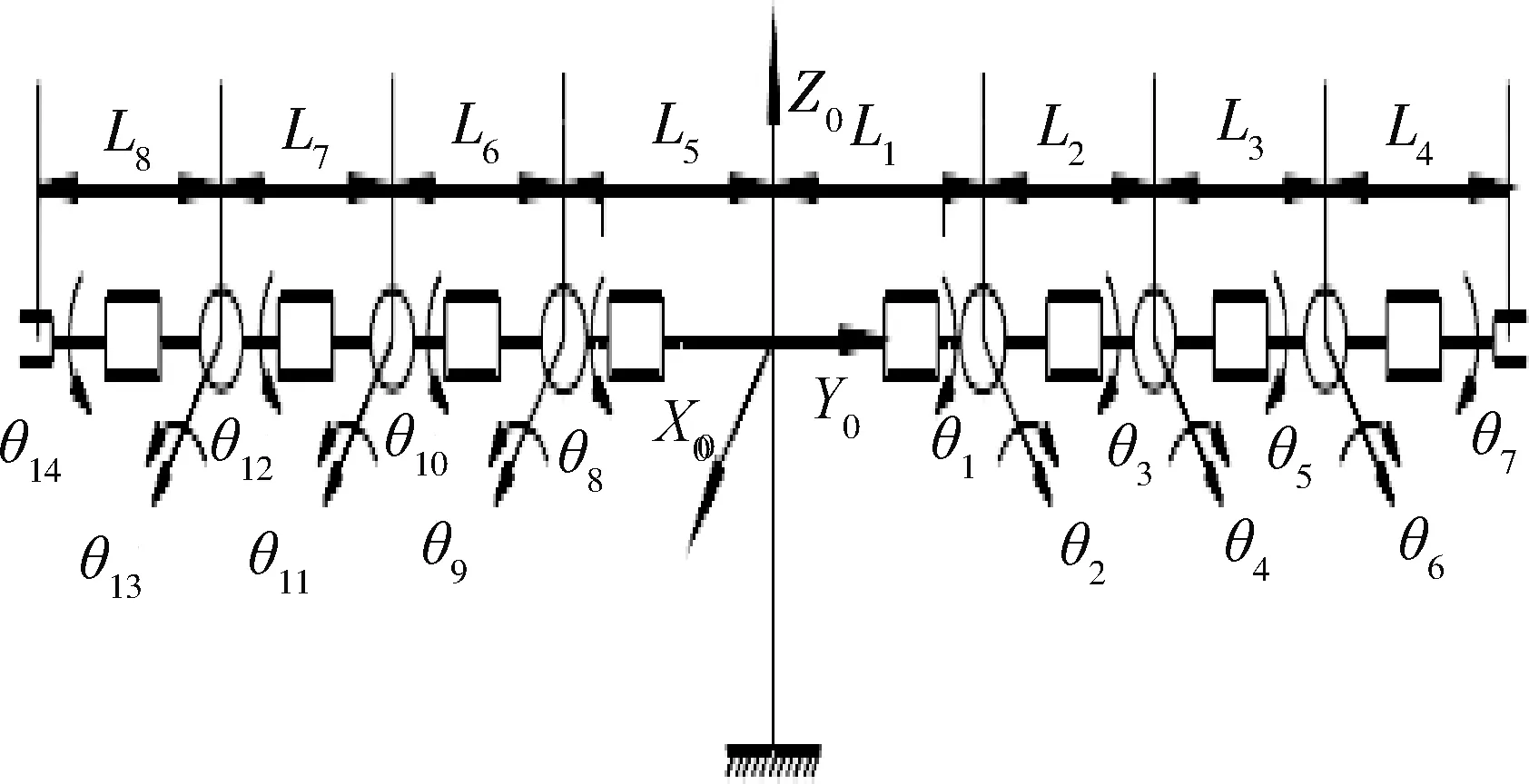
图3 结构图Fig.3 Diagram of mechanism

仿真试验在RecurDyn V7R5的软件环境下进行，验证柔性空间双臂机器人在有障碍物的工作环境中是否能够顺利完成协同抓取任务.协同控制任务的过程为两个机械臂共同抓取一物体并将它从初始位姿移动到指定的目标位置.

仿真参数设定：机器人各构件长度为L1=L5=0.49 m,L2=L6=0.317 m，L3=L7=0.304 m,L4=L8=0.311 m，工件长度为0.38 m；初始关节角分别为：

左臂、右臂的初始末端位置分别为(0,-0.19,0.31)，(0,0.19,0.31)，左臂和右臂相对于基坐标系的初始姿态旋转矩阵分别为

仿真时间设置为2 s.在空间中存在两个半径是0.05 m的绿色球体，其球心位置为(-0.021,-0.52,0.24)、(0.047,0.63,0.27).

图4 起始状态Fig.4 Initial state

3.2 仿真结果

柔性双臂机器人运动情况与障碍位置关系如图5所示.从图中可看出，机械双臂预期可完成任务，但会与绿球发生碰撞.

图5 算法实施前机器人运动轨迹Fig.5 Traces of robot before the implementation of the algorithm

采用式(21)所描述的算法后机器人的运动情况如图6所示.从图6中可以看出，双臂灵活地避免了与障碍物之间的碰撞，并较好地实现了协同控制任务.

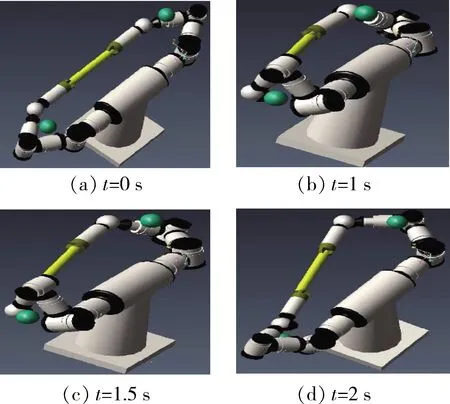
图6 算法实施后机器人运动轨迹Fig.6 Traces of robot after the implementation of the algorithm

图7 最小距离Fig.7 Minimum distance

图8、9分别标明了机械双臂关节角度变化曲线连续、平滑、表明关节运动平稳.

图8 左臂关节柔性变化轨迹图Fig.8 Flexibility change trajectory diagram of left arm joint

图9 右臂关节柔性变化轨迹图Fig.9 Flexibility change trajectory diagram of right arm joint

4 面向搬运任务的样机试验

4.1 虚拟样机系统的构建

根据相对位置关系将各关节组装成装配体，基于三维建模软件SolidWorks建立机器人双臂各关节、腰部和L型关节连接件的立体CAD模型，如图10所示.

图10 空间机器人系统立体模型Fig.10 Three-dimensional model of space robot system

4.2 双臂协调搬运任务的仿真实验

空间双机械臂在相同时刻协同抓取并搬运物体的工作流程图如图11所示.

图11 协同搬运工作流程图Fig.11 Flowchart of coordination handing

搬运任务属于紧协调任务，最主要的部分是基于提出的反向运动学模型进行计算，需要根据左右臂之间严格的约束条件规划好它们的运动轨迹.通过冗余机器人双臂协调控制，可以完成协调搬运任务，如图12所示.

图12 协同搬运任务试验Fig.12 Test of coordination handing task

在协同搬运任务试验中双臂各关节变化曲线如图13和图14所示.

图13 左臂各关节柔性变化轨迹图Fig.13 Flexibility change trajectory diagram of the left arm joints

图14 右臂各关节柔性变化轨迹图Fig.14 Flexibility change trajectory diagram of the right arm joints

图13和14中前10 s双臂关节均为均匀运动，10 s后是机械双臂抓取并搬运空间物体的关节角度变化轨迹，在20～30 s则是双臂分别复位的关节角度变化轨迹.从图中可以看出，各关节转角均未突破关节运动极限，从而可以有效实现空间协同搬运任务.

5 结 论

本文针对柔性空间双臂机器人系统的协同控制和避障规划问题，提出了空间位姿变量来描述协同控制并完成空间在轨搬运任务的方法.仿真试验表明该方法在保证空间双机械臂能够顺利完成协同搬运控制任务的同时，可顺利实现避开空间障碍物.