柔性铰接板振动测量及迭代学习主动控制*
邱志成,黄子骞
0 引 言
大型柔性板状结构广泛应用于航空航天领域,但这种结构特性极易引起低频振动[1].从动力学角度分析,大型柔性结构通常具有柔性大、低频模态密集、模态耦合度高等特点[2],故而采用传统的控制方式或单一形式的被动控制方式难以实现预期的振动抑制效果.与被动控制方式相比,主动控制能更好地适应工作环境、具备更优的灵活性,使用主动控制方式对柔性结构的振动进行抑制是一种行之有效的方法.基于此,探讨大型柔性结构如太阳翼、薄膜天线等板状结构的主动控制具有一定的研究价值和研究意义.
关于振动控制,CHU等[3]针对双连杆柔性机械臂研究了一种基于输入整形器和多模态自适应正位置反馈的振动主动抑制方法,实验结果表明了该方法具有可行性和适用性.EHSAN等[4]提出了一种新型MPF控制器用于压电柔性结构的振动主动控制,并采用H2和H∞范数对增益进行优化,实验结果表明相较于MPPF控制器,MPF控制器不仅能有效地抑制振动位移和速度,而且具有更好的性能.HUANG等[5]针对超长柔性机械臂在冲击载荷作用下的端部振动问题,提出了一种改进的最小均方法来确定控制路径的频域响应矩阵和外部激励响应的复振幅,实验结果表明所提出的方法能有效降低机械臂的振动幅值.NATRAJ等[6]采用了一种混合控制技术以探究双连杆柔性机械臂的振动主动控制问题,这一技术涉及到压电陶瓷传感器和驱动器的组合使用,为本文研究柔性结构的振动测量装置及主动控制装置提供了参考.MOSTAFA等[7]对多连杆柔性机构的建模与控制研究的发展趋势进行了综述,包括FLMs的建模方法和实现的控制技术等内容,趋势表明,开环控制、前馈控制等策略已被频繁地用于连杆柔性机构的振动主动控制.
在研究柔性结构的振动检测与振动主动控制过程中,振动检测装置及方法、振动控制装置及方法在选用和实施上有着举足轻重的重要性.压电陶瓷是一类具有压电特性的电子陶瓷材料,因其材料特性故而在机械应力的作用下将引起压电陶瓷内部正负电荷中心的相对位移从而形成极化现象,导致材料两端表面分布集结了符号相反的电荷即压电效应.压电陶瓷成本较低、易于安装,OLIVER等[8]利用压电材料研究了轴流中平板颤振时产生的能量;HE等[9]在经典层合板理论的基础上,研究了基于压电传感器和执行机构的功能梯度材料板的主动振动控制.本实验将选用压电陶瓷传感器作为柔性板的主要振动检测装置.
在柔性结构振动主动控制的研究中,主动控制算法的选用将直接决定控制效果的优劣.主动控制包括经典的PID控制、现代控制、智能控制[10]等.迭代学习控制(ILC, iterative learning control)就是一种典型的智能控制,该方法于1984年由Arimoto等[11]提出,而后一直发展成智能控制系统中具有严格数学描述的一个分支.如果要求系统在有限的时间间隔t⊂[0,T]内准确地完成给定的跟踪任务,传统的控制手段可能无法实现控制目标,但采用迭代学习控制的方法是可以满足这一控制要求的,条件是给定的任务能够重复一定次数,且最初几次基于迭代学习控制的误差在可接受的范围内,此外重复执行过程中的跟踪误差、输入和其他需要的信号是能够被测量和存储的[12].曹树平等[13]将迭代学习控制方法应用于一类电液位置伺服系统,实验结果表明只要选择合适的学习律就能对系统实现有效控制.CHIEN等[14]针对一类非线性系统提出了一种模型参考迭代学习方法,与传统的迭代学习控制方法相比,模型参考的迭代学习方法可以更灵活地适用于多种情形下的轨迹跟踪,通过在工业机械手上的成功应用验证了该方法的可行性.孙瑜等[15]给出了一类非线性时变系统在任意初值条件下采用开环D型迭代学习控制算法时的收敛条件,该算法克服了系统输出信号跟踪期望输出依赖于期望状态和期望输入的缺陷,解决了迭代学习控制中的初始状态问题,仿真研究结果表明该算法具有可行性.
本文以柔性板状结构的振动测量和主动控制为研究目的,以柔性铰接板为研究对象,为此搭建了一套用于测控柔性铰接板振动特性的实验平台;而后将压电陶瓷传感器粘贴于柔性板表面,用于检测待测对象的振动信息;根据系统结构特性分别设计了迭代学习控制器和PD控制器,通过实验比较两者的控制效果,以此验证所研究的控制方法的可行性和优越性.
1 实验系统
图1(a)所示为本文的实验系统示意图,主要研究柔性铰接板的振动测量及主动控制,它由以下这几个部分组成:柔性铰接板主体、双目视觉检测系统、压电陶瓷传感器、信号转换及放大模块、运动控制卡、计算机、压电陶瓷驱动器等.
柔性铰接板是本实验系统的研究对象,如图1(b)所示为柔性铰接板的平面示意图,它由两块柔性板通过上下两个弹簧铰链铰接形成一个整体,并由机械支撑架夹持装置固定在水平基座上.其中,柔性板I的尺寸为560 mm×510 mm×2 mm,柔性板II的尺寸为300 mm×510 mm×2 mm.它们均使用环氧树脂材料制成,其弹性模量E0=24 GPa,泊松比μ=0.33,密度ρ=2141 kg/m3.整体而言,柔性铰接板一端通过夹持形成固定端,另一端不加约束即为自由端,整个柔性铰接板主体呈现为一悬臂结构.所述两块柔性板的长宽尺寸均为板厚的100倍以上,符合克希霍夫薄板理论,即当柔性板承受横向载荷时会发生弹性形变,在柔性板横截面上各点沿横向产生的位移称为挠度.对于一阶弯曲振动模态,从材料力学角度来看,从悬臂端到自由端,柔性铰接板在横向方向的挠度是逐渐增大的,而纵向方向形变程度是一致的.因此在研究柔性铰接板的振动测量方法和振动控制方法时,可依据柔性铰接板的结构特性合理地布置传感器和驱动器.

图1 实验系统及柔性铰接板示意图Fig. 1 Schematic diagrams of the experimental system and the flexible hinged plate
在图1(b)中,可见在柔性板I和柔性板II表面均粘贴有数个标志点,它们可组成一个完备的标志点序列用于柔性铰接板的形态可视化研究,这在后续实验中将会有深入探究.本实验仅选用最靠近自由端那一列的标志点1~标志点5(P1~P5)用于视觉振动测量,其检测原理简述如下:双目视觉测量基于视差原理,可采用张氏标定法对所配置的双目视觉系统进行相机标定,之后双目视觉系统采集柔性铰接板振动状态下的图像,采集到的图像经图像处理及特征点立体匹配等步骤后可得到图像中标志点的三维坐标信息.如图1(a)中的信号流1表征了双目视觉测量方式的信号流向.鉴于相机标定及三维解算的方法已相当成熟,此处不再赘述,详尽可参考文献[16].至此在柔性铰接板的振动过程中,某一时刻板上标志点的振动位移量可表示为
(i=1,…,5)
(1)

最后,对于柔性铰接板的一阶弯曲振动,将标志点1~标志点5的振动位移量作算术平均即可得到视觉测量下柔性铰接板的一阶弯曲振动量dv,即

(2)
在图1(b)中,可见在柔性板II上粘贴有数个压电陶瓷片,单片尺寸为50 mm×15 mm×1 mm.其中片9是压电陶瓷传感器,它粘贴在柔性板II的中线附近且靠近固定端根部位置,主要用于检测柔性铰接板的一阶弯曲振动,其检测原理如下:在振动过程中,粘贴在柔性板固定端处的压电陶瓷传感器因柔性板的变形而随之发生形变,根据压电效应,当压电陶瓷传感器发生形变时,它的两个相对表面上会分别聚集极性相反的电荷,故而在压电陶瓷内部形成了电势差.将压电陶瓷传感器表面电荷信号通过电荷放大器放大,再由端子板进行A/D转换,可得到压电片当前形变量的数字表达形式,如图1(a)中的信号流2表征了压电测量方式的信号流向.在实验的初始化配置时,反复调节电荷放大器的放大倍数,并对比同一时刻下视觉检测的信号和压电检测的信号,最终得到基于压电的检测方式其测量范围在(-6 V,6 V)时对应的柔性铰接板末端实际横向位移范围为(-10 mm,10 mm),即压电检测方式的灵敏度为sps=600 mV/mm.在这个幅值振动范围,二者之间近似满足线性关系,即压电测量下柔性铰接板的一阶弯曲振动量dps可表示为

(3)
式中,ups为压电测量的电压值大小.
在图1(b)中,片1-8均为压电陶瓷驱动器,它们对称粘贴在柔性板靠近固定端根部位置的前后两面,每面4片且并联连接,主要用于抑制柔性铰接板的一阶弯曲振动,其控制机理如下:计算机根据检测装置反馈的振动量输出指令到运动控制卡上,后者输出控制信号,而后经端子板上D/A转换得到模拟信号,信号再通过电压放大器放大,最后由压电陶瓷驱动器输出电势差.根据逆压电效应,当压电陶瓷两表面间有电势差时,驱动器上会产生力矩,从而抑制柔性板的振动.如图1(a)中的信号流3b表征了压电驱动方式的信号流向.在实际实验中,所设计的控制器输出的电压值范围在(-5 V,5 V),经转换放大52倍后由8片压电陶瓷片组合成一路压电驱动器输出,这种组合输出具体表征为:振动控制过程中,计算机输出a(-5 V≤a≤5 V)大小的控制指令,经转换放大后柔性板正面的4片压电陶瓷驱动器均输出52a(V)大小的电压,与此同时柔性板反面的4片压电陶瓷驱动器均输出-52a(V)大小的电压.对于柔性板上双面对称粘贴压电片单元(如下简称双晶片),在外加电压upa作用下,双晶片内部会产生一电场E,且正反两面压电片所受电场的大小相等,方向相反,致使某一面的压电片会伸长而另一面的压电片会收缩,从而驱动柔性板向一个方向弯曲.对单一双晶片而言,参考文献[17]可知,其产生的力矩:

(4)
式中,d31为压电片的压电应变常量,Ep为压电片的弹性模量,E0为柔性板的弹性模量,w为压电片宽度,h为压电片厚度,h0为柔性板厚度,upa为外加电压.如图1(b)所示为柔性板上8片压电片的配置方式,它们上下对称、前后同位,这种配置方式保证柔性铰接板在根部位置能受到足够的驱动力作用,同时也能保证柔性铰接板在根部上半面和下半面的受力均等,不至于因受力不均而激起板子其他模态的振动.实验结果表明所使用的压电陶瓷驱动器满足控制性能需求.
2 迭代学习控制器设计
假设被控对象的状态方程为

(5)
其中,x⊂Rn×1,y⊂Rm×1,u⊂Rr×1分别为状态向量、输出向量、输入向量,n,m,r表示维数,A,B,C为相应维数的矩阵且CB是非奇异矩阵.
图2所示为典型的迭代学习控制原理图,其中xk,yk,uk分别为系统第k次运行时系统的状态量、输出量和输入量,yd(t)是系统的期望输出,输出误差ek(t)=yd(t)-yk(t).此外,图2中的学习律是对控制量uk而言的,一般地,迭代学习的控制量都可用递推的形式来表示

图2 迭代学习控制原理图Fig.2 Schematic diagram of iterative learning control
uk+1(t)=L(uk(t),eλ(t))
(6)
其中,λ=k时表示开环迭代学习,λ=k+1 时表示闭环迭代学习.迭代学习控制的目的是,已知系统每次的初始状态xk(0)和期望输出yd(t),系统按照一定的学习律进行多次重复的学习,每次的学习时间为t⊂[0,T],要求k→∞,存在理想的控制量uk(t)使得系统的输出yk(t)→yd(t).当k→∞时,要求ek(t)在t⊂[0,T]上一致趋于0,则称该迭代学习控制是收敛的.只有当迭代学习过程是收敛的,这样的迭代学习才有实际应用意义.迭代学习控制理论适用于具有重复运动性质的被控系统,可实现有限区间上的完全跟踪任务,它用系统的实际输出信号与期望输出信号之间的误差作为参考,按照一定的规律进行学习以修正不理想的控制信号,从而使得整个系统的控制性能得到提升.本实验研究的是柔性铰接板在受到外部激励下的振动情形,具有重复运动的性质,比较适合于用迭代学习的方法进行控制.然而,目前大部分的迭代学习控制的研究都要求系统每次运行时的初始状态满足
xk(0)=xd(0),k=0, 1, 2,…
(7)

uk+1(t)=(1-g(t))uk(t)+g(t)u0(t)+

(8)
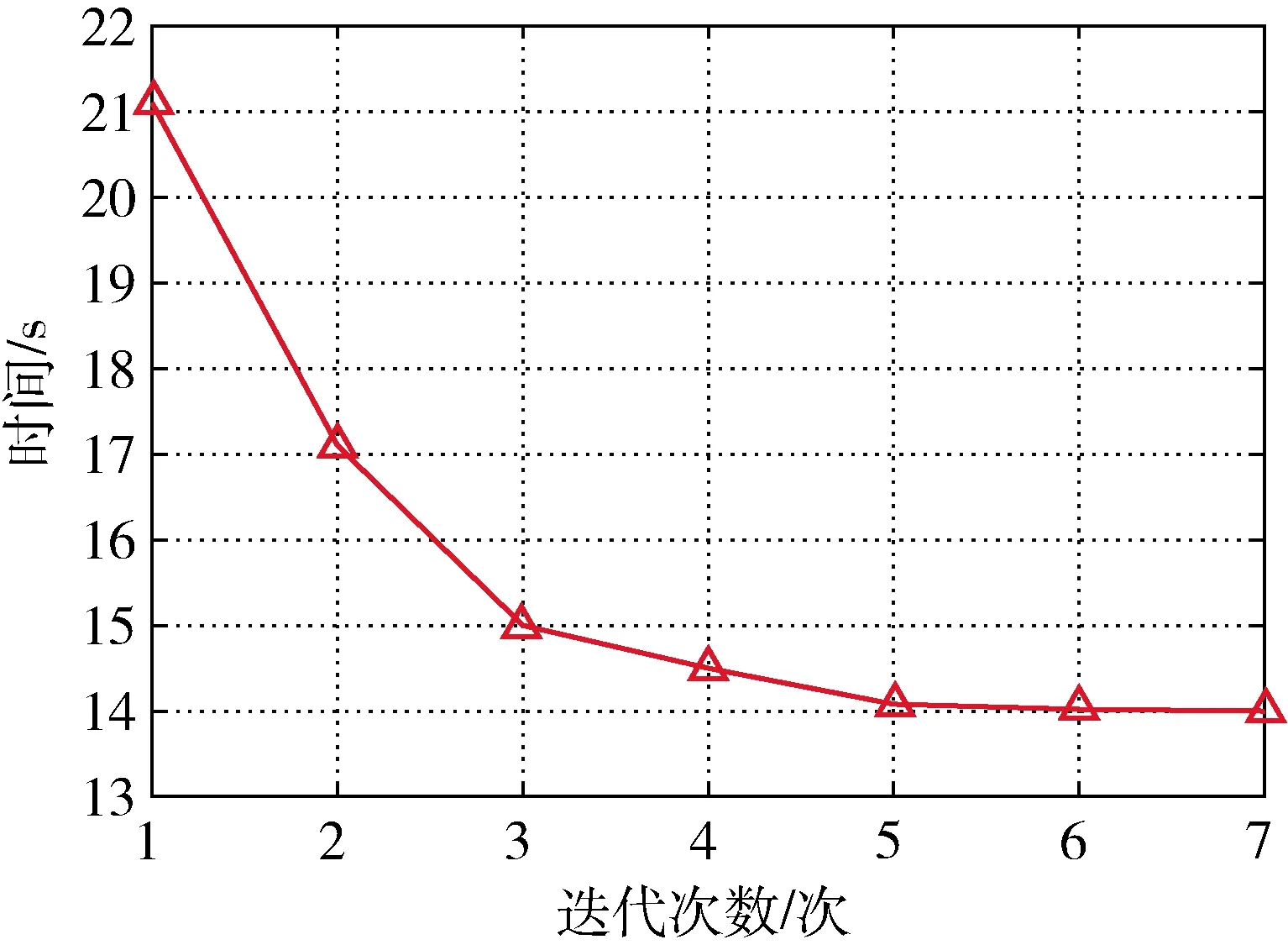
其中,g(t)是uk(t)的变遗忘因子函数,0 ∀x⊂Rn×1,t⊂[0,T] (9) (10) 其中,0≤a<1,b1 (11) 将式(11)代入式(8)中,则最终迭代学习控制的学习律为 (12) 如图3所示为本实验的实体装置图.本实验将重点研究柔性铰接板的一阶弯曲模态,为有效抑制振动,选用型号为GTS-400-PV-PCI的固高运动控制卡输出控制信号,经压电放大器后输出到压电驱动器.压电传感器检测的信号经放大、A/D转换、采样等操作后,换算得到实际可检测的最小应变单位为0.1 mm,压电陶瓷传感器检测的振动电压型号,折算到柔性铰接板末端振动的实际横向位移范围为(-10 mm,10 mm);相机图像传感器的分辨率为1920 Pixel×1200 Pixel,视觉方式检测的信号经图像处理、立体匹配等处理后,换算得到实际可检测的位移变化量单位为0.1mm,视觉方式检测的柔性铰接板末端振动实际横向位移范围在(-10 mm,10 mm),且相机所采集的信号仅作参考对比.所设计控制器输出的电压值范围在(-5 V,5 V),经电压放大器(芯片型号PA240CX)放大52倍后至(-260 V,260 V). 图3 实验平台实体装置图Fig. 3 Photos of experimental system 软件方面,在VS编程环境里使用C++语言编写控制算法及界面.考虑到视觉检测处理时间的需要,实验时,采样周期设定为50 Hz.进行柔性铰接板一阶弯曲模态的自由振动测试,并分别采用PD控制和迭代学习控制算法进行主动控制并探究其控制效果. (1) 自由振动实验结果 在柔性铰接板的悬臂端施加一激励使其产生振动,过程中不加入任何控制以使其保持自由振动状态,且同时采用视觉方式和压电传感方式检测柔性铰接板的振动.图4(a)为压电片所测dps-t表示的振动曲线,dps即压电测量下柔性铰接板的一阶弯曲振动量,是通过式(3)转换得来的,单位mm. 图4(b)为相机所测dv-t表示的振动曲线,dv即视觉测量下柔性铰接板的一阶弯曲振动量,是通过式(2)计算得来的,单位mm.图4(c)所示为压电片所测前30s振动曲线.对比发现,压电片所测信号曲线光滑稳定,噪声小;而相机所测信号曲线不够光滑,且在小幅值范围噪声影响较为明显,这些可能与相机的分辨率和光照等因素有关.可见相比于相机,选用压电片作检测得到的振动信号会更加稳定可靠,后续实验中的振动响应曲线均为压电片所测. 图4 自由振动时域响应Fig.4 Time domain response of free vibration 从图4(a)可知,柔性板的初始振幅在10±0.2 mm附近,在不加入任何控制作用下,柔性铰接板会持续振动65 s左右才衰减到2%,即进入小幅值范围;到90 s左右衰减到0.5%以内,此时柔性铰接板基本趋于稳定状态.此外,从图4(a)可见系统存在由噪声引起的零漂现象,接下来便从频域角度分析并解决这一问题.图5(a)所示,为自由振动时域曲线所对应的功率谱密度图,从图上可知,系统在1.15 Hz时达到峰值11.67 dB,为系统的一阶弯曲模态频率.但在低频段存在-5 dB到-10 dB不等的低频噪声对系统的干扰;在6.575 Hz处出现另一极大值,这是系统的第二阶弯曲模态频率.本实验重点研究柔性铰接板一阶弯曲模态的振动情况,故而应尽量避免二阶及以上振动模态的影响.因此,针对这一现象,使用巴特沃斯带通滤波器对信号进行滤波处理.如图5(b)所示,为滤波后的功率谱密度图.从图上可见滤波后,0.5 Hz及以下低频段的信号,幅值均不大于-20 dB,改善了低频段对系统的影响;在5 Hz及以上频段的信号,幅值较之前均下降了近20 dB,减少了高频段对振动信号的干扰. 图5 自由振动频域响应Fig. 5 Frequency domain response of free vibration (2) PD控制实验结果 图6为柔性铰接板的PD控制实验结果,PD控制器的控制参数分别是kp=0.86,kd=0.02,控制量向后移20个采样周期后开始控制.对比图4(a)和图6(a),柔性板的初始振幅都在10±0.2 mm附近,相比于自由振动,PD控制下柔性板会在21 s左右衰减到2%的小幅值范围,可见PD控制对柔性板的大幅值振动抑制效果明显.但后续柔性板一直处于小幅值残余振动状态,到30 s左右才基本抑制到0.5%以内,可见PD控制对柔性板的抑制仍具有一定的局限性. 图6 PD振动控制曲线Fig. 6 Vibration curve under PD control (3) 迭代学习控制实验结果 柔性铰接板的迭代学习控制实验中,算法选用变遗忘因子的闭环迭代学习控制算法,其学习律为式(11)所示,经多次实验后选取到的参数为:学习增益Γ=0.02,学习增益Φ=0.86,遗忘因子函数中a=0.482,b1=2.2,b2=27,c1=1.6,c2=10;学习时间t⊂[0,T],T取30 s,学习次数7次.控制量向后移20个采样周期后开始控制. 如图7所示为遗忘因子函数的变化趋势.该遗忘因子函数可保证在控制的初始阶段和临近截止阶段两个区间段上,上一次迭代学习的控制量对本次学习的影响小,而在其余区间段影响大. 图7 遗忘因子的变化趋势Fig. 7 Variation trend of forgetting factor 如图8(a)、8(b)、8(c)、8(d)、8(e)、8(f)、8(g)分别为柔性铰接板的第1次、第2次、第3次、第4次、第5次、第6次、第7次迭代学习控制的振动响应曲线,8(h)、8(i)、8(j)、8(k)、8(l)、8(m)、8(n)为对应的控制量曲线. 到了第2次迭代学习,经验算第2次迭代后柔性板会在17 s左右衰减到2%的小幅值范围;但之后会持续较长时间的小幅值残余振动,到29 s左右基本抑制到0.5%以内.对比图8(a)与图8(b)可见,相比于第1次迭代,柔性板在第2次迭代控制作用下大幅值振动衰减效果比第1次迭代快8 s左右,但小幅值残余振动的抑制效果比第1次迭代只快1 s左右,说明小幅值的振动抑制提升不大,这一点从控制量曲线上也可以看出. 到了第4次迭代,经验算第4次迭代后柔性板会在14.5 s左右衰减到2%的小幅值范围,而后在20.5 s左右将小幅值残余振动抑制到0.5%以内.对比图8(b)与图8(d)可见,第4次迭代学习后,柔性板的大幅值快速衰减效果比第2次迭代快2.5s,小幅值残余振动抑制效果比第2次快8 s左右,说明不论是大幅值的快速衰减还是小幅值的振动抑制都得到较大提升,这一点从控制量曲线上也可以看出. 到了第5次迭代,经验算第5次迭代后柔性板会在14 s左右衰减到2%的小幅值范围,而后在20 s左右将小幅值残余振动抑制到0.5%以内.对比图8(d)与图8(e),柔性板的大幅值快速衰减效果比第4次迭代只快0.5 s,耗时相近;与此同时小幅值的残余振动抑制效果比第4次迭代也只快0.5 s,耗时相近,说明不论是大幅值的快速衰减还是小幅值的残余振动,迭代学习控制的改善效果已放缓,这一点从各自的控制量曲线也可以看出. 到了第7次迭代,经验算第7次迭代后柔性板会在14 s左右衰减到2%的小幅值范围,而后在20 s左右将小幅值残余振动抑制到0.5%以内.对比图8(e)与图8(g),这一次柔性板的大幅值快速衰减效果和第5次迭代的效果相同,均为14 s左右;与此同时小幅值的残余振动抑制效果也与第5次迭代的效果相同,均约20 s,说明这一次迭代后控制的改善效果很小. 图8 迭代学习振动控制曲线Fig.8 Vibration curve under iterative learning control 如图9所示,为迭代学习控制效果(柔性板振幅衰减到2%用时)随迭代次数的变化关系.从图上可见从第1次迭代到第5次迭代这一过程中,柔性板大幅值快速衰减的耗时从21 s逐步减少到了14 s,说明随着迭代次数的增加,柔性板的大幅值快速衰减效果在逐步提升,但改善效果在逐步放缓.到了第6次、第7次迭代时,柔性板大幅值衰减的耗时均约14 s,与第5次迭代的效果相同,说明当前条件下迭代学习控制表现出了收敛的特性.在此选用第5次迭代作为本实验最终的学习控制效果. 图9 迭代学习控制效果随迭代次数的变化关系Fig. 9 Relationship between the effect of iterative learning control and the times of iteration 将图8(e)的学习控制效果和图6(a)的PD控制效果作对比发现,柔性板的初始振幅都在10±0.2 mm附近,PD控制在21 s左右进入小幅值振动范围,在30 s左右才基本抑制到0.5%以内;第5次迭代学习控制在14 s左右即进入小幅值振动范围,在20 s左右将小幅值残余振动抑制到0.5%以内,对比PD控制,迭代学习整体的抑振效果提高了近33%,可见5次迭代后的控制效果明显优于PD控制. 本文研究了柔性铰接板的弯曲振动特性,使用了压电陶瓷传感器检测柔性板的振动信息,以此振动信息为反馈输入,设计了变遗忘因子的迭代学习控制器对柔性铰接板的振动进行主动控制,同时以PD控制器的振动控制效果作对比.实验结果表明,在此选用第5次迭代作为本实验最终的学习控制效果,对比PD控制,迭代学习整体的抑振效果提高了近33%,可见迭代学习控制效果明显优于PD控制.


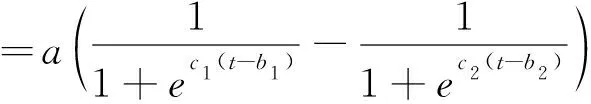

3 实 验





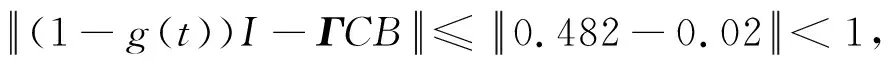


5 结 论

