基于解耦双通道线性自抗扰控制的连续型机械臂轨迹跟踪策略*
张月龄,向国菲,税懿,佃松宜*
0 引 言
连续型机械臂是一种具有柔性化结构的机械臂,其结构紧凑、弯曲性能良好,在外骨骼系统[1]、农业采摘[2]、外科手术环境[3-4]、以及飞机油箱[5]等人员和传统刚性机械臂难以到达或危险的环境有着广泛的应用前景.在这些应用场景里,连续型机械臂常搭载检测和操作工具,如内窥镜、手术钳和机械爪等,实现特定的操作任务,那么,高性能轨迹跟踪控制是实现这些应用的重要基础技术.目前用于连续型机械臂控制的有计算力矩法[6-7]、混合力/位置闭环控制法[8]、反馈线性化[9],但这些控制方法高度依赖精确的系统模型.由于连续型机械臂本质的非刚性结构,在使用几何分析法[10]、欧拉-拉格朗日法[11]、虚功法[12]等建模方法时,得到的模型或者太过复杂而难以基于此设计控制器;或者忽略系统未建模动态、未知干扰等因素,从而导致基于上述控制方法得到的控制器难以实现良好的控制性能.因此,针对连续型机械臂缺乏精确模型、存在多源不确定性的情况,设计何种控制策略实现对连续型机械臂的高精度轨迹跟踪,这一问题有着重要的理论和现实意义.
考虑系统不确定性,文献[13]首次将鲁棒控制用于连续型机械臂,但鲁棒控制主要针对系统内部小范围的不确定性,对较大未知外部扰动的处理能力有限,且需单独考虑内部不确定性、外扰等因素设计控制器,使控制器复杂保守.文献[14]用神经网络对连续型机械臂进行系统辨识,文献[15]和文献[16]利用模糊系统作为逼近器,虽然实现了对连续型机械臂的控制,但神经网络、模糊控制器中需手动整定的参数过多,运算量大,神经元的权值或模糊规则的训练时间长,在工程实现上存在困难,目前仍较少应用于实际连续型机械臂控制.
自抗扰控制(active disturbance rejection control, ADRC)将被控对象的内部不确定性和外部干扰统一视作“总扰动”[17,18],并利用扩张状态观测器(extended state observer, ESO)对其实时估计,然后通过反馈对控制量进行补偿,达到在干扰产生影响前消除可能产生误差的作用[19],实现主动抗扰.ADRC中“总扰动”的设计思想避免了对每一可能出现的不确定性分别设计控制器,简化控制器结构,使其更易于工程实现.ESO实时观测、获取估计量的能力,避免了神经网络、模糊控制等方法的长时间离线训练过程.同时,ESO具备的状态观测功能,可以实现对输出的各阶导数进行观测,在控制系统部署时可节省相应传感器.这些优势对结构紧凑连续型机械臂的轨迹跟踪控制有着重要的实际意义.
传统ADRC的设计采用非线性函数,虽然具备实现良好的控制效果的能力,但其参数整定困难,控制性能受参数整定的影响,不利于实际工程应用.基于此,文献[20]提出的线性自抗扰控制(linear active disturbance rejection control, LADRC),结构比较简单,对非线性系统同样具备较强抗扰能力,在工业生产线[21]、飞行器[22]、刚性机器人[23]等对象的控制中应用广泛.据作者所知,该方法尚未应用于柔性化的连续型机械臂系统.本文所考虑的线驱连续型机械臂是典型的强耦合非线性的MIMO系统,解耦设计是控制的难点,文献[24]在对双连杆机械臂设计自抗扰控制器时,忽略了双关节间的耦合影响.文献[25]考虑耦合影响,利用虚拟控制量与LADRC结合,实现了对多输入多输出系统的解耦,但未考虑解耦率未知的情况.文献[20]和文献[26]在理论层面提出了解耦率未知时的自抗扰控制器设计,但未应用于实际对象.
基于此,针对连续型机械臂末端轨迹跟踪,本文提出基于解耦策略的线性自抗扰控制方案.首先,引入虚拟控制量实现对MIMO系统的解耦;然后,对解耦后的系统并行设计双通道线性自抗扰控制器.考虑系统中存在未知解耦率、未建模动态、未知外部扰动等情况,将多源不确定性估计问题转化为 “总扰动”的抗扰问题,进一步利用“扩张状态”思想,转换为状态估计问题.采用线性扩张观测器,基于“带宽法”调整观测器参数.采用Lyapunov稳定性理论证明该线性扩张观测器的收敛性,得到估计值,实时反馈并补偿控制量,进而实现不确定条件下连续型机械臂的高精度轨迹跟踪控制.
1 问题描述
本文以典型的线驱连续型机械臂为研究对象,其结构如图1 所示,由主骨架、驱动线(次骨架)和圆盘组成,骨架利用NiTi合金的超弹性能实现柔性,圆盘采用轻质铝材,小孔互成120°分布.末端圆盘可搭载内窥镜等检修设备.给驱动线施加驱动力矩τ1和τ2后,驱动线产生伸缩形变,从而带动机械臂实现连续的弯曲运动.
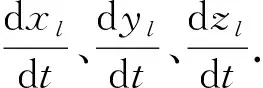
Ek=Ekl+Ekp=
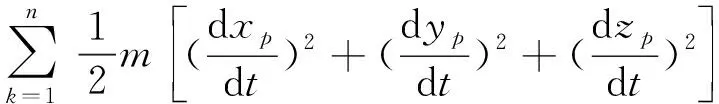
(1)
其中ρ和A表示骨架的密度和横截面积,m表示支撑盘的质量.
连续型机械臂的势能由弹性势能和重力势能两部分组成,通过实验表明[11]计算时可将重力势能忽略,因此连续型机械臂的弹性势能表示为:
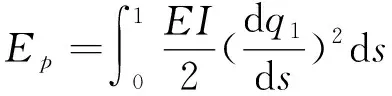
(2)
其中EI表示骨架的刚度,q1表示弯曲角,并且用q2表示旋转角.
假设p1和p2代表在力矩τ1和τ2作用下的位移,则系统在某一确定位姿下的广义力可表示为[11]:
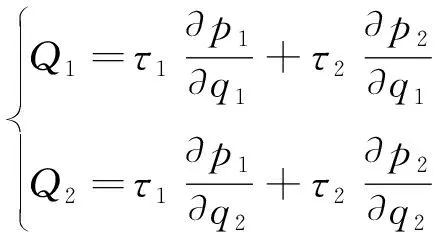
(3)
由理论力学得系统拉格朗日第二类方程为:
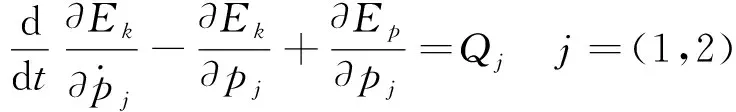
(4)
将式(1)、(2)代入式(4),可得到连续型机械臂动力学微分方程[11]形式如式(5)所示:
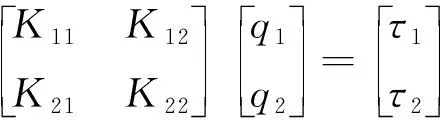
(5)
但是由于连续型机械臂非刚性的结构特点,由运动学求解得到的速度表达式高度非线性强耦合,十分复杂[5],难以用于后续动力学推导,导致式(5)中具体参数Mij、Cij、Kij(i=1,2;j=1,2)难以获得;或者对推导过程中的复杂中间参数采用最小二乘拟合[11]等方式进行简化,导致建立得到的动力学参数Mij、Cij、Kij(i=1,2;j=1,2)不够准确,从而进一步导致基于动力学设计的控制器难以实现良好的控制性能.因此,本文分别考虑动力学方程中Mij、Cij、Kij(i=1,2;j=1,2)存在不确定性的情况,提出控制策略以抑制不确定性对控制性能的不利影响.
2 控制器设计
2.1 解耦控制
式(5)描述的连续型机械臂动力学模型可写为

(6)
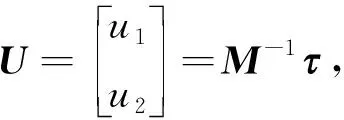
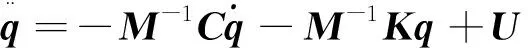
(7)
即可将解耦后的系统(7)看作并行的两个SISO系统如式(8)所示,可对其设计相同结构的控制器.
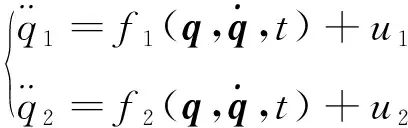
(8)

(9)


(10)
由上式可知,通过选择适当的增益kai(i=1,2)和kbi(i=1,2),跟踪误差可渐近收敛至零.
2.2 线性自抗扰控制
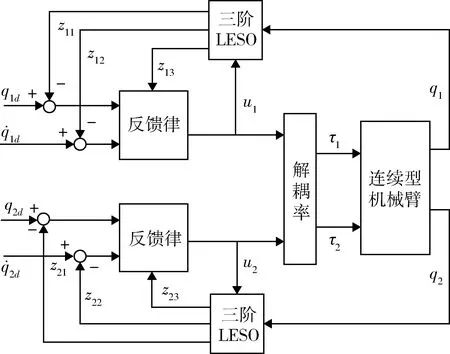
图2 LADRC控制框图Fig.2 Control diagram of LADRC
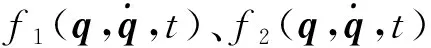

(11)
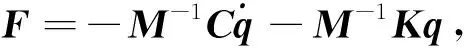
同理,若考虑未知外部干扰d,式(7)表示为
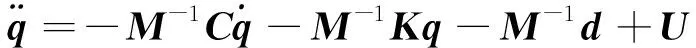
(12)
当解耦率M未知时,此时将系统(6)看作式(13)的形式

(13)
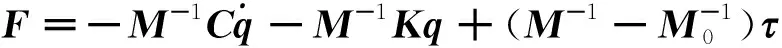
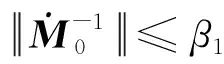
(14)

(15)
其中β1、β2为定常正数.
同理可由系统(13)得到式(11)的形式.将系统(11)看作解耦后得到的两个系统,如式(16)、(17)所示:
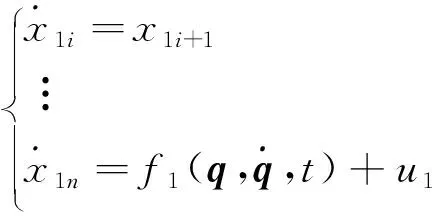
(16)
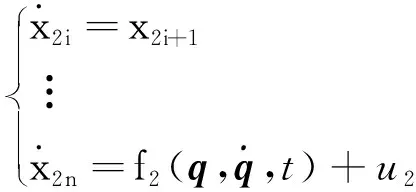
(17)
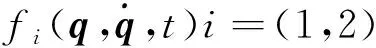
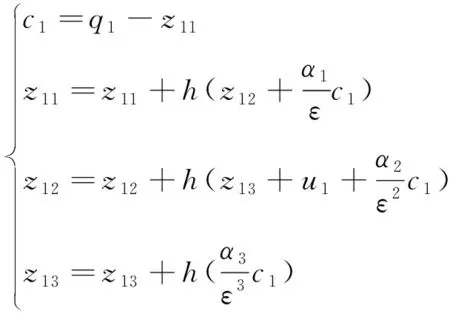
(18)

(19)
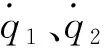
利用线性扩张观测器得到的观测量,设计反馈控制律如下式所示:
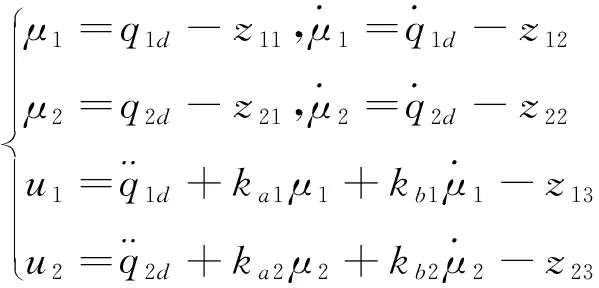
(20)
当解耦率已知时,解耦后得到作用于被控对象的控制量为
τ=M·U
(21)
当解耦率未知时,利用解耦率估计值得到作用于被控对象的控制量为
τ=M0·U
(22)
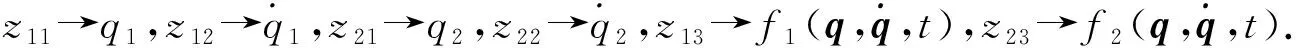
证明.
=-α1η1+η2
(23)
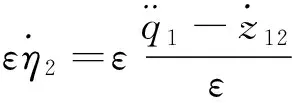
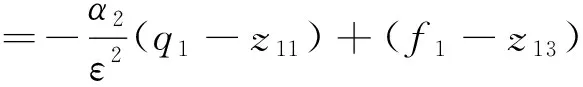
(24)

(25)
则观测误差状态方程可写为:
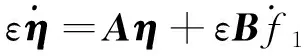
(26)

矩阵A的特征方程为:
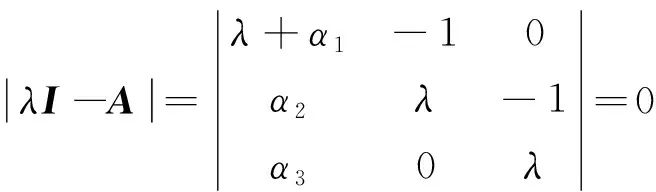
(27)
由特征方程即可得:
λ3+α1λ2+α2λ+α3=0
(28)
对α1,α2,α3取值使上式其满足Hurwitz,则对于对称正定阵Q,存在P满足Lyapunov方程:
ATP+PA+Q=0
(29)
设Lyapunov函数为:
V0=εηTPη
(30)
对其求导可得:

(31)

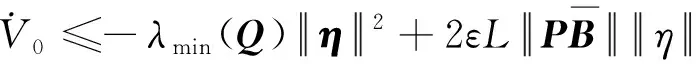
(32)

(33)
同理对线性扩张观测器(19)也成立,由此定理1证明完毕,在保证参数满足式(33)的条件下,系统收敛.
由定理1可知,为确保LESO收敛,ε一般取较小值,但当LESO的初值与对象的初值不同时,起始阶段较小值的ε可能产生峰值现象,影响LESO的收敛效果,因此可设计ε为式(34)的形式:

(34)
其中R为常值参数.
3 仿真验证
为验证该控制方法对具强耦合、非线性特性的连续型机械臂的可行性,使用如下式所示的连续型机械臂动力学模型[8]对上述控制方法进行仿真验证,设计反馈控制律如式(20)、(21)、(22)所示,LESO如式(18)(19)所示:
其中

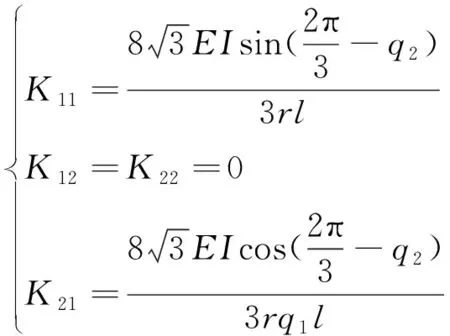
进行仿真的连续型机械臂参数选为:r=3,m1=1.086,m2=0.8,l=1.5,E=0.65,I=1.02,n=10,h=0.15.为验证对连续型机械臂旋转角、弯曲角的控制效果,跟踪函数设计为q2d=cos(1.2t),q1d=sin(1.2t-90°), LESO的参数取为α1=6,α2=11,α3=6,R=100,控制器参数取为kai=60(i=1,2),kbi=50(i=1,2).为验证算法的有效性,本文考虑了多种不确定性的情况进行讨论,为验证LADRC的抗扰能力和处理不确定性的能力,对同样的被控对象采用CTC进行仿真对比.
当系统模型精确已知,即ΔC、ΔK、d、ΔM为0时,两种控制方法的仿真结果如图3所示,在此基础上,进一步考虑未建模动态不确定性ΔC、ΔK、突加外部干扰d,解耦率不确定性ΔM,表示如下:

图3 模型精确已知时的轨迹跟踪图Fig.3 System tracking trajectories with known model
考虑突加外部干扰时的控制结果如图4所示,考虑未建模不确定性时的控制结果如图5所示,考虑解耦率不确定性时的仿真结果如图6所示.
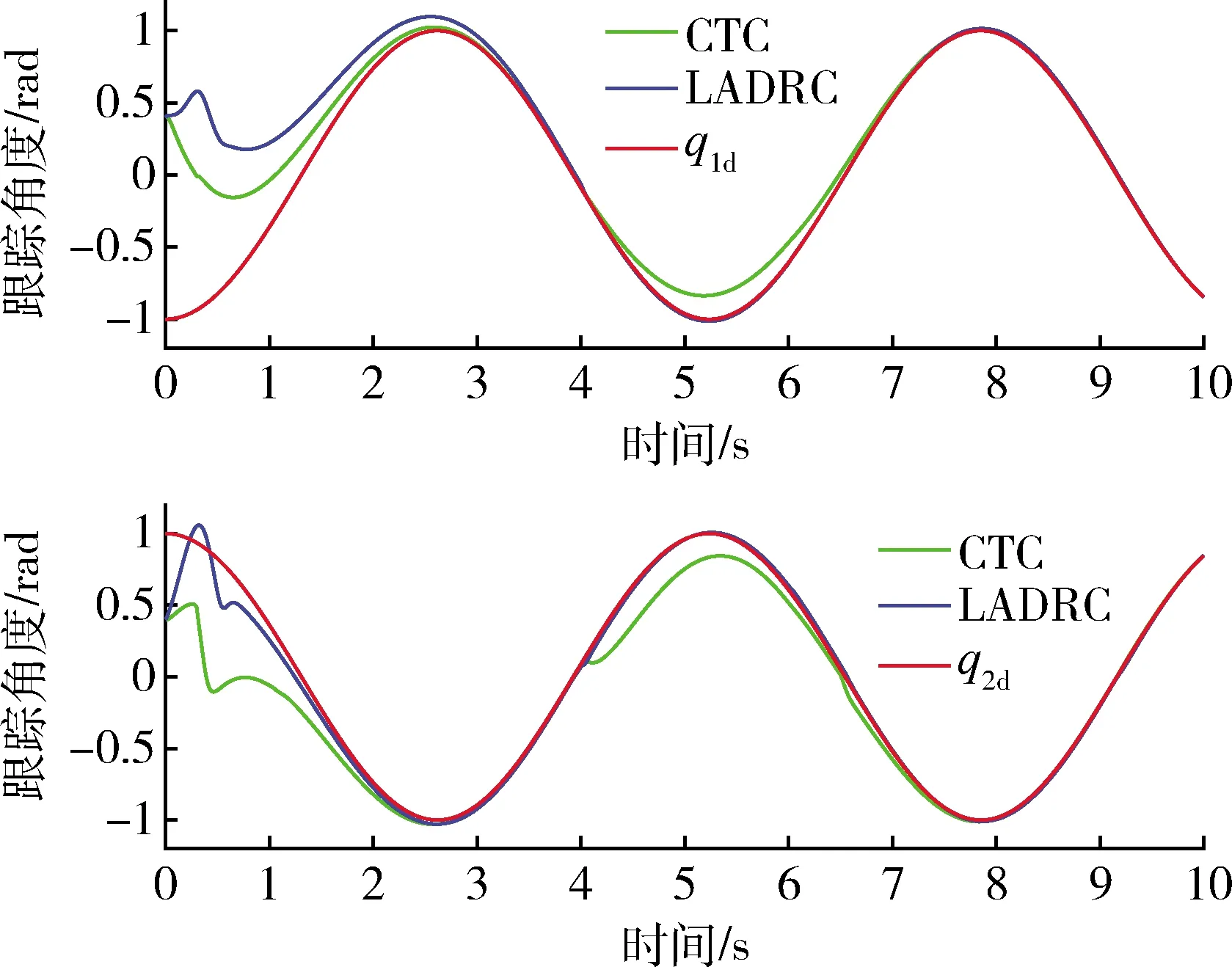
图4 突加外部干扰时的轨迹跟踪图Fig.4 System tracking trajectories with external disturbances
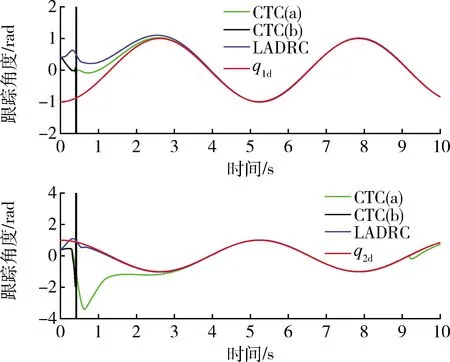
图5 含未建模不确定性时的轨迹跟踪图Fig.5 System tracking trajectories with unmodeled dynamics
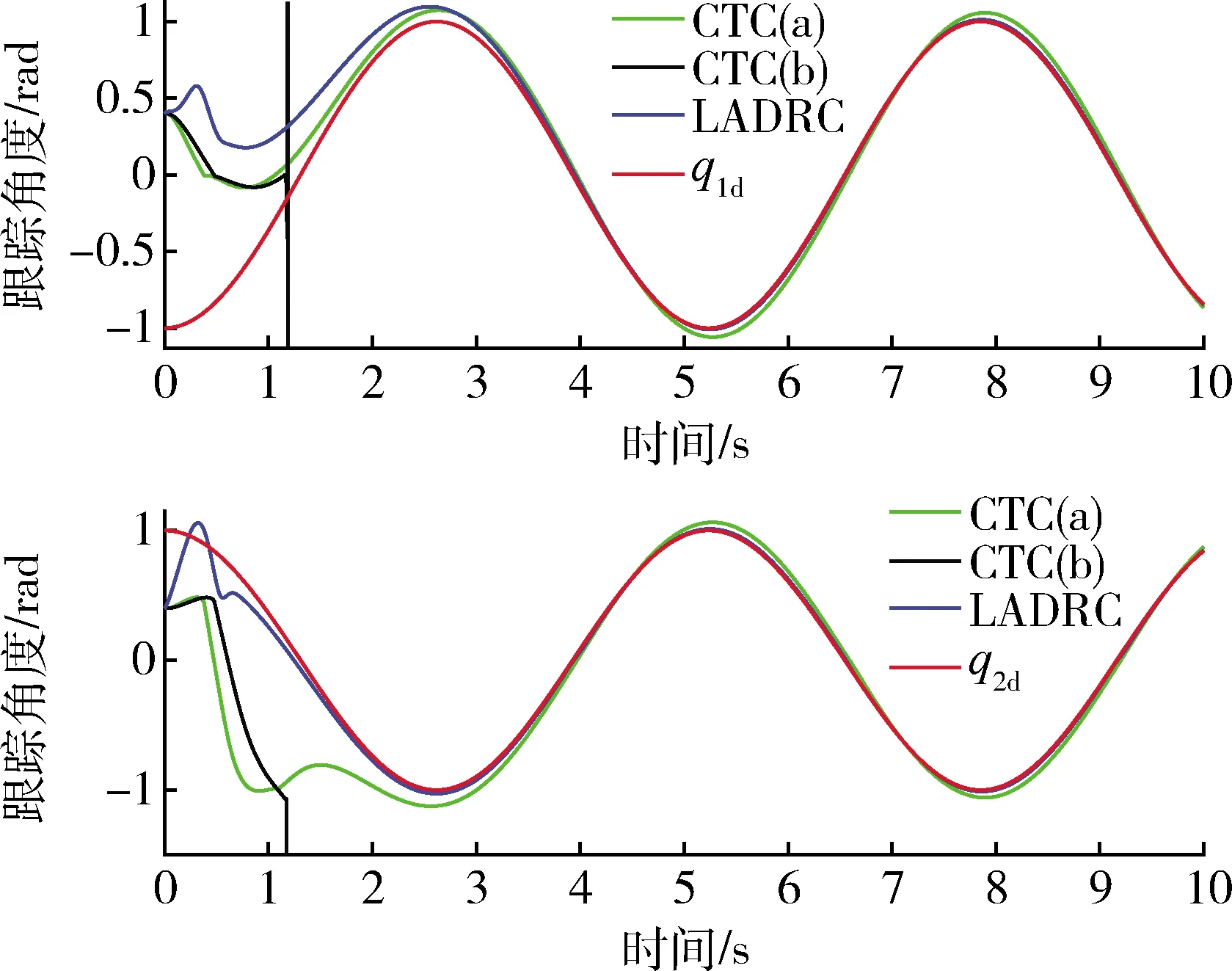
图6 含解耦率不确定性时的轨迹跟踪图Fig.6 System tracking trajectories with uncertain decoupling rate
以上结果表明,在被控对象模型精确已知的理想假设下,CTC和LADRC都能实现对目标轨迹的跟踪,且LADRC对q2有更好的控制性能,而CTC对q1有更好的控制性能,两种控制方法各有优劣.图4表明,4s时刻突加外扰后,LADRC受外部干扰影响小,而CTC受外扰影响出现了跟踪误差,且在6s时刻外部扰动消失后,仍需经过过渡时间才重新跟踪上目标轨迹.图5和图6表明存在未建模不确定、解耦率不确定时,与CTC相比,LADRC能以更小的误差快速实现轨迹跟踪.且当不确定性超过一定范围时,CTC失去控制,说明随着不确定性的出现,LADRC展现出比CTC更强的鲁棒性,抗扰性,能处理更大范围的不确定性,显示出更好的控制性能.
为进一步验证对连续型机械臂在更大范围不确定性情况下的控制效果,考虑解耦率M完全未知,同时系统模型参数C、K完全未知,且存在外部干扰d,三种不确定性同时存在的情况,此时仅利用连续型机械臂模型阶次信息设计三阶LADRC,得到仿真结果如图7~图9所示.
图7是q1、q2对目标轨迹的跟踪图,表明在仅知模型阶次信息的情况下,经过一段过渡时间后,LADRC能实现对连续型机械臂的轨迹跟踪.图8是LESO对实际角度、实际角速度的观测图像,图9是LESO对总干扰的观测图像,图8、图9验证了LESO能实现对连续型机械臂的状态观测和总干扰观测,图中的突刺,据分析是这一时刻两个角度的跟踪目标值重合,数值计算问题导致的,能在最终的轨迹控制中被LADRC处理.
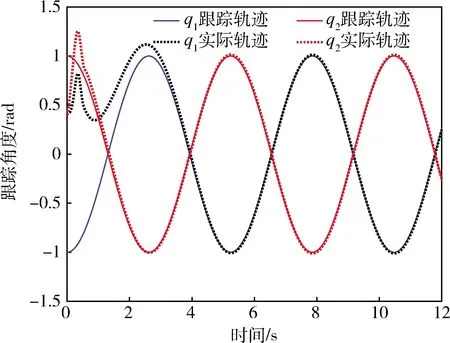
图7 解耦率未知、存在未建模动态和外部扰动时的轨迹跟踪图Fig.7 System tracking trajectories with unknown decoupling rate, unmodeled dynamics and external disturbance

图8 LESO状态观测图Fig.8 State observation of LESO

图9 LESO总干扰观测图Fig.9 Total disturbance observation of LESO
以上仿真结果表明,在连续型机械臂具有不确定性时,LADRC跟踪时间快,跟踪误差小,能处理更大范围的不确定性,抗扰能力更强,鲁棒性更好,展现出比CTC更好的控制性能.同时LADRC能在仅模型阶次信息已知的情况下,实现对连续型机械臂的控制,使这一控制方法不依赖于被控对象精确模型,对连续型机械臂的实际应用有重要意义.
4 结 论
本文针对包含多源不确定性的连续型机械臂轨迹跟踪问题,提出了基于解耦策略的LADRC控制方案.通过引入虚拟控制量实现对系统的解耦,并行设计双通道控制方案,针对解耦率已知和未知的不同情况分别设计LADRC控制器设计.采用LESO,简化系统参数整定,给出参数整定方法,基于Lyapunov稳定性理论证明了其收敛性.仿真验证中,综合考虑系统解耦率不确定性、未建模动态以及外部扰动,并将本文设计的控制方案与CTC相比,结果表明本文提出的控制方案,跟踪误差小,能处理更大范围的不确定性,有较强抗干扰能力和强鲁棒性.尤其是在三种不确定性同时存在,仅知模型阶次信息的情况下,基于解耦设计的LADRC能实现对连续型机械臂的轨迹跟踪.本文的控制方法结构简单,易于工程实现,对实际工业应用中连续型机械臂轨迹跟踪控制提供了新的方案.

