日心悬浮轨道混合推进航天器编队构型保持研究*

左晨熠，袁长清*，龚胜平，贺京九

0 引 言

深空探测任务通常要求长航时且对整体重量有限制，为减少燃料及推进系统重量，先后提出多种推进方式，太阳帆推进是其中一种较为实用的方法.太阳帆推进是一种连续小推力的航天器推进方式，其通过太阳光子撞击帆面进行动量交换对太阳帆产生作用力.太阳帆推进的优势在于采用太阳光为动力，不需要消耗燃料，可持续对航天器加速，在长时间后能获得较大加速度.太阳帆推进的概念最早由Tsiolkovsky在1921年提出，目前已提出的利用太阳帆的空间任务有太阳帆的极地轨道[1]，水星轨道[2]，悬浮在黄道平面上的悬浮轨道[3]等.在太阳帆提供的连续推力的作用下，航天器可以实现悬浮轨道.悬浮轨道在中继通讯和深空探测任务中可提供轨道平台.GONG对悬浮轨道作了较多研究，将太阳帆悬浮轨道按照周期的不同分为3类[4].BOOKLESS等[5]研究总结了多类行星悬浮轨道的动力学模型，并总结出悬浮轨道的稳定区域.龚胜平针对地球及火星悬浮轨道，推导出在其附近的太阳帆编队的线性化相对运动方程，并分析了能使其稳定的区域[6].陈翠红在Bookless的研究基础上，进一步对行星悬浮轨道的稳定性进行了分析[7].太阳帆受到的光压力与太阳帆的面积、姿态都有关.当太阳帆处于不同的轨道时，太阳帆受到的光压力矩和各种引力梯度力矩也会发生变化，从而改变太阳帆的姿态.因此太阳帆的轨道和姿态是相互耦合的，现有文献对太阳帆进行研究时通常认为只考虑太阳帆姿态调节对轨道的控制.对航天器编队加入系统内力以直接控制航天器距离可以简化航天器编队控制且减少响应时间.航天器库仑力编队通过使航天器带电形成排斥力或吸引力来控制航天器编队的构型、姿态、距离等，由KING[8]首次在2002年提出.三星库仑卫星编队最早由Hanspeter展开研究，通过设计反馈控制来实现编队的保持和重构[9].SAAJ[10]首次提出了以库仑力为主、电推进为辅的混合推进方式.航天器间库仑力作为系统内力不会影响整个编队系统的在轨运行且不需要消耗燃料，可以提供长周期稳定的控制力.

本文建立了日心悬浮轨道附近的混合推进航天器编队的相对运动方程，基于该方程并考虑轨道出现初始小扰动的情况，设计了LQR控制器，通过调节太阳帆的姿态及航天器间库仑力的大小对航天器进行控制.通过数值仿真的方式对编队长周期运行情况进行分析，验证了设计方法的有效性.

1 航天器动力学建模

如图1所示，惯性坐标系中X轴指向J2000星历的春分点，Z轴方向为地球公转的角速度方向，Y轴与X轴和Z轴构成右手坐标系，坐标原点为太阳质心.设编队中的主航天器运行在离OXY平面距离为h，半径为ρ的圆轨道上，角速度为ω.定义旋转坐标系oξζη，坐标原点为主航天器的质心位置，ξ轴沿上述圆轨道的圆心指向主航天器的方向，η轴的方向定义为主航天器的轨道角速度方向.

图1 日心悬浮轨道Fig.1 Displaced solar orbit

设主航天器对太阳的矢径为rm，从航天器对太阳的矢径为rs，则从航天器相对主航天器的矢径为δ=rs-rm.

在惯性坐标系中，两航天器的轨道动力学方程可表示为

(1)

(2)

由式(1)(2)得到在惯性坐标系下的相对运动方程为：

fg(rs)+fm(rs)-fm(rm)+

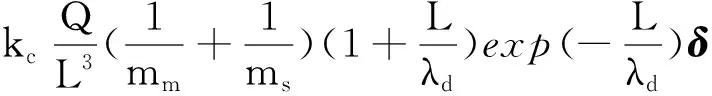
(3)

将惯性系下的方程转换到旋转坐标系oξζη中，有如下关系成立：

(4)

fg(rm)-fg(rs)+fm(rs)-fm(rm)+

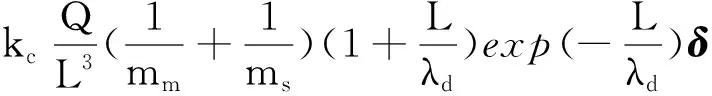
(5)

(6)

考虑到从航天器在主航天器附近运动，从航天器的太阳帆参数(法向方向和太阳光压因子)与主航天器非常接近，于是可以将fm(rs)-fm(rm)在(rm,nm,βm)处展开，取线性项得：

(7)

可得在oξζη旋转坐标系下的线性化相对运动方程：

(8)

在轨道坐标系下，式(8)中各项可写成如下分量形式：

δ=[xyz]T

(9)

ω=[0 0n]T

(10)

rm=[rm0 0 ]T

(11)

rs=[rm+xyz]T

(12)

(13)

将式(9)～(13)代入式(8)整理得相对运动方程的分量形式：

(14)

其中fcx，fux，fcy，fuy，fcz，fuz分别为各力沿轨道坐标系3个坐标轴的分量.

设主航天器沿圆轨道运动，轨道角速度不变，有：

(15)

(16)

ω×(ω×δ)=[-n2x-n2y0]T

(17)

相对运动方程的分量形式变为：

(18)

由于航天器距太阳距离较远，近似认为悬浮轨道处太阳光线为平行光，方向沿旋转坐标系η轴，所以α即为太阳帆的法向方向与η轴的夹角，在之后的运算中用φ替代α，设θ为太阳帆的法向方向在旋转坐标系oξζ平面内与ζ轴夹角.太阳帆的法向矢量可以表示为：

n=[sinφsinθsinφcosθcosφ]T

(19)

将式(6)，(7)，(19)代入式(18)得到相对运动方程的分量形式为：

(20)

取主航天器与从航天器为相同航天器，面质比相同，δβ=0.则进一步简化后的相对运动方程为：

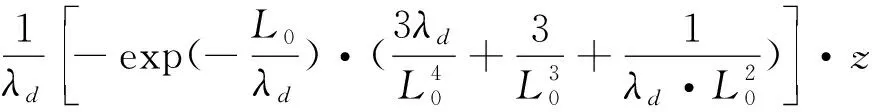
(21)

2 控制器设计

对式(21)中状态变量及控制输入用下式进行表示：

(22)

其中x0，y0，z0为从航天器跟踪参数轨道运动时的期望值，δx，δy，δz为状态误差.φ0，θ0，Q0为保持从航天器跟踪参数轨道运动时的控制量，δφ，δθ，δQ为调整状态误差所需要的调整控制量.

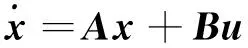
(23)

取如下二次型性能指标函数：

(24)

式中Q与R分别为描述状态变量和控制变量的加权矩阵，此LQR问题对应的代数Riccati方程为：

PA+ATP-PBR-1BTP+Q=0

(25)

解得最优控制u=-R-1BTPx.

3 仿真分析

假设主航天器运行的悬浮轨道参数为ρ=0.98AU，h=4×105km，从航天器运行在oξζ平面内的半径为100 m的圆形轨道，轨道中心点为主航天器质心，轨道周期选取为地球公转周期的1/100.光压因子取β=0.20.仿真模型为存在一个δx=10 m的初始误差的理想二体动力学模型，仿真在初始时主航天器不存在初始速度误差，初始速度误差会在编队仿真过程中对航天器间距离产生影响，并累积较快.利用控制输入使得从航天器回到参考轨道.仿真结果如下图所示.

图2为在LQR控制器控制下的相对运动轨道，表明从航天器在预设参考轨道上稳定运行.图3、图4为从航天器的两个太阳帆姿态角的变化，稳定持续提供小推力控制.图5为电荷积大小变化，通过控制电荷积大小调整库仑力大小.如图示，在仿真过程中通过调整电荷积数值用时约10h消除初始距离误差，使航天器间距离达到期望距离，电荷积在之后的仿真过程中为小量且不再变化，为直观展示前10h内电荷积变化，图5不再展示15h后仿真过程中的电荷积变化曲线.仿真结果表明编队在长周期内保持稳定，且能量消耗小.

图2 相对运动轨道Fig.2 Relative motion orbit

图3 姿态角变化Fig.3 Attitude angle change

图4 姿态角变化Fig.4 Attitude angle change

图5 电荷积变化曲线Fig.5 charge’s change

4 结 论

本文主要研究了太阳帆和库仑力混合推进航天器编队在日心悬浮轨道上的动力学与控制问题.对原始方程进行线性化处理，得到在日心悬浮轨道附近的线性化相对运动方程.通过控制太阳帆的两个姿态角及航天器间库仑力大小，对编队构型进行改变或保持.基于上述方程设计了LQR控制器.该方法比仅使用太阳帆作为编队推进更加简单可控且响应速率更高.为验证该控制器的有效性与控制性能，通过软件仿真平台对编队模型在参考轨道处进行数值仿真，结果显示编队在有初始扰动量的情况下能快速调整至参考轨道，并在长周期内保持稳定.