阶梯圆环压电超声换能器径向振动性能的理论研究∗
许 龙 范秀梅
(中国计量大学理学院 杭州 310018)
0 引言
径向振动压电陶瓷复合换能器具有辐射面积大[1]、辐射效率高[2]、径向辐射均匀以及径向灵敏度高等突出优点[3−4],在水声发射和接收[5]、超声降解[6]、超声拔丝拔管等方面得到了广泛的应用[7−8]。这种换能器是由压电陶瓷圆环/圆管与金属圆环/圆管径向复合而成[9]。金属圆环/圆管可以改善压电陶瓷圆环的散热[10],提高换能器的功率容量[11];改变金属圆环的结构参数,可以调节换能器的工作频率以满足不同的应用场景[12]。
为了适用于径向超声滚动切割或径向超声滚焊的应用需求[13−14],设计了一种由压电陶瓷圆环和阶梯型金属薄圆环复合而成的径向振动压电超声换能器。根据力电类比原理建立了阶梯型金属薄圆环径向振动的等效电路,推导了其径向共振频率方程和位移放大系数,根据理论模型和有限元仿真模拟分析了阶梯型金属薄圆环的径向振动性能。在此基础上进一步建立了阶梯圆环压电超声换能器的等效电路,推导了其共振和反共振频率方程,根据理论推导和有限元仿真模拟研究了阶梯圆环压电超声换能器的径向振动性能。本文研究的阶梯圆环径向振动压电超声换能器与目前应用于超声滚焊和超声切割的换能器在结构及工作原理上均不同。现有的超声滚焊系统主要是通过夹心式压电超声振动系统的纵向振动实现超声滚动焊接,超声振动系统的尺寸通常大于等于3个半波长;应用于超声切割的振动系统也是由夹心式压电换能器、超声变幅杆和切割刀的纵向振动实现食品或橡胶的切割,其振动系统的尺寸也较大,并且不能通过振动系统的滚动实现连续超声切割;为此本文提出了一种几何尺寸更小的阶梯形径向超声换能器,通过选择换能器的二阶径向共振模式,实现超声能量由内向外聚焦以及换能器与外部设备在径向位移节点处连接固定,从而实现通过换能器的滚动进行连续的超声切割或焊接的功能。
1 阶梯圆环径向振动特性分析
1.1 径向振动金属薄圆环的等效电路
图1所示为金属薄圆环选择柱坐标系统{r,θ,z}。当圆环轴向厚度远小于圆环的平均半径时,圆环的轴向应力近似为零(即可忽略纵向耦合)[15],此时金属薄圆环做纯径向简谐振动[16]。图1中R、R1和h1分别为金属薄圆环内外半径和轴向厚度,V1和V2、F1=−Tr1S1和F2=−Tr2S2以及S1=2πRh1和S2=2πR1h1分别为金属薄圆环内外侧面处质点的径向振动速度、径向应力和侧面面积。根据文献[17]可知金属薄圆环径向波动方程为
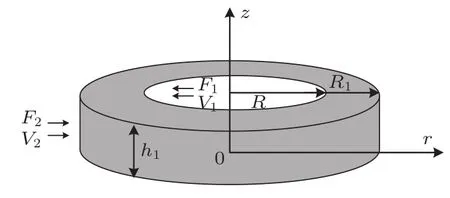
图1 金属薄圆环Fig.1 Thin metal ring
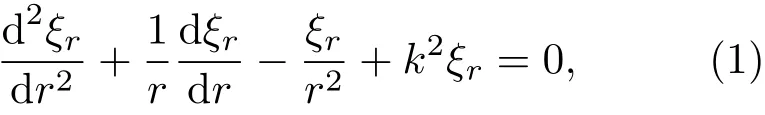


圆环的径向振动速度:

其中,A1、B1为待定系数。
金属薄圆环的径向振动应力方程为[18]

将式(2)代入式(4)可得
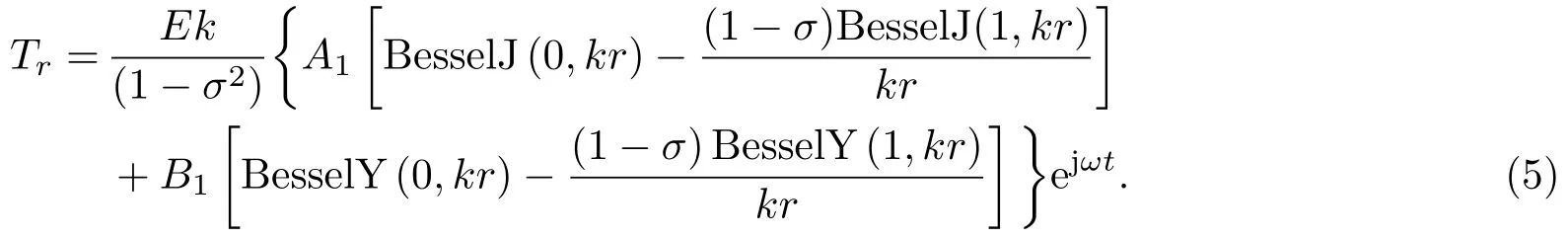
将R、R1、V1、−V2代入式(3)中,可以求出待定系数A1和B1的表达式分别为

将式(6)、式(7)代入式(5)中,可得

化简式(8)可得

其中:

根据力电类比原理[9],由式(9)可得如图2所示的非互易二端口等效网络,即金属薄圆环等效电路图。

图2 金属薄圆环径向振动等效电路Fig.2 Radial vibration equivalent circuit of a thin metal ring
1.2 阶梯圆环径向振动等效电路、共振频率方程和位移放大系数
阶梯圆环可看作由图3所示的两个轴向厚度不同的金属薄圆环径向复合而成,其轴向厚度沿半径方向的变化规律为

图3 阶梯圆环结构示意图Fig.3 Schematic diagram of stepped metal thin ring structure

R1、R2和h2分别为外圆环内半径(内环外半径)、外半径和轴向厚度,V3和V4、F3=−Tr3S3和F4=−Tr4S4以及S3=2πR1h2和S4=2πR2h2分别为外环内外侧面处质点的径向振动速度、径向应力和侧面面积。将R1、R2、V3、−V4代入式(3)中,可求出外环径向位移方程中的待定系数A2和B2:

由图3可知,阶梯圆环做径向振动时,内外环两部分连接处满足径向应力和速度连续,由图2所示的金属薄圆环径向振动的等效电路和内外环两部分之间的边界条件可得图4所示的阶梯圆环等效电路。
图4中内环部分的各等效阻抗参数在1.1节中已给出,外环各部分阻抗参数分别为

其中,Z3=ρcS3,Z4=ρcS4。
当外环的外侧面为自由端,即F4(F4=0)处短路时,根据图4推导出阶梯圆环的输入阻抗为

阶梯圆环的径向共振频率方程为

将1.1节中的A1、B1和1.2节中的A2、B2代入式(2)中,可求出内环和外环的内外侧面质点位移ξr1(R)、ξr1(R1)和ξr2(R1)、ξr2(R2),进一步可得阶梯圆环的位移放大系数M为
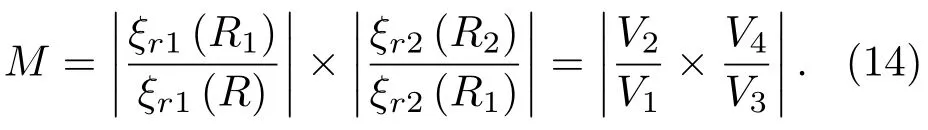
由式(12)结合图4可得
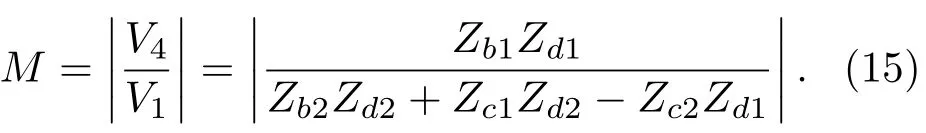

图4 阶梯圆环等效电路Fig.4 The equivalent circuit of a stepped metal thin ring
1.3 阶梯圆环径向振动性能分析
选取阶梯型圆环的材料为硬铝,材料参数σ=0.33,E=71 GPa,ρ=2810 kg/m3。阶梯圆环的内外环轴向厚度分别为10 mm和3 mm,改变内环的外半径,可得其一阶、二阶径向共振频率与内外环径向厚度之比K1的变化关系,其中K1=(R1−R)/(R2−R1)。理论计算和仿真结果如图5和表1所示。
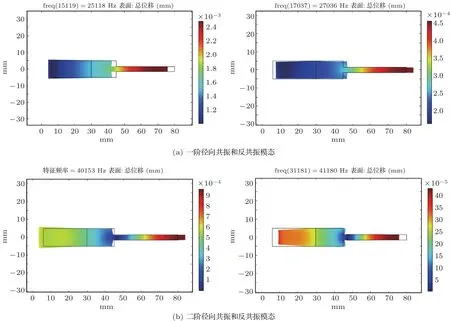
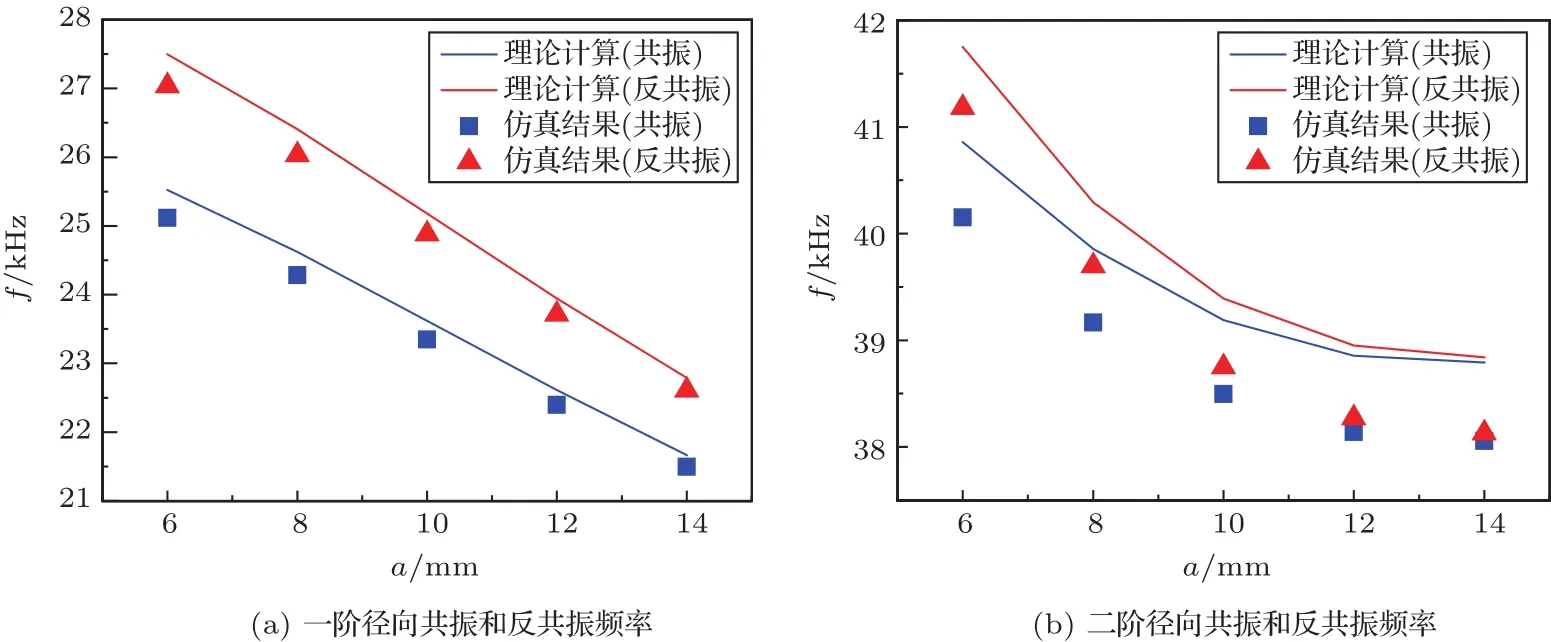
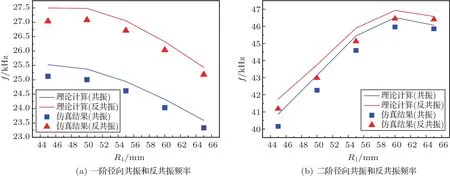
图5(a)、图5(b)分别是理论计算和有限元仿真模拟得到的一阶、二阶共振径向位移放大系数M随内外环径向厚度之比K1的变化关系曲线。由图5可知,K1值逐渐增大(即内环半径增大,外环半径减小),阶梯圆环的一阶径向共振位移放大系数先迅速减小后平缓增大,且M值始终小于1,即在一阶径向共振模式下阶梯圆环的内部径向位移大外部径向位移小,及阶梯圆环未能实现由内到外的径向位移振幅放大;二阶径向共振位移放大系数先增大后减小,内外环半径比在0.250 图5 阶梯圆环一阶、二阶径向共振位移放大系数M与内外环径向厚度之比K1的关系Fig.5 The relationship between the first-order and second-order radial resonance displacement ampli fication coefficient M of the stepped ring and the radial thickness ratio K1of the inner and outer rings 在表1中,fa1和fa2分别表示理论计算得出的一阶和二阶径向共振频率值,fb1和fb2分别为仿真模拟得出的一阶和二阶径向共振频率值,Δf1ab和Δf2ab分别为两种方法计算得出的一阶、二阶径向共振频率值的相对误差。由表1可知,K1值增大,阶梯圆环的一阶径向共振频率随之减小,二阶径向共振频率随之增大,且二阶共振频率变化幅度大于一阶共振频率;两种方法计算的一阶径向共振频率的相对误差小于0.25%,二阶径向共振频率的相对误差小于4.5%。 表1 阶梯圆环一阶和二阶径向共振频率随内外环径向厚度之比K1变化的理论值与仿真值Table 1Theoretical and simulated values of the first-and second-order radial resonance frequency of the stepped ring as a function of the radial thickness ratio K1of the inner and outer rings 设置阶梯圆环内环的内外半径(外环的内半径)和外环的外半径分别为30 mm、45 mm和80 mm,改变外环的轴向厚度,可得其一阶、二阶径向共振频率与内外环轴向厚度之比K2的变化关系,其中K2=h1/h2。理论计算和仿真结果如图6和表2所示。 表2 阶梯圆环一阶和二阶径向共振频率随内外环轴向厚度之比K2变化的理论值与仿真值Table 2Theoretical and simulated values of the first-and second-order radial resonance frequency of the stepped ring as a function of the axial thickness ratio K2of the inner and outer rings 图6 阶梯圆环一阶、二阶径向共振位移放大系数M与内外环轴向厚度之比K2的关系Fig.6 The relationship between the first-order and second-order radial resonance displacement ampli fication coefficient M of the stepped ring and the axial thickness ratio K2of the inner and outer rings 图6(a)、图6(b)分别是理论计算和有限元仿真模拟得到的一阶、二阶共振径向位移放大系数M随内外环轴向厚度之比K2的变化关系曲线。由图6可知,K2值逐渐增大(即内环轴向厚度增大,外环轴向厚度减小),阶梯圆环的一阶、二阶径向共振位移放大系数均增大;在一阶径向共振模式下阶梯圆环的内部径向位移大外部径向位移小,及阶梯圆环未能实现由内到外的径向位移振幅放大,内外环轴向厚度比在K2>2.25范围内,M值大于1,在此范围内阶梯圆环在二阶共振模式下能够实现由内向外的径向位移振幅放大。表2为理论计算和有限元仿真的阶梯圆环在不同的轴向尺寸下其一阶、二阶径向共振频率值。 由表2可知,K2值增大,阶梯圆环的一阶径向共振频率随之增大,二阶径向共振频率随之减小,且二阶共振频率变化幅度大于一阶共振频率;两种方法计算的一阶径向共振频率的相对误差小于0.25%,二阶径向共振频率的相对误差小于2.7%,由此可知,理论计算与仿真结果符合较好。 阶梯圆环压电超声换能器的结构如图7所示,换能器由内部压电陶瓷圆环和外部阶梯型金属薄圆环构成,图中a和R分别为压电陶瓷圆环的内半径和外半径,R1和R2分别为阶梯圆环的内环外半径和外环外半径。 图7 阶梯圆环压电超声换能器Fig.7 Stepped ring piezoelectric ultrasonic transducer 由文献[19]可知,压电陶瓷薄圆环的等效电路如图8所示。 其中,N31、C0r和S0分别为压电陶瓷圆环的机电转换系数、径向振动电容和横截面积,机械阻抗Z10、Z20和Z30的表达式分别为 压电陶瓷圆环与阶梯型金属薄圆环连接处满足机械上串联、电学上并联的边界条件[20],由图4和图8可得阶梯圆环压电超声换能器的整体等效电路如图9所示。 图8 压电陶瓷圆环径向振动等效电路Fig.8 Radial vibration equivalent circuit of piezoelectric ceramic ring 当Fa和F4两处短路时,即Fa=0、F4=0,由图9可得阶梯圆环压电超声换能器的输入机电阻抗为 图9 阶梯圆环压电超声换能器的等效电路Fig.9 The equivalent circuit of a stepped circular piezoelectric ultrasonic transducer 其中, 换能器的径向共振频率方程为 径向反共振频率方程为 表3 阶梯圆环压电超声换能器的共振、反共振频率和有效机电耦合系数的理论计算值和仿真值Table 3 Theoretical calculation and simulation values of the resonance,anti-resonance frequency and the effective electromechanical coupling coefficient of the stepped circular piezoelectric ultrasonic transducer 图10(a)和图10(b)分别为有限元仿真模拟得到阶梯圆环压电超声换能器的一阶、二阶径向共振和反共振模态振型图。由图10(b)可知,该换能器的二阶径向共振模态存在位移节圆,工程应用中可作为与外部设备的连接固定处。 图10 阶梯压电圆环超声换能器一阶、二阶径向共振和反共振模态Fig.10 First-order and second-order radial resonance and anti-resonance modes of stepped piezoelectric toroidal ultrasonic transducer 通过改变压电陶瓷圆环的内半径和阶梯型金属薄圆环中内环外半径尺寸,研究径向尺寸对换能器的一阶和二阶径向共振频率的影响规律。图11和图12分别为通过改变压电陶瓷圆环内半径和阶梯圆环的内环外半径,阶梯圆环压电超声换能器一阶和二阶径向共振和反共振频率随径向尺寸的变化关系曲线。由图11可知,随着压电陶瓷圆环内半径a增大,换能器的一阶径向共振和反共振频率逐渐减小,二阶径向共振和反共振频率逐渐减小并趋于接近,此时换能器的带宽将变窄,有效机电转换系数趋于零。由图12可知,随着阶梯圆环内环外半径R1增大,换能器的一阶径向共振和反共振频率逐渐减小,二阶径向共振和反共振频率先增大后减小。该结果对完善圆环形换能器的设计理论具有一定的指导意义和实际应用价值,对阶梯圆环压电超声换能器的工程应用提供理论参考。 图11 换能器的一阶、二阶径向共振和反共振频率与压电陶瓷圆环内半径的关系Fig.11 The relationship between the first-order and second-order radial resonance and antiresonance frequencies of the transducer and the inner radius of the piezoelectric ceramic ring 图12 换能器的一阶、二阶径向共振和反共振频率与阶梯圆环内环外半径的关系Fig.12 The relationship between the first-order and second-order radial resonance and antiresonance frequencies of the transducer and the outer radius of the inner ring of the step ring 本文设计了一种由压电陶瓷圆环和阶梯型金属薄圆环复合而成的阶梯环形压电超声换能器。根据力电类比原理建立阶梯型金属薄圆环径向振动的等效电路,推导了其共振频率方程和位移放大系数;在此基础上建立了阶梯圆环压电超声换能器的径向振动等效电路,推导其共振和反共振频率方程,分析了其径向振动性能。结合理论推导和仿真模拟的结果,探讨了径向尺寸对阶梯圆环压电超声换能器的径向振动的影响特性,结论如下: (1)随着阶梯圆环内环径向厚度增大,外环径向厚度减小,它的一阶径向共振频率逐渐减小,二阶径向共振频率逐渐增大,且二阶径向共振频率变化明显;阶梯圆环在一阶共振模式下环内径向位移振幅大于环外径向位移振幅,即阶梯圆环无法实现由内向外的位移振幅放大;当内、外环径向厚度之比在0.250 (2)随着阶梯圆环内环轴向厚度增大,外环轴向厚度减小,它的一阶径向共振频率逐渐增大,二阶径向共振频率逐渐减小;阶梯圆环在一阶共振模式下环内径向位移振幅大于环外径向位移振幅,即阶梯圆环无法实现由内向外的位移振幅放大;当内、外环轴向厚度之比在K2>2.25范围内,阶梯圆环在二阶共振模式下能够实现由内向外的位移振幅放大。 (3)阶梯圆环压电超声换能器在二阶径向共振模态下存在位移节圆,有利于在工程应用中与外部设备在节圆位置连接。 (4)阶梯圆环压电超声换能器中压电陶瓷薄圆环的内半径增大,换能器的一阶径向共振和反共振频率逐渐减小,二阶径向共振和反共振频率逐渐减小并趋于接近,此时换能器的带宽将变窄,有效机电转换系数趋于零;阶梯圆环内环外半径增大,换能器一阶径向共振和反共振频率逐渐减小,二阶径向共振和反共振频率先增大后减小。 本文所得结果对于完善径向超声换能器的设计理论和此类换能器的工程应用有一定的参考价值,有望通过换能器的径向振动实现连续超声滚动切割和焊接的应用。



2 阶梯圆环压电超声换能器的径向振动性能研究

2.1 阶梯圆环压电超声换能器径向振动等效电路和共振频率方程



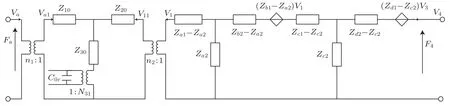

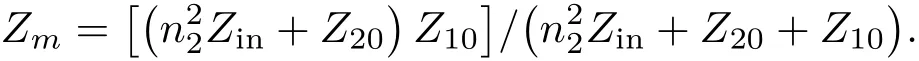


2.2 阶梯圆环压电超声换能器径向振动性能的分析


3 结论

